Файл: 2. Составление структурной схемы системы и определение передаточной функции, разомкнутой и замкнутой систем между задающим воздействием и выходом сар. Составление соответствующих дифференциальных уравнений и уравнений статики. 3.docx

Содержание

1.Описание элементов и работы системы …………………………………………………… 4

2. Составление структурной схемы системы и определение передаточной функции разомкнутой и замкнутой систем между задающим воздействием и выходом САР. Составление соответствующих дифференциальных уравнений и уравнений статики.………………………………………………………………………………………… 5

3. Построение области устойчивости в функции параметров ………………………….... 11

4. Выбор параметров регулятора из области устойчивости, построение кривой переходного процесса относительно задающего воздействия. Определение основных показателей переходного процесса …………………………………………………………………………………….. 14

6. Расчет нулей и полюсов системы ,степеней устойчивости и колебательность системы……………………………………………………………………………………… 21

7.Выбор параметров регулятора из условия минимума среднеквадратичного отклонения……………………………………………………………………………………. 23

8.Повториние результатов пункта 4……………………………………………………………………………………………….. 25

---

9. Вычисление коэффициентов ошибок по задающему, возмущающемуся воздействиям для параметров регулятора. ………………………………………………………………………………….… 27

1.Описание элементов и работы системы управления углом курса самолета



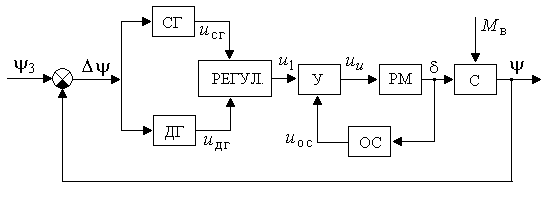
Рисунок 1 – Система автоматического управления углом курса самолета

На рисунке 1 представлена система управления углом курса самолета [1], которая представляет комплекс, состоящий из: Свободного гироскопа(СГ), дифференцирующего гироскопа(ДГ), регулятора(РЕГУЛ), усилителя(У), рулевой машины(РМ). Смена курса осуществляется при помощи штурвала (РМ), за счет сопоставления текущего курса с помощью датчиков угла (СГ и ДГ) с заданным, величина рассогласования усиливается, подается на рулевую машину, которая руль, что воздействует на объект управления. Объектом управления является корпус самолета (С).

Система работает следующим образом. Летчик, задает цель управления и наблюдает за параметрами движения самолета в пространстве (направлением, скоростью и другими). САУ сравнивает фактические значения параметров движения с заданными, проводит анализ, вырабатывает решение и, исполняя его, воздействует на командные рычаги управления (КРУ). В результате этого воздействия отклоняются органы управления (ОУ), которые изменяют силы и моменты, действующие на самолет, а соответственно и параметры движения в желаемом направлении.[3]
2. Составление структурной схемы системы и определение передаточной функции, разомкнутой и замкнутой систем между задающим воздействием и выходом САР. Составление соответствующих дифференциальных уравнений и уравнений статики.


На основании принципиальной схемы и изучения принципа работы составим функциональную схема (рисунок 2).



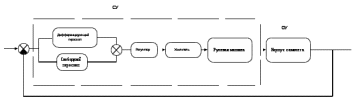
Рисунок 2 - Функциональная схема системы управления углом курса самолета

СУ- система управления;

ОУ- объект управления.

Для разработки структурной схемы необходимо получить выражения для передаточных функций элементов, входящих в систему. Для

---

этого могут быть использованы уравнения, описывающие динамику работы каждого элемента, из которых определяются передаточные функции. Для правильной реализации уравнений воспользуемся справочной литературой [2].

Дифференцирующий гироскоп: ksg = 0.9

Свободный гироскоп: kdg= 0.5

Усилитель: krm= 5.5

Рулевая машина:



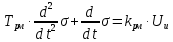
Применяя преобразование Лапласа получим







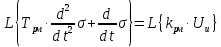
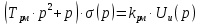
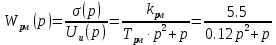
Корпус самолета:



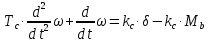
Применяя преобразование Лапласа, получим





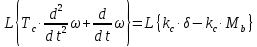
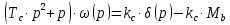
Этому уравнению соответствует структурна схема:



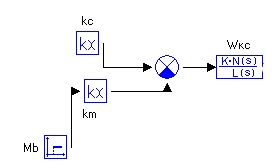
Рисунок 3- Структурная схема преобразования Лапласа

Коэффициент жесткой обратной связи: koc= 0.18

Регулятор:

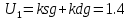
Усилитель:

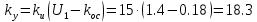
Структурная схема в пакете МВТУ будет иметь вид:

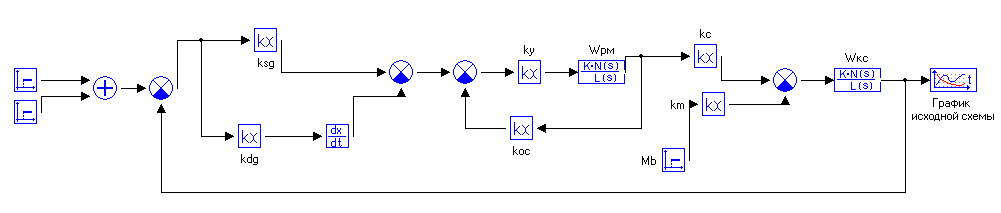
Рисунок 3- Структурная схема САУ в пакете МВТУ (Исходная схема.mrj)

Для удобства объект управления реализуем с помощью Макроблока(рисунок 4):

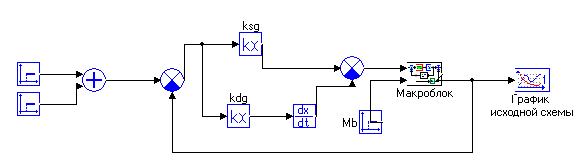
Рисунок 4- Структурная схема c макроблоком в пакете МВТУ(Макроблок и преобразованная схема .mrj)



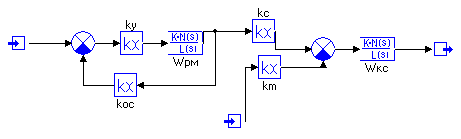
Рисунок 5- Содержимое Макроблока (Макроблок и преобразованная схема .mrj)

Преобразуем структурную схему (рисунок 6):



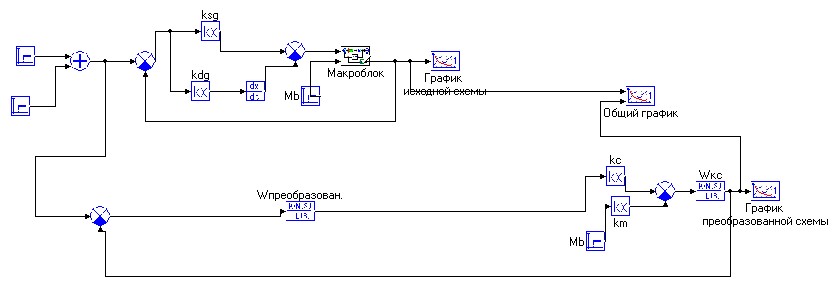
Рисунок 6- Преобразованная структурная схема(Макроблок и преобразованная схема .mrj)

---

Откроем график и убедимся в правильности преобразования (рисунок 7):



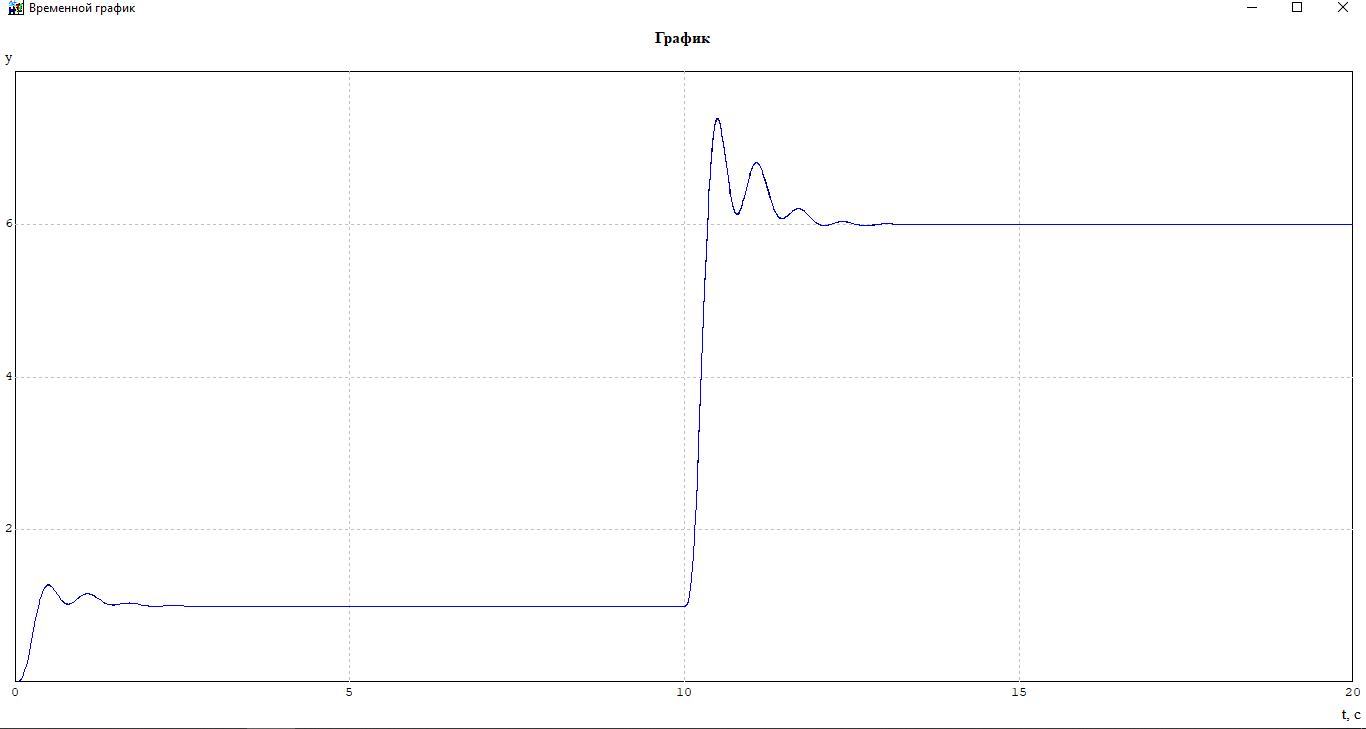
Рисунок 7- Общий график выхода схем(Макроблок и преобразованная схема .mrj)

Определим передаточные функции разомкнутой и замкнутой систем между задающим воздействием и выходом САР.



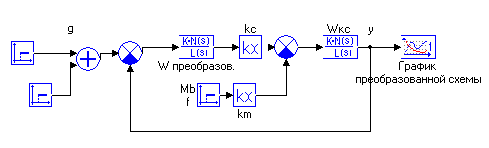
Рисунок 8- Структурная схема(Расчет ошибок .mrj)

Передаточная функция разомкнутой цепи по задающему воздействию:



Используя пакет Mathcad (Wрц.xmcd) получим:



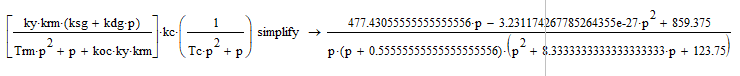
П 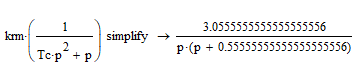ередаточная функция разомкнутой цепи по возмущающему воздействию: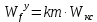



Получим:

Передаточная функция замкнутой системы по задающему воздействию:

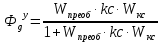
П 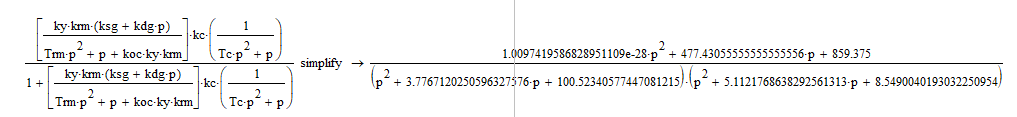олучим:

Передаточная функция замкнутой цепи по возмущающемуся воздействию:

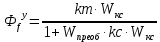
Получим:

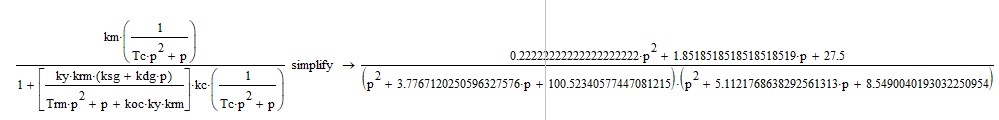
3. Построить область устойчивости в функции параметров элементов САУ указанных преподавателем.

Для того, чтобы определить, устойчива система или нет, используют критерии устойчивости. В данной работе будет использоваться критерий Михайлова. Критерий относится к группе частотных, поскольку определяет устойчивость замкнутых систем по частотным характеристикам.

Выбранными параметрами будут являться ksg , kdg- параметры включенного на вход системы регулятора.

Порядок выполнения:

Расчеты проведем с использованием среды Mathcad. (Wрц.xmcd)

1. 
   Запишем характеристическое выражение замкнутой системы:
   

2. 
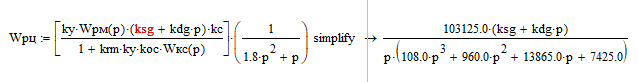
   Подставим p=j ω и выделим действительную и мнимую части
   

---

Для начала суммируем числитель и знаменатель, получим:



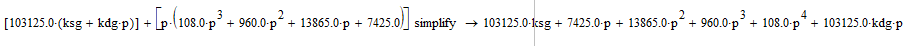
Произведем замену:



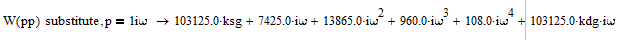
Выделим части:



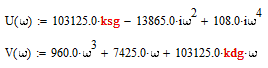
Для того чтобы система находилась на границе устойчивости необходимо, чтобы выполнялось равенство, решим систему уравнений:



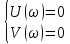
Для этого сначала сократим на ω



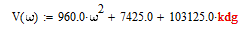
После выразим из мнимой части



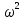
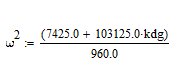
И подставим ее в действительную часть



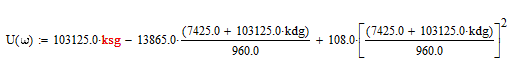
Сделаем упрощение:



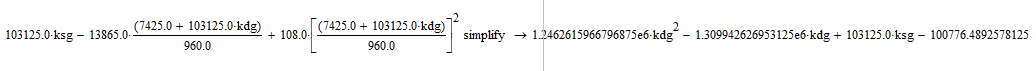
Применим kdg=x, выразим зависимость для построения графика



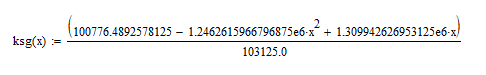
Построим график



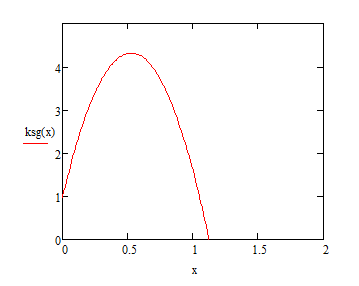
Рисунок 9-График «область устойчивости»

4. Выбор параметров регулятора из области устойчивости, построение кривой переходного процесса относительно задающего воздействия. Определение основных показателей переходного процесса (перерегулирование, время переходного процесса).

Проверим исходные данные на устойчивость системы:

kdg=0,5;ksg=0.9.

Построим кривую переходного процесса.




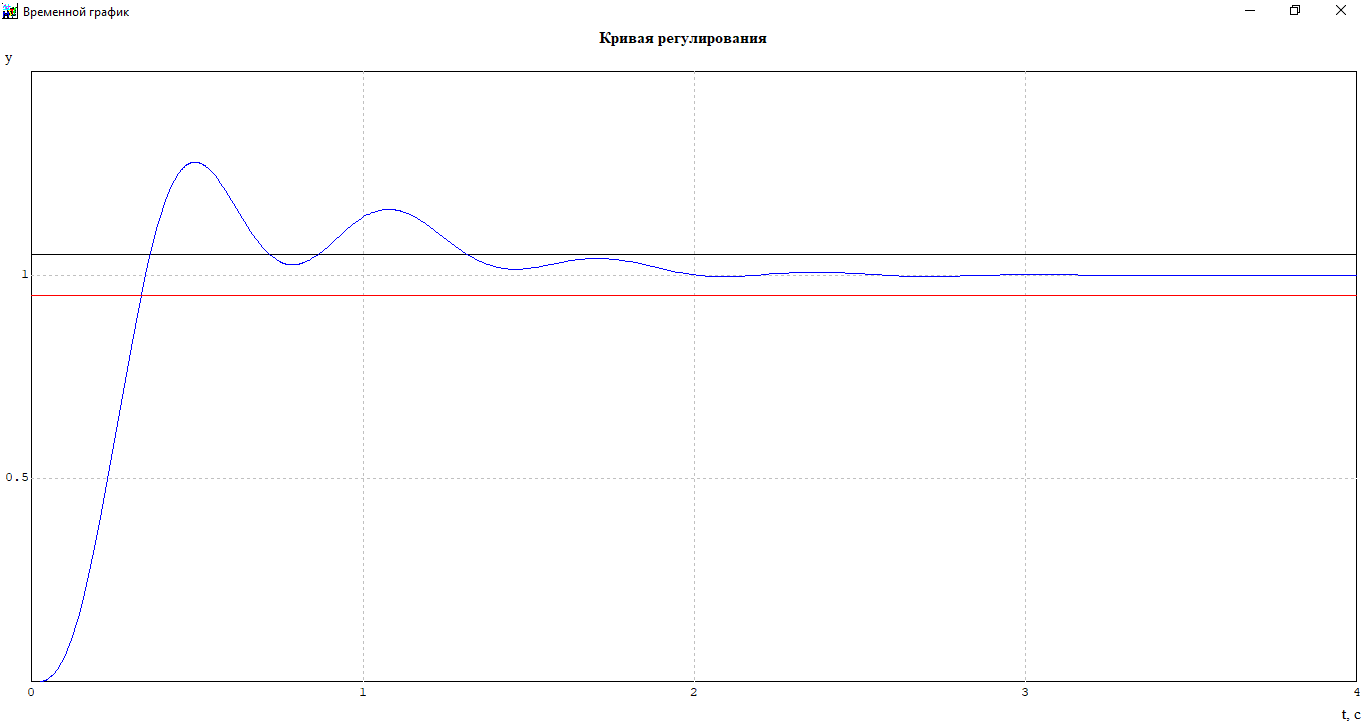
Рисунок 10-Кривая переходного процесса замкнутой системы по задающему воздействию (Макроблок и преобразованная схема.mrj)

---