Файл: Мектепте 9 сынып геометриясын зерттеп оыту технологиясы дістемелік рал.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 129
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Әртүрлі үш бұрышы бойынша үшбұрыш туралы қандай да бір тұжырым жасауға бола ма ? Болса, қандай ?
Үшбұрыштарды шешу есептерін үш түрде дәлелдеп көрсетуде зерттеуді қолайлы ұйымдастыруда оқушыларды үш топқа бөлу арқылы орындатуға болады (1-сызба).
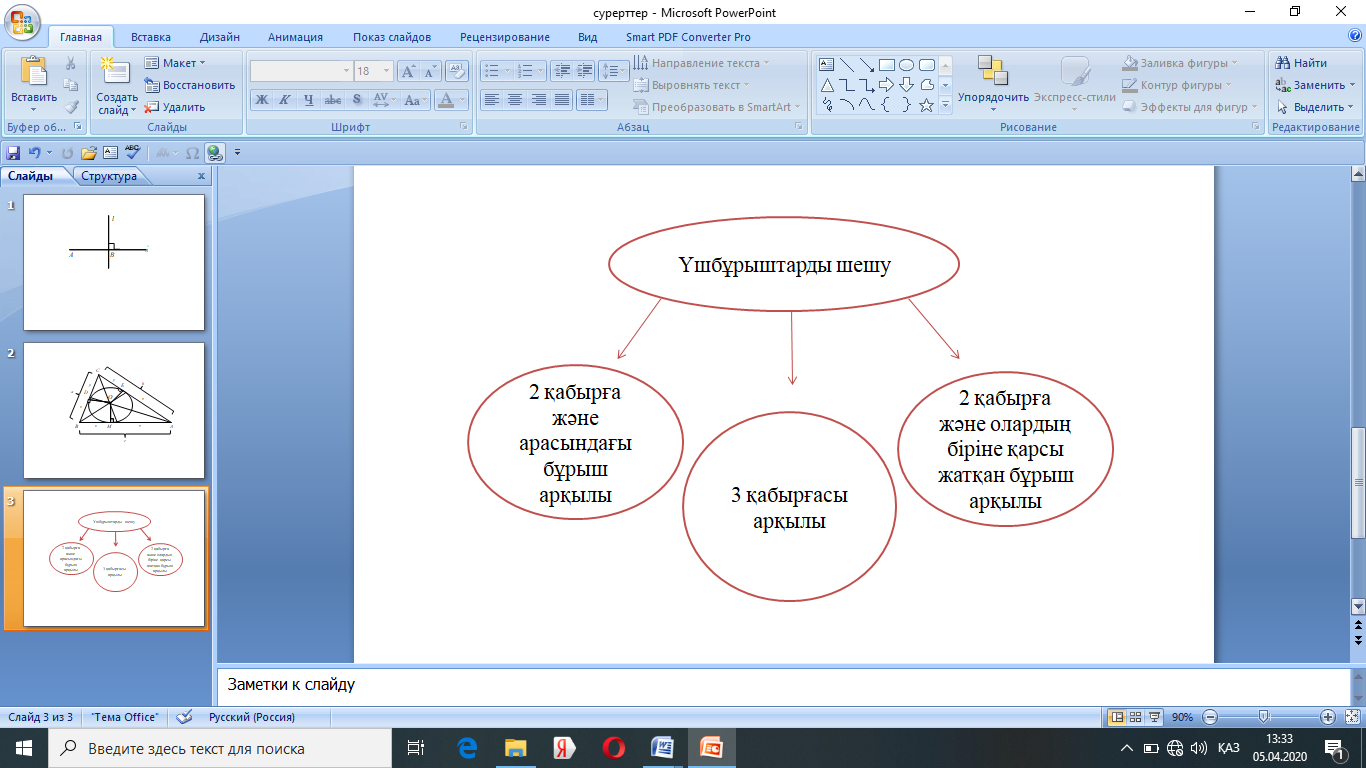
1-сызба
Бірінші топқа екі қабырғасы және олардың арасындағы бұрышы бойынша үшбұрышты шешу. Олардың зерттеу әрекетіне көмекші ретінде 2-сызбаны ұсынуға болады:
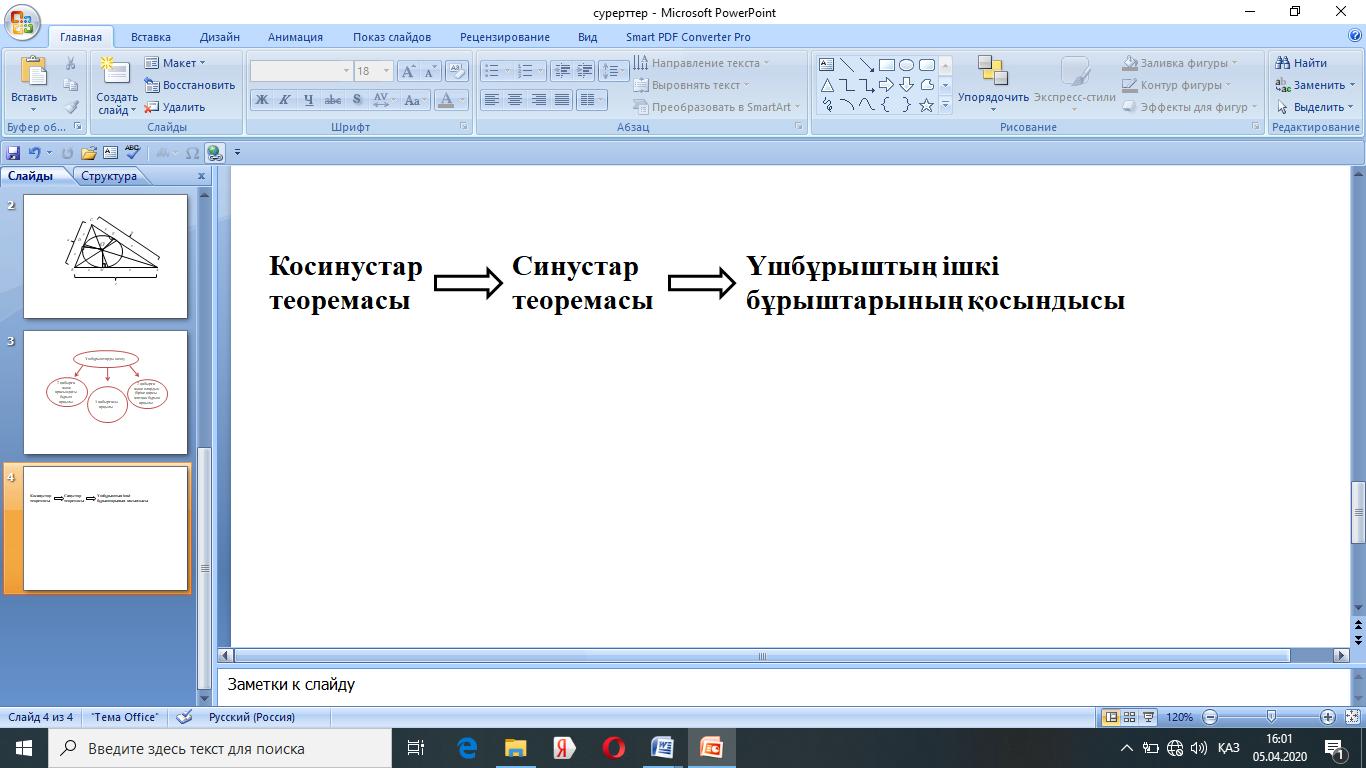
2-сызба
Көрсетілген 2-сызба бойынша олар топпен бірге зерттеуге көшеді. Яғни сызбаны пайдалана отырып,өз дәлелдеулерін ортаға салады. Топ ішіндегі алғыр оқушылар барлық ойды жинақтап, қисынға келетінін алып, болжам жасап зерттеудің нәтижесінде оны ұсынады. 3-кестеде есепті шешу кезіндегі оқушылардың тарапынан күтілетін болжам мен мұғалімнің ұсынатын болжамдарының арасындағы ұқсастықтары және айырмашылықтары салыстырылым ретінде көрсетілген.
3-кесте. Болжамдарды салыстыру кестесі («+»- ұқсайды, «-»- ұқсамайды )
| Есептің құрылымы | Оқушылардың тарапынан күтілетін болжамы | Ұқсастық | Мұғалімнің болжамы |
| Берілгені | b,cжәне 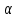 | + | b,cжәне 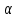 |
| Табу керек | 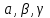 | + | 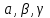 |
| Шешуі | Косинустар теоремасы бойынша, а қабырғасын табамыз: 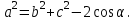 | - | а қабырғасын табу үшін косинустар теоремасын қолдану керек: 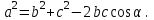 |
| Сосын синустар теоремасын қолдана отырып, 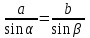 , ,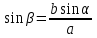 теңдігінен теңдігінен 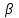 бұрышын табамыз. бұрышын табамыз. | + | Синустар теоремасын қолдана отырып, 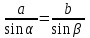 немесе немесе 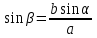 теңдігінен теңдігінен 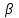 бұрышын табу керек. бұрышын табу керек. | |
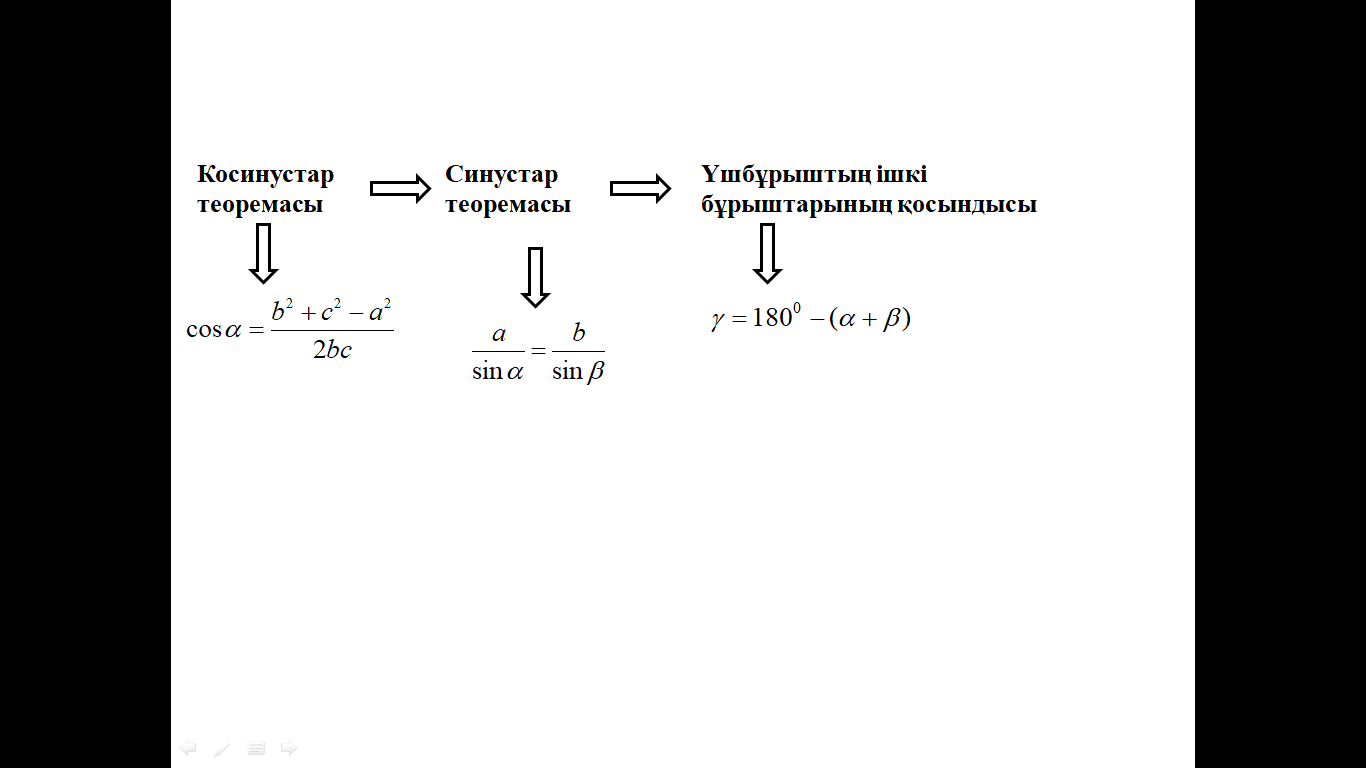
| Үшбұрыштардың бұрыштарының қосындысынан 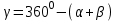 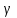 бұрышын табамыз. бұрышын табамыз. | - | Үшбұрыштардың ішкі бұрыштарының қосындысы бойынша 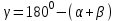 теңдігінен теңдігінен 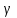 бұрышын табу керек. бұрышын табу керек. |
Егер олардың болжамы мұғалімнің ойындағыдай болмаса, онда ол болжамды жоққа шығарудың қажеті жоқ. Бұл жерде бір қуанатын жағдай ортақ ойдың жинақталып, болжам болып ұсынылуында яғни, зерттеу іс-әрекетінің талаптары: қарама-қайшылықты көру, қызығушылықтың оянуы, зерттеу болжамын жасау және оны ұсыну көрініс табады. Ал бір өкініштісі: оқушылардың формуланы жазу кезіндегі қателікті жіберуі.
Сонымен қатар, ұсынылған болжамды тексеру кезінде мынадай қателіктерді байқауға болады:
1) косинустар теоремасын жазу кезінде формуладан қате жіберу;
2) үшбұрыштардың ішкі бұрыштарының қосындысының
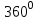 градустық өлшемде жазылуы.
градустық өлшемде жазылуы. Сол сияқты екінші және үшінші топтың болжам нәтижесін тексеру кезінде сәйкес 3 және 4 сызбаларды қолдануға болады.
3- сызба. Үш қабырғасы бойынша үшбұрышты шешу.
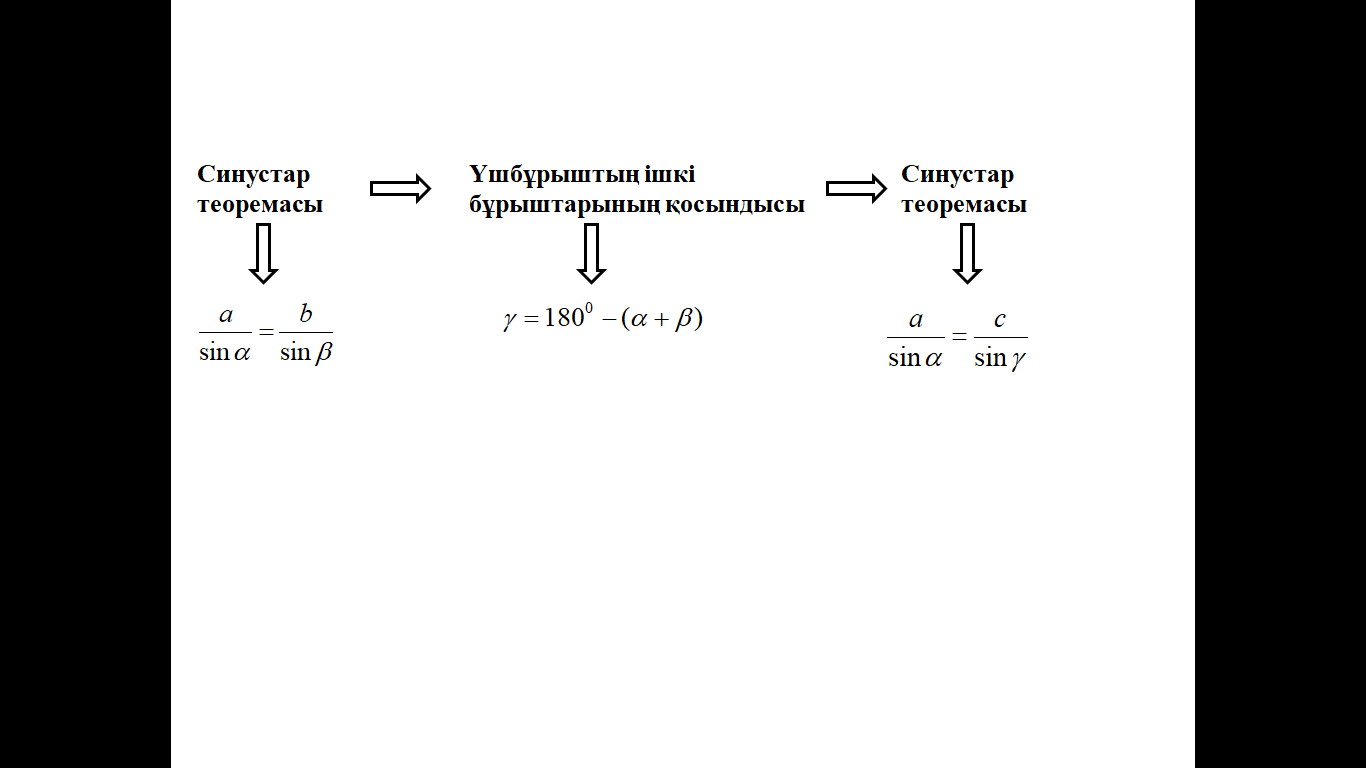
4-сызба. Екі қабырғасы және олардың біріне қарсы жатқан бұрышы бойынша үшбұрышты шешу
Әрбір топтың зерттеу болжамы әр түрлі болуы мүмкін. Жоғарыдағы сызбаларды топтың жұмыс нәтижесін тексеру кезінде қолдану өте маңызды. Себебі бұл сызбалар арқылы оқушы өзінің жадында тез сақталуы мен зерттеу қабілеттілігін шыңдай түседі. Сынып оқушылары тапсырманы әр түрлі деңгейде қабылдайтындықтан олардың орындалу үдерісінің ұзақтығы да, алынатын нәтижесі де бір-бірінен өзгеше болып келеді. Білім деңгейі орташа немесе төмен оқушыларға сызбаны дайын түрде беріп, олардың арасындағы байланысты түсіндіруді талап еткен жөн. Ал қызығушылығы жоғары, зерттеуге қабілетті оқушыларға аз ғана қолдау көрсету арқылы олардың зерттеу белсенділігін арттыруға болады.
«Косинустар теоремасы» тақырыбын қарастырғанда үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатыстар туралы еске түсіреміз. Бұл теореманы негізінен екі тәсілмен дәлелдеуді көрсетуге болады. Оқушыларға жеңіл болу үшін бірінші тәсілді көрсетелік. Мұғалім: «Бұл теореманы дәлелдеу барысында біз тікбұрыштағы сүйір бұрыштың косинусының анықтамасын, Пифагор теоремасын, қысқаша көбейту формуласын, келтіру формуласын қолданамыз»- деп бағыт береді. Оқушылар осы бағыт арқылы келесі берілетін тапсырмалармен жұмыс жасауға кіріседі. Оларға 10-сурет бойынша келесі тапсырмалар ұсынылады.
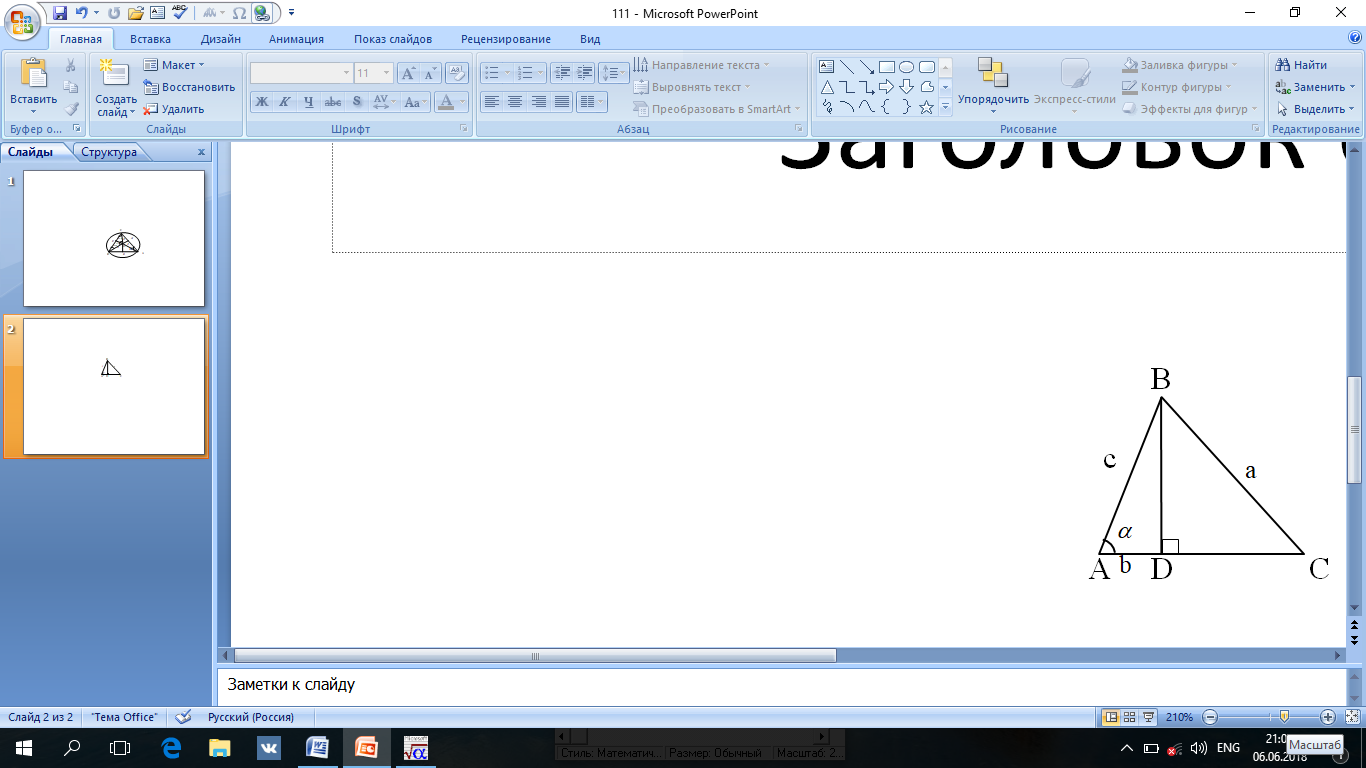
10-сурет
Мұғалім: АВС сүйірбұрышты үшбұрыш салып,
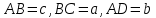 деп белгілеу енгізіп, оның В төбесінен BD биіктігін жүргізіңіздер. Пайда болған тікбұрышты ADB үшбұрышында
деп белгілеу енгізіп, оның В төбесінен BD биіктігін жүргізіңіздер. Пайда болған тікбұрышты ADB үшбұрышында 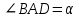 деп белгілейік.
деп белгілейік.Мұғалім: Енді осы үшбұрыштың
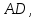
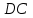 қабырғалары неге тең ?
қабырғалары неге тең ?Оқушы:
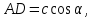
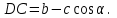
Мұғалім: Оны қалай шығардық?
Оқушы: Сүйір бұрыштың косинусының анықтамасы арқылы
Мұғалім: Келесі BD биіктігін ABD және CBD тікбұрышты үшбұрыштарынан табыңыздар.
Әрі қарай оқушылар Пифагор теоремасын қолданып
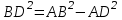 ,
,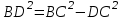 теңестіріп,
теңестіріп, 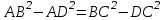 орнына берілгендерін қойып дәлелдеуді өздері орындайды.
орнына берілгендерін қойып дәлелдеуді өздері орындайды.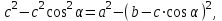 қысқаша көбейту формуласымен жақшаларды ашып
қысқаша көбейту формуласымен жақшаларды ашып 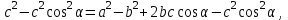 жинақтап, нәтижесінде
жинақтап, нәтижесінде 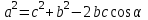 теңдігін алады. Мұғалім мұндағы,
теңдігін алады. Мұғалім мұндағы, 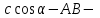 ның
ның  қабырғасындағы проекциясы екендігін айтып кеткені жөн.
қабырғасындағы проекциясы екендігін айтып кеткені жөн. Міне аз ғана қадамдардың өзінде оқушылар өздері дәлелдеуге қол жеткізді. Косинустар теоремасының дәлелдемесі оқушыларға көптеген теоремаларды еске түсіріп қолдануына жағдай жасайды. Сонымен қатар, мұндай дәлелдеуге арналған есептер оқушының жан-жақты ойлануына, шығармашылық ізденіске жол ашады. Әрине, жоғарыдағы берілген үлгі бұл тек бідің болжамымыз ғана. Ал , іс жүзінде басқаша дәлелдеуді өз ойлау қабілетімен болжам жасап ауызша ұсынатындар да бар. Оларға кері пікір айтпас бұрын, оның жіберіп тұрған қателігін оқушының өзі түсініп дұрыстауына жағдай жасау қажет. Оның қарама-қайшылықты көруі үшін оған проблемалық сұрақтар қоюға болады.
Бұл дәлелдеуден кейін оқушыларға мынадай сұрақ қойып ізденіс жұмысын жалғастыруға болады: Біз тек
АВС сүйір үшбұрыш болғанда ғана косинус теоремасын дәлелдедік. Ал бұрыштардың өлшемі доғал немесе тік болған жағдайда дәлелдеуді қалай жүзеге асыруға болады? Бұл сұраққа тез арада жауап беру қиынға соққанымен алдыңғы үлгідегідей бағыт беру арқылы олардың зерттеу жұмысына көмектесуге болады.
АВС үшбұрышының
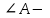 доғал болған жағдайда алынатын нәтиже:
доғал болған жағдайда алынатын нәтиже: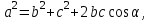
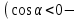 доғал бұрыш). Егер АВС үшбұрышының
доғал бұрыш). Егер АВС үшбұрышының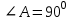 тік болса, онда
тік болса, онда 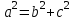 косинустар теоремасы Пифагор теоремасының жалпыланған түрі болып табылады.
косинустар теоремасы Пифагор теоремасының жалпыланған түрі болып табылады. Теореманың екінші тәсілмен дәлелденуі барысында қысқаша көбейту формуласын, векторлардың скалярлық көбейтіндісін, теңдігін қолданады. Оны математикаға ерекше қызығушылық танытқан оқушылар өз бетінше сабақтан тыс талдап, түсінулеріне болады. Қажет болған жағдайда, мұғалім оларға көмектеседі.
Ескерту. Бұрыштың косинусының табылған мәні бойынша бұрыштың түрін анықтау дағдысын оқушылардың жетік меңгергенін мұғалімнің қадағалауы керек.
Егер табылған бұрыштың косинусының мәні оң сан болса, онда берілген бұрыш сүйір бұрыш (
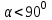 ).
).Егер табылған бұрыштың косинусының мәні теріс сан болса, онда бұрыш доғал(
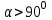 ).
).Егер табылған бұрыштың косинусының мәні нөлге тең болса, онда берілген бұрыш тік бұрыш(
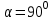 ).
).Тақырыптар бойынша оқушылар:
1)
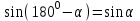 және
және 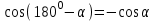 формулаларын түсініп, есте ұстаулары;
формулаларын түсініп, есте ұстаулары;2) косинустар теоремасын есте ұстап, кез келген үшбұрыштың қабырғасын, оның белгілі екі қабырғасы мен олардың арасындағы бұрышы бойынша таба алулары керек.
Синустар теоремасы. Синустар теоремасының дәлелдемесі тікбұрышты үшбұрыштың сүйір бұрышының синусының анықтамасына негізделген. Зерттеп оқыту үдерісінде осы тақырыпқа арналған тапсырмаларды орындатуда оқушыларға қиындық тумайды. Себебі олар кітапта берілген теореманыөздері дәлелдеу арқылы еш қиналмастан есепті шығара береді. Бастысы теоремада көрсетілгендей кез келген үшбұрыштың қабырғалары оларға қарсы жатқан бұрыштардың синустарына пропорционал болатындығын яғни, (12) формуланы ұмытпағаны жөн.
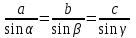 (12)
(12)Оларға мысалы мынадай тапсырманы өз беттерімен орындауға беруге болады.
-
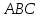 үшбұрышының ауданын
үшбұрышының ауданын 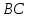 қабырғасының ұзындығы мен
қабырғасының ұзындығы мен 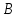 және
және 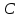 бұрыштарының мәндері арқылы өрнектеу керек.
бұрыштарының мәндері арқылы өрнектеу керек. -
Параллелограмның диагональдары m және n, ал олардың арасындағы бұрыш . Берілгендері арқылы параллелограмның қабырғаларын өрнектеңдер.
. Берілгендері арқылы параллелограмның қабырғаларын өрнектеңдер. -
Параллелограмның қабырғалары a,b және бір бұрышы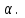 Параллелограмның диагональдарын берілгендері арқылы өрнектеңдер.
Параллелограмның диагональдарын берілгендері арқылы өрнектеңдер.