Екі жиынның қиылысуы, шеңбер, дөңгелек, жиынтық, терістеу, нүктеден түзуге дейінгі арақашықтық логикалық байланыстардың қолданысынан шығады. Факультативті немесе сыныптас тыс сабақтарда талқылауларды (силлогизм) жүзеге асыруға болады.

Қарастырылған зерттеуіміздің құрылымының математикалық сипаттамасы шеңберге жүргізілген жанаманың анықтамасымен байланысты болады. Осыдан екі әртүрлі анықтаманың тепе-теңдігі шығады: кіші теориялардың құрылуы және шеңберге жанама жүргізу.

---

Дұрыс көпбұрыштарды салу және ауданын есептеу. Сабақты бастамас бұрын мұғалім оқушыларға сұрақ қояды:

1. Көпбұрыштардың қандай түрлерін білесіңдер?

2. Дұрыс үшбұрыш, дұрыс алтыбұрыш, дұрыс төртбұрыш ұғымын бұрын естідіңіздер ме?

3. Дұрыс алтыбұрыш пен дөңес алтыбұрыштың айырмашылығы бар ма?

4. Ромбыға сырттай шеңбер сызуға бола ма?

5. Тіктөртбұрышқа іштей шеңбер сызуға бола ма?

Оқушылар осы сұрақтарға жауап беру арқылы тақырыпты анықтай отыра, іштей және сырттай сызылған шеңберлердің центрлері сәйкес төртбұрыштың диагональдарының қиылысу нүктесінде жататындығын түсінеді.

Нұсқаулық. Шеңберге іштей сызылған дұрыс көпбұрышты салу үшін, оның центрлік бұрышын салу жеткілікті.

Осы нұсқаулықты және анықтаманы қолдана отырып, дұрыс алтыбұрыштың ондай бұрышы 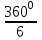-қа тең болатындығын қорытып шығарады. Мұғалім бағыт беру беру арқылы оқушыларды сурет салуға итермелейді, бұл іс-әрекет оқушылардың уәждемелік қызметін арттыра түседі.

Мұғалім: дұрыс алтыбұрышты салу үшін оның бір төбесін А₁ шеңбер бойынан қалауымызша алайық. Ол нүктеден, центріретінде, шенбердің радиусына тең радиуспен белгі салып, А₂ төбесін шығарып аламыз.

Бұдан қейін оқушылар қалған төрт төбені яғни, А₁, А₄, А₅, А₆ төбелерді соған ұқсас түрде салып, оларды кесінділермен қосады. Осылайша, 7-сурет пайда болады.



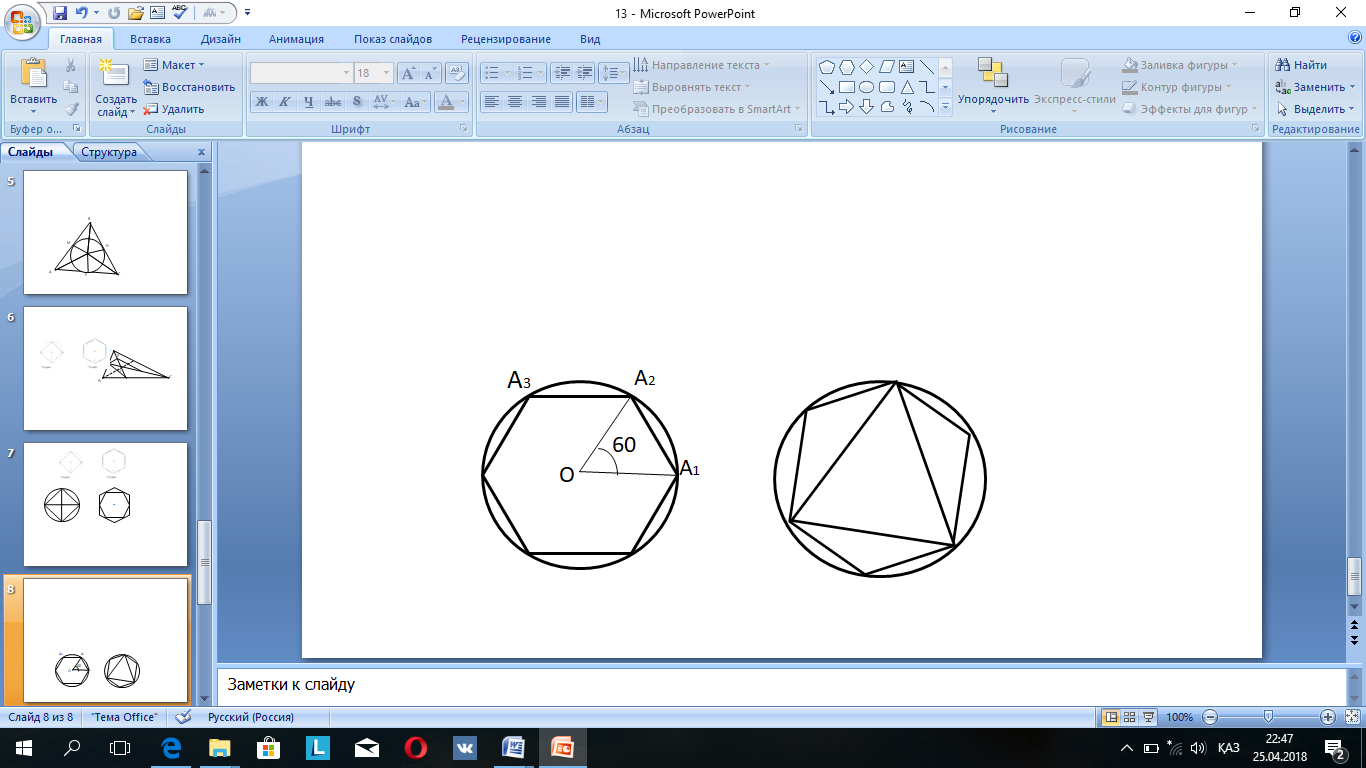
7-сурет 8-сурет

Мұғалім: Оқушылар шеңберге іштей сызылған дұрыс алты бұрышты пайдаланып, шеңберге іштей сызылған дұрыс үшбұрышты сала аласыздар ма?

Оқушы: Я, шеңберге іштей сызылған дұрыс үшбұрышты салу үшін шеңберге іштей сызылған дұрыс алты бұрыштың төбелерін бір-бірден аттап қосу жеткілікті (8-суретті көрсетеді).

Мұғалім: Жарайсыздар, енді шеңберге іштей сызылған дұрыс төртбұрышты яғни квадратты қалай салуға болады?

Оқушы: Шеңберге іштей сызылған квадратты салу үшін шеңбердің центрі арқылы перпендикуляр түзулер жүргіземіз. Олар шеңберді қвадраттың төбелерінде қиып өтеді (9-сурет).



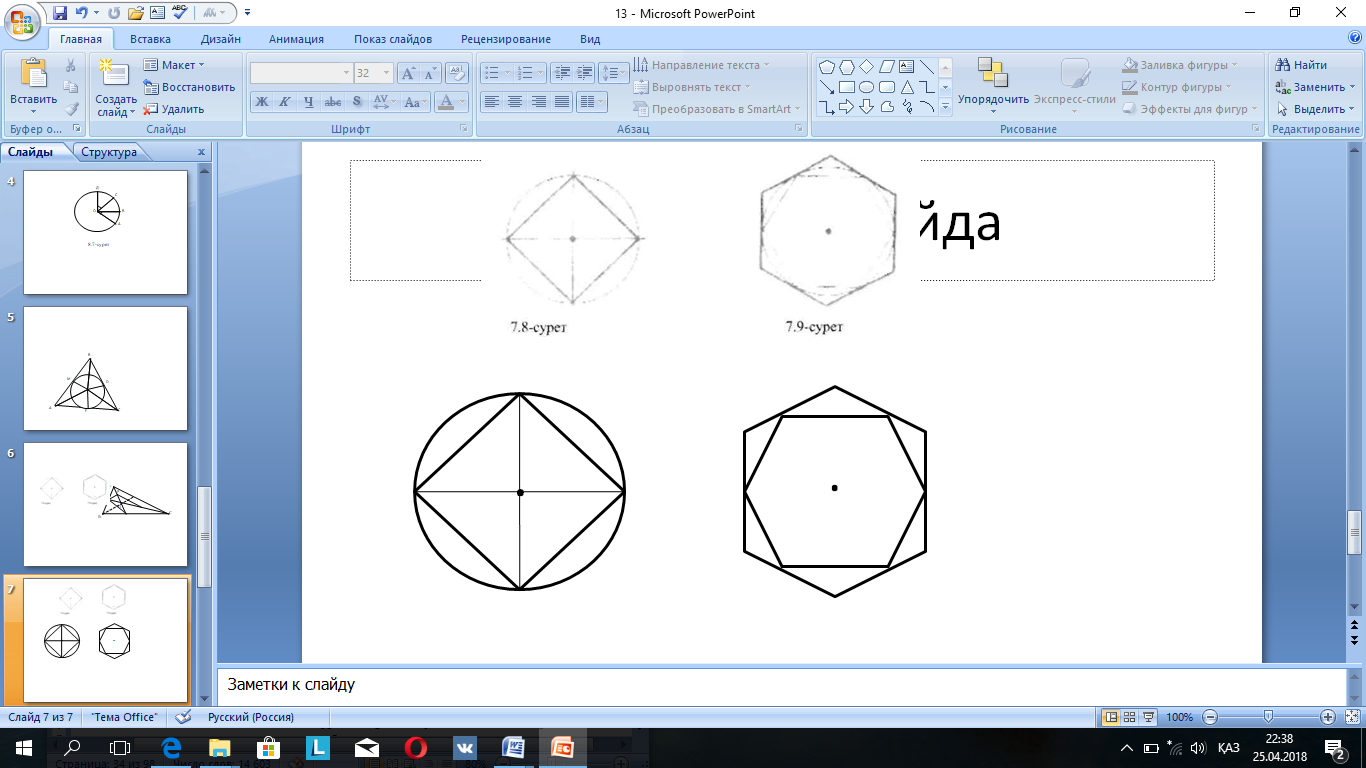
9-сурет

_{Жоғарыдағы сұрақтар оңай болғандықтан, шеңберге іштей және сырттай сызылған дұрыс көпбұрыштар анықтамасын оқушыларға саналы меңгертуге жол ашылады, тіпті төмендегі теореманы дәлелдеу қиын болмай қалады. Кез келген көпбұрышқа іштей және сырттай шеңбер сызуға болады және іштей, сырттай сызылған шеңберлердің центрлері беттеседі [17].}

---

<sub>Іштей сызылған дұрыс n бұрышты көпбұрыштың периметрінің қасиеті: берілген шеңберге іштей сызылған барлық n бұрышты көпбұрыштардың ішінде периметрі ең үлкен болатыны n бұрышты дұрыс көпбұрыш.

Бұл теореманы дәлелдеу үшін төмендегі лемманы пайдалануға болады.

Лемма. Бір қабырғасы және оған қарсы жатқан бұрышы тең болатын тең емес екі үшбұрыштың қайсысының ауданы үлкен болса, соның периметрі үлкен болады.

Теореманың дәлелдеуін оқушылардан талап ету қажет емес. Теорема дәлелдеуіне қолданылатын лемманы дәлелдеусіз-ақ пайдалануға болады. Осындай жұмыстардың нәтижесінде оқушылар:</sub>

1) дұрыс көпбұрыш анықтамасын;

2) шеңберге іштей және сырттай дұрыс үшбұрышты, дұрыс төртбұрышты, дұрыс алтыбұрышты циркуль мен сызғышты пайдаланып салуды;

<sub>3) дұрыс көпбұрышқа сырттай;

4) дұрыс көпбұрышқа іштей шеңбер сызуға болатынын;

5) дұрыс көпбұрышқа іштей сызылған шеңбер көпбұрыштың қабырғаларын олардың орталарында жанайтынын;

6) дұрыс көпбұрышқа сырттай және іштей сызылған шеңберлердің центрі ортақ бір нүкте екенін;

7) дұрыс көпбұрыштың центрін табуды;

8) шеңберге іштей сызылған n бұрышты көпбұрыштардың ішінде дұрыс көпбұрыштың периметрі ең үлкен болатынын меңгеруі маңызды.</sub>

Көпбұрыштардың ауданын есептеу кезінде Л.Н. Толстойдың «Много ли человеку нужно» атты әңгімесінен: «Бір күннің ішінде жаяу жүргінші ең тиімді жолмен қаншалықты үлкен жерді өтіп шыға алады?»- деген сұраққа жауап ізделінеді. Осы есептің математикалық моделін құрастыралық.

Есеп шарттарына уақытты, жылдамдықты тұрақты деп есептейміз, сонда адамның жолы да тұрақты, яғни жаяу жүргіншілер жүретін геометриялық фигураның периметрі да тұрақты болады. Сондықтан, осы периметрде қандай фигураның ауданы үлкен екенін табу керек.

Оқушыларға түсінікті болу үшін мұғалім ауданы ең үлкен фигураны табу керектігін ұсынады. Есепті шешу үшін алдымен теңқабырғалы үшбұрышты қарастыралық. Осы арқылы оқушылар бұрынғы ақпаратты еске түсіреді.

.

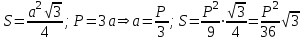Яғни, теңқабырғалы үшбұрыштың ауданын оның периметрімен өрнектеу арқылы (7) теңдікті алады:

---

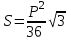
(7)

Қабырғасы х-ке тең квадратты қарастырайық:



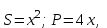
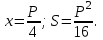
Осыдан, квадраттың ауданын оның периметрі бойынша өрнектеп, (8) теңдікті алады:

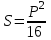(8)

Қабырғасы х-ке тең ромбының ауданы (9) теңдік болады:

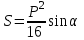(9)

Дұрыс алтыбұрыш қабырғасы b болсын. Онда оқушылар төмендегідей есепті шығара алады:



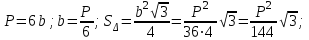
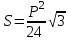(10)

Квадраттың қабырғасы m , тіктөртбұрыштың қабырғасы a,b болсын. Квадраттың ауданы тіктөртбұрыштың ауданына қарағанда үлкен болатындығын дәлелдейік, яғни 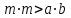осы теңдікті оқушыларға дәлелдету қажет. Ол үшін бастапқы периметрлері бірдей деген шартты пайдаланады:

.

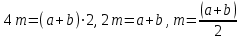Квадраттың ауданының формуласына сәйкес m-ді қойып, нәтижесінде (11) теңдікті алады:



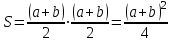
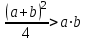(11)

(11) теңдіктен 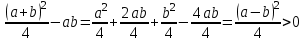алынады. Бұл дұрыс теңдік, себебі санның квадраты оң сан болады.

Демек периметрлері бірдей болған жағдайда, тіктөртбұрыштың ауданы квадраттың ауданынан кіші болады екен.

Алынған нәтижелерді салыстыратын болсақ, ромбының ауданының формуласында 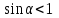болғандықтан, ромбының ауданы квадраттың ауданынан кіші.

Теңқабырғалы үшбұрыш ауданы дұрыс алтыбұрыштың ауданынан кіші.

Келесі кезекте, алтыбұрыш пен квадраттың ауданын салыстырайық.

Екі ауданның формуласынан алдыңғы коэффициенттерін аламыз, 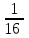және 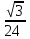. Екі бөлшектің ортақ бөлімі 48 саны болады, яғни 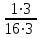және .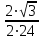

Осыдан, 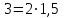екінші бөлшекте

---

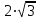. Демек, 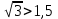. Яғни алтыбұрыштың ауданы үлкен.

Зерттеу нәтижесінде алтыбұрыштың ауданы бәрінен үлкен екендігіне оқушылар көз жеткізеді. Осы секілді есептерді сабақтың үстінде шығарту арқылы олардың зерттеу қабілетінің дамуына ерекше әсер қалдыруға болады.

Үй тапсырмасына оқушылардың ізденіс белсенділігін күшейту үшін мына екі тапсырманы беруге кеңес береміз:

1) Қабырғасының ұзындығы а см болатын 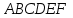дұрыс алтыбұрышының 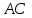және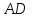 диагональдарының ұзындығын қалай анықтауға болады?

2) Егер дұрыс көпбұрыштың ішкі бұрыштары қосындысы оның сыртқы бұрыштары қосындысына тең болса немесе оның сыртқы бұрыштары қосындысынан 2,5 есе үлкен болса көпбұрыш қабырғаларының санын анықта.

Синустар және косинустар теоремаларын үшбұрыштарды шешуде және қолданбалы есептерде қолдану. Үшбұрышты шешу үшін косинустар теоремасы, синустар теоремасы қарастырылады.Үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатыстар туралы косинустар теоремасы дәлелдесе, үшбұрыштың бұрыштарының синустары оларға қарсы жатқан қабырғаларға пропорционал.

Алдымен оқушылардың назарын үшбұрыштардың негізгі алты элементіне (үш қабырғасы мен үш бұрышына) аударту керек. Ондағы мақсат үшбұрыштарды шешу дегеніміз оның барлық қабырғалары мен барлық бұрыштарын анықтау екендігін көрсету еді.

Оқушылардың зерттеу белсенділігін арттыру үшін мына сұрақтарды ұсынуға болады:

1. Үшбұрыштарды шешу дегенді қалай түсінесіңдер?

Жауабы:

1) үшбұрыштарды шешу дегеніміз оның барлық қабырғалары мен барлық бұрыштарын анықтау;

2) үшбұрыштың белгісіз элементтерін табу.

2. Үшбұрыштың екі қабырғасы және олардың арасындағы бұрышы дегенді бұрын қандай тақырыптардан еститін едіңдер ?

Жауабы:

1) үшбұрыштар теңдігінің белгісі;

2) үшбұрыштардың ұқсастығы.

3. Үшбұрыштың берілген екі қабырғасы және олардың арасындағы бұрышы бойынша косинустар теоремасын қолданбай-ақ үшінші қабырғасын табуға бола ма ? Қалай ойлайсыңдар ?

2. Берілген екі бұрышы және бір қабырғасы бойынша үшбұрыштың қабырғасын қалай анықтауға болады ?

---

Смотрите также файлы

• С ocacola classic (классическая кола).docx

• Курс на ускорение развития общества середины 1980х годов.docx

• Ваучерная приватизация особая форма безвозмездной приватизации государственной собственности по принципу "дележки" государственной собственности, предназначенной для приватизации, между всеми трудящимися.docx

• Существование общества невозможно без постоянного производства материальных благ и услуг.docx

• Благодаря своей относительной простоте применения, быстроте соединения различных материалов сварка находит широкое применение.docx