Добавлен: 02.02.2019
Просмотров: 13139
Скачиваний: 101
.
(5.6)
Қандай
да бір бет арқылы
бірлік
уақытта толқын тасымалдайтын энергия
осы бет арқылы өтетін энергия
ағыны
деп аталады:
.
Беттің
әртүрлі нүктесінде энергия ағыны әртүрлі
болуы мүмкін, сондықтан энергия ағынының
тығыздығы деген ұғым енгізіледі. Бұл
энергия тасымалының бағытына перпендикуляр
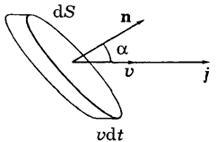бағытталған
бірлік аудан арқылы өтетін энергия
ағыны:
.
(5.7)
Гармоникалық толқындар үшін толқынның энергия тасымалының жылдамдығы фазалық
5.1
cурет жылдамдыққа тең
.
Табанының ауданы
және
ұзындығы
тең
қиық цилиндр ішінде жинақталған энергия
(5.1
суретті қара)
.
Бұл
формуланы (5.7)-ге қойып, энергия ағынының
тығыздығы үшін формуланы аламыз:
.
Ағынның
тығыздығын және оның бағытын анықтау
үшін
Умов
векторын енгізеді:
,
(5.8)
мұндағы
-
модулі толқынның фазалық жылдамдығына
тең берілген нүктеде толқынға нормаль
жылдамдық векторы.
Энергия ағынының тығыздығының уақыт бойынша орташа мәні толқынның қарқындылығы деп аталады:
.
6 Дәріс. Электрмагниттік толқындар
Дәрістің мақсаты:
- электрмагниттік толқынның дифференциалдық теңдеуін жазу;
- электрмагниттік толқынның энергиясы, Пойнтинг векторы ұғымдарын енгізу.
Максвелл теориясы бойынша (2,3), айнымалы магнит өрісі айнымалы электр өрісін тудырады және керісінше. Егер кеңістіктің белгілі бір нүктесінде құйынды электр өрісін тудырсақ, онда қоршаған ортада электр және магнит өрістерінің өзара айналымы пайда болады, яғни электрмагниттік өріс уақыт пен кеңістік бойынша таралады. Бұл процесс периодты және электрмагниттік толқын деп аталады.
6.1 Электрмагниттік толқынның дифференциалдық теңдеуі
Максвелл
теориясына сәйкес, еркін электр
зарядтарынан да
және
макроскопиялық
токтардан
да қашықта орналасқан электромагниттік
толқындар үшін (1.1-кестедегі 1-4) теңдеулер
мына түрде жазылады
,
,
,
.
и
байланысын
ескеріп, жазатын болсақ
,
,
,
,
(6.1)
мұндағы
және
-
ортаның
тұрақты өтімділіктері.
Жазық
толқын х
осі бойымен таралса,
мен
векторлары
пен
осьтеріне
тәуелді болмайды. Бұл кезде (6.1) теңдеуінен
екі тәуелсіз теңдеулер тобын аламыз:
и
.
(6.2)
(6.2) теңдеуді (5.3) формуламен салыстырамыз, онда (6.2) электрмагниттік толқынның толқындық теңдеулері болып табылады.
Бұл теңдеулердің шешімдері
и
.
(6.3)
(6.2)-(6.3) теңдеулерден электрмагниттік толқынның негізгі қасиеттері шығады.
6.1.1
(6.1) теңдеуден
пен
кеңістік
пен уақытқа тәуелді емес екені шығады.
Сондықтан жазық толқынның айнымалы
өрісі үшін
и
мен
векторлары
толқынның таралу бағытына перпендикуляр,
яғни электрмагниттік толқындар көлденең
толқындар
болып табылады.
6.1.2 (6.2) пен (5.3) теңдеулерді салыстырсақ, электрмагниттік толқындардың фазалық жылдамдығы ортаның қасиеттеріне тәуелді
.
(6.4)
6.1.3
(6.2) теңдеуден шығатыны:
и
векторлары
өзара перпендикуляр,
,
,
векторлары оң бұрандалы жүйені құрайды
(6.1-суретті қара).
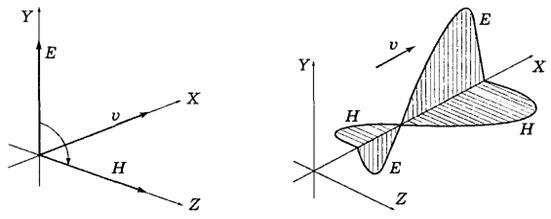
6.1 сурет 6.2 сурет
6.1.4
(6.3) теңдеудегі бастапқы фазалар тең
және
.
Сондықтан
и
векторларының
тербелісі (6.2 суретті қара) синфазалы
(бірдей фазада) және олардың лездік мәні өзара байланысты:
.
(6.5)
6.1.5
Электрмагниттік өрістің әрбір нүктесінде
и
векторлары
бірдей жиілікпен гармоникалық тербеледі.
Сондықтан электрмагниттік толқын
монохроматты
болып табылады.
6.2 Электрмагниттік толқын энергиясы. Пойнтинг векторы
Энергия тасымалы электрмагниттік толқынмен байланысты. Изотропты ортада электрмагниттік өріс энергиясының тығыздығы электр және магнит өрістерінің энергия тығыздықтарының суммасына тең:
.
және
векторларының
байланысын ескерсек, электрмагниттік
толқынның энергиясының көлемдік
тығыздығы
,
(6.6)
мұндағы
-
толқынның жылдамдығы (6.4).
(6.6)
өрнекті жылдамдыққа
көбейтсек,
энергия ағыны тығыздығын аламыз:
.
(6.7)
мен
векторлары
өзара перпендикуляр және бағыттары оң
бұрандалы жүйе таралу бағытына сәйкес
(6.1-сурет), сондықтан (6.7) теңдеу мына
түрде жазылады.
.
(6.8)
векторы
Пойнтинг
векторы деп
аталады. ол электрмагниттік толқынның
таралу бағытымен бағыттас, ал модулі
электрмагниттік толқынның таралу
бағытына перпендикуляр бірлік аудан
арқылы тасымалданатын энергияға тең.
Гармоникалық электрмагниттік қума толқын үшін энергия ағынының тығыздығы
.
Толқын
интенсивтілігі
энергия
ағынының тығыздығының орташа мәніне
тең:
,
(6.9)
өйткені косинустың квадратының орташа мәні ½-ге тең.
6.3 Электрмагниттік толқынның сәуле шығаруы
Қоршаған ортада қайсыбір жүйенің электрмагниттік толқын тудыру процессі толқындардың сәуле шығаруы деп аталады, ал аталған жүйе сәуле шығаратын жүйе деп аталады.
Сәуле
шығаратын қарапайым жүйе электрлік
диполь болып табылады; оның
моменті
уақыт бойынша өзгереді
.
(6.10)
Біртекті
изотропты ортада толқынның дипольдан
қашықтықта
орналасқан нүктелерге жету уақыты
бірдей, тербеліс фазасы да бірдей. Толқын
амплитудасы дипольдан алыстаған сайын
кемиді
,
мұндағы
-
дипольдің осі мен нүктенің радиус
векторы
арасындағы
бұрыш (6.3 суретті қара).
6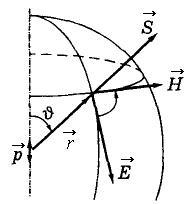
.3
сурет 6.4 сурет
Суреттен
көрініп тұрғандай,
векторы
толқындық беттің әр нүктесінде меридианға
жанама бойымен бағытталған, ал
векторы
параллельге жанама бойымен бағытталған,
Пойнтинг
векторы
мен
векторларына
перпендикуляр бағытталған. Толқынның
интенсивтілігі
.
(6.11)
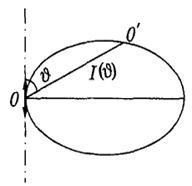
Бұл
тәуелділікті дипольдың сәуле шығару
диаграммасынан көреміз (6.4-суретке
қараңыз). (6.11) теңдеу мен келтірілген
диаграммадан байқайтынымыз, диполь
экваторлық жазықтықта
максималды
сәуле шығарады, ал
ось
бойында сәуле шығармайды. Сәуле шығару
қуаты тербеліс жиілігіне тәуелді,
-не
тура пропорционал.
Жекелеген оптикалық есептерді шешу кезінде атомды сәуле шығаратын диполь деп қарастырады, мұнда электрон ядроның айналасында тербеліс жасайды деп есептелінеді.
7 Дәріс. Толқындық оптика
Дәрістің мақсаты:
- интерференция құбылысын оқып үйрену;
- дифракция құбылысымен танысу.
7.1 Жарық толқыны
Электрмагниттік толқынның вакуумдегі жылдамдығы
.
Бұл жарық жылдамдығымен дәл келеді. Осыны негізге ала отырып, жарық электрмагниттік толқын деген қорытынды жасаймыз. Электрмагниттік толқынның барлық қасиеттері жарыққа да сәйкес келеді.
(7.1)
n шамасы сыну көрсеткіші деп аталады. Ортадағы электрмагниттік толқын жылдамдығы
.
(7.2)
Мөлдір
заттар үшін
,
сондықтан
.
(7.3)
Жарықтың ортадағы толқын ұзындығы
,
мұндағы
-
вакуумдегі толқын ұзындығы.
Жарықтың
I
интенсивтілігі
Пойтинг
векторымен
анықталады, сондықтан
,
(7.4)
яғни жарықтың I интенсивтілігі ортаның сыну көрсеткішіне және жарық толқыны амплитудасының квадратына тура пропорционал.
Жарықты сипаттау үшін электр өрісінің кернеулік векторы қолданылады, себебі жарық физиологиялық, химиялық, фотохимиялық әсері электр өрісінің кернеулік векторының тербелісінен туындайды.
7.2 Жарықтың интерференциясы. Когеренттілік
Жарықтың интерференциясы дегеніміз – жарық толқындары қабаттасқанда кеңістіктің белгілі бір нүктесінде толқындардың күшеюі және келесі бір нүктелерінде толқындардың әлсіреу құбылысы.
Интерференция құбылысын бақылау үшін қажетті шарт – толқындардың когерентті болуы.
Когеренттілік дегеніміз – бірнеше тербелмелі немесе толқындық процесстердің кеңістік пен уақыт бойынша үйлесімді өтуі.
Бұл шартты монохроматты толқын қанағаттандырады.Монохроматты тодқындар белгілі бірдей жиіліктегі амплитудасы тұрақты толқындар. Реалды жарық көзінен монохроматты жарық алу мүмкін емес, себебі жеке атомдардың сәуле шығаруы бір-біріне тәуелсіз және олардың фазаларының айырымы кездейсоқ шама.
Кеңістіктің
берілген нүктесінде екі тербелістің
фазалар айырымы уақыт өтуімен өзгермесе,
уақыт бойынша когеренттілік деп аталады.
Бастапқы фаза кездейсоқ өзгерістер
әсерінен бастапқы мәнінен
шамасына
өзгеше мән қабылдайтын уақыт когеренттілік
уақыты деп аталады.
Екі
тербелістің фазалар айырымы толқын
бетінің әртүрлі нүктесінде тұрақты
болатын үйлесімділік кеңістік бойынша
когеренттілік деп аталады. Фазалар
айырымының мәні
шамасына
жететін арақашықтық когеренттілік
ұзындығы деп аталады.
Сонымен толқындардың интерференциясының байқалу шарты төмендегідей:
1) жиіліктері бірдей;
2) фаза айырымы уақыт бойынша тұрақты.
Реалды жарық көзінен когерентті толқындарды алудың бір ғана жолы бар. Ол үшін бір жарық толқынын оптикалық жүйе арқылы екі бөлікке бөлеміз, сонда олардың оптикалық жолы әртүрлі болады; осыдан кейін екеуін қайтадан қосамыз.
Жарық
толқындары қабаттасқанда суперпозиция
принципі орындалады, яғни кеңістіктің
әрбір нүктесіндегі қорытқы кернеулік
.
Егер
мен
векторлары
бір бағытта тербелсе, векторлық диаграмма
(4.2 суретті қара) әдісін қолданып, екі
векторды қосамыз. (4.3) пен (7.4) өрнектерді
ескерсек, қорытқы толқынның интенсивтілігі
.
(7.5)
Кеңістіктің
болатын
нүктелерінде, интенсивтілік
,
ал
болатын
нүктелерінде, интенсивтілік
.
Интерференциялық көріністі бақылау нүктесінде тербелістің фазалар айырымы
,
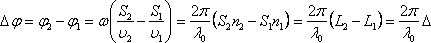мұндағы
-
екі когерентті толқынның жарық көзінен
интерференциялық көріністі бақылау
нүктесіне дейінгі жүретін жолы;
мен
-
сыну көрсеткіштері
мен
болатын
орталардағы толқындардың фазалық
жылдамдығы;
-
вакуумдегі толқын ұзындығы.
Жарық
толқыны жолының
геометриялық
ұзындығының ортаның сыну көрсеткішіне
көбейтіндісі жолдың оптикалық
ұзындығы
деп аталады, ал
оптикалық
жолдар айырмасы деп аталады.
Фазалар айырымы мен оптикалық жолдар айырмасы өзара байланысты
.
(7.6)
(7.5) өрнектен қорытқы тербеліс интенсивтіліктерінің максимум және минимум шарттары шығады:
егер
,
мұндағы
және
егер
,
мұндағы
және
.
Жарық толқындары қабаттасқанда, оптикалық жолдар айырмасы жарты толқын ұзындығының жұп сандарына тең болатын нүктелерде олар бірін-бірі күшейтеді; ал тақ сандарына тең болатын нүктелерде әлсіретеді.
7.3 Жарық дифракциясы
Ньютон теориясы бойынша жарық біртекті ортада бірқалыпты түзу сызық бойымен таралады. Көптеген тәжірибелер нәтижесінде бұл қағиданың универсалды емес екені дәлелденді. Жарықтың тар саңылаулардан, яғни оптикалық біртексіз ортадан өтуі кезінде, экранда жарықтың интерференциялық максимум немесе минимум жүйесі бақыланды.
Жарық дифракциясы дегеніміз – жарықтың өзінің толқын ұзындығымен шамалас тосқауылды орағытып өту құбылысы. Дифракциялық көрініс когерентті толқындардың қосылу нәтижесінде пайда болады.
Дифракцияның екі түрі бар: Фраунгофер дифракциясы және Френель дифракциясы. Фраунгофер дифракциясы кезінде тосқауылға жазық толқын (параллель сәулелер) келіп түседі. Френель дифракциясы кезінде тосқауылға сфералық толқындар түседі.
Жарықтың
бір өлшемді дифракциялық тордан өтуі
кезіндегі дифракцисын қарастырайық.
Дифракциялық тор дегеніміз – ені бірдей
саңылаулар мен мөлдір емес ортаның
кезектесіп орналасқан жүйесі. Тордың
саңылауларының ені a-ға, мөлдір емес
аралықтар b-ға тең.
шамасы
дифракциялық тор тұрақтысы немесе
периоды деп аталады. Монохроматты жазық
толқын дифракциялық торға нормаль
бойымен түссін. Тордан кейін қойылған
жинағыш линза жарықты өзінің фокус
жазықтығында жинайды. Саңылаудан өткен
жарық дифракция салдарынан бастапқы
бағытынан әр түрлі бұрышқа шашырайды.
Толқындар фазалар айырымына байланысты
бірін-бірі жояды немесе күшейтеді.
Саңылаулар бір-бірінен бірдей қашықтықта
жатқандықтан, көршілес екі саңылаудан
шыққан сәулелердің оптикалық жол
айырымдар
бағыты
бірдей болады
.
(7.7)
Жарық интенсивтілігінің негізгі минимумдары бақыланатын бағыттар
(
)
(7.8)
шартынан анықталады.
Сонымен қатар әртүрлі саңылаудан келіп түскен сәлелер бірін-бірі жоятын болса, қосымша минимудар пайда болады
(
)
(7.9)
Негізгі максимумдар
(
)
(7.10)
шартынан анықталады. Сонымен саңылаулар саны N болса, екі негізгі максимумның арасына N-1 қосымша минимумдар орналасады. Негізгі максимумдар саны дифракциялық тор периодының толқын ұзындығына қатынасынан анықталады
.
(7.11)
7.3 Жарық поляризациясы
Жарық
көлденең электрмагниттік толқын болып
табылады. Жарық толқынының
векторы
мүмкін болатын барлық бағытта тербелетін
болса, мұндай жарық табиғи жарық деп
аталады. Мысал ретінде күн сәулесін,
электр шамының жарығын келтіруге болады.
Қандай да бір жағдай жасалып, жарық векторы бір бағытта ғана тербелетін болса, ол поляризацияланған жарық деп аталады. Поляризатор көмегімен табиғи жарықтан поляризацияланған жарықты алуға болады. Жарық поляризациясын сипаттау үшін поляризацилану дәрежесі деген шама енгізейік
,
(7.12)
мұндағы
,
-
жарық интенсивтілігінің максимум және
минимум мәндері.
Егер жарықты екі поляризатордан қатар өткізсе, онда өткен жарықтың интенсивтілігі Малюс заңынан анықталады
,
(7.13)
мұндағы
-
екі поляризатор арасындағы бұрыш.
Екі
орта шекарасына түскен жарық, шағылу
немесе сыну кезінде өзінің поляризациясын
өзгертеді. Түсу бұрышы нөлден өзгеше
болса, шағылған және сынған сәулелер
жартылай поляризацияланады. Шағылған
жарықтың электр өрісінің кернеулік
векторы түсу жазықтығына перпендикуляр
жазықтықта, ал сынған жарықтікі –
параллелль жазықтықта тербеледі. Белгілі
бір
бұрышта
ғана (Брюстер бұрышы)
(7.14)
шағылған жарық толығымен поляризацияланады.
8 Дәріс. Электрмагниттік сәуле шығарудың кванттық табиғаты
Дәрістің мақсаты:
- электрмагниттік сәуле шығарудың сипаттамаларымен танысу;
- жылулық сәуле шығару заңдарын меңгеру.
Физика классикалық және кванттық физика болып бөлінеді. 1900 жылы М.Планк кванттар гипотезасын тұжырымдады. 1926 жылы микроәлем физикасының теориясы жасалды.
8.1 Жылулық сәуле шығарудың сипаттамалары мен қасиеттері
Жылулық сәуле шығару дегеніміз заттың ішкі энергиясы (атомдар мен молекулалардың жылулық қозғалысының энергиясы) өзгергенде шығарылатын электромагниттік сәуле шығару.
Температурасы абсолюттік нольден жоғары кез келген агрегаттық күйдегі барлық денелер жылулық сәуле шығарады. Жылулық сәуле шығару интенсивтілігі мен оның спетрлік құрамы сәуле шығаратын дененің оптикалық қасиеттері мен температурасына тәуелді.
Қалыпты температурада барлық денелер көрінбейтін инфрақызыл толқындар шығарады, ал жоғары температурада (1000 К шамасында) жарқырай бастайды (қызыл жарқырау). 2000 К-нен жоғары температурада сары және ақшыл жарық шығарады. Жылулық сәуле шығару үшін жарық сәулелерінің таралу, шағылу, сыну заңдары орындалады.
Жылулық сәуле шығару – затпен термодинамикалық тепе-теңдікте бола алатын жалғыз сәуле шығару.
Егер қыздырылған денені қабырғасы жылу өткізбейтін қуысқа орналастырсақ, онда біраз уақыт өткеннен кейін статистикалық тепе-теңдік орнайды: дене бірлік уақытта қанша энергия шығарса, сонша энергия қабылдайды.