Файл: Пояснительная записка Соискатель, студент группы элб16 Догадин Р. А.docx

Рисунок 1.6 – Структура стенда с использованием ПЛК

Самым простым является управление через интерфейс USB. На рисунке 1.7 приведено подключение USB-кабеля. На компьютер устанавливается

программное обеспечение для преобразователя частоты конкретного производителя. В нашем случае используется программное обеспечение FRConfigurator фирмы MELSOFT. На рисунке 1.8 приведен пользовательский интерфейс программы.

FR-Configurator позволяет производить мониторинг, диагностику, настройку и управление преобразователем частоты. Перед началом работы с преобразователем частоты производится предварительная настройка программы, после её выполнения все параметры сохраняются в отдельный файл и при дальнейших запусках её выполнение не требуется.



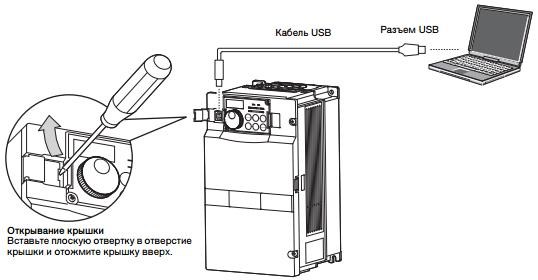
Рисунок 1.7 – Подключение преобразователя частоты через USB



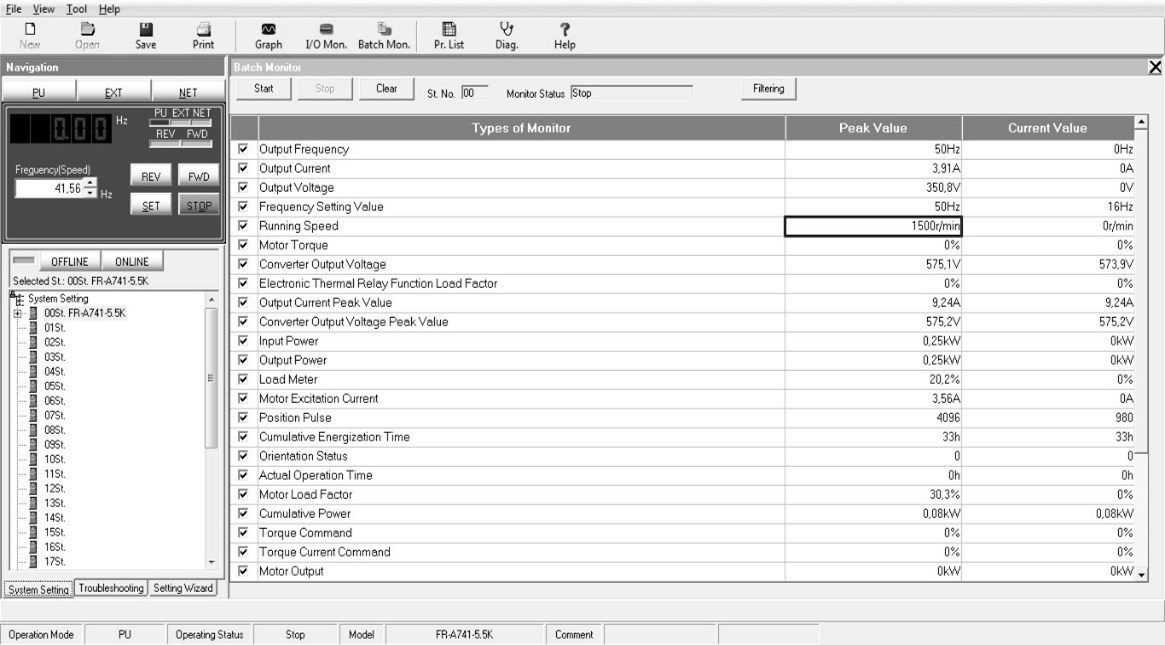
Рисунок 1.8 – Рабочее окно программы FR-Configurator

Вывод: управление преобразователем частоты при помощи персонального компьютера позволяет осуществлять регулирование скорости за счет изменения входного напряжения и его частоты, а также отслеживать выходные параметры такие, как ток, напряжение и его частота, потребляемая мощность, скорость вращения ротора и т.д. Также при помощи программы FR-Configurator можно

получить зависимости выходных параметров от времени работы электродвигателя в виде графиков, что делает работу стенда более наглядной.

1.1.4 Управление с сенсорной панели оператора

Панель оператора – устройство, предназначенное для внешнего управления технологическим процессом. К преобразователю частоты она может быть подсоединена непосредственно через интерфейс RS-422, либо через ПЛК. На лабораторном стенде панель оператора подключена через ПЛК по схеме, которая приведена на рисунке 1.9.



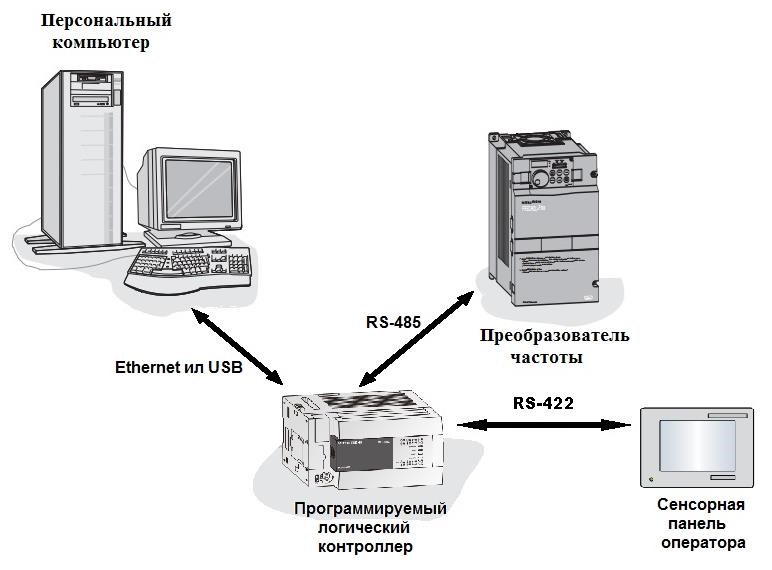
Рисунок 1.9 – Структура стенда при использовании сенсорной панели оператора

Панель оператора используется для визуализации и упрощения управления электроприводом. Существуют монохромные панели оператора и цветные. На стенде установлена цветная сенсорная панель Mitsubishi GT1055-QSBD. Использование цветной сенсорной панели даёт возможность создавать интуитивно понятные интерфейсы, где отображается не только числовая информация о параметрах объекта управления, но и графическая, где представлен сам технологический процесс. Её настройка и графическое оформление создается в программе

---

GT Designer.

Вывод: лабораторный стенд «Интеграл» состоит из преобразователя частоты Mitsubishi FR-A741, асинхронного двигателя ELDIN A100L4FБУЗ и персонального компьютера. Управление электроприводом может осуществляться посредством панели управления на преобразователе частоты, персонального компьютера через программу FR-Configurator, аналоговой панели, сенсорной панели. Данный лабораторный стенд позволяет изучить принцип работы частотно-регулируемого электропривода, изучить принцип скалярного и векторного регулирования скорости вращения электродвигателя. Также при управлении стендом с помощью персонального компьютера имеется возможность снимать выходные параметры стенда в виде графиков, что упрощает анализ работы стенда.

После того, как мы рассмотрели устройство и принцип работы лабораторного стенда «Интеграл», перейдем к математическому описанию его элементов.

---

2 Математическое описание объектов лабораторного стенда «Интеграл»

Перед моделированием режимов работы асинхронного частотно-

регулируемого электропривода, в частности асинхронного двигателя, в пакете программ MatLab, целесообразно рассмотреть их математические модели.

2.1 Математическое описание асинхронного двигателя

Для математического описания процессов в асинхронном двигателе часто используются дифференциальные уравнения обобщенной двухфазной машины переменного тока, полученные при общепринятых допущениях (без учета потерь в стали, высших гармоник магнитного поля с равномерным воздушным зазором и напряжение питания, которые представляют собой симметричную систему синусоидальных напряжений). Также в описании предполагается, что параметры схемы ротора приведены к схеме статора.

Исходные уравнения, записанные с использованием обобщенных пространственных векторов в системе координат, вращающихся с произвольной скоростью ω_к (при отсутствии внешних источников напряжения в роторных цепях) имеют вид:

????

????̅̅₁̅ = ????̅₁ ∙ ????₁ + ̅????̅̅₁̅ + ???? ∙ ????_к ∙ ̅????̅̅₁̅;

????????

(2.1)

????

0 = ????̅₂ ∙ ????₂ + ̅????̅̅₂̅ + ???? ∙ (????_к − ????_э) ∙ ̅????̅̅₂̅;

????????

???? ,(2.2)

где ????̅̅₁̅ – обобщенный вектор напряжения статора; ????̅₁, ????̅₂ – обобщенные векторы тока соответственно статора, ротора; R₁, R₂ – активное сопротивление обмотки статора, ротора; ̅????̅̅₁̅, ̅????̅̅₂̅ – обобщенные векторы потокосцепления соответственно статора, ротора; ω_к – электрическая угловая скорость вращения координатных осей; ω_э – электрическая угловая скорость вращения ротора,

????_э = ???? ∙ ????_п, (2.3)

где ω – механическая угловая скорость ротора; M – электромагнитный момент, развиваемый двигателем; p_п – число пар полюсов асинхронной машины; L₀ – индуктивность намагничивающего контура;

---

J_m – знак, указывающий на то, что берется только вещественная часть комплекса.

Для исследования переходных процессов система уравнений (2.1) и уравнение (2.2) дополняются уравнением движения электропривода:

???? ????????_э (2.4)

???? − ????_с = ∙ ,

????_п ????????

где M_с – момент статической нагрузки; J – приведенный к валу суммарный момент инерции электропривода, J = J_дв + J_мех; J_дв и J_мех – момент инерции двигателя и приведенный к валу двигателя момент инерции механизма.

Система уравнений (2.1), записанная через проекции обобщенных векторов на ортогональные оси u, jv координатной плоскости, вращающейся с произвольной скоростью ω_к, имеет следующий вид:

????1???? = ????1 ∙ ????1???? + ???? ∙ ????1???? − ????к ∙ ????1????????;

????1???? = ????1 ∙ ????1???? + ???? ∙ ????1???? − ????к ∙ ????1????;

(2.5)

0 = ????₂ ∙ ????_2???? + ???? ∙ ????_2???? − (????_к − ????_э) ∙ ????_2????;

0 = ????₂ ∙ ????_2???? + ???? ∙ ????_2???? − (????_к − ????_э) ∙ ????_2????,

где p – оператор дифференцирования.

В этом случае электромагнитный момент, развиваемый асинхронным двигателем, может быть определен из выражения

???? . (2.6)

Рациональное значение ω_к зависит от типа решаемой задачи и, как правило, принимает одно из следующих значений: ω_к = 0 (в этом случае принято обозначать координатные оси α, jβ); ω_к = ω_0э (координатные оси x, jy); ω_к = ω_э (координатные оси d, jq). Здесь ω_0э – электрическая угловая скорость электромагнитного поля статора. Эта величина соответствует электрической скорости холостого хода. Заметим, что механическая угловая скорость холостого хода, она же – синхронная скорость, ω₀ = ω_0э/p_п.

Следует заметить, что, обозначая угловую скорость через ω и измеряя ее с^-1, зачастую определение «угловая» опускают и оперируют термином «скорость».

Связь между полным потокосцеплением статора ̅????̅̅₁̅, ротора ̅????̅̅₂̅, главным потокосцеплением ̅????̅̅₀̅ и токами статора i₁ и ротора i₂ ненасыщенной асинхронной машины выражается следующим образом:

̅????̅

---

;

(2.7)

̅????̅ ,

где L_s = L₀ + L_1σ – полная индуктивность обмотки статора; L_1σ – индуктивность рассеяния обмотки статора; L_r = L₀ + L_2σ – полная индуктивность обмотки ротора; L_2σ – индуктивность рассеяния обмотки ротора.



Если учесть, что ????₀ = ????₁ + ????₂, то выражения (2.7) можно записать в следующем виде:

̅????̅ ;

(2.8)

̅????̅ ,

где ̅????̅̅₀̅ = ????₀ ∙ ????₀; ????_1???? ∙ ????₁ = ψ_1????; ???? _???? – потокосцепление рассеяния соответственно статора, ротора.

Запишем выражения для потокосцеплений через проекции на оси комплексной плоскости:

ψ1???? = ψ0???? + ????1???? ∙ ????1????;

(2.9)

ψ1???? = ψ0???? + ????1???? ∙ ????1????;

ψ2???? = ψ0???? + ????2???? ∙ ????1????; ψ2???? = ψ0???? + ????2???? ∙ ????1????; ψ0???? = ????0 ∙ ????0????; ψ0???? = ????0 ∙ ????0????.

При необходимости учета насыщения целесообразно использовать следующую систему уравнений:



ψ1 = ψ0 + ψ1????;



ψ2 = ψ0 + ψ2????;

;

(2.10)



????₀ = ????₁ + ????₂;

; .



В системе уравнений (2.10) переменная индуктивность ????₀(|????₀|), с помощью

которой учитывается насыщение двигателя по главному магнитному пути, рассчитывается по кривой намагничивания:

ψ₀(|????₀|)

????₀(|????₀|) =,

(|????₀|)

---