Файл: Пояснительная записка Соискатель, студент группы элб16 Догадин Р. А.docx

где ψ₀(|????₀|) – нелинейная функция (характеристика намагничивания,



определяющая связь между модулем |ψ₀| результирующего вектора главных



потокосцеплений ψ₀ и модулем |????₀| результирующего вектора



намагничивающих токов ????₀.

В некоторых случаев для вычисления индуктивности целесообразно использовать выражение

????₀(|ψ₀|) = ,

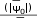????₀(|ψ₀|)



где ????₀(|ψ₀|) – обратная по отношению ψ₀(|????₀|) нелинейная функция.

Представленные выше уравнения могут быть использованы для анализа как переходных, так и установившихся режимов.

При анализе установившихся режимов на переменной частоте питающего напряжения (f₁ ≠ const) примем в системе уравнений (2.1) скорость ????_к = ????_0э = 2 ∙ ???? ∙ ????₁, а производные равными нулю, тогда получим следующую модель, описывающую установившийся режим работы двигателя:

???? ;

;



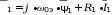ψ1 = ψ0 + ψ1????;



ψ2 = ψ0 + ψ2????;

;

(2.11)



????₀ = ????₁ + ????₂;

;

;

???? × ????₁];

???? = ????_с.

Исходя из уравнений установившегося режима строим схему замещения асинхронного электродвигателя при переменном значении частоты источника питания f₁. Для этого в уравнениях электрического равновесия напряжений пренебрежем результирующими векторами полных потокосцеплений обмоток

---

статора ψ₁ и ротора ψ₂. В полученных уравнениях выразим результирующие



векторы главных потокосцеплений ψ₀ и потокосцеплений рассеяния обмоток



статора ^ψ_1???? и ротора ^ψ_2???? через результирующие токи соответственно ????₀, ????₁ и ????₂.

После этого получим уравнения следующего вида:

???? ;

(2.12)

????₂

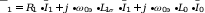0 = ∙ ????₂ + ???? ∙ ????_0э ∙ ????_2???? ∙ ????₂ + ???? ∙ ????,

????

где ???? = ???? ????0−0???? = ????0????э−0э????э – скольжение; ????0 2∙????????п∙???? ; ????0э = 2 ∙ ???? ∙ ????1.

Системе уравнений (2.12) соответствует схема замещения асинхронного двигателя при переменной частоте питающего напряжения, приведенная на русинке 2.1.



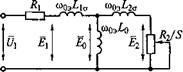
Рисунок 2.1 – Схема замещения асинхронного двигателя при переменной частоте питающего напряжения

Учтем насыщение асинхронного двигателя в схеме с помощью переменного



коэффициента L₀, являющегося функцией тока намагничивания |????₀|.

Наведенные в электромагнитных контурах ЭДС можно записать следующим образом:

???? ;

???? ;

???? ;

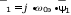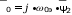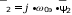Представленная на рисунке 2.1 схема замещения может быть использована при анализе установившихся режимов асинхронного двигателя при частотном способе регулирования угловой скорости.

В системах асинхронных электроприводов с регулированием напряжения основной гармоники переменного напряжения или добавочного сопротивления в роторе частота питающего напряжения остается неизменной и равной номинальному значению. Для следующих случаев уравнения статических режимов приобретают следующий вид:

---

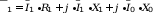???? ; (2.13)

????,

при ????1 = ????0э.ном ∙ ????1????; ????′2 = ????0э.ном ∙ ????2????; ????0 = ????0э.ном ∙ ????0; ????1, ????′2 – индуктивные сопротивления рассеяния обмоток соответственно статора и ротора; ????₀ – индуктивное сопротивление контура намагничивания.



В уравнениях статических режимов (2.13) с помощью ????′₂, ????′₂, ????′₂ обозначены параметры ротора, приведенные к параметрам обмотки статора, а



выражение ????₀ ∙ ????₀ представляет собой ЭДС контура намагничивания:

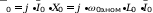???? .(2.14)

С учетом (2.14) система уравнений (1.15) будет представлять собой систему уравнений статического режима работы асинхронного двигателя при f₁ = f_1ном, которому соответствует Т-образная схема замещения, представленная на рисунке 2.1.

Обычно для облегчения процедуры анализа статических режимов используют Г-образную схему замещения, для этого подключают контур намагничивания к зажимам питающего напряжения. Это не вносит существенных погрешностей в расчеты. Г-образная схема замещения асинхронного электродвигателя в статических режимах приведена на рисунке

2.2. В такой схеме ток ????₀ = ????₁/????₀ остается в процессе работы двигателя постоянным и не зависит от скорости (скольжения) двигателя.



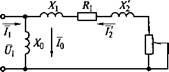
Рисунок 2.2 – Г-образная схема замещения асинхронного двигателя в статических режимах

Приведенные при f₁ = f_1ном уравнения статических режимов (2.13) и схема замещения, представленная на рисунке 2.2, могут быть использованы для исследования свойств и характеристик асинхронного электропривода, как при регулировании напряжения U₁, подводимого к статору, так и при регулировании добавочных сопротивлений ротора R_2доб. Это реализуется в асинхронных двигателях с контактными кольцами, для чего в схеме замещения вместо ????′

---

₂ используется значение ????′_2∑ = ????′₂ + ????′_2доб. Для двигателей с короткозамкнутым ротором ????′_2∑ = ????′₂. Тогда ток ротора

????₁

???? .

(2.15)

При известном токе ротора можно определить статорный ток:

???? , (2.16)

где ????_1ном и ????′_2ном – соответственно номинальный ток статора, приведенный номинальный ток ротора.

Выражение (2.16) может быть преобразовано следующим образом:

2 = ????02 + (????12ном − ????02) ∙ ???? ∙ ???? ,(2.17)

????1

????ном ∙ ????ном

где ????_ном и ????_ном – соответственно номинальный момент и скольжение двигателя.

Момент двигателя

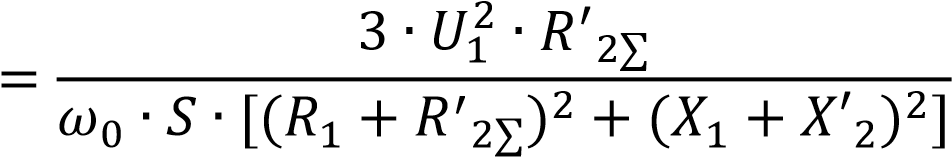???? .(2.18)

Называемый критическим максимальный момент двигателя

????_к 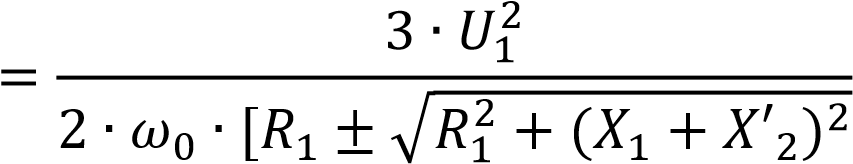.(2.19)

Критическое скольжение, соответствующее критическому моменту,

????′2∑

????_к .(2.20)

В формулах 2.19 и 2.20 знак «+» соответствует двигательному режиму работы двигателя, а знак «–» тормозному. Используя данные формулы можно получить уточненную формулу Клосса для записи зависимости момента асинхронного двигателя от скольжения:

2 ∙ ????к ∙ (1 + ???? ∙ ????к) ???? = , ???? ????к + 2 ∙ ???? ∙ ????к + ????к ???? ???? где ???? = 1⁄????′2∑.

(2.21)

В ряде случаев используют упрощенную формулу Клосса, приняв a = 0. Тогда

2 ∙ ????_к

???? = ,(2.22)

???? + ????_к

????_к ????

Математическое описание переходных и установившихся процессов в асинхронном двигателе показывает, что управляющими воздействиями, изменяющими характеристики двигателя, являются амплитуда (или среднеквадратичное значение) переменного напряжения питания, частота и амплитуда переменного напряжения

---

, подаваемого на статор, общее активное сопротивление цепей ротора (для двигателей с фазным ротором, когда возможно изменение величины дополнительного сопротивления Ротора).

Вывод: управляющими воздействиями, изменяющими параметры асинхронного двигателя, являются амплитуда (или действующее значение) переменного питающего напряжения, частота и амплитуда переменного напряжения, подводимого к статору.

В современных системах электропривода регулирование указанных параметров производится с использованием различных типов полупроводниковых преобразователей, поэтому исходные выражения должны быть дополнены математическим описанием и моделями рассматриваемых типов преобразователей с учетом систем управления ими, что позволит анализировать процессы в системе «преобразователь – асинхронный двигатель».

2.2 Математическое описание элементов силовой части

---