Файл: Пояснительная записка Соискатель, студент группы элб16 Догадин Р. А.docx

преобразователь частоты – асинхронный двигатель (ПЧ – АД)

Рассмотрим математическую модель типичной системы ПЧ – АД, схема силовых цепей которой представлена на рисунке 2.3. В состав системы ПЧ –АД входят трехфазный мостовой автономный инвертор напряжения (АИН) с широтно-импульсной модуляцией (ШИМ) выходного напряжения и АД с короткозамкнутым ротором. Источником напряжения для АИН служит неуправляемый выпрямитель с коммутирующим реактором на входе и LC-фильтром на выходе. Обмотка статора двигателя соединена в звезду и подключена через реактор к выходу инвертора по схеме без нулевого провода.



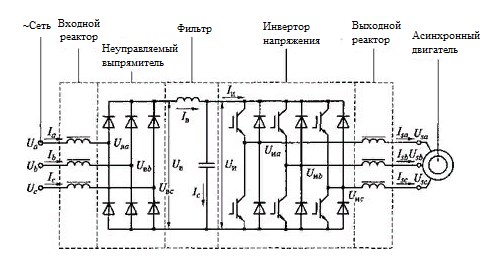
Рисунок 2.3 – Схема силовых цепей системы ПЧ – АД

При составлении математической модели силовой части ПЧ – АД прибегнем к методу структурного моделирования, описывая отдельно каждый элемент системы – АД, АИН с выходным реактором и неуправляемых выпрямитель с входным коммутирующим реактором и LC-фильтром на выходе.

В качестве исходной модели асинхронного двигателя с короткозамкнутым ротором примем следующую систему скалярных уравнений:

????1???? = ???? ∙ ????1???? − ????к ∙ ????1???? + ????1 ∙ ????1????;

????1???? = ???? ∙ ????1???? − ????к ∙ ????1???? + ????1 ∙ ????1????;

0 = ???? ∙ ????_2???? − (????_к − ????_э) ∙ ????_1???? + ????₂ ∙ ????_2????;

0 = ???? ∙ ????_2???? − (????_к − ????_э) ∙ ????_1???? + ????₂ ∙ ????_2????;

????1???? = ????0???? + ????1???? ∙ ????1????;

????1???? = ????0???? + ????1???? ∙ ????1????; (2.23)

????2???? = ????0???? + ????2???? ∙ ????2????;

????2???? = ????0???? + ????2???? ∙ ????2????;

????0???? = ????0 ∙ ????0????;

????0???? = ????0 ∙ ????0????;

????₀???? = ????₁???? + ????₂????;

????₀???? = ????₁???? + ????₂????;

???? ;

???? ∙ ????_э = ????_п ∙ ????⁻¹ ∙ (???? − ????_с),

где ????_1????, ????_1????, ????_1????, ????_1????, ????_1????, ????_1???? – соответственно преобразованные напряжения,

токи и полные потокосцепления обмотки статора;

????_2????, ????_2????, ????_2????, ????_2???? – преобразованные токи и полные потокосцепления обмотки ротора; ????_0????, ????_0????, ????_0????, ????_0???? – результирующие токи намагничивания и главные потокосцепления.

---

Заметим, что насыщение магнитной цепи машины в модели АД учитывается с помощью переменного коэффициента L₀, зависящего от тока намагничивания и определяемого зависимостью ????₀ = ????₀(????₀), где ????₀ – модуль результирующего вектора намагничивающих токов, ????₀ = (????₀²_???? + ????₀²_????)^1/2. Для линейной магнитной цепи коэффициент L₀ является постоянной величиной.

Автономный инвертор напряжения с ШИМ представляет собой сложное нелинейное дискретное устройство. Несущая частота АИН на полупроводниковых приборах составляет 2…16 кГц. При таком высоком уровне несущей частоты для построения математических моделей АИН используется метод выделения полезных сигналов путем усреднения мгновенных значений переменных в пределах периода несущей частоты. В этом случае инвертор напряжения с симметричной двухсторонней ШИМ во вращающейся прямоугольной системе координат описывается следующей системой уравнений:

????_???? ;

1 (2.24)

????_???? ;

????и???? = ????и ∙ ????????;

????и???? = ????и ∙ ????????;

????_и ,

где ???? – преобразованные задающие воздействия; ????_????, ????_???? – усредненные коммутационные функции; ????₀ – амплитуда опорного сигнала; ????_и – напряжение источника питания инвертора; ????_и????, ????_и???? – усредненные выходные напряжения

инвертора; ????_1????, ????_1???? – усредненные выходные токи инвертора.

Выходные реакторы моделируются уравнением:

???? ∙ ????₁???? = ????⁻_р.¹_вых ∙ (????_и???? + ????_к ∙ ????_р.вых ∙ ????₁???? − ????_р.вых ∙ ????₁???? − ????₁????);

(2.25)

???? ∙ ????₁???? = ????⁻_р.¹_вых ∙ (????_и???? + ????_к ∙ ????_р.вых ∙ ????₁???? − ????_р.вых ∙ ????₁???? − ????₁????), где ????_р.вых, ????_р.вых – активное сопротивление и индуктивность выходного реактора.

---

Для того, чтобы учесть главные особенности неуправляемого выпрямителя при анализе энергетических характеристик системы полупроводниковый преобразователь частоты – асинхронный двигатель в переходных и установившихся режимах используем математическую модель, учитывающую только первую гармонику коммутационной функции выпрямителя. В прямоугольной системе координат, вращающейся с произвольной угловой скоростью ????_к, модель неуправляемого выпрямителя с входным реактором может быть описана следующей системой уравнений:

????_???? = ????_в???? + ????_р.вых ∙ ???? ∙ ????_???? − ????_к ∙ ????_р.вых ∙ ????_???? + ????_р.вых ∙ ????_????;

????_???? = ????_в???? + ????_р.вых ∙ ???? ∙ ????_???? − ????_к ∙ ????_р.вых ∙ ????_???? + ????_р.вых ∙ ????_????;

(2.26)

????_в???? = ∙ cos(????_???? − ????_к) ;

????

????в????;

????

????в ????в???? ∙ ????в????);

???????? = ????в ∙ ????в????;

???????? = ????в ∙ ????в????; ????_к = ???? ∙ ????_к,

где ????_????, ????_????, ????_????, ????_???? – преобразованные основные гармоники напряжений и токов сети; ????_в????, ????_в???? – преобразованные основные гармоники напряжений на силовом входе неуправляемого выпрямителя; ????_в????, ????_в???? – преобразованные основные гармоники коммутационных функций неуправляемого выпрямителя; ????_???? – угол поворота обобщенного вектора коммутационной функции выпрямителя, или результирующего вектора тока сети, относительно фазы A напряжения сети; ????_к – угол поворота системы координат; ????_в, ????_в – напряжение и ток на выходе выпрямителя; ????_р.вых, ????_р.вых – активное сопротивление и индуктивность выходного реактора.

Модель LC-фильтра на выходе неуправляемого выпрямителя описывается линейными уравнениями:

???? ;

???? ????_с; (2.27)

????_с = ????_в − ????_и,

---

где ????_р.ф, ????_р.ф – активное сопротивление и индуктивность сглаживающего реактора LC-фильтра; ????_б.ф – емкость конденсаторной батареи фильтра; ????_с – ток конденсатора фильтра.

Вывод: воздействиями, изменяющими характеристики асинхронного двигателя, являются амплитуда (или среднеквадратичное значение) переменного напряжения питания, частота и амплитуда переменного напряжения, подводимого к статору. Преобразователь частоты состоит из входного реактора, неуправляемого выпрямителя, сглаживающего фильтра, автономного инвертора с широтно-импульсной модуляцией напряжения и выходного реактора. После рассмотрения математических описаний элементов лабораторного стенда, перейдем к моделированию в пакете программ MatLab.

---

3 Моделирование режимов работы частотно-регулируемого

электропривода в пакете программ MatLab

Пакет программного обеспечения MatLab включает в себя ядро компьютерной алгебры Maple и пакет расширений Simulink, а также множество других пакетов расширений, которые позволяют моделировать сложные электротехнические устройства.

Библиотека блоков SimPowerSystems является частью многих

дополнительных библиотек Simulink, ориентированных на моделирование электромеханических и электроэнергетических систем и устройств. Библиотека включает в себя модели пассивных и активных электротехнических элементов, источников энергии, электродвигателей, трансформаторов, линий электропередач и другого оборудования. Также есть раздел блоков, которые используются для моделирования устройств силовой электроники, включая системы управления ими.

Специальные функции Simulink и SimPowerSystems позволяют не только моделировать работу устройств во временной области, но и выполнять различные виды анализа таких устройств. В частности, можно рассчитать установившийся режим работы системы при переменном токе, получить частотные характеристики и выполнить гармонический анализ токов и напряжений.

Целью моделирования является построение характеристик зависимости электромагнитного момента и угловой скорости вращения электродвигателя от времени запуска, а также для определения перерегулирования, смещения и времени перехода. Для начала смоделируем простую модель прямого пуска асинхронного двигателя для проверки параметров, а затем модель с преобразователем частоты и автономным инвертором напряжения.

3.1 Моделирование прямого пуска асинхронного двигателя ELDIN

A100L4FБУЗ

Модель представляет собой принципиальную схему, состоящую из источников синусоидального напряжения, асинхронного двигателя с короткозамкнутым ротором, блока для измерения основных параметров двигателя, осциллографа для измерения токов статора и ротора, электромагнитного момента и скорости вращения ротора, также в состав модели входит измеритель активной и реактивной мощности. Модель представлена на рисунке 3.1.

---