ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Дробно рациональные уравнения с параметром
Алгоритм решения:
а) найти область допустимых значений уравнения;
б) решить целое рациональное уравнение;
в) найти те значения параметра, при которых найденные корни целого рационального уравнения являются посторонними, т.е. исключить из корней целого уравнения, т.е., которые обращаю в нуль общий знаменатель;
г) сформулировать ответ.
1) Решить уравнение
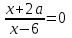.▼ ОДЗ: x – 6 0
Данное уравнение равносильно системе
; 
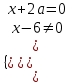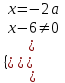
Найдем недопустимые значения параметра а. Подставим корень х = -2а в ограничение: -2а - 6 = 0, а = - 3. При а = - 3 корней нет.
Отв. х = -2а при а(-;-3)(-3; ); при а = - 3 корней нет.
2) Решить уравнение
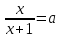.▼ ОДЗ: x + 1 0
Преобразованное уравнение на ОДЗ: (1 - а)х = а
При 1 – а = 0, а = 1 уравнение не имеет корней.
При а 1 получаем х =
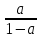.Найдем недопустимые значения параметра а. Подставим корень х =
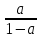в ограничение: 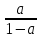+ 1 = 0, 1 = 0 (ложь), корней нет.Отв. при а 1, х =
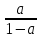; при а = 1 корней нет.3) Решить уравнение
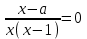.▼ ОДЗ: х 0, x - 1 0.
Преобразованное уравнение на ОДЗ: х = а
Найдем недопустимые значения параметра а. Подставим корень х = а последовательно в оба ограничения:
а = 0, х = 0 – посторонний корень
а - 1= 0, а = 1, х = 1 – посторонний корень
Отв. при а = 0; 1 корней нет; при а 0; 1 х = а.
4) Решить уравнение
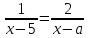.▼ ОДЗ: х - 5 0, x - а 0.
Преобразованное уравнение на ОДЗ: х = 10 - а
Найдем недопустимые (запрещенные) значения параметра
а. Подставим корень х = 10 - а последовательно в оба ограничения:
10 - а – 5 = 0, а = 5
10 - а – а = 0, а = 5
Значение а = 5 запрещено, а х = 5 – посторонний корень.
Отв. при а = 5 корней нет; при а 5 х = 10 - а.
Замечание. Решение дробно-рациональных уравнений с параметрами нередко сводится к решению квадратных уравнений, но с учетом ограничений на допустимое значение неизвестного. Рассмотрим общие приемы, используемые при решении дробно-рациональных уравнений с параметрами:
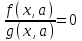.Постановка задачи
Дано: квадратное уравнение f(x,a) = 0 относительно х и ограничение
g(x,a) = 0
Требуется: найти решение уравнения с учетом ограничения.
Первый способ. Решаем уравнение f(x,a) = 0, находим корни х1 = р1(а),
х2 = р2(а). Подставляем найденные корни в ограничение. Решаем уравнения g(рi(а)) = 0 и находим множества Аi «запрещенных» значений параметра а. Вычисляем значения остальных (вторых) корней на запрещенных значениях для одного из корней. И так перебираем все корни.
Второй способ. Решаем ограничение g(x,a) = 0, находим его корни x = rk(a).
Подставляем найденные корни в уравнение. Решаем уравнение f(rk(a)) = 0 и находим akm. Для уравнения f(x,akm) = 0 корень x = rk(akm) является запрещенным, т.к. он обращает в ноль функцию g(x,a). Нужно найти остальные (вторые) корни уравнения f(x,akm) = 0, используя теорему Виета, и выяснить, не являются ли они запрещенными.
1)