Уравнения с одной переменнойУравнением с одной переменнойх называется выражение f(x) = g(x), содержащее переменную величину х и знак равенства.Решением (корнем) уравнения называется всякое значение неизвестного х, при подстановке которого в обе части уравнения получаем верное числовое равенство.Решить уравнение - значит найти все его корни (решения) или доказать, что корней (решений) нет.Областью допустимых значений (ОДЗ) уравнения называется множество всех значений неизвестного, для которых математические выражения, входящие в лбе части уравнения, имеют смысл.Два уравнения называются равносильными (эквивалентными), если они имеют одно и то же множество решений.Обозначение: f(x) = g(x)  h(x) = (x).Таким образом, два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.В процессе решения уравнения его стараются заменить более простым, но равносильным данному.При некоторых преобразованиях исходного уравнения могут появиться посторонние корни или их потеря. Если в результате преобразований заменить исходное уравнение следствием, то при решении нового уравнения потери корней не происходит, но можно получить посторонние корни, от которых избавляются проверкой.Таким образом, при решении должны следить, чтобы в результате преобразований исходного уравнения не происходило потеря корней, т.е. чтобы новое уравнение было следствием другого или равносильно ему.Линейные уравнения.Линейным уравнением с одной переменной называется уравнение вида ах = b, где a – коэффициент при переменной, b – свободный член.Замечание. Будем считать a > 0 – стандартный вид.Рассмотрим различные случаи решения уравнения:а) a ≠ 0 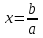 - единственное решение;б) 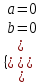; 0∙х = 0 (истина) х = (-∞; ∞) – бесконечное множество решений;в) 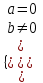; 0 = b (ложь)  нет решенийУпр. Решить уравнения.

---

1) 6(x+ 1) = 3 – 2x, 6x + 6 = 3 – 2x, 8x = -3, x = -3/8.2) 2x+ 5 = 2(x– 7), 2x + 5 = 2x- 14, 0 = -19 (ложь)  нет решений.3) 3(x+ 3) + х = 9 + 4х, 3x + 9 + х = 9 + 4x, 0 = 0 (истина)  х = (-∞; ∞).4) 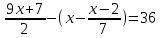, 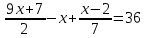. (Общ. знамен. = 14)63x + 49 – 14x + 2x – 4 = 504, 51x = 459, x = 9.5) 4x + 11 – 8( 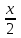- 1) = 19, 4x + 11 – 4x + 8 = 19, 0 = 0 (истина)  х = (-∞; ∞).6) 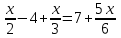, (Общ. знамен. = 6), 3x – 24 + 2x = 42 + 5x0 = 66 (ложь)  нет решений.7) (3x + 9)(2х - 4) = 0 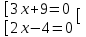; 3x = -9, x = -32x = 4, x = 2Отв. х = -3; 2Квадратные уравненияУравнение вида ax² + bx + c = 0, где a, b, c– действительные числа, а ≠ 0, называется квадратным.Если а ≠ 1, то квадратное уравнение называется приведенным, и записывается обычно в виде x² + px + q = 0.Если в квадратном уравнении хотя бы один и коэффициентов b или c равен нулю, то такое уравнение называется неполным квадратным уравнением.Неполные квадратные уравненияI Пусть b = 0, тогда ax² + c = 0, ax² = -c, х² = -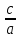Если х² = - 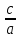> 0, то имеем два корня; если х² = - 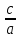< 0  корней нет.1)4x² - 9 = 0, х² = 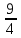> 0  х = ±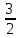 2)3x² + 15 = 0, х² = - 5 < 0  корней нет.II Пусть с = 0, тогда ax² + bx = 0, х(ax + b) = 0  х₁ = 0, х₂ = - 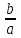1)3x² + 9х = 0, 3х(x + 3) = 0  х₁ = 0, х₂ = -3III Пусть b = с = 0, тогда ax² = 0  х = 0 – корень кратности 2Решение уравнения ax² + bx + c = 0Выражение D = b²

---

– 4ac называется дискриминантом квадратного уравнения.

D > 0 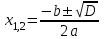 - два различных корня

D = 0 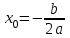 - один корень кратности 2

D < 0  действительных корней нет.

Теорема Виета. Если приведенное квадратное уравнение

x² + px + q = 0 имеет корни, то



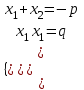
Упр. Не решая уравнение 2x² + 2x - 3 = 0, найти

а) х₁ + х₂; б) х₁х₂; в) 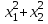; г)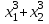

▼ Приведенное квадратное уравнение x² + x – 1,5 = 0

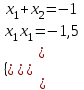- теорема Виета

а) х₁ + х₂ = -1; б) х₁х₂ = -1,5;

в) ;

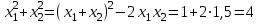г) ▲

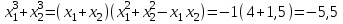Разложение квадратного трехчлена на множители

Квадратным трехчленом называется выражение ax² + bx + c.

Если D > 0, то ax² + bx + c = а(х - х₁)(х - х₂), где х₁, х₂ – корни квадратного уравнения ax² + bx + c = 0.

Если D = 0, то ax² + bx + c = а(х - х₀)², где х₀ –корень соответствующего квадратного уравнения.

Если D < 0, то квадратный трехчлен не разлагается на множители.

Упр. Разложить квадратный трехчлен на множители

1) 2x² – 5x + 2 = 2(x - 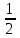)(x - 2)

D = 9 > 0, .

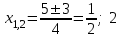2) 4x² – 4x + 1 = 4(x + 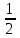)²

D = 0, x₀ =- = - .

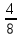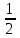3) 3x² + 3x + 8 – не разлагается, т.к. D = 9 – 36 < 0.

Упр. Решить уравнение

1) (2x + 7)² = (2x - 7)², 4x² + 28x + 49 = 4

---

x² – 4x + 1, 32x = -48, x = 1,52) (x - 6)² = 24x, x² - 12x + 36 = – 24x, x² - 12x 32x + 36 = 0, D = 0, x =- 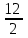= - 6.3) (x - 1)³ = -8, x – 1 = -2, x = - 1.4) x² + 5x - 6 = 0, D = 49 > 0, 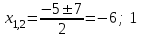.5) 2x² – 3x + 1 = 0, D = 1 > 0, 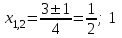.6) 2x² – 3x + 4 = 0, D =-23 < 0, корней нет.7) 9x² + 6x + 1 = 0, D = 0, 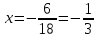- один корень кратности 2.Рациональные уравненияУравнение f(x) = g(x) называется рациональным, если f(x), g(x) – рациональные выражения.Рациональное уравнение называется целым, если в нем нет деления на выражение, содержащее х. К целым уравнениям относятся, например, линейные и квадратные уравнения.Если в рациональном уравнении есть деление на выражение содержащее х, то уравнение называется дробно-рациональным. Например, 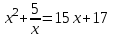.Решение дробно рационального уравнения сводится к замене исходного уравнения целым уравнением.Чтобы решить дробно рациональное уравнение, нужно:1) найти общий знаменатель уравнения;2) заменить данное уравнение целым, умножив обе его части на общий знаменатель;3) решить получившееся целое уравнение;4) исключить из его корней те, которые обращают в нуль общий знаменатель.Упр. 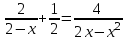Решить уравнение1) ▼ Общий знаменатель 2х(2 – х) ≠ 0, х ≠ 0; 2.Умножим обе части уравнение на общий знаменатель (подписывая дополнительные множители для каждой дроби, освободимся от знаменателя)2∙2х + 1∙х(2 – х) = 4∙2, x² - 6x + 8 = 0, х = 2; 4Корень х = 2 исключаем. Отв. 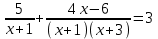5▲2) ▼ Общий знаменатель (х + 1)(х + 3) ≠ 0, х ≠ -1; 3.5∙(х + 3) + (4х - 6) = 3∙(х + 1)(х + 3), 3x² + 3x = 0, х = 0; -1Корень х = -1 исключаем. Отв. 0▲3)

---

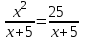
▼ Общий знаменатель х + 5 ≠ 0, х ≠ -5.

x² = 25, х = ±5

Корень х = -5 исключаем. Отв. 5▲

4)

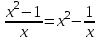
▼ Общий знаменатель х ≠ 0.

x² - 1 = x³ - 1, x³ – x²= 0, x² (x - 1) = 0, х = 0; 1

Корень х = 0 исключаем. Отв. 1▲

5)

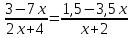
▼ Общий знаменатель 2(х + 2) ≠ 0, х = -2.

3 – 7х = 2(1,5 – 3,5x), 3 – 7х = 3 – 7х, 0 = 0 (истина), х = (-∞; ∞).

Исключая х = -2, получим хϵ(-∞;-2)U(-2; ∞)▲
Уравнения  .

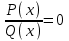
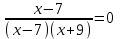
1) 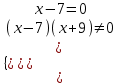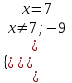 ,  нет корней.

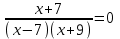
2) 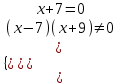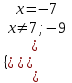 ,  х = -7.

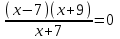
3) 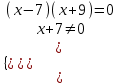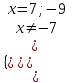 ,  х = 7; -9.

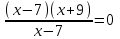
4)  ,  х = -9.

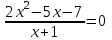
5) 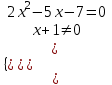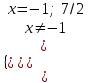 ,  х = 7/2.

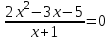
6) 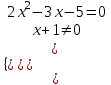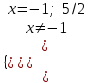 ,  х = 5/2.

Уравнения высших порядков

I. Метод введения новой переменной.

1) x⁴ - 11x² – 12 = 0 – биквадратное уравнение.

x² = t ≥ 0, t² – 11t - 12 = 0, t= -1; 12, t= -1 – исключаем

t= 12, x² = 12, х = ± 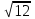= ±2

---

Смотрите также файлы

• Император Акихито родился 23 декабря 1933 года в Токио, Япония. Он был первым сыном Императора Хирохито и Императрицы Нагако. В 1959 году Акихито женился на Мичико Шода, дочери бывшего председателя торговой компании.docx

• Выберите все верные ответы. В каких нормативноправовых документах определена государственная политика в сфере образования в области воспитания и сохранения традиционных для нашего общества ценностей.doc

• Wretched, beastly.doc

• Теоретические аспекты формирования и использования финансовых ресурсов бюджетных организаций.pptx

• Отчет о практическом занятии 1 Тема Установка и настройка по open Server Panel. Цель Установить и настроить по open Server Panel.docx