ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В частности, при М= 0 получаем:
а) Два положительных корня: 0 < х1 х2
a > 0:
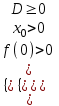; a < 0: 
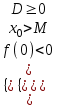; или 
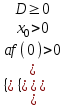
а) Два отрицательных корня: х1 х2 < 0
a > 0:
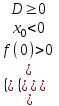; a < 0: 
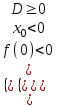; или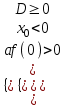 
3) Число М лежит между корнями: х1
a > 0: f(M) < 0; a < 0: f(M) > 0; или af(M) < 0
| a > 0 | a < 0 |
        M x1 x2 |     M x1 x2 |
В частности, при М = 0 получаем корни разных знаков: х1 <0 < х2
a > 0: f(0) < 0; a < 0: f(0) > 0; или af(0) < 0
4) Оба корня лежат в интервале (A; B): A < х1 х2 < B
a > 0:
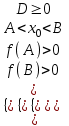; a < 0: 
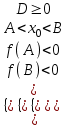; или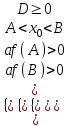 
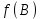  a > 0 | a < 0 |
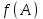      B A x0 x2 x1 |     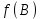A B x2 x0 x1  |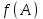
5) Отрезок A; B лежат между корнями: х1 х2
a > 0:
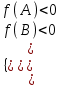; a < 0: 
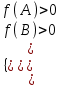; или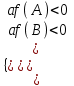 
| a > 0 |  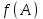a < 0 |
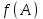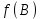   B A x2 x1 | 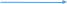   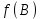A B x2 x1 |
6) Только меньший корень входит в интервал (A; B): A< х1 < B < х2
a > 0:
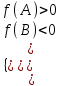; a < 0: 
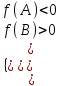; или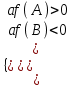 
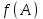| a > 0 |   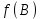a < 0 |
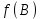| B A x2 x1 |  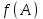B A x2 x1 |
7) Только больший корень входит в интервал (A; B): х1 < A< х2 < B
a > 0:
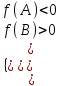; a < 0: 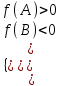; или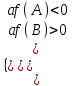 
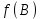| a > 0 | 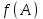a < 0 |
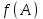| A B x2 x1 |  A 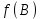B x2 x1 |
Замечание. В условиях задач, как правило, не указывается, что рассматривается именно квадратный трехчлен, поэтому случай а = 0 требует отдельного рассмотрения.
1) При каком значении а оба корня уравнения x2 - аx + 4 = 0 меньше 4.
▼ По условию х1 х2 < 4. Запишем условия, соответствующие задаче
; 
; 
; 
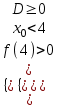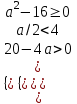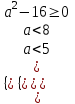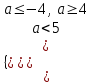. Отв. (-;-44; 5)2) При каких значениях а корни уравнения (а + 1)x2 + 2x - 3а - 1= 0 меньше 1.
▼ По условию х1 х2 < 1.
При а + 1 = 0, а = -1, 2х + 2 = 0, х = -1 < 1 (годится).
При а -1 уравнение квадратное. Решение задачи сводится к решению системы
; 
;
;
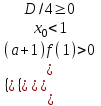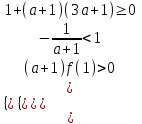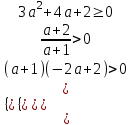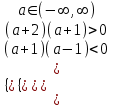
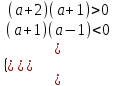-1< a < 1Объединяя результаты с а = -1, получим -1 a < 1. Отв. -1; 1).
3) Найти все значения а, при каждом из которых уравнение
аx2 – 2(а + 1)x + а - 3= 0 имеет отрицательные корни.
▼ По условию х1 х2 < 0.
При а = 0, -2х - 3= 0, х = -3/2 (годится).
При а 0 уравнение квадратное. Решение задачи сводится к решению системы
; 
; 
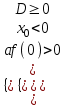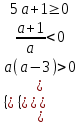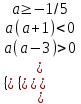-1/5 a < 0Объединяя результаты с а = 0, получим -1 a < 1. Отв. -1/5; 0.
4) При каких значениях а число 4 находится между корнями уравнения
x2 - аx + 4= 0.
▼ По условию х1 <4 < х2. Решение задачи сводится к решению неравенства
f(4) = 16 – 4а + 4 < 0, a > 5. Отв. (5; ).
5) Найти все значения параметра а, при каждом из которых уравнение
(а – 4)x2 – 3аx + а - 2= 0 имеет два корня разных знаков.
▼ По условию х1 <0 < х2, (а – 4) 0, а 4. Решение задачи сводится к решению неравенства
(a – 4)f(0) < 0, (a – 4)(a – 2) < 0, 2 < a < 4. Отв. (2; 4).
6) При каких значениях а оба корня уравнения x2 - аx + 4= 0 заключены в интервале (1; 4).
▼ По условию 1< х1 х2 < 4. Решение задачи сводится к системе
; 
; 
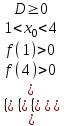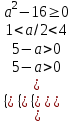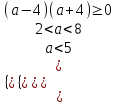4 a < 5. Отв. 4; 5).7) При каких значениях параметра а один из корней уравнения
x2 - 2аx + 2а2 – 4а + 3 = 0 меньше 1, а другой – больше 2.
▼ По условию х1 < 1 < 2 < х2. Решение задачи сводится к системе неравенств
; 
;
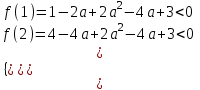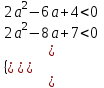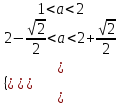
2 -
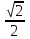< a < 2. Отв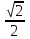. (2 - ; 2). 8) При каких значениях параметра а корни уравнения
(3а + 2)x2 + (а - 1)x + 4а + 3 = 0 удовлетворяют условию х1 < -1 < х2 < 1 (только больший корень входит в интервал (-1; 1)).
▼ Решение задачи сводится к системе неравенств
; 
; 
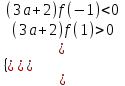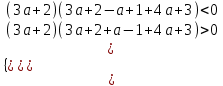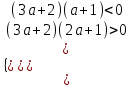-1 < a <-2/3. Отв. (-1;=2/3).0>4>0>
Теорема. Квадратный трехчлен f(x) имеет два корня A1< х1< B1 и A2< х2 < B2, расположенные по одному на каждом из двух непересекающихся интервалов (A1,B1) и (A2,B2) тогда и только тогда, когда одновременно выполняются условия
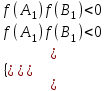
      B1 B2 А2 А1 x2 x1 |
9) При каких значениях параметра а квадратное уравнение
(а - 1)x2 - (а + 1)x + а = 0 имеет два корня, расположенные по одному на каждом из интервалов (0; 1) и (2; 3).
▼ По условию 0 < х1< 1 и 2 < х2< 3. Решение задачи сводится к системе неравенств (см. теорему)
, 
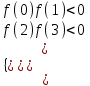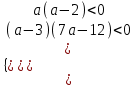12/7 a < 2. Отв. (12/7; 2).Теорема. Квадратный трехчлен f(x) имеет один корень внутри
интервала (A; B), а другой расположен вне этого интервала тогда и только тогда, когда выполняются условие f(A)f(B) < 0.
A < х1< B < х2
B
А
x2
x1
10) При каком значении параметра а квадратное уравнение
(а - 2)x2 - 2(а + 3)x + 4а = 0 имеет один корень внутри интервала (0; 2), а другой расположен вне этого интервала.
▼ По условию 0 < х1< 2 < х2 ; а – 2 0, а 2. Решение задачи сводится к системе неравенств (см. теорему)
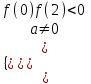, f(0) = 4a, f(2) = 4(a - 2) – 4(a + 3) + 4a = 4(a – 5)
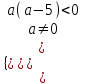a(0; 2)(2; 5). Отв. (0; 2)(2; 5).
Квадратные неравенства с параметрами
Неравенства вида ax2 + bx + c > 0 (<, , ), где a, b, c – выражения, зависящие от параметров, a 0, x – неизвестное, называется квадратным неравенством с параметрами.
Графический метод. При квадратных неравенств используется схематическое изображение функции f(х) = ax2 + bx + c, которая в зависимости от знаков коэффициента а и дискриминанта D имеет следующие расположения относительно оси абсцисс
| a > 0 | D > 0 | D = 0 | D < 0 |
  x1 x2 | x0 | | |
| a < 0 |  x1 x2 | x0 | |
Решение неравенства ax2 + bx + c > 0 () будет числовой промежуток, на котором парабола лежит выше оси абсцисс.
Решение неравенства ax2 + bx + c < 0 () будет числовой промежуток, на котором парабола лежит ниже оси абсцисс.
Если квадратное неравенство нестрогое, то концы промежутка включаются, если строгое, то не включаются
1) Решить неравенство x2 + 2x + а > 0
▼ D = 4 - 4a = 4(1 - a)
Корни x2 + 2x + а = 0: x1 = -1 -
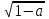, x2 = -1 + 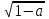, x1 < x2 Рассмотрим три случая в зависимости от знака дискриминанта
а) D > 0, 1 – a > 0, a < 1, х(-;-1 -
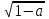)(-1 + ; )
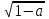б) D = 0, 1 – a = 0, a = 1, x2 + 2x + 1 > 0, (x + 1)2 > 0, х(-;-1)(-1; )
в) D < 0, 1 – a < 0, a > 1, х(-; )
Отв. при a < 1, х(-;-1-
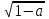)(-1 + 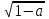; ); при a = 1, х(-;-1)(-1; ); при a > 1, х(-; ).
2) Решить неравенство x2 – (а + 1)x + а 0
▼ D = (а + 1)2 - 4a = (а - 1)2
Корни x2 – (а + 1)x + а = 0: x1 = 1, x2 = а
Рассмотрим три случая в зависимости от знака дискриминанта
а) D > 0, (а - 1)2 > 0, а 1,
при a > 1, x1 = 1 < а = x2, х(-; 1а; )
при a < 1, x2 = а < 1 = x1, х(-; а1; )
б) D = 0, (а - 1)2 = 0, а = 1, x2 - 2x + 1 0, (x - 1)2 0, х(-; )
в) D < 0, (а - 1)2 < 0 (ложь).
Отв. при a < 1, х(-; а1; ); а = 1, х(-; ); при a > 1, х(-; 1а; )
3) Для каждого значения параметра а решить неравенство
аx2 – (2а + 1)x + 2 > 0
▼ При а = 0, -x + 2 > 0, x< 2, x(-; 2)