При а  0 неравенство квадратное

D = (2а + 1)² - 8a = (2а - 1)².

Корни квадратной функции у = аx² – (2а + 1)x + 2: х = 2 или

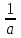
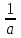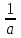При а < 0 ветви параболы направлены вниз, причем а < 0, 2 > , х( ; 2)



При а > 0 ветви параболы направлены вверх, но нельзя однозначно указать, какой корень больше или меньше. Рассмотрим всевозможные варианты

а) 2 = 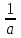, а = 0,5; х(-; 2)(2; )



б) 2 < 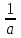, 0 < а < 0,5; х(-; 2)( ; )



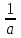в) 2 > 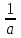, а > 0,5; х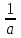(-; )(2; )



Отв. при а < 0,5, х(-; 2)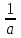( ; ); при а = 0, х(-; 2); при 0 < а < 0,5;

х(-; 2)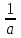( ; ); при а = 0,5; х(-; 2)(2; ); при а > 0,5; х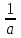(-; )(2; )

4) При всех а решить неравенство

аx² + (а + 1)x + 1  0

▼ При а = 0, x + 1  0, x -1, x(-; -1

При а  0 неравенство квадратное

D = (а + 1)² - 4a = (а - 1)².

Корни квадратной функции у = аx² + (а + 1)x + 1: х = -1 или -

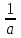
При а < 0 ветви параболы направлены вниз, причем а

---

< 0, -1 < - ,

х(-;-1- ; )

При а > 0 ветви параболы направлены вверх, но нельзя однозначно указать, какой корень больше или меньше. Рассмотрим всевозможные варианты

а) -1 = - , а = 1; х = -1

б) -1 < - , а > 1; х-1;- 

в) -1 > - , 0 < а < 1; х- ;-1

Отв. при а < 0, х(-;-1- ; ); при а = 0, x(-; -1; при 0 < а < 1;

х- ;-1; при а > 1; х-1;- .
Алгоритм решения квадратных неравенств

Вид Неравенства		ax2 + bx + c > 0	ax2 + bx + c  0	ax2 + bx + c < 0	ax2 + bx + c  0
D > 0	a > 0	(-;x1)(x2; )	(-;x1x2; )	(x1; x2)	x1; x2
	a < 0	(x1; x2)	x1; x2	(-;x1)(x2; )	(-;x1x2; )
D = 0	a > 0	(-;x0)(x0; )	(-, )	нет решения	x0
	a < 0	нет решения	x0	(-;x0)(x0; )	(-, )
D < 0	a > 0	(-, )	(-, )	нет решения	нет решения
	a < 0	нет решения	нет решения	(-, )	(-, )

---

Условия, при которых квадратное неравенство выполняется при некоторых ограничениях, приведены в табл.1

Таблица 1

Неравенство	Ограничения на решения
	при всех х	нет решения	единственное	между корнями
ax2 + bx + c > 0		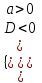	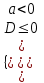не существует		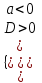(x1; x2)
ax2 + bx + c  0		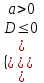		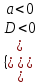	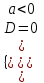x1; x2
ax2 + bx + c < 0		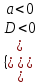	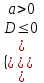не существует		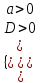(x1; x2)
ax2 + bx + c  0		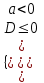		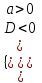	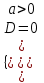x1; x2

Замечание. В условиях задач, как правило, не указывается, что рассматривается именно квадратное неравенство, поэтому случай а = 0 требует отдельного рассмотрения.

1) При каких значениях параметра а неравенство аx² + 4аx + 5  0 не имеет решения.

▼ При а = 0, 5  0 (ложь), нет решения

При а  0 квадратное неравенство.

D = 16a² – 20а = 4а(4а – 5). По табл. 1 выбираем условие

---

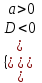
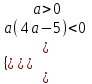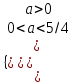; ; , 0 < a < 5/4

Объединяя результаты, получим Отв. 0; 5/4).

2) При каких значениях параметра а неравенство (а - 2)x² – 2х + а - 2 < 0 выполняется при всех х.

▼ При а – 2 = 0, а = 2, -2х < 0, х > 0, х(0; )

При а  2 квадратное неравенство.

D = 4 - 4(а - 2)² = 4(3 - а)(а - 1). По табл. 1 выбираем условие

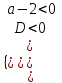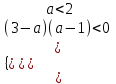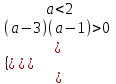; ;  а < 1. Отв. (-; 1).

3) При каких значениях а неравенство аx² + (2 - а)х + 3 - 2а  0 выполняется только для одного действительного х.

▼ При а = 0, 2х + 3  0, х  -3/2, х(-;-3/2 - не подходит условию задачи.

При а  0 квадратное неравенство.

D = (2 - а)² – 4а(3 - 2а) = 9а² - 16а + 1. Чтобы данное неравенство выполнялось только для одного значения х, надо, чтобы ветви параболы были направлены вверх и парабола касалась оси ох (см. табл. 1)

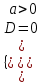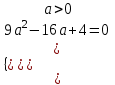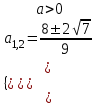; ; ; а = 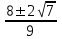. Отв.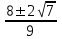

4) При каких значениях параметра а неравенство (х - а)(х – 2)  0 имеет единственное решение.

▼ Контрольные точки х = а и х = 2

При а  0 решением неравенства будет отрезок ха; 2 или х2а; а  (не подходит).

При а = 2, (х – 2)²  0, х = 2 – единственное решение. Отв. 2

5) Для каждого а решить неравенство (х + 15)(х - 3а).

▼ Контрольными точками функции у = (х + 15)(х - 3а) являются х = -15 и

х = 3а. Поскольку однозначно указать, какое из этих чисел больше или меньше, рассмотрим всевозможные варианты

а) -15 = 3а, а = -5 – нет решений;

б) -15 <3а, а > -5; х(-15; 3а)

в) -15 >3а, а < -5; х(3а;-15)

Отв. при а < -5; х(3а;-15); при а = -5 – нет решений; при а > -5; х(-15; 3а)

6) При каком значении параметра а

---

множество решений неравенства

x² + ах – 1 < 0 является интервал длины 5.

▼ Пусть х₁, х₂ – корни квадратного неравенства. По условию х₁ - х₂  = 5,

(х₁ - х₂)² = 25.

, где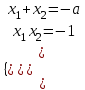

а² + 4 = 25, а² = 21, а =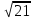 . Отв.  .

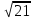7) При каких а неравенство x² + ах + 1 < 0 выполнено для любого

х1; 2.

▼ Требование задачи выполнено, если отрезок 1; 2. Расположен целиком между корнями квадратичной функции f(x) =x² + ах + 1 (см. табл. 1)

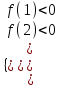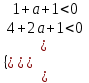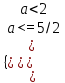; ;  а < -5/2. Отв. а < -5/2.

---

Смотрите также файлы

• Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина История.docx

• Stylistics seminar 1.docx

• Вопросы для подготовки к зачету по дисциплине.doc

• Контрольная работа дисциплина Экономика Вариант 1 Фамилия Березина Имя Екатерина Отчество Сергеевна.docx

• Уравнения с одной переменной.docx