Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc

И даны объемы народного потребления, которые эти экономики должны удовлетворить:

Промышленность	60
Сельское хозяйство	100
Энергетика	80

Определить, которая из экономик эффективнее.

Указание

Эффективность экономик рассчитывается как отношение объемов потребления к общему объему производства по всем отраслям.

13. 
    Для экономики со структурной матрицей, приведенной в табл. 6.5 даны следующие объемы производства по отраслям:
    

Промышленность	80
Сельское хозяйство	40
Энергетика	120

Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.

14. 
    Дана экономика со следующими объемами производства и собственного потребления (в отсутствие народного потребления):
    

	Потребление			Общий выпуск
	Промышленность	Сельское хозяйство	Энергетика
Промышленность	50	16	120	220
Сельское хозяйство	30	10	180	260
Энергетика	15	14	140	350

Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:

Промышленность	60
Сельское хозяйство	70
Энергетика	20

---

15. 
    Дана экономика со следующей структурной матрицей:
    

	Промышленность	Сельское хозяйство	Энергетика
Промышленность	0,20	0,40	0,3
Сельское хозяйство	0,12	0,10	0,10
Энергетика	0,40	0,15	0,20

И даны следующие объемы производства по отраслям:

Промышленность	80
Сельское хозяйство	40
Энергетика	120

Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
6.4. Задача об эквивалентности ставок

---

6.4.1. Основные формулы

В зависимости от условий договора рост вкладов (кредитов, займов, стоимости векселей и оборудования) может быть рассчитан по одной из следующих формул.

По простым процентам, начисляемым один раз в год:

, (6.9)

где S – конечный вклад;

P – начальный вклад;

c₁ – ставка по простым процентам;

t – срок вклада.
По сложным процентам, начисляемым один раз в год:

, (6.10)

где c₂ – ставка по сложным процентам.
По сложным процентам, начисляемым m раз в год:

, (6.11)

где j_m – годовая ставка по сложным процентам, начисляемым m раз в год.

По непрерывным процентам:

, (6.12)

где δ – ставка по непрерывным процентам.
По простой учетной ставке:

, (6.13)

где d_s – простая учетная ставка.
По сложной учетной ставке:

, (6.14)

где d_с – сложная учетная ставка.

По сложной учетной ставке, начисляемой m раз в год:

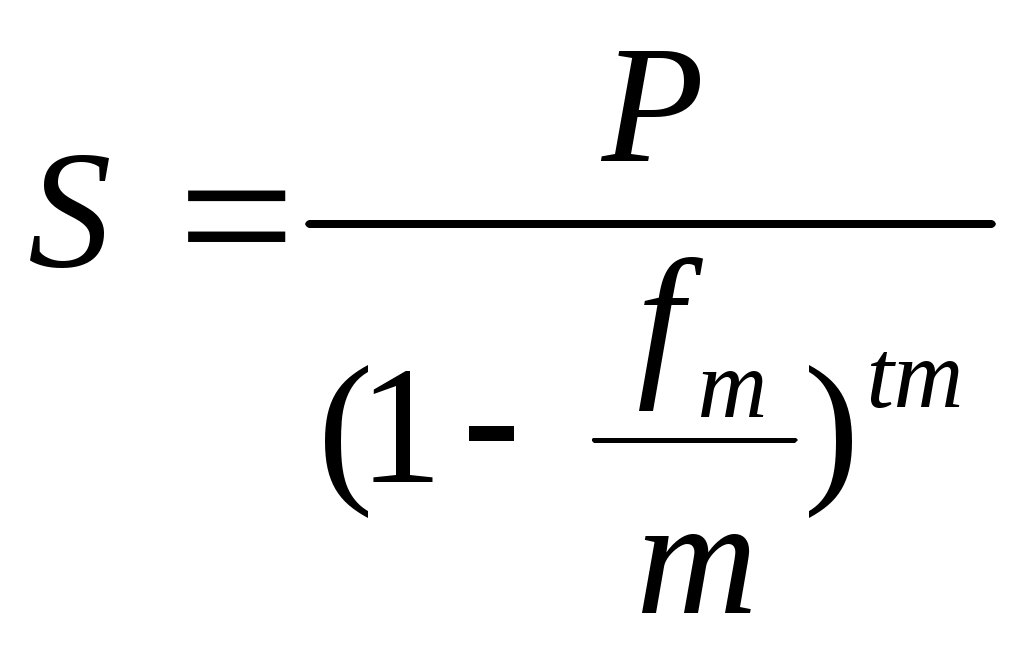, (6.15)

где f_m – сложная учетная ставка.
Амортизация по простым процентам:

, (6.16)

где S₀ – начальная стоимость оборудования;

S₁ – конечная стоимость оборудования;

k₁ – коэффициент амортизации по схеме простых процентов.
Амортизация по сложным процентам:

, (6.17)

где k₂ – коэффициент амортизации по схеме сложных процентов

Во всех формулах время t указано в годах и может быть дробным числом.
6.4.2. Постановка задачи

Задача эквивалентности ставок формулируется следующим образом [1].

---

Предположим, что один банк начисляет проценты по формуле (6.9), а второй – по формуле (6.10). Тогда при одинаковом конечном вкладе эти формулы можно приравнять друг другу.

. (6.18)

Если равны и начальные вклады, то

. (6.19)

В уравнение (6.19) входит три параметра. Зная любые два из них, можно найти и третий. Поэтому возможны три задачи:

а) По известному времени вклада и величине простой ставки найти значение сложной ставки, при которой вклады будут равны.

б) По известному времени вклада и величине сложной ставки найти значение простой ставки, при которой вклады сравняются.

в) По известным значениям простой и сложной ставок найти время, при котором вклады сравняются.

Первые две задачи можно решить с помощью элементарных преобразований.

Например, для второй задачи:

. (6.20)

Однако для третьей задачи это невозможно, т.к. уравнение (6.19) относительно времени аналитически неразрешимо. Поэтому его следует переписать в виде

. (6.21)
и решить относительно t одним из численных методов.

В Excel для этих целей служит средство «Подбор параметра». Математической основой данного средства является один из численных методов решения уравнений.

При использовании любого из этих методов необходимо указание какого–то начального значения корня. При этом начальное значение должно быть как можно ближе к искомому корню. Все это не так существенно, если уравнение имеет один корень. Если же корней несколько, то неопытный пользователь может очень долго подбирать начальные значения.

Все это имеет место в рассматриваемом случае. Здесь уравнение (6.21) имеет два корня, причем первый – тривиальный (при t=0). Второй же корень может быть либо положительным, либо отрицательным – все зависит от соотношения ставок.

Если ставка по простым процентам больше ставки по сложным процентам, то второй (и нужный нам) корень является положительным. Если же имеет место обратная ситуация, то второй корень будет отрицательным.

---

Другими словами для рассматриваемой пары уравнений задача эквивалентности ставок имеет смысл только при c₂ < c₁. В принципе об этом будущим экономистам говорится в соответствующих курсах, но при практическом решении задачи это почему–то забывается.

Поэтому выполнять свои варианты заданий рекомендуется по следующей схеме:

1. 
   Рассчитать таблицу значений функции на выбранном интервале времен и на ее основе построить график функции. По данным таблицы или виду графика определить примерное положение второго корня.
   

Для рассматриваемого примера результат первого этапа приведен в табл. 6.5 и на рис. 6.1. Для получения таблицы в ячейку C6 введена формула:
=1+ $C$2*B6 – (1+$C$3)^B6.
Эта формула затем была скопирована в ячейки C7:C20. Для наглядности по данным ячеек B6:C20 можно построить график – рис. 6.1.

Таблица 6.5.

	A	B	C	D
1
2		Простая ставка	0,05
3		Сложная ставка	0,04
4
5		T	Y
6		0	0
7		1	0,01
8		2	0,0184
9		3	0,025136
10		4	0,030141
11		5	0,033347
12		6	0,034681
13		7	0,034068
14		8	0,031431
15		9	0,026688
16		10	0,019756
17		11	0,010546
18		12	–0,00103
19		13	–0,01507
20		14	–0,03168
21

---