Лаба 1 Задание 1

Задание:

Смоделировать заданную функцию на отрезке [0, 8] с использованием библиотеки neuralnet. Отчет должен содержать подготовку данных для обучения сети. Обоснование выбранной архитектуры. Структурную схему обученной сети с указанием весов. Графики моделируемой и смоделированной функций.

Моделируемая функция

y=0.5*sin(x) + cos(2*x) + sqrt(x)

Ход работы:

Моделируемая функция:

Моделируемая функция, представленная в коде, вычисляется с использованием формулы 0.5*sin(x) + cos(2*x) + sqrt(x). Эта функция комбинирует синус, косинус и квадратный корень от переменной x.

Смоделированная функция

В данном коде нейронная сеть обучается моделировать зависимость между переменными x и y на основе обучающего набора данных. После обучения сети используется функция predict для получения предсказанных значений y на основе нового набора данных.

График, полученный с помощью функции plot(x, y, pch=16, cex=1.5, col='green'), отображает моделируемую функцию. Здесь значения x отображены на оси X, а значения y - на оси Y.

Для смоделированной функции нет явного графика в коде, но с помощью функции points(x, yp, col='black', pch='.', cex=1.5) на график добавляются точки с предсказанными значениями y на основе обученной нейронной сети.

Код программы:

set.seed(9)

x<-runif(50,0,8)

y <- 0.5*sin(x) + cos(2*x) + sqrt(x)

plot(x,y,pch=16,cex=1.5,col='green')

learn=data.frame(x,y)

library(neuralnet)

netcos <- neuralnet (y

x, hidden=4, learn)

set.seed(6)

x<-runif(5000,0,8)

y<-0

test=data.frame(x,y)

yp<-predict(netcos,test)

points(x,yp,col='black',pch='.',cex=1.5)

plot(netcos)

y1=1/(1+exp(-0.44767*x+1.1841))

y2=1/(1+exp(1.59218*x-9.13195))

y3=1/(1+exp(0.61334*x-4.29697) )

y4=1/(1+exp(1.66478*x+4.21321))

set.seed(6)

x <-runif(5000,0,8)

plot(x,y2,col="blue")

points(x,y1,col="red")

points(x,y3,col="green")

points(x,y4,col="yellow")



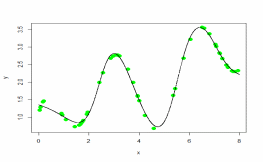
Рисунок 1 - Модель функции 0.5*sin(x) + cos(2*x) + sqrt(x)

Задание 2

Подобрать структуру hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей импульсов. Отчет по работе должен содержать структурную схему обученной сети без указания весов. Графики аппроксимируемой и полученной последовательности для нескольких приближений параметров hidden и threshold.



Программный код:

set.seed(9)

x<-seq(from=-9.5,to =10,by=0.5)

y<-rep(c(1,1,1,1,1,0,0,0,0,0),4)

learn=data.frame(x,y)

library(neuralnet)

netcos<-neuralnet(y x,learn,hidden=c(10,10),threshold = 0.01)

netcos2<-neuralnet (y x,learn,hidden=c(25,20,10),threshold = 0.001)

set.seed(6)

test=data.frame(x,y)

y1<-predict(netcos,test)

y2<-predict(netcos2,test)

par(mfrow = c(3, 2))

plot(x,y,type='l',col='yellow',lwd=9)

lines(x,y1)

plot(x,y,type ='l',col='yellow',lwd=9)

lines (x,y2)



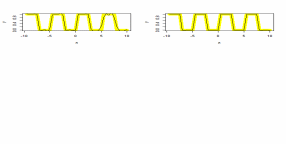
Рисунок 2 - Графики аппроксимируемой и полученной последовательности

Лаба 2

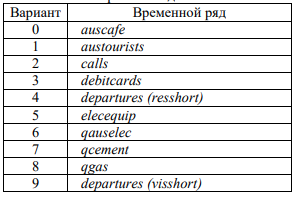
Составить прогноз для заданного временного ряда с использованием библиотеки nnet. Отчет должен содержать подготовку данных для обучения сети. Обоснование выбранной архитектуры. Структурную схему обученной сети без указания весов.



Ход работы

1. 
   Загрузка временного ряда "calls".
   
2. 
   Создание матрицы LearnSeq размером (n-12) x 13, где n - длина временного ряда.
   
3. 
   Заполнение матрицы LearnSeq значениями из временного ряда calls.
   
4. 
   Разделение данных на обучающий и тестовый наборы.
   
5. 
   Обоснование выбранной архитектуры нейронной сети:
   

В данном примере была выбрана нейронная сеть с одним скрытым слоем размером 60 нейронов и линейной функцией активации на выходном слое (linout=TRUE). Эта архитектура была выбрана на основе эмпирического опыта и может потребовать дополнительной настройки для достижения лучшей точности прогнозирования. Размер скрытого слоя (60) можно изменять, исходя из требований конкретного временного ряда.

Код программы:

library(fpp2)

library(nnet)

scripts<-calls

n<-length(scripts)

LearnSeq<-matrix(rep(0, (n-12)*13) ,nrow=n-12,ncol=13)

for(i in 1:(n-12))LearnSeq[i,]<- scripts[i:(12+i)]

set.seed(55)

Nnet<-nnet(LearnSeq[,1:12],LearnSeq[,13],size=60, linout=TRUE, rang=0.1,maxit=300)

prognos <-c(rep(0,12),Nnet$fitted.value)

ggplot(scripts,aes(x))+geom_line(aes(y=scripts),color="blue",size=2)+geom_line(aes(y=prognos),color="yellow",size=0.5)

Визуализация результата:



Лабораторная работа № 4

Построить автокодировщик для заданной обучающей выборки. Отчет должен содержать подготовку данных для обучения сети. Формирование формул для входа и выхода. Визуализацию обучающей выборки и восстановленного образца. Структурную схему обученной сети без указания весов. Варианты заданий приведены в табл., где указаны названия файлов с обучающей выборкой, которые доступны из библиотеки RSNNS



Ход работы:

Загружаем библиотеку RSNNS.

Определяем функцию print.alphabet, которая будет использоваться для визуализации букв.

Загружаем обучающую выборку snnsData$letters_auto.pat из библиотеки RSNNS.

Подготавливаем данные для обучения, создавая датафрейм train.data, который содержит входные и выходные данные.

Формируем формулу form для входа и выхода автокодировщика.

Создаем автокодировщик, используя функцию neuralnet с указанной формулой, обучающими данными, количеством скрытых нейронов и пороговым значением для остановки обучения.

Подготавливаем тестовые данные в датафрейме test.data.

Получаем прогноз от автокодировщика, используя функцию predict.

Визуализируем восстановленные образцы с помощью функции print.alphabet

Код программы:

library(RSNNS)

library(neuralnet)

print.alphabet <- function(x){

letter <- matrixToActMapList(x, nrow = 7)

par(mar = c(1, 1, 1, 1))

par(mfrow = c(4, 7))

n <- c(1:26)

for (i in n) plotActMap(letter[[i]])

}

data(snnsData)

inputs <- snnsData$letters_auto.pat

print.alphabet(inputs)

train.data <- data.frame(inputs, inputs)

x.names <- paste0("in", 1:35, collapse = "+")

y.names <- paste0("out", 1:35, collapse = "+")

form <- as.formula(paste(x.names, " ", y.names))

---

set.seed(55)

net <- neuralnet(formula = form, data = train.data, hidden = 10, threshold = 0.0006)

test.data <- data.frame(inputs)

y.predict <- predict(net, test.data)

print.alphabet(y.predict)



Лабораторная работа № 5

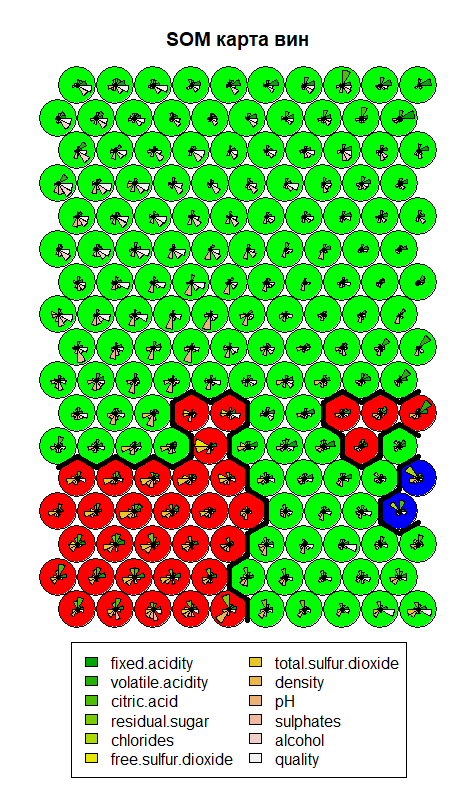
Задание

Построить карты Кохонена для тестовых наборов из ресурса Wine Quality (http://archive.ics.uci.edu/ml/machine-learning-databases/winequality/).



Код программы:

---

Смотрите также файлы

• 2 оценить значимость полученных уравнений на уровне 0,05.docx

• Протокол от " " 2019 г. Е. И. Музычко Согласовано.docx

• Тест фио студента Фам Ван Фу Мань Ответы на тест.docx

• Рабочая программа внеурочной деятельности Робототехника (общеинтеллектуальное направление) 57 класс.docx

• Сптай орта мектебі кмм.docx