Файл: 2 оценить значимость полученных уравнений на уровне 0,05.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 191
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 4
Задание 1.
Имеются данные о выработке литья одного работающего
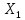 (т), браке литься
(т), браке литься 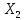 (%), себестоимости одной тонны литься по 20 литейным цехам различных заводов. Необходимо установить связь между себестоимостью и выработкой литья на одного работающего:
(%), себестоимости одной тонны литься по 20 литейным цехам различных заводов. Необходимо установить связь между себестоимостью и выработкой литья на одного работающего: 1) без учета производственного брака (найти уравнение парной регрессии Y (руб.) по
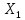 (т));
(т)); 2) оценить значимость полученных уравнений на уровне α=0,05;
3) оценить значимость коэффициента регрессии при
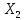 на уровне α=0,05;
на уровне α=0,05;4) получить точечную оценку среднего значения себестоимости 1 т литья в цехах, в которых выработка литья на одного работающего составляет
40 т, а брак литья составляет 5% (данные представлены в табл.1).
Таблица 1 – Исходные данные
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X1i | 44,1 | 83,9 | 44,5 | 83,9 | 76,8 | 83,9 | 80,3 | 83,9 | 83,9 | 67,5 |
| X2i | 1,3 | 7,5 | 8 | 1,3 | 8,6 | 1,3 | 3,5 | 1,3 | 3,4 | 7,5 |
| Yi | 228,6 | 262,7 | 231,5 | 262,7 | 198,6 | 262,7 | 147,6 | 262,7 | 157,9 | 262,7 |
| i | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| X1i | 42,7 | 83,9 | 38,3 | 83,9 | 42,2 | 83,9 | 83,9 | 85 | 42,7 | 83,9 |
| X2i | 3,1 | 1,3 | 3,4 | 1,3 | 7,7 | 1,3 | 5,6 | 2,9 | 3,1 | 1,3 |
| Yi | 143 | 262,7 | 262,7 | 1230,5 | 262,7 | 187,4 | 262,7 | 119,7 | 143 | 262,7 |
Решение:
Общий вид уравнения регрессии:
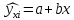
Система нормальных уравнений в общем виде:
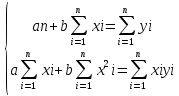
| Приведём расчетную таблицу | |||||||||
| i | Y |  |  | 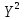 | 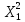 | 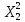 | 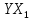 | 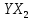 | 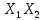 |
| 1 | 228,6 | 44,1 | 6,3 | 52257,96 | 1944,81 | 39,69 | 10081,26 | 1440,18 | 277,83 |
| 2 | 262,7 | 20,5 | 7,5 | 69011,29 | 420,25 | 56,25 | 5385,35 | 1970,25 | 153,75 |
| 3 | 223,9 | 44,5 | 8,0 | 50131,21 | 1980,25 | 64,00 | 9963,55 | 1791,20 | 356,00 |
| 4 | 223,9 | 20,5 | 6,3 | 50131,21 | 420,25 | 39,69 | 4589,95 | 1410,57 | 129,15 |
| 5 | 198,6 | 76,8 | 8,6 | 39441,96 | 5898,24 | 73,96 | 15252,48 | 1707,96 | 660,48 |
| 6 | 223,9 | 20,5 | 6,3 | 50131,21 | 420,25 | 39,69 | 4589,95 | 1410,57 | 129,15 |
| 7 | 147,6 | 80,3 | 3,5 | 21785,76 | 6448,09 | 12,25 | 11852,28 | 516,60 | 281,05 |
| 8 | 223,9 | 20,5 | 6,3 | 50131,21 | 420,25 | 39,69 | 4589,95 | 1410,57 | 129,15 |
| 9 | 157,9 | 20,5 | 3,4 | 24932,41 | 420,25 | 11,56 | 3236,95 | 536,86 | 69,70 |
| 10 | 223,9 | 67,5 | 7,5 | 50131,21 | 4556,25 | 56,25 | 15113,25 | 1679,25 | 506,25 |
| 11 | 213,8 | 67,5 | 8,7 | 45710,44 | 4556,25 | 75,69 | 14431,50 | 1860,06 | 587,25 |
| 12 | 223,9 | 20,5 | 6,3 | 50131,21 | 420,25 | 39,69 | 4589,95 | 1410,57 | 129,15 |
| 13 | 143,0 | 42,7 | 3,1 | 20449,00 | 1823,29 | 9,61 | 6106,10 | 443,30 | 132,37 |
| 14 | 223,9 | 20,5 | 6,3 | 50131,21 | 420,25 | 39,69 | 4589,95 | 1410,57 | 129,15 |
| 15 | 223,9 | 38,3 | 3,4 | 50131,21 | 1466,89 | 11,56 | 8575,37 | 761,26 | 130,22 |
| 16 | 1230,5 | 20,5 | 6,3 | 1514130,25 | 420,25 | 39,69 | 25225,25 | 7752,15 | 129,15 |
| 17 | 223,9 | 42,2 | 7,7 | 50131,21 | 1780,84 | 59,29 | 9448,58 | 1724,03 | 324,94 |
| 18 | 187,4 | 20,5 | 6,3 | 35118,76 | 420,25 | 39,69 | 3841,70 | 1180,62 | 129,15 |
| 19 | 223,9 | 20,5 | 5,6 | 50131,21 | 420,25 | 31,36 | 4589,95 | 1253,84 | 114,80 |
| 20 | 119,7 | 85,0 | 6,3 | 14328,09 | 7225,00 | 39,69 | 10174,50 | 754,11 | 535,50 |
| Сумма | 5128,8 | 793,9 | 123,7 | 2338478,02 | 41882,41 | 818,99 | 176227,82 | 32424,52 | 5034,19 |
| Средн. | 256,44 | 39,70 | 6,19 | 116923,90 | 2094,12 | 40,95 | 8811,39 | 1621,23 | 251,71 |
1 2 3 4 5 6 7 8
Система нормальных уравнений с вычисленными коэффициентами:
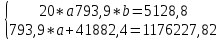
Решение системы:
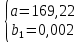
Построенное уравнение регрессии:
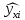 = 169,22+0,002
= 169,22+0,002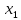
Соответственно, без учета производственного брака при увеличении выработки литья на одного работающего на 1т. себестоимость 1 т. литья увеличивается в среднем на 0,002 руб.
2) Общий вид уравнения регрессии:
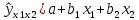
Для нахождения коэффициентов необходимо решить систему:
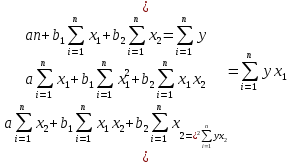
Система уравнений с вычисленными коэффициентами:
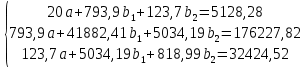
Решение системы:
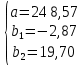
Построенное уравнение регрессии:
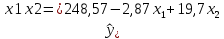
При увеличении выработки литья на одного работающего на 1 т. литья и неизменном проценте брака, себестоимость 1 т. литья увеличивается в среднем на 0,002 руб.
При увеличении брака литья на 1% и неизменной выработке литья себестоимость 1т. увеличится в среднем на 19,7 руб.
| 3) Проведём в таблице расчеты | |||||||||
| i | y | 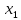 | 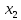 | 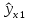 | 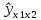 | (y- 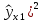 | (y- 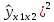 | (y- 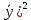 | 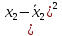 |
| 1 | 228,6 | 44,1 | 6,3 | 196,13 | 246,11 | 1054,18 | 306,71 | 775,07 | 0,01 |
| 2 | 262,7 | 20,5 | 7,5 | 196,18 | 337,49 | 4425,04 | 5592,80 | 39,19 | 1,73 |
| 3 | 223,9 | 44,5 | 8 | 196,13 | 278,46 | 771,12 | 2976,25 | 1058,85 | 3,29 |
| 4 | 223,9 | 20,5 | 6,3 | 196,18 | 313,85 | 768,45 | 8090,10 | 1058,85 | 0,01 |
| 5 | 198,6 | 76,8 | 8,6 | 196,07 | 197,57 | 6,42 | 1,05 | 3345,47 | 5,83 |
| 6 | 223,9 | 20,5 | 6,3 | 196,18 | 313,85 | 768,45 | 8090,10 | 1058,85 | 0,01 |
| 7 | 147,6 | 80,3 | 3,5 | 196,06 | 87,06 | 2348,31 | 3665,21 | 11846,15 | 7,21 |
| 8 | 223,9 | 20,5 | 6,3 | 196,18 | 313,85 | 768,45 | 8090,10 | 1058,85 | 0,01 |
| 9 | 157,9 | 20,5 | 3,4 | 196,18 | 256,72 | 1465,28 | 9764,40 | 9710,13 | 7,76 |
| 10 | 223,9 | 67,5 | 7,5 | 196,09 | 202,60 | 773,67 | 453,90 | 1058,85 | 1,73 |
| 11 | 213,8 | 67,5 | 8,7 | 196,09 | 226,24 | 313,82 | 154,63 | 1818,17 | 6,33 |
| 12 | 223,9 | 20,5 | 6,3 | 196,18 | 313,85 | 768,45 | 8090,10 | 1058,85 | 0,01 |
| 13 | 143 | 42,7 | 3,1 | 196,13 | 187,09 | 2823,29 | 1944,02 | 12868,63 | 9,52 |
| 14 | 223,9 | 20,5 | 6,3 | 196,18 | 313,85 | 768,45 | 8090,10 | 1058,85 | 0,01 |
| 15 | 223,9 | 38,3 | 3,4 | 196,14 | 205,63 | 770,43 | 333,83 | 1058,85 | 7,76 |
| 16 | 1230,5 | 20,5 | 6,3 | 196,18 | 313,85 | 1069819,93 | 840256,39 | 948792,88 | 0,01 |
| 17 | 223,9 | 42,2 | 7,7 | 196,14 | 279,15 | 770,86 | 3052,12 | 1058,85 | 2,30 |
| 18 | 187,4 | 20,5 | 6,3 | 196,18 | 313,85 | 77,07 | 15988,34 | 4766,52 | 0,01 |
| 19 | 223,9 | 20,5 | 5,6 | 196,18 | 300,06 | 768,45 | 5799,58 | 1058,85 | 0,34 |
| 20 | 119,7 | 85 | 6,3 | 196,05 | 128,73 | 5829,32 | 81,54 | 18697,83 | 0,01 |
| | 5128,8 | 793,9 | 123,7 | 3922,81 | 5129,80 | 1095859,48 | 930821,28 | 1023248,55 | 53,91 |
1 2 3 4 5 6 7 8
Коэффициент детерминации определяется по формуле:
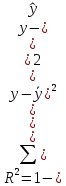
Тогда для первого уравнения:
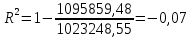
Для второго уравнения:
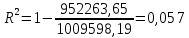
Для определения значимости полученного уравнения регрессии необходимо рассчитать эмпирическую величину F-критерия Фишера:
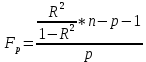
Тогда для первого уравнения:
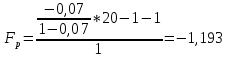
Для второго уравнения:
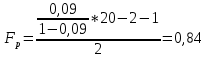
По таблице F-распределения Снедекора-Фишера при α=0,05 и
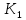 =2,
=2,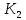 = 20-3=17, величина
= 20-3=17, величина 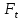 =3,59. При
=3,59. При 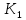 =1,
=1, 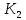 =20-2=18,
=20-2=18, 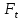 =4,41.
=4,41.Поскольку фактическое значение
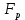
4) На основании данных расчетной таблицы рассчитаем остаточное среднее квадратическое отклонение:
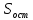 =
=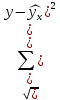 =
= 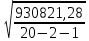 = 233,9
= 233,9Определим стандартную ошибку коэффициента:
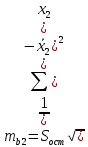 =233,99
=233,99 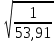 = 0,13
= 0,13Рассчитаем t-статистику:
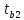 =
= 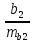 =
=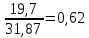
Табличное значение t-критерия Стьюдента при α = 0,05 и k=17 имеет значение
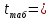 2,11. Таким образом, коэффициент регрессии при
2,11. Таким образом, коэффициент регрессии при  является статистически незначимым на уровне α=0,05.
является статистически незначимым на уровне α=0,05.5) Выполним прогноз:
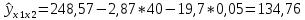 руб/т.
руб/т.Задание 2.
Имеются следующие данные о численности населения США в 1950-1989гг., (млн.чел).
| Год | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 | 1959 |
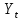 | 152,3 | 153,9 | 157,6 | 159,8 | 165,9 | 166,8 | 172,0 | 174,8 | 177,8 | 180,7 |
| Год | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 |
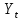 | 181,3 | 186,5 | 187,4 | 189,9 | 191,9 | 193,2 | 194,3 | 196,6 | 197,8 | 198,6 |
| Год | 1970 | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 |
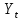 | 200,7 | 201,7 | 203,9 | 205,1 | 207,7 | 209,2 | 209,9 | 210,2 | 211,9 | 213,8 |
| Год | 1980 | 1981 | 1982 | 1983 | 1984 | 1985 | 1986 | 1987 | 1988 | 1989 |
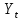 | 216,0 | 218,2 | 220,2 | 222,6 | 225,2 | 227,7 | 230,0 | 232,3 | 236,5 | 237,0 |
Требуется обработать эти данные, выполнив следующие действия:
-
Представить ряд гафически; -
Подобрать подходящее уравнение тренда по методу наименьших квадратов или подходящую скользящую среднюю, если характер тренда неясен; -
Удалить трендовую составляющую из временного ряда и построить график остатков; -
Проанализировать поведение ряда остатков.
Решение:
Построим график
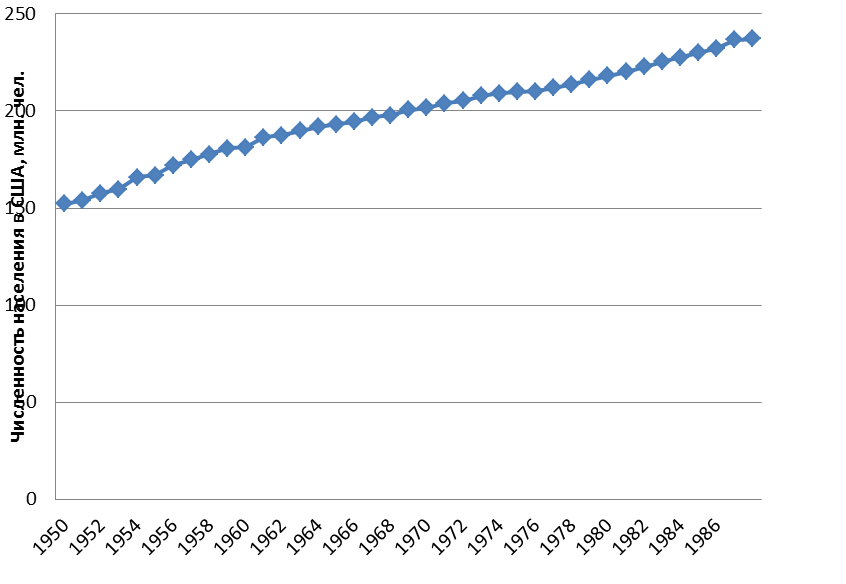
Рисунок 1. – графическое представление ряда данных
2) Так как тренд близок к линейному, построим линейное уравнение тренда. Общий вид уравнения тренда:
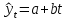
Система нормальных уравнений в общем виде:
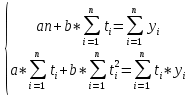
Приведем расчетную таблицу:
| Год | t | y | 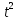 | ty |
| 1950 | 1 | 152,3 | 1 | 152,3 |
| 1951 | 2 | 153,9 | 4 | 307,8 |
| 1952 | 3 | 157,6 | 9 | 472,8 |
| 1953 | 4 | 159,8 | 16 | 639,2 |
| 1954 | 5 | 165,9 | 25 | 829,5 |
| 1955 | 6 | 166,8 | 36 | 1000,8 |
| 1956 | 7 | 172 | 49 | 1204 |
| 1957 | 8 | 174,8 | 64 | 1398,4 |
| 1958 | 9 | 177,8 | 81 | 1600,2 |
| 1959 | 10 | 180,7 | 100 | 1807 |
| 1960 | 11 | 181,3 | 121 | 1994,3 |
| 1961 | 12 | 186,5 | 144 | 2238 |
| 1962 | 13 | 187,4 | 169 | 2436,2 |
| 1963 | 14 | 189,9 | 196 | 2658,6 |
| 1964 | 15 | 191,9 | 225 | 2878,5 |
| 1965 | 16 | 193,2 | 256 | 3091,2 |
| 1966 | 17 | 194,3 | 289 | 3303,1 |
| 1967 | 18 | 196,6 | 324 | 3538,8 |
| 1968 | 19 | 197,8 | 361 | 3758,2 |
| 1969 | 20 | 200,7 | 400 | 4014 |
| 1970 | 21 | 201,7 | 441 | 4235,7 |
| 1971 | 22 | 203,9 | 484 | 4485,8 |
| 1972 | 23 | 205,1 | 529 | 4717,3 |
| 1973 | 24 | 207,7 | 576 | 4984,8 |
| 1974 | 25 | 209,2 | 625 | 5230 |
| 1975 | 26 | 209,9 | 676 | 5457,4 |
| 1976 | 27 | 210,2 | 729 | 5675,4 |
| 1977 | 28 | 211,9 | 784 | 5933,2 |
| 1978 | 29 | 213,8 | 841 | 6200,2 |
| 1979 | 30 | 216 | 900 | 6480 |
| 1980 | 31 | 218,2 | 961 | 6764,2 |
| 1981 | 32 | 220,2 | 1024 | 7046,4 |
| 1982 | 33 | 222,6 | 1089 | 7345,8 |
| 1983 | 34 | 225,2 | 1156 | 7656,8 |
| 1984 | 35 | 227,7 | 1225 | 7969,5 |
| 1985 | 36 | 230 | 1296 | 8280 |
| 1986 | 37 | 232,3 | 1369 | 8595,1 |
| 1987 | 38 | 236,6 | 1444 | 8990,8 |
| 1988 | 39 | 237 | 1521 | 9243 |
| Сумма | 780 | 7720,4 | 20540 | 164614,3 |
1 2 3 4 5 6 7 8
Система нормальных уравнений с вычисленными коэффициентами:
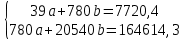
Решение системы:
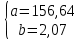
Построенное уравнение тренда:
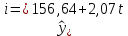
3)Удалим трендовую составляющую из временного ряда:
| Год | t | y | 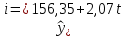 | e = y- 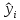 |
| 1950 | 1 | 152,3 | 158,71 | -6,41 |
| 1951 | 2 | 155,7 | 160,78 | -5,08 |
| 1952 | 3 | 157,6 | 162,85 | -5,25 |
| 1953 | 4 | 159,8 | 164,92 | -5,12 |
| 1954 | 5 | 165,9 | 166,99 | -1,09 |
| 1955 | 6 | 166,8 | 169,06 | -2,26 |
| 1956 | 7 | 172 | 171,13 | 0,87 |
| 1957 | 8 | 174,8 | 173,20 | 1,60 |
| 1958 | 9 | 177,8 | 175,27 | 2,53 |
| 1959 | 10 | 180,7 | 177,34 | 3,36 |
| 1960 | 11 | 181,3 | 179,41 | 1,89 |
| 1961 | 12 | 186,5 | 181,48 | 5,02 |
| 1962 | 13 | 187,4 | 183,55 | 3,85 |
| 1963 | 14 | 190,3 | 185,62 | 4,68 |
| 1964 | 15 | 191,9 | 187,69 | 4,21 |
| 1965 | 16 | 193,2 | 189,76 | 3,44 |
| 1966 | 17 | 194,3 | 191,83 | 2,47 |
| 1967 | 18 | 196,6 | 193,90 | 2,70 |
| 1968 | 19 | 197,8 | 195,97 | 1,83 |
| 1969 | 20 | 200,7 | 198,04 | 2,66 |
| 1970 | 21 | 201,7 | 200,11 | 1,59 |
| 1971 | 22 | 203,9 | 202,18 | 1,72 |
| 1972 | 23 | 205,1 | 204,25 | 0,85 |
| 1973 | 24 | 207,7 | 206,32 | 1,38 |
| 1974 | 25 | 209 | 208,39 | 0,61 |
| 1975 | 26 | 209,9 | 210,46 | -0,56 |
| 1976 | 27 | 210,2 | 212,53 | -2,33 |
| 1977 | 28 | 211,9 | 214,60 | -2,70 |
| 1978 | 29 | 213,8 | 216,67 | -2,87 |
| 1979 | 30 | 216 | 218,74 | -2,74 |
| 1980 | 31 | 218,2 | 220,81 | -2,61 |
| 1981 | 32 | 220,2 | 222,88 | -2,68 |
| 1982 | 33 | 222,6 | 224,95 | -2,35 |
| 1983 | 34 | 225,2 | 227,02 | -1,82 |
| 1984 | 35 | 227,7 | 229,09 | -1,39 |
| 1985 | 36 | 230 | 231,16 | -1,16 |
| 1986 | 37 | 232,3 | 233,23 | -0,93 |
| 1987 | 38 | 235,4 | 235,30 | 0,10 |
| 1988 | 39 | 237 | 237,37 | -0,37 |
| Сумма | 780 | 7721,2 | 7723,56 | -2,36 |