ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 55
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лекция 1 Основы математического моделирования
1.2. Основные этапы математического моделирования
Для обсуждения и обоснования основных подходов к разработке проблем математического моделирования технических устройств и процессов в них представляется целесообразным предварительно рассмотреть условную схему (рис. 1.1), определяющую последовательность проведения отдельных этапов общей процедуры вычислительного эксперимента. Исходной позицией этой схемы служит технический объект (ТО), под которым будем понимать конкретное техническое устройство, его агрегат или узел, систему устройств, процесс, явление или отдельную ситуацию в какой-либо системе или устройстве.
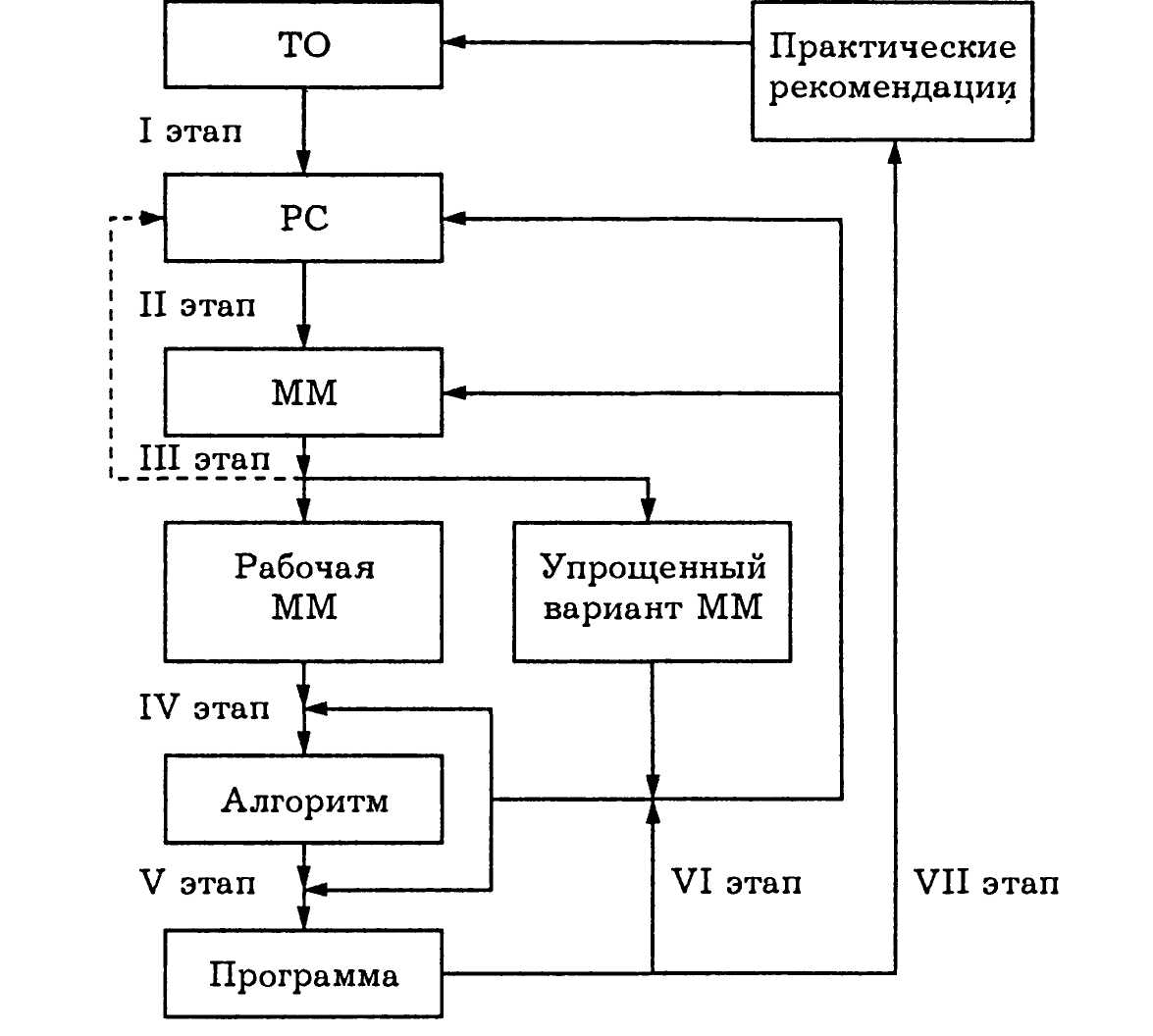
Рис. 1.1
На первом этапе осуществляют неформальный переход от рассматриваемого (разрабатываемого или существующего) ТО к его расчетной схеме (PC). При этом в зависимости от направленности вычислительного эксперимента и его конечной цели акцентируют те свойства, условия работы и особенности ТО, которые вместе с характеризующими их параметрами должны найти отражение в PC, и, наоборот, аргументируют допущения и упрощения, позволяющие не учитывать в PC те качества ТО, влияние которых предполагают в рассматриваемом случае несущественным. Иногда вместо PC используют термин содержательная модель* ТО, а в некоторых случаях — концептуальная модель. В сложившихся инженерных дисциплинах (например, в сопротивлении материалов, электротехнике и электронике) помимо описательной (вербальной) информации для характеристики PC разработаны специальные приемы и символы наглядного графического изображения. По ряду новых направлений развития техники подобная символика находится в стадии формирования.
При разработке новых ТО успешное проведение первого этапа в значительной мере зависит от профессионального уровня инженера, его творческого потенциала и интуиции. Полнота и правильность учета в PC
свойств ТО, существенных с точки зрения поставленной цели исследования, являются основной предпосылкой получения в дальнейшем достоверных резульатов математического моделирования. И наоборот, сильная идеализация ТО ради получения простой PC может обесценить все последующие этапы исследования.
Содержание второго этапа состоит, по существу, в формальном, математическом описании PC. Это описание в виде математических соотношений, устанавливающих связь между параметрами, характеризующими PC TO, и называют математической моделью (ММ).
Надо сказать, что для некоторых типовых PC существуют банки ММ, что упрощает проведение второго этапа. Более того, одна и та же ММ может соответствовать PC из различных предметных областей. Однако при разработке новых ТО часто не удается ограничиться применением типовых PC и отвечающих им уже построенных ММ. Создание новых ММ или модификация существующих должны опираться на достаточно глубокую математическую подготовку и владение математикой как универсальным языком науки.
На третьем этапе проводят качественный и оценочный количественный анализ построенной ММ. При этом могут быть выявлены противоречия, ликвидация которых потребует уточнения или пересмотра PC (штриховая линия на рис. 1.1). Количественные оценки могут дать основания упростить модель, исключив из рассмотрения некоторые параметры, соотношения или их отдельные составляющие, несмотря на то что влияние описываемых ими факторов учтено в PC. В большинстве случаев, принимая дополнительные по отношению к PC допущения, полезно построить такой упрощенный вариант ММ, который позволял бы получить или привлечь известное точное решение. Это решение затем можно использовать для сравнения при тестировании результатов на последующих этапах. В некоторых случаях удается построить несколько ММ для одного и того же ТО, отличающихся различным уровнем упрощения. В этом случае говорят об иерархии ММ (греческое слово
происходит от
— священный и 
— власть и в данном случае означает упорядочение ММ по признаку их сложности и полноты).Построение иерархии ММ связано с различной детализацией свойств изучаемого ТО. Сравнение результатов исследования различных ММ может существенно расширить и обогатить знания об этом ТО. Кроме того, такое сравнение позволяет оценить достоверность результатов последующего вычислительного эксперимента: если более простая ММ правильно отражает некоторые свойства ТО, то результаты исследования этих свойств должны быть близки к результатам, полученным при использовании более полной и сложной ММ.
Итог анализа на рассматриваемом этапе — это обоснованный выбор рабочей ММ ТО, которая подлежит в дальнейшем детальному количественному анализу. Успех в проведении третьего этапа зависит, как правило, от глубины понимания связи отдельных составляющих ММ со свойствами ТО, нашедшими отражение в его PC, что предполагает органическое сочетание владения математикой и инженерными знаниями в конкретной предметной области.
Четвертый этап состоит в обоснованном выборе метода количественного анализа ММ, в разработке эффективного алгоритма вычислительного эксперимента, а пятый этап — в создании работоспособной программы, реализующей этот алгоритм средствами вычислительной техники. Для успешного проведения четвертого этапа необходимо владеть арсеналом современных методов вычислительной математики, а при математическом моделировании довольно сложных ТО выполнение пятого этапа требует профессиональной подготовки в области программирования на ЭВМ.
Получаемые на шестом этапе (в итоге работы программы) результаты вычислений должны прежде всего пройти тестирование путем сопоставления с данными количественного анализа упрощенного варианта ММ рассматриваемого ТО. Тестирование может выявить недочеты как в программе, так и в алгоритме и потребовать доработки программы или же модификации
и алгоритма и программы. Анализ результатов вычислений и их инженерная интерпретация могут вызвать необходимость в корректировке PC и соответствующей ММ. После устранения всех выявленных недочетов триаду „модель — алгоритм — программа" можно использовать в качестве рабочего инструмента для проведения вычислительного эксперимента и выработки на основе получаемой количественной информации практических рекомендаций, направленных на совершенствование ТО, что составляет содержание седьмого, завершающего „технологический цикл" этапа математического моделирования.
Представленная последовательность этапов носит общий и универсальный характер, хотя в некоторых конкретных случаях она может и несколько видоизменяться. Если при разработке ТО можно использовать типовые PC и ММ, то отпадает необходимость в выполнении ряда этапов, а при наличии и соответствующего программного комплекса процесс вычислительного эксперимента становится в значительной степени автоматизированным. Однако математическое моделирование ТО, не имеющих близких прототипов, как правило, связано с проведением всех этапов описанного „технологического цикла".
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Из последовательности основных этапов математического моделирования (см. рис. 1.1) следует, что определяющую роль в нем играет математическая модель (ММ) изучаемого технического объекта. Поэтому прежде всего следует уделить внимание основным свойствам ММ и требованиям к ней, а также классификации ММ.
2.1. Понятие математической модели
Понятие математической модели (ММ), как и ряд других понятий, используемых в математическом моделировании, не имеет строгого формального определения. Тем не менее в это понятие вкладывают вполне конкретное содержание, с которым, в частности, тесно связано применение математики в инженерной практике. Более того, такие научные дисциплины, как механика, физика и их многочисленные разделы, являются, по существу, упорядоченными множествами ММ, построение которых сопровождается теоретическим обоснованием адекватного отражения этими моделями свойств рассматриваемых процессов и явлений. Именно посредством ММ научные дисци
плины взаимодействуют с математикой.
Этапы развития многих естественно-научных направлений в познании законов природы и в совершенствовании техники — это построение последовательности все более точных и более полных ММ изучаемых процессов и явлений. Однако история науки знает не только случаи последовательного уточнения той или иной ММ, но и случаи отказа от некоторых ММ вследствие расхождений прогнозируемых ими результатов с реальностью.
Отвечающая реальности (адекватная) ММ является, как правило, большим научным достижением. Она позволяет провести детальное исследование изучаемого объекта и дать надежный прогноз его поведения в различных условиях. Но за адекватность ММ нередко приходится расплачиваться ее усложнением, что вызывает трудности при ее использовании. В этом случае на помощь математике и приходит современная вычислительная техника, существенно расширившая класс ММ, допускающих исчерпывающий количественный анализ.
Одни и те же ММ находят подчас совершенно различные приложения. Известно, например, что закон Ньютона притяжения двух материальных точек и закон взаимодействия двух точечных электрических зарядов при соответствующем выборе единиц измерения физических величин можно выразить одинаковыми формулами. При помощи одной и той же ММ, содержащей уравнение Пуассона
где
— дифференциальный оператор Лапласа, а 
— искомая и заданная функции положения точки 
некоторой области V, можно изучать установившиеся процессы течения жидкости и распространения теплоты, распределение электрического потенциала, деформацию мембраны, механические напряжения при кручении бруса, фильтрацию нефти в нефтеносном слое или влаги в почве, распространение какой-либо примеси в воздухе или эпидемии в регионе. В каждой из перечисленных задач функции приобретают свой