ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.11.2021
Просмотров: 321
Скачиваний: 2
9
ДОДАТОК 2
ЗАВДАННЯ НА ЕПЮР №1
№ по списку
в журналі
Варіанти завдань
1-6
7-13
14-20
21-30
Група 1
n
перетинає
АС
на відстані 40 мм від точки
С
,
l
||
h
площини.
n
перетинає
АС
в точці, котра ділить відрізок
АС
у
відношенні 1:2,
l
||
f
площини.
n
перетинає
ВС
на відстані 20 мм від точки
В
,
l
паралельна профільній прямій площини.
n
перетинає
ВС
в точці, котра ділить відрізок
ВС
у
відношенні 2:1,
l
||
f
площини.
1-6
7-13
14-20
21-30
Група 2
n
перетинає
АВ
на відстані 30 мм від точки
А
,
l
паралельна лінії скату площини.
n
перетинає площину
АВС
в точці перетину
горизонталі і фронтальні площини,
l
||
АВ
.
n
перетинає площину
ABC
в точці перетину
горизонталі з лінією скату площини,
l
||
ВС
.
n
перетинає
ABC
в точці перетину фронталі з лінією
найбільшого нахилу площини до горизонтальної
площини проекцій,
l
||
АС
.
1-6
7-13
14-20
21-30
Група 3
n
перетинає
АВ
в точці, котра ділить відрізок
АВ
у
відношенні 1:2,
l
паралельна лінії скату площини.
n
перетинає
ВС
на відстані 20 мм від точки
С
,
l
||
h
площини.
n
перетинає площину
ABC
в точці перетину
горизонталі і фронтальні площини,
l
паралельна
профільній прямій площини.
n
перетинає
АС
на відстані 20 мм від точки
А
,
l
||
h
площини.
10
ДОДАТОК 3
ЗАВДАННЯ НА ЕПЮР №2
Дано координати 4-х точок, що не належать одній площині.
Необхідно:
1)
визначити відстань від точки
S
до площини
ABC
(класичним
способом). Скласти алгоритм рішення даної задачі.
№ по списку
в журналі
Варіанти
завдань
1 – 9
2) визначити кут нахилу
ABC
до площини
π
1
;
3) визначити дійсну величину площини
АВС
обертанням
навколо горизонталі площини;
4) визначити двогранний кут при ребрі
SA
методом заміни
площин проекцій;
5) визначити найкоротшу відстань між
SA
і
СВ
методом
заміни площин проекцій;
6) визначити
кут
нахилу
SB
до
АВС
методом
плоскопаралельного переміщення.
10 – 18 2) визначити кут нахилу
ABC
до площини
π
2
;
3) визначити дійсну величину площини
ABC
обертанням
навколо фронталі площини;
4) визначити двогранний кут при ребрі
SB
методом заміни
площин проекцій;
5) визначити найкоротшу відстань між
SB
і
АС
методом
заміни площин проекцій;
6) визначити
кут
нахилу
SВ
до
ABC
методом
плоскопаралельного переміщення.
19 – 30 2) визначити кут нахилу
ABC
до площини
π
1
;
3) визначити дійсну величину площини
ABC
обертанням
навколо горизонтального сліду;
4) визначити двогранний кут при ребрі
SC
методом заміни
площин проекцій;
5) визначити найкоротшу відстань між
SC
і
АВ
методом
заміни площин проекцій;
6) визначити
кут
нахилу
SB
до
АВ
методом
плоскопаралельного переміщення.
11
ДОДАТОК 4
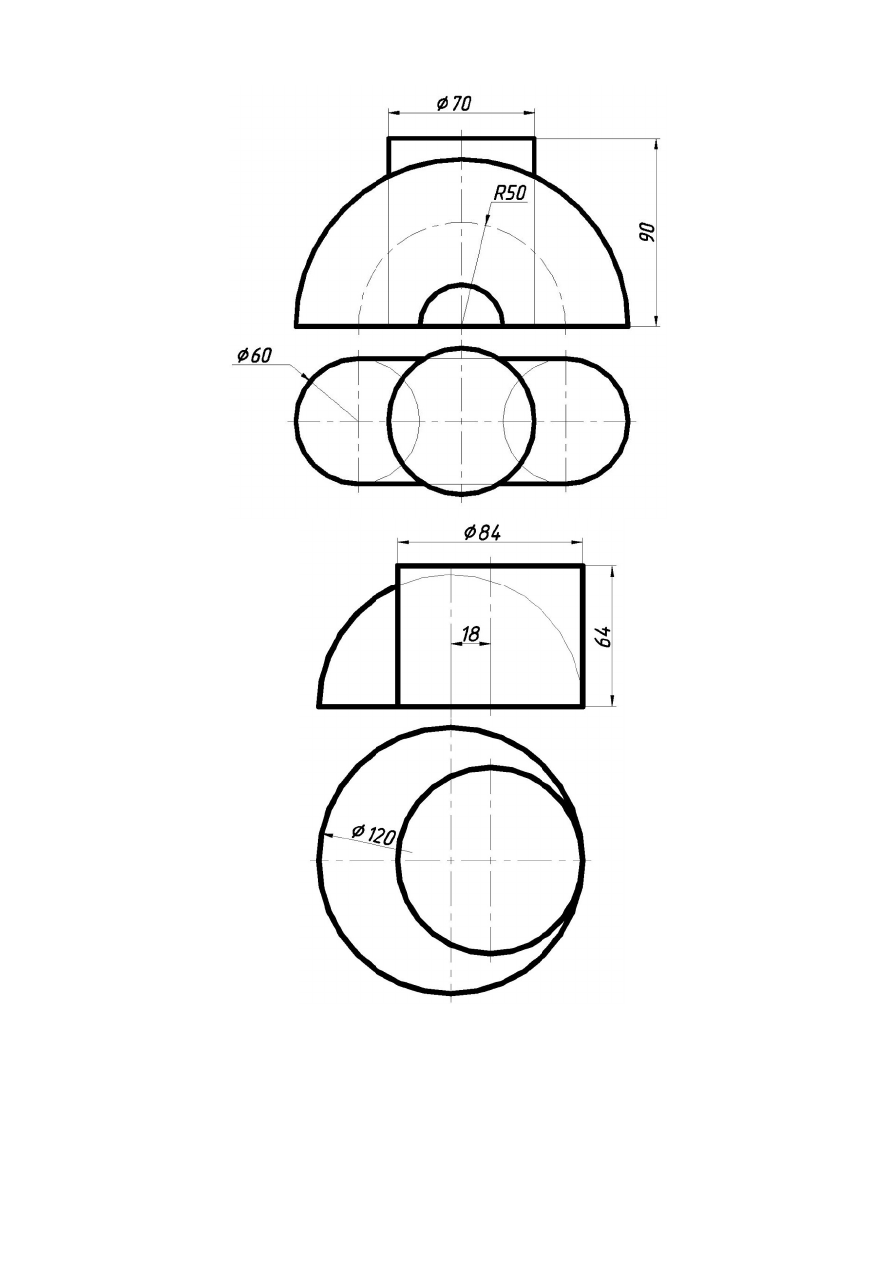
ЗАВДАННЯ НА ЕПЮР №3 (Група 1,2,3)
Дано дві поверхні, що перетинаються.
Необхідно:
1)
побудувати лінію перетину поверхонь, застосовуючи допоміжні
січні площини або допоміжні сфери (по завданню кафедри);
2)
побудувати розгортку однієї із заданих поверхонь із нанесенням
лінії перетину (по завданню кафедри).
12
37
Варіант 1
Варіант 2
13
38
Варіант 3
Варіант 4