Файл: Комплект контрольнооценочных средств оуд. 04 Математика технический и социальноэкономический профиль профессионального образования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 134
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Контрольная работа №3 «Корни и степени» Вариант 1
| Контрольная работа №3 «Корни и степени» Вариант 2
|
Контрольная работа №4 «ЛОГАРИФМЫ»
Вариант 1
1. Вычислите
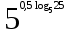 .
.2. Найдите область определения функции у = lg
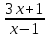 .
.3. Решите уравнения:
а) log2 (4х - 1)= 3;
б) log7 2 = 1- log7 (5 - х).
4. Решите неравенства:
а) log5 (1 - 4х) ≤ 2;
б) log
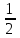 (2х + 3) > -3.
(2х + 3) > -3. Вариант 2
1. Вычислите
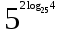 .
.2. Найдите область определения функции у = lg
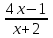 .
.3. Решите уравнения:
а) log4 (2х - 1)= 2;
б) log2 (2х + 3) = log 2 4 + 1.
4. Решите неравенства:

а) log3 (2 - 3х) ≥ 2;
б)
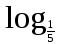 (х + 1) > -2.
(х + 1) > -2. Вариант 3
1. Вычислите
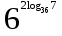 .
.2. Найдите область определения функции у = lg
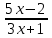 .
.3. Решите уравнения:
а) log5 (6х - 1)= 2;
б) log3 (4х + 5) = log3 9 + 1.
4. Решите неравенства:

а) log4 (2 - 5х) ≥ 3;
б)
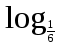 (х - 1) > -1.
(х - 1) > -1. Вариант 4
1. Вычислите
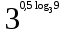 .
.2. Найдите область определения функции у = lg
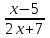 .
.3. Решите уравнения:
а) log3 (7х - 2)= 2;
б) log7 (2х + 5) = log749 + 2.
4. Решите неравенства:

а) log4 (5 - х) ≥ 0;
б)
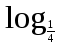 (3х - 1) > - 1 .
(3х - 1) > - 1 . Вариант 5
1. Вычислите
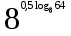 .
.2. Найдите область определения функции у = lg
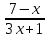 .
.3. Решите уравнения:
а)
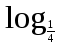 (х - 2)= - 2;
(х - 2)= - 2; б) log5 (2х - 3) = log525 - 2.
4. Решите неравенства:

а) log9 (3 - х) ≤ 0;
б)
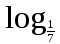 (3х - 1) < - 1 .
(3х - 1) < - 1 . Вариант 6
1. Вычислите
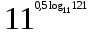 .
.2. Найдите область определения функции у = lg
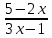 .
.3. Решите уравнения:
а)
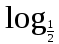 (х - 2)= - 3;
(х - 2)= - 3; б) log8 (2х - 3) = log81 - 1.
4. Решите неравенства:

а) log4 (8 - х) ≤ 2;
б)
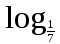 (2х - 1) < 0 .
(2х - 1) < 0 . Вариант 7
1. Вычислите
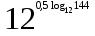 .
.2. Найдите область определения функции у = lg
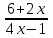 .
.3. Решите уравнения:
а)
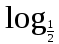 (2х - 1)= - 4;
(2х - 1)= - 4; б) log3 (х - 3) = log327 - 1.
4. Решите неравенства:

а) log5 (5 - х) ≤ 2;
б)
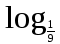 (х + 3) < - 1 .
(х + 3) < - 1 . Вариант 8
1. Вычислите
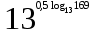 .
.2. Найдите область определения функции у = lg
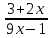
.
3. Решите уравнения:
а)
 (х - 2)= 0;
(х - 2)= 0; б) log3 (х + 9) = log381 - 3.
4. Решите неравенства:

а) log5 (х - 6) ≤ 2;
б)
 (х + 5) > - 2 .
(х + 5) > - 2 . Вариант 9
1. Вычислите
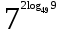 .
.2. Найдите область определения функции у = lg
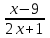 .
.3. Решите уравнения:
а) log8 (5х - 2)= 1;
б) log6 (х + 5) = log6 36 + 1.
4. Решите неравенства:

а) log5 (3 - х) ≥ 0;
Контрольная работа №5«Прямые и плоскости в пространстве»
Вариант 1
-
Что такое стереометрия. -
Какие прямые в пространстве называются параллельными? -
Дана плоскость β и прямые а. в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая а параллельна прямой с, прямые в и с пересекаются, а прямая с лежит в плоскости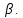 Сделайте рисунок и прокомментируйте его с помощью математических знаков.
Сделайте рисунок и прокомментируйте его с помощью математических знаков. -
Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти длину отрезка ММ1, если АА1=13м, ВВ1=7м, причём отрезок АВ не пересекает плоскость α. -
Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если СС1=21 см, АС : ВС = 3 : 4.
-----------------------------------------------------------------------------------------------------------
Контрольная работа №5«Прямые и плоскости в пространстве»
Вариант 2
-
Назовите основные фигуры в пространстве. -
Какие прямые в пространстве называются скрещивающимися? -
Дана плоскость β и прямые а, в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая в параллельна прямой с, прямые а и в пересекаются, а прямая с лежит в плоскости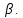 Сделайте рисунок и прокомментируйте его с помощью математических знаков.
Сделайте рисунок и прокомментируйте его с помощью математических знаков. -
Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти длину отрезка ММ1, если АА1=3м, ВВ1=17м, причём отрезок АВ не пересекает плоскость α. -
Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
СС1=26 см, АВ : АС = 15 : 13.
---------------------------------------------------------------------------------------------------------------------------
Контрольная работа №5«Прямые и плоскости в пространстве»
Вариант 3
-
Сформулируйте теорему о трёх точках? -
Что значит: прямая и плоскость параллельны? -
Дана плоскость β и прямые а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежитв плоскости β, прямая в параллельна плоскости β, а прямая с пересекает плоскость β.Сделайте рисунок и прокомментируйте его с помощью математических знаков. -
Через концы отрезка АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1 и М1. Найти длину отрезка ММ1, если отрезок АВ не пересекает плоскость α и если АА1=10м, ВВ1=14м. -
Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
АВ=8 см, АС : СС1 = 2 : 3.
------------------------------------------------------------------------------------------------------------
Контрольная работа №5«Прямые и плоскости в пространстве»
Вариант 4
-
Сформулируйте теорему о прямой и точке. -
Какие плоскости называются параллельными? -
Дана плоскость β и прямые а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежитв плоскости β, а прямые в и с пересекают плоскость β.Сделайте рисунок и прокомментируйте его с помощью математических знаков. -
Через концы отрезка АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1 и М1. Найти длину отрезка ММ1, если отрезок АВ не пересекает плоскость α и если АА1=12м, ВВ1=8м. -
Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
СС1=14 см, АВ : ВС = 10 : 3.
Контрольная работа №7 «Координаты и векторы»
Вариант № 1
-
Сторона равностороннего треугольника равна 12 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью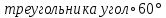
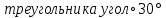 .
. -
Даны точки А(0;0;7), В(1;4;2), С(0;4;5), D(4;2;0). Какие из этих точек лежат:
1) в плоскости ху; 2) на оси z; 3) в плоскости уz.
-
Докажите, что четырёхугольник АВСD с вершинами в точках А(0;2;-3),
В(-1;1;1), С(2;-2;-1), D(3;-1;-5).
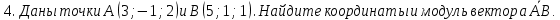
5. Даны точки А(1;-1;3), В(3;-1;1) и С(-1;1;3). Вычислите угол между векторами
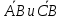 .
.----------------------------------------------------------------------------------------------------
Контрольная работа №7 «Координаты и векторы»
Вариант № 2
-
Дан прямоугольный треугольник с катетами 6 и 9 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью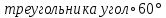 .
. -
Даны точки А(0;6;0), В(0;3;3), С(3;4;8), D(1;0;9). Какие из этих точек лежат:
1) в плоскости хz; 2) на оси у; 3) в плоскости уz.
3. Докажите, что четырёхугольник АВСD с вершинами в точках А(2;1;3),
В(1;0;7), С(-2;1;5), D(-1;2;1).
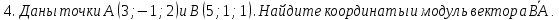
5. Даны точки А(1;3;0), В(2;3;-1) и С(1;2;-1). Вычислите угол между векторами
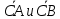 .
.Контрольная работа №7 «Координаты и векторы»
-
Дан прямоугольный треугольник с катетами 6 и 9 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью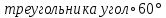 .
. -
Даны точки А(0;6;0), В(0;3;3), С(3;4;8), D(1;0;9). Какие из этих точек лежат:
1) в плоскости хz; 2) на оси
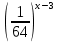 = 23-2х;
= 23-2х;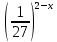 > 92х-1;
> 92х-1;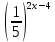 = 1253-4х;
= 1253-4х;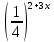 < 8х-1;
< 8х-1;