Файл: Курс лекций по дисциплине Информационные технологии в юридической деятельности.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 519
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
а) в зависимости от числа явлений (переменных):
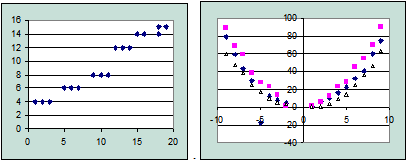
Рис. 4. Линейная зависимость Рис. 5. Нелинейная зависимость
- простой (регрессия между двумя переменными, рис. 4, 5);
- множественной (регрессия между зависимой переменной (y) и несколькими объясняющими ее переменными (х1, х2...хn);
б) в зависимости от формы (см. рис. 9, 10):
- линейной (отображается линейной функцией, а между изучаемыми переменными существуют линейные соотношения);
- нелинейной (отображается нелинейной функцией, между изучаемыми переменными связь носит нелинейный характер);
в) по характеру связи между включенными в рассмотрение переменными:
- положительной (увеличение значения объясняющей переменной приводит к увеличению значения зависимой переменной и наоборот);
- отрицательной (с увеличением значения объясняющей переменной значение объясняемой переменной уменьшается);
г) по типу:
- непосредственной (в этом случае причина оказывает прямое воздействие на следствие, т.е. зависимая и объясняющая переменные связаны непосредственно друг с другом);
- косвенной (объясняющая переменная оказывает опосредованное действие через третью или ряд других переменных на зависимую переменную);
- ложной (нонсенс-регрессия) - может возникнуть при поверхностном и формальном подходе к исследуемым процессам и явлениям. Например, регрессия, устанавливающая связь между уменьшением количества потребляемого алкоголя в нашей стране и уменьшением продажи стирального порошка.
При проведении регрессионного анализа решаются следующие основные задачи:
1. Определение формы зависимости.
2. Определение функции регрессии. Для этого используют математическое уравнение того или иного типа, позволяющее, во-первых, установить общую тенденцию изменения зависимой переменной, а, во-вторых, вычислить влияние объясняющей переменной (или нескольких переменных) на зависимую переменную.
3. Оценка неизвестных значений зависимой переменной. Полученная математическая зависимость (уравнение регрессии) позволяет определять значение зависимой переменной как в пределах интервала заданных значений объясняющих переменных, так и за его пределами. В последнем случае регрессионный анализ выступает в качестве полезного инструмента при прогнозировании изменений социально-экономических процессов и явлений (при условии сохранения существующих тенденций и взаимосвязей). Обычно длина временного отрезка, на который осуществляется прогнозирование, выбирается не более половины интервала времени, на котором проведены наблюдения исходных показателей. Можно осуществить как пассивный прогноз, решая задачу экстраполяции, так и активный, ведя рассуждения по известной схеме «если ..., то» и подставляя различные значения в одну или несколько объясняющих переменных регрессии.
Технология построения регрессии
Для построения регрессии используется метод, получивший название метода наименьших квадратов. Суть его заключается в нахождении по фактическим данным динамического ряда теоретической кривой (тренд), точки которой равноудалены от кривой 1 (см. рис. 6).
При выборе модели регрессии одним из существенных требований к ней является возможность обеспечения наибольшей простоты, позволяющей получить решение с достаточной точностью. Поэтому для установления статистических связей вначале, как правило, рассматривают модель из класса линейных функций, затем другие.
Существует хорошо развитая система подбора аппроксимирующих функций - методика группового учета аргументов (МГУА), достаточно удачно реализованная в программе Excel.
О правильности подобранной модели можно судить по результатам исследования остатков
Модель считается адекватной, если
5. Прогноз, понятие, классификация, методы
5.1 Общие понятия прогнозирования
Прогноз - это научно обоснованное суждение о возможных состояниях объекта в будущем и (или) об альтернативных путях и сроках их достижения.
Под прогнозированием понимают процесс разработки прогнозов. Прогнозы, разрабатываемые в сфере деятельности органов внутренних дел, относятся к категории обществоведческих или юридических. Наиболее характерным видом юридического прогноза является криминологический прогноз.
Под криминологическим прогнозом обычно понимается научное предсказание изменений в структуре и динамике преступности (в целом как явления, отдельных его видов, групп и т.д.) в будущем.
Период упреждения прогноза - промежуток времени от настоящего в будущее, на который разрабатывается прогноз.
Прогнозный горизонт - максимально возможный период упреждения прогноза.
В основе определения периода упреждения лежит общий методологический принцип: прогноз возможен лишь во временных границах, в которых количественные изменения не выходят за пределы данного качества, т.е. пока действуют характерные для данного качества законы. В рамках этих временных границ для юридических прогнозов в соответствии с характером и темпами развития преступности как явления применяется следующая градация прогнозов по периоду упреждения:
-
краткосрочные прогнозы - до одного года; -
среднесрочные прогнозы - от одного до пяти лет;
- долгосрочные прогнозы - на период свыше пяти и примерно до пятнадцати лет;
- дальнесрочные прогнозы - свыше пятнадцати лет.
С периодом упреждения связан и другой вид классификации прогнозов, подразделяющий их на качественные и количественные.
Качественные прогнозы разрабатываются в виде качественных оценок развития объекта: общего описания тенденций и ожидаемого характера изменений, а в самом простом случае - утверждение о возможности или невозможности наступления прогнозируемых событий (например, "возможен рост преступности"или "может наступить стабилизация определенных видов преступления" и т.п.).
Количественные прогнозы представляют собой числовые значения прогнозируемых показателей (например, "число краж превысит миллион")либо количественные оценки вероятностей достижения этих значений.
На практике, как правило, прогнозируются одновременно и качественные и количественные характеристики объекта. Соотношение этих сторон в прогнозе зависит от специфики самого объекта прогноза, целей прогнозирования, периода упреждения и др.
Например, с точки зрения последнего критерия достаточно распространенной является следующая структура прогнозной информации: краткосрочные прогнозы являются преимущественно количественными; среднесрочные - количественно-качественными; долгосрочные - в основном качественными; дальнесрочные - качественными.
5.2 Методы прогнозирования
В зависимости оттого, насколько глубоко были исследованы криминологические процессы (получены ли только динамические ряды, либо исследование проведено на уровне изучения причинно-следственных зависимостей) задача выяснения развития любого явления в будущем может решаться тремя методами:
экспертных оценок, экстраполяции, моделирования.
Метод экспертных оценок. Сущность метода экспертных оценок состоит в том, что в основе прогноза используется мнение специалистов, основанное на профессиональном, научном и практическом опыте.
Сущность метода экспертных оценок состоит в том, что в основе прогноза используется мнение специалистов, основанное на профессиональном, научном и практическом опыте. При этом особенно важно вооружить экспертов качественной и количественной аналитической информацией о состоянии преступности, длительных тенденциях в ее среде, процессах, которые на нее могут повлиять. Оценивая все эти данные, эксперты высказывают свое мнение о возможной картине преступности в будущем.
В зависимости от цели экспертизы используются те или иные методы экспертных оценок. Их можно разбить на два класса: методы коллективной работы экспертной группы и методы получения индивидуального мнения членов экспертной группы. К методам коллективной оценки относятся: «комиссия», «мозговая атака», «суд», «индуцирование психоинтеллектуальной деятельности (ИПИД)», «игровая имитация». Колоссальные по своей эмоционально-психологической нагрузке психоэвристические обсуждения на короткое время мобилизуют все мыслительные резервы участников экспертизы, заставляют их интенсивно думать, познавать всю глубину проблемы.
Наиболее известным методом получения индивидуального мнения членов экспертной группы является метод ДЕЛЬФИ. Работа экспертов по этому методу организована следующим образом. Вначале производится индивидуальный опрос экспертов, при этом эксперты не контактируют друг с другом. Затем производится статистическая обработка индивидуальных экспертных оценок с целью определения усредненного мнения группы, а также крайних оценок. Эта обобщенная информация вместе с аргументами экспертов (без персонификации) в пользу своих суждений сообщается всем экспертам. После ознакомления с этой информацией эксперты могут изменить свои первоначальные оценки, если они сочтут аргументы своих коллег убедительными, либо оставить их без изменения. Процедура повторяется несколько раз и завершается при стабилизации экспертных оценок.
Экспертные оценки для разработки прогнозов, как правило, применяются в следующих случаях:
- в условиях отсутствия представительных и достоверных статистических данных о прогнозируемом объекте;
- в условиях неопределенности среды функционирования объекта, влияния на его развитие факторов внешней среды;
-
в условиях дефицита времени и иных экстремальных ситуациях.
Метод экстраполяции заключается в специальной обработке динамических рядов, которая сводится к нахождению показателей уровней, лежащих за пределами временных интервалов анализируемого динамического ряда. Практически, технология экстраполяции часто заключается в продлении на длину прогнозируемого периода тренда, полученного методом наименьших квадратов (рис. 6). Затем из последней точки продленного тренда опускается перпендикуляр на ось Y. Точка пересечения перпендикуляра с осью Y определяет искомое значение признака.
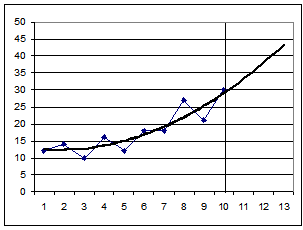
Рис. 6. Прогноз методом экстраполяции.
Следует отметить, что достоверность прогноза методом экстраполяции в большой степени зависит от ряда условий:
1. Факторы, влияющие на динамику исследуемого признака должны быть достаточно стабильны. Например, если разрабатывается прогноз преступности на несколько лет вперед, то должна быть уверенность, что социально-экономические и политические условия не претерпят сильных изменений на прогнозном горизонте.
2. Прогнозный горизонт не должен превышать 1/3 анализируемого периода. Т.е., если необходимо сделать прогноз на три года вперед, то необходимо собрать статистический материал как минимум за последние девять лет.
Ввиду того, что уровни динамического ряда формируются под воздействием множества факторов, а также состоят из нескольких компонент (долговременных, циклических, сезонных и случайных), детальный анализ его поведения представляет собой довольно сложную задачу. Есть и другие особенности прогнозирования динамических рядов области социально-правовых процессов:
- развитие процессов в сфере правопорядка происходит непрерывно, однако характеризующие их уровни динамического ряда соответствуют определенным дискретным моментам времени (месяц, квартал, год), что приводит в некоторых случаях к потере части важной информации;
- динамические ряды представлены часто сравнительно небольшим числом элементов, что затрудняет формальное применение экстраполяционных методов прогнозирования;