Файл: Курс лекций по дисциплине Информационные технологии в юридической деятельности.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 515
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
вычисляется путем деления объема признака на число выделенных его единиц, обладающих таким признаком.
Аср = (А1 + А2 +...+ An)/n ,
где: n - количество выделенных единиц, обладающих общим признаком.
Вариацией признаков называются различия в численных значениях элементов, составляющих совокупность явлений.
Вычисление показателей вариации признаков служит хорошим дополнением к анализу, осуществляемому посредством средних величин, поскольку последние дают лишь общую картину изучаемого явления, не вскрывая их внутреннего содержания и степень однородности выборки.
Простейшим показателем вариации является вариационный размах.
Вариационный размах представляет собой разность между максимальным и минимальным значением признака в выборке:
R = XMAX – XMIN .
Используется только для грубой оценки колеблемости признаков.
4. Выявление тенденций и взаимосвязей в совокупности собранных фактов
4.1 Статистический анализ динамических рядов
Группировка первичного материала и вычисление обобщающих показателей позволяют определить особенности проявления исследуемых социальных процессов. Задача эффективного управления этими процессами требует анализа показателей во времени и взаимосвязи. Для отражения временного развития явления строятся динамические ряды. Они представляют собой совокупности последовательно расположенных показателей, характеризующих изменение какого-либо явления во времени (например, изменение численности населения за некоторый временной интервал – табл. 3).
Простейшими характеристиками динамического ряда являются: уровни ряда, абсолютный прирост, средний уровень ряда, темп роста, средний темп роста, темп прироста.
Числовые значения показателей динамического ряда называются уровнем ряда.
Абсолютным приростом называется разность между каким-то уровнем ряда и предыдущим уровнем или уровнем, принятым за базисный.
Таблица 3
Численность населения Индустриального района (тыс. чел.)
Темп роста (коэффициент роста) показывает во сколько раз уровень данного периода больше или меньше предыдущего или базисного. Различают цепной способ и базисный.
Средний темп роста рассчитывается путем определения средней геометрической величины, т.е. перемножением коэффициентов роста и извлечения из этого произведения корня в степени, равной количеству коэффициентов.
Рср = .
.
Темп прироста – это относительный показатель того, на сколько процентов один уровень больше или меньше другого.
4.2 Выявление тенденций динамических рядов
Задача выявления тенденций в изменении уровней ряда решается путем применения методов выравнивания динамических рядов, которые можно разделить на эмпирические и аналитические.
К эмпирическим методам относят метод укрупнения интервалов и метод скользящей средней.
Суть способа укрупнения интервалов состоит в выборе укрупненного интервала, в пределах которого суммируются показатели уровней имеющегося ряда. Вновь полученные уровни образуют выравненный динамический ряд. Если такое преобразование сразу не приводит к выравниванию ряда, то тогда укрупняют интервал еще раз и т.д.
Для примера рассмотрим условный динамический ряд, характеризующий количество зарегистрированных преступлений по месяцам (см. табл. 4). Для выравнивания ряда выбираем интервал в 3 месяца и в пределах этого интервала суммируем уровни фактического ряда и получаем новый выравненный динамический ряд (см. табл.5).
Таблица 4
Количество преступлений по месяцам
Для выравнивания динамических рядов используется и метод скользящей средней величины. Его суть заключается в замене фактических показателей уровней ряда скользящими средними величинами, взятыми в пределах последовательно скользящего интервала.
Таблица 5
Количество преступлений по кварталам
При этом способе по каждому укрупненному интервалу берется средняя арифметическая фактических уровней, а интервал, начиная с первого, каждый раз переносится на один «шаг» вправо.
Рассмотрим использование метода скользящей средней для выравнивания динамического ряда коэффициента интенсивности (уровня) разбоев по России на 100 тыс. населения (см. табл. 6).
Таблица 6
Динамика уровня разбоев по России
Принимаем укрупненный интервал в три года и в его пределах вычисляем среднюю арифметическую уровней:
6,3 + 3,8 + 5,5
 = 5,2 .
= 5,2 .
3
Сдвигаем интервал на один «шаг» и вычисляем среднюю арифметическую для следующих трех месяцев:
3,8 + 5,5 + 9,9
 = 6,4 .
= 6,4 .
3
В результате последующих аналогичных вычислений получаем выровненный ряд: 5,2; 6,4; 8,9; 11,2; 14,8; 20,1; 24,5.
Сущность аналитических способов выравнивания динамических рядов состоит в том, что, используя математические формулы, находят расчетные уровни рядов динамики, близких к фактическим и выявляющие тенденции развития изучаемого явления к настоящему моменту. Чаще всего здесь используют метод наименьших квадратов (рис.1).
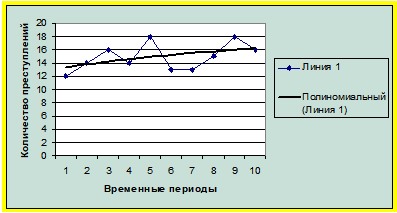
Рис. 1. Получение тренда методом наименьших квадратов
Суть его заключается в нахождении по фактическим данным динамического ряда (линия 1) такой теоретической кривой (в данном случае полиномиальной), точки которой равноудалены от линии 1.
Полученная расчетная кривая отражает длительную тенденцию изменения каких либо показателей, носит название тренда (англ. trend - тенденция) и является основой для дальнейшего прогнозирования изучаемого явления.
4.3 Выявление взаимосвязей в социальных процессах
Вычисление линии тренда, отражающей тенденцию преступности, является базой для разработки прогноза. Но прогнозирование как бы «сам из себя» без учета влияния внешних факторов может привести к достаточно серьезной ошибке. Особенно это касается нестабильных систем, где причинно-следственные зависимости быстро меняются не только по форме и силе, но иногда и по направлению.
Поэтому необходимо идти от исследования преступности в ее «чистом» виде к исследованию тех явлений, процессов и факторов, которые влияют на нее. Главным центральным вопросом при этом выступает не только определение и изучение таких факторов, но и расчет силы их влияния на преступность. Для исследования зависимостей между анализируемыми признаками обычно используют методы корреляционного и регрессионного анализов.
При стохастической (вероятностной) зависимости конкретному значению зависимой переменной соответствует набор значений объясняющей переменной. Это связано, прежде всего, с тем, что на зависимую переменную оказывает влияние ряд неучтенных факторов. Кроме того, сказываются ошибки измерения переменных: вследствие случайного разброса их значения могут быть указаны лишь с определенной вероятностью.
В социально-экономической сфере приходится сталкиваться со многими явлениями, имеющими вероятностную природу. Так, число совершенных и раскрытых преступлений за фиксированный отрезок времени, число дорожно-транспортных происшествий в каком-либо регионе за определенное время - все это случайные величины. Для изучения стохастических взаимосвязей существуют специальные методы, в частности, корреляционный анализ («корреляция» - соотношение, связь между имеющимися явлениями и процессами).
Статистической (стохастической) зависимостью величины Y от нескольких переменных x1, x2, ..., хn называется связь, в соответствии с которой при изменением значения факторных переменных x1, x2, ..., хn результативная переменная Y может принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону. Статистическая связь между различными показателями предполагает, что каждый из них имеет случайную вариацию индивидуальных значений относительно средней величины.
Корреляционной связью двух переменных называют частный случай статистической связи, состоящий в том, что разным значениям факторной переменной X соответствуют различные средние значения результативной переменной Y. Слово «корреляция» ввел в употребление Ф.Гальтон в конце XIXв. обозначая им соответствие (correlation), в отличие от обычной функциональной связи (relation).
Если рассматривается взаимосвязь двух переменных, в которой случайную вариацию имеет лишь один из признаков
Аср = (А1 + А2 +...+ An)/n ,
где: n - количество выделенных единиц, обладающих общим признаком.
Вариацией признаков называются различия в численных значениях элементов, составляющих совокупность явлений.
Вычисление показателей вариации признаков служит хорошим дополнением к анализу, осуществляемому посредством средних величин, поскольку последние дают лишь общую картину изучаемого явления, не вскрывая их внутреннего содержания и степень однородности выборки.
Простейшим показателем вариации является вариационный размах.
Вариационный размах представляет собой разность между максимальным и минимальным значением признака в выборке:
R = XMAX – XMIN .
Используется только для грубой оценки колеблемости признаков.
4. Выявление тенденций и взаимосвязей в совокупности собранных фактов
4.1 Статистический анализ динамических рядов
Группировка первичного материала и вычисление обобщающих показателей позволяют определить особенности проявления исследуемых социальных процессов. Задача эффективного управления этими процессами требует анализа показателей во времени и взаимосвязи. Для отражения временного развития явления строятся динамические ряды. Они представляют собой совокупности последовательно расположенных показателей, характеризующих изменение какого-либо явления во времени (например, изменение численности населения за некоторый временной интервал – табл. 3).
Простейшими характеристиками динамического ряда являются: уровни ряда, абсолютный прирост, средний уровень ряда, темп роста, средний темп роста, темп прироста.
Числовые значения показателей динамического ряда называются уровнем ряда.
Абсолютным приростом называется разность между каким-то уровнем ряда и предыдущим уровнем или уровнем, принятым за базисный.
Таблица 3
Численность населения Индустриального района (тыс. чел.)
Годы | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 |
ЧисленностьНаселения | 244 | 243 | 240 | 235 | 236 | 234 |
Темп роста (коэффициент роста) показывает во сколько раз уровень данного периода больше или меньше предыдущего или базисного. Различают цепной способ и базисный.
Средний темп роста рассчитывается путем определения средней геометрической величины, т.е. перемножением коэффициентов роста и извлечения из этого произведения корня в степени, равной количеству коэффициентов.
Рср =
Темп прироста – это относительный показатель того, на сколько процентов один уровень больше или меньше другого.
4.2 Выявление тенденций динамических рядов
Задача выявления тенденций в изменении уровней ряда решается путем применения методов выравнивания динамических рядов, которые можно разделить на эмпирические и аналитические.
К эмпирическим методам относят метод укрупнения интервалов и метод скользящей средней.
Суть способа укрупнения интервалов состоит в выборе укрупненного интервала, в пределах которого суммируются показатели уровней имеющегося ряда. Вновь полученные уровни образуют выравненный динамический ряд. Если такое преобразование сразу не приводит к выравниванию ряда, то тогда укрупняют интервал еще раз и т.д.
Для примера рассмотрим условный динамический ряд, характеризующий количество зарегистрированных преступлений по месяцам (см. табл. 4). Для выравнивания ряда выбираем интервал в 3 месяца и в пределах этого интервала суммируем уровни фактического ряда и получаем новый выравненный динамический ряд (см. табл.5).
Таблица 4
Количество преступлений по месяцам
ПРИЗНАК | Месяцы | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Количество преступлений | 125 | 114 | 131 | 127 | 111 | 133 | 127 | 117 | 144 | 131 | 128 | 136 |
Для выравнивания динамических рядов используется и метод скользящей средней величины. Его суть заключается в замене фактических показателей уровней ряда скользящими средними величинами, взятыми в пределах последовательно скользящего интервала.
Таблица 5
Количество преступлений по кварталам
| I | II | III | IV |
| 370 | 371 | 388 | 395 |
При этом способе по каждому укрупненному интервалу берется средняя арифметическая фактических уровней, а интервал, начиная с первого, каждый раз переносится на один «шаг» вправо.
Рассмотрим использование метода скользящей средней для выравнивания динамического ряда коэффициента интенсивности (уровня) разбоев по России на 100 тыс. населения (см. табл. 6).
Таблица 6
Динамика уровня разбоев по России
| Годы | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 |
| Уровень Разбоев | 6,3 | 3,8 | 5,5 | 9,9 | 11,3 | 12,4 | 20,7 | 27,2 | 25,6 |
Принимаем укрупненный интервал в три года и в его пределах вычисляем среднюю арифметическую уровней:
6,3 + 3,8 + 5,5
 = 5,2 .
= 5,2 .3
Сдвигаем интервал на один «шаг» и вычисляем среднюю арифметическую для следующих трех месяцев:
3,8 + 5,5 + 9,9
 = 6,4 .
= 6,4 .3
В результате последующих аналогичных вычислений получаем выровненный ряд: 5,2; 6,4; 8,9; 11,2; 14,8; 20,1; 24,5.
Сущность аналитических способов выравнивания динамических рядов состоит в том, что, используя математические формулы, находят расчетные уровни рядов динамики, близких к фактическим и выявляющие тенденции развития изучаемого явления к настоящему моменту. Чаще всего здесь используют метод наименьших квадратов (рис.1).

Рис. 1. Получение тренда методом наименьших квадратов
Суть его заключается в нахождении по фактическим данным динамического ряда (линия 1) такой теоретической кривой (в данном случае полиномиальной), точки которой равноудалены от линии 1.
Полученная расчетная кривая отражает длительную тенденцию изменения каких либо показателей, носит название тренда (англ. trend - тенденция) и является основой для дальнейшего прогнозирования изучаемого явления.
4.3 Выявление взаимосвязей в социальных процессах
Вычисление линии тренда, отражающей тенденцию преступности, является базой для разработки прогноза. Но прогнозирование как бы «сам из себя» без учета влияния внешних факторов может привести к достаточно серьезной ошибке. Особенно это касается нестабильных систем, где причинно-следственные зависимости быстро меняются не только по форме и силе, но иногда и по направлению.
Поэтому необходимо идти от исследования преступности в ее «чистом» виде к исследованию тех явлений, процессов и факторов, которые влияют на нее. Главным центральным вопросом при этом выступает не только определение и изучение таких факторов, но и расчет силы их влияния на преступность. Для исследования зависимостей между анализируемыми признаками обычно используют методы корреляционного и регрессионного анализов.
Корреляционный анализ
Между социально-экономическими явлениями и процессами возможны два вида зависимости: функциональная и стохастическая. При функциональной зависимости имеется однозначное соответствие тех или иных параметров, характеризующих различные явления. Примеры такого рода зависимостей в социальной среде практически не встречаются.При стохастической (вероятностной) зависимости конкретному значению зависимой переменной соответствует набор значений объясняющей переменной. Это связано, прежде всего, с тем, что на зависимую переменную оказывает влияние ряд неучтенных факторов. Кроме того, сказываются ошибки измерения переменных: вследствие случайного разброса их значения могут быть указаны лишь с определенной вероятностью.
В социально-экономической сфере приходится сталкиваться со многими явлениями, имеющими вероятностную природу. Так, число совершенных и раскрытых преступлений за фиксированный отрезок времени, число дорожно-транспортных происшествий в каком-либо регионе за определенное время - все это случайные величины. Для изучения стохастических взаимосвязей существуют специальные методы, в частности, корреляционный анализ («корреляция» - соотношение, связь между имеющимися явлениями и процессами).
Статистической (стохастической) зависимостью величины Y от нескольких переменных x1, x2, ..., хn называется связь, в соответствии с которой при изменением значения факторных переменных x1, x2, ..., хn результативная переменная Y может принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону. Статистическая связь между различными показателями предполагает, что каждый из них имеет случайную вариацию индивидуальных значений относительно средней величины.
Корреляционной связью двух переменных называют частный случай статистической связи, состоящий в том, что разным значениям факторной переменной X соответствуют различные средние значения результативной переменной Y. Слово «корреляция» ввел в употребление Ф.Гальтон в конце XIXв. обозначая им соответствие (correlation), в отличие от обычной функциональной связи (relation).
Если рассматривается взаимосвязь двух переменных, в которой случайную вариацию имеет лишь один из признаков