Добавлен: 09.11.2023
Просмотров: 252
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
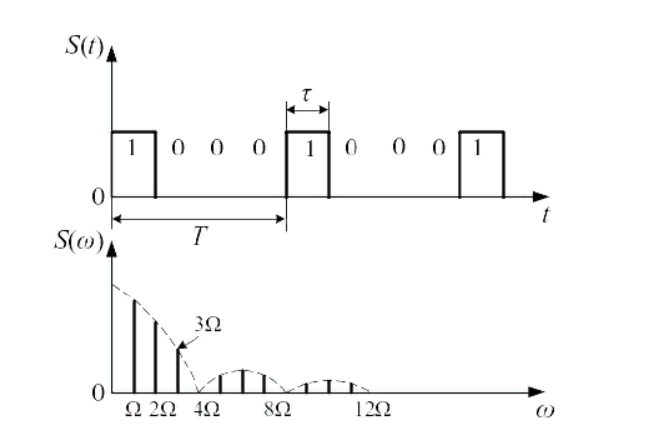
Рис.3- Прямоугольные импульсы со скважностью 2 для приемника ОФМ
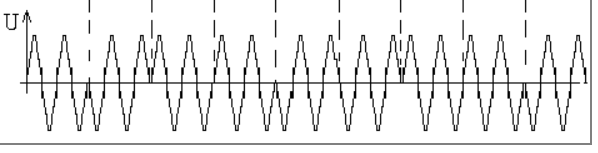
Рис.4 сигнал ОФМ.
РАСЧЕТ ВЕРОЯТНОСТИ ОШИБКИ НА ВЫХОДЕ ПРИЕМНИКА.
Вероятность ошибки в системе передачи д.б. минимально возможной и будет характеризовать потенциальную помехоустойчивость при данном способе модуляции.
Потенциальная помехоустойчивость определена Котельниковым в условиях гауссовских помех. Согласно теории потенциальной помехоустойчивости, любая система передачи информации с заданным ансамблем сигналов в условиях конкретных помех имеет предельную помехоустойчивость, которая не может быть улучшена путем совершенствования приемника, и поэтому называется потенциальной помехоустойчивостью.
Помехоустойчивость приемника определяется вероятность ошибки, зависящая от вида модуляции и способе приёма, и имеет формулу, при заданном отношение сигнал/шум:
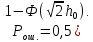
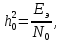
где, Еэ- эквивалентная энергия разности S1(t)-S2(t),
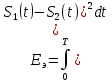
где N0- спектральная плотность мощности помехи; N0=0,001 мкВт/Гц=10 -9 Вт/Гц.
Вероятность ошибки при ОФМ и некогерентном приёма определяется по формуле:
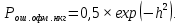
где, h2- отношение средней мощности сигнала к средней мощности помехи; 
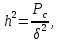
где Pc- мощность сигнала на входе демодулятора приемника; Pc =1,1 мВт=1,1×10-3 Вт.
δ2- дисперсия помехи, находится по формуле:
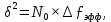
∆ƒэфф- эффективная полоса пропускания канала связи.
Для импульсов постоянного тока прямоугольной формы:
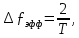
где Т-длительность импульсов: Т=12,0 мкс=12×10-6 с.
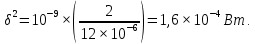
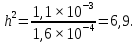
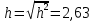
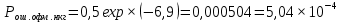
Рассчитаем и построим зависимость вероятности ошибки от мощности сигнала при передаче сигналов ОФМ. Мощность сигнала будем изменять от 0 до такого значения, при котором получается настолько малая вероятность ошибки, что имеющихся таблиц не хватает для ее нахождения.
Результаты расчетов представим в таблице.
Таблица 1 расчётов
По данным таблицы строим график рош=ƒ(Рс) (рис.5), без учета помезоустойчивого или статистического кодирования.
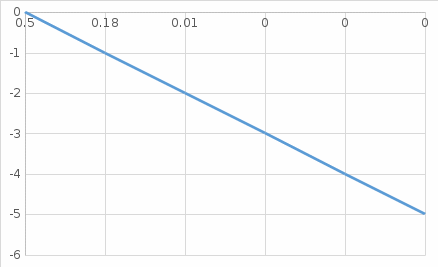
Рис.5- график рош=ƒ(Рс)
ГЛАВА 4 СРАВНЕНИЕ ВЫБРАННОЙ СХЕМЫ ПРИЕМНИКА С ОПТИМАЛЬНЫМ ПРИЕМНИКОМ.4.1 Оптимальный приемник
Оптимальный приемник-это такой приемник, который обеспечивает максимальную помехоустойчивость при данном способе передаче (данном виде сигналов) и данном виде помех.
Следующие виды приемника:
- оптимальный приемник полностью известных сигналов, обеспечивает максимально возможную (потенциальную) помехоустойчивость (приемник Котельникова, или «идеальный приемник»);
- оптимальный приемник неполностью известных сигналов, когда приемник использует не все параметры сигнала, например, не учитывает фазу несущего колебания;
Потенциальная помехоустойчивость достигается благодаря тому, что при приеме учитываются все параметры сигнала, не несущие информации: амплитуда, частота, фаза несущего колебания, а также длительность сигнала Т, т.к. интегрирование (фильтрация) осуществляется в течение этого времени. Решение о принятом сигнале обычно осуществляется в конце каждого интервала Т, для чего в приемнике должна иметься специальная система синхронизации элементов сигнала.
Алгоритм работы оптимального приемника:
Оптимальный приемник полностью известных сигналов используется все параметры сигнала, не несущие информацию.
Рассмотрим систем у передачи информации, в которой передаются два сигнала S
1(t) и S2(t) одинаковой длительности T, произвольный (но известной) формы, априорные вероятности p(S1) и p(S2); помехи в канале связи флуктуационные, ФВП которых имеет вид гауссовского закона
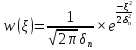
δn2- дисперсия(мощность) помех.
Задан критерий оптимального приема: идеальный наблюдатель (или наблюдатель Котельникова) который минимизирует среднюю вероятность ошибки.
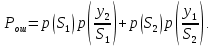
Находим оптимальное правило решение и структурную схему оптимального приемника (оптимального РУ) для указанных выше условий передачи сигналов S1(t) и S2(t):
-
для решения используем общее для приемников двоичных сигналов:
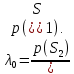
-если λ(х)>λ0 , в пользу сигнала S1, иначе S2.
Для упрощенного решения положим вначале, что p(S1)=p(S2)=0,5;тогда λ0=1. В этом случае критерий идеального наблюдателя совпадает с критерием максимального правдоподобия.
-
для определения функции правдоподобия w(x/S1) и w(x/S2), которые при произвольной длительности сигналов Т будут многомерными. Пусть, что на вход приемника поступает сигнал (см.рис.6):
x(t)=S1(t)+ξ(t), 0≤t≤T.
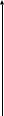
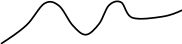х(t)ξ(t) S1(t)
x(ti)
Δt0 t1 t2 ti tk t
Рис.6 – сигнал на входе приемника.
Берется k отсчетов сигнала x(t) через одинаковые интервалы Δt, равные интервалу корреляции помехи τ
n и рассматриваются отсчетные значения суммы сигналов S1(t) и помехи ξ(t) в различных сечениях ti. Отсюда получаем оптимальное правило решения в виде неравенства:
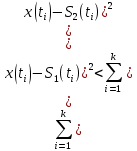
В интегральной форме:
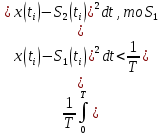
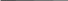Более компактно (черта означает усреднение по времени):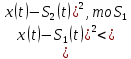
Если вероятности передачи сигналов S1(t) и S2(t) не одинаковы, т.е. р(S1)≠р(S2), то неравенство принимает вид: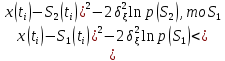
Полученному правилу соответствует структурная схема приемника (см.рис.7) :
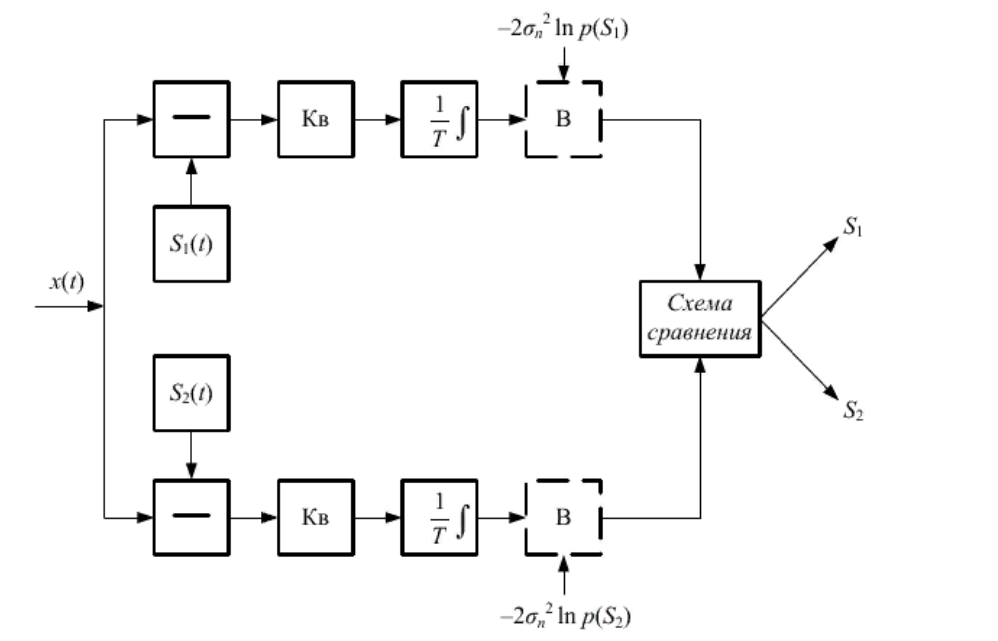
Рис.7- структурная схема оптимального приемника Котельникова.
Схема содержит следующие элементы:
- два генератора опорных сигналов: S1(t) и S2(t), которые генерируют точно такие же сигналы, которые могут поступить на вход приемника;
- два вычитающих устройства;
- два квадратора;
- два интеграла;
- схему сравнения, которая в соответствии с оптимальным правилом решения в компактной форме, выдает сигнал S1 и S2;
Сложность реализации в том, что генераторы S1(t) и S2(t) должны выдавать сигналы, идентичные по форме сигналам, ожидаемым на входе приемника, поэтому эти генераторы должны синхронизироваться приходящими сигналами, а это сделать довольно трудно.
Вероятность ошибки в оптимальном приемнике:
В приемнике Котельникова вероятность ошибки зависит не отношения мощности сигнала к мощности сигнала к мощности помехи, а от отношения энергии сигнала к спектральной плотности помехи. Для оптимального приемника ОФМ:
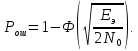
где Ф(z)- интеграл вероятности (табулированная функция).Еэ- эквивалентная энергия разности сигналов (S1(t)-S2(t)).
N0- спектральная плотность мощности помехи.
При этом для различных видов модуляции Еэ определяется через энергию одного из сигналов, а в окончательную формулу вводят величину:
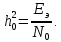
Следовательно, в приемнике Котельникова, который также называется когерентным, вероятность ошибки зависит не от отношения мощности сигнала к мощности помехи, а от отношения энергии сигнала к спектральной плотности помехи. Это позволяет, не меняя мощности сигнала, увеличить его энергию за счет увеличения длительности.
4.2 Сравнительный анализ помехоустойчивости для разных видов модуляции:
Потенциальная помехоустойчивость для приемника с различными видами модуляции:
- для дискретной амплитудной модуляции (ДАМ):
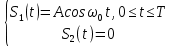
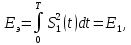(т.е. Еэ равна энергии первого сигнала).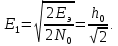
Подставив это выражение в общую формулу для вероятности ошибки, получим:
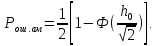
- для дискретная частотная модуляция(ДЧМ):
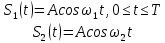
При ЧДМ сигналы являются взаимоортогональными, поэтому их функция взаимной корреляции равна нулю. Благодаря равной амплитуде сигналов S1(t) и S2(t) Е1=Е2, значит:
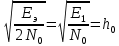
подставляя эту величину получаем:
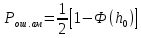
- для дискретной фазовой модуляции(ДФМ):
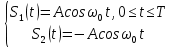
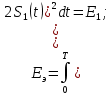
Следовательно,
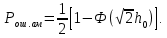
Сравнивая между собой формулу, видно, что для достижения заданной вероятности ошибки при ДЧМ требуется величина U0 в
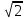раз больше, чем при ДФМ, а при ДАМ в 2 раза больше, чем при ДФМ.Значит, что переход от ДАМ к ДЧМ дает двукратный выигрыш по мощности