Добавлен: 09.11.2023
Просмотров: 249
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, а к ДФМ- четырехкратному выигрышу.
Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции.
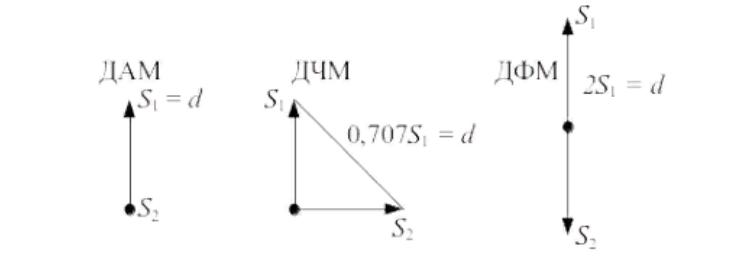
Рис.8- векторные диаграммы сигналов дискретной модуляции.
При одинаковой средней мощности сигналов амплитудная модуляция не имеет проигрыш по сравнению с частотой, а по сравнению с фазовой имеет проигрыш в два раза мощности. Тем не менее при применении ЧМ помехоустойчивость возрастает по сравнению с АМ. Следовательно, реальная помехоустойчивость при ЧМ близка к оптимальной, а при АМ значительно меньше.
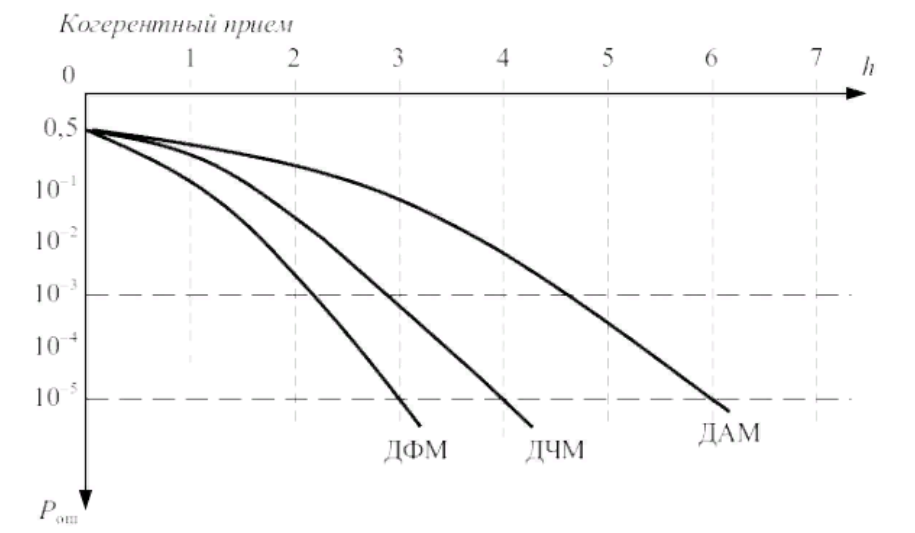
Рис.9– Кривые помехоустойчивости дискретной модуляции.
4.3 Приемник Котельникова применительно ОФм
При ДАМ расстояние между векторами сигналов S1 и S2 равно длине вектора S1, при ДЧМ это расстояние равно S1×
, при ДФМ это расстояние и 2S1(t). Энергия же пропорциональна квадрату разности сигналов.
Для ОФМ оптимального приемника, при Рс=1,1×10-3 Вт и Т=12×10-6 с. Значит, вероятность ошибки равна:
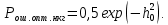
где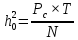
, N=10-9Вт/Гц.
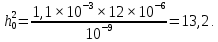
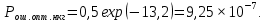
(а неоптимального приемника Рош.опт.нкг.=5,04×10-4)
4.4 Описание сущность оптимальной фильтрации. Оптимальный фильтр
Оптимальная фильтрация дискретных сигналов:
Оптимальный приемник является корреляционным; сигнал на его выходе представляет собой функцию корреляции принимаемого сигнала x(t) и ожидаемого S1(t), благодаря чему обеспечивает максимальное возможное отношение сигнал/шума h02.
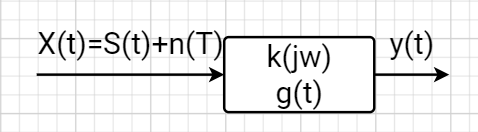
Рис.10 – сущность оптимальной фильтрации.
Критерий оптимальности фильтра- максимальное отношение сигнал/шум.
Отношение сигнал-помеха для оптимального фильтра
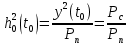
где Рс=у(t0)- мощность сигнала на выходе фильтра в момент t0.
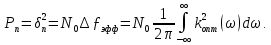
где Рп – мощность (дисперсия) помехи на выходе фильтра
Δƒэфф – эффективная полоса пропускания оптимального фильтра.
Подставляя выражение получим:
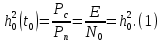
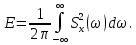
E- энергия сигнала S(t) на выходе фильтра.
Из формулы (1) видно, что отношение сигнала/помеха численно равно отношению сигнала к спектральной плотности помехи (как в приемнике Котельникова) и не зависит от формы сигнала. Так как энергия сигнала равна произведению мощности сигнала на его длительности. То для повышения помехоустойчивости систем связи с использованием согласованных фильтров(СФ) можно увеличивать длительность элементарных сигналов, что и делается в широкополосных системах связи.
Импульсная характеристика оптимального фильтра:
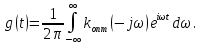
Подставив :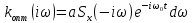
то получим: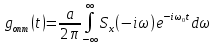
А так как на основании преобразование Фурье:
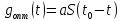
Таким образом, функция g(t) отличатся от S(t) только постоянным множителем а, смещением на величину t0 и знаком аргумента t.
На рис.11 в качества примера приведен некоторый сигнал S(t), зеркально перевернутый сигнал S(-t) и функциями g(t)=aS(t0-t).
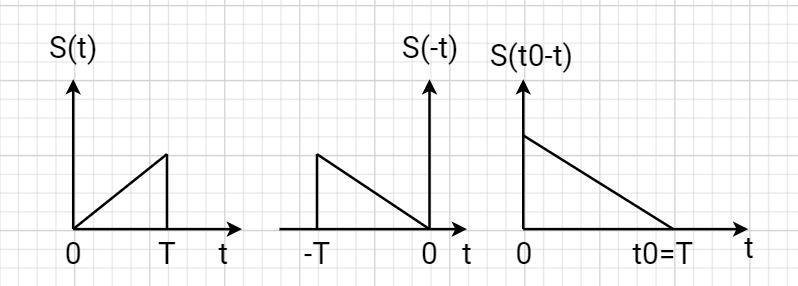
Рис.11- пример получения g(t) СФ.
Величину t0 обычно берут равной длительности сигнал Т. При поступлении на вход системы сигнала x(t) определяется известным интегралом Дюамеля:
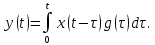
На вход оптимального фильтра поступает аддитивная смесь содержащая сигнал S(t), с которым фильтр согласован, и помех ξ(t), следовательно, получаем:
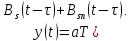
На выходе согласованного фильтра получаем под действием сигнала функции корреляции сигнала, а под действием помехи- функцию взаимной корреляции сигнала и помехи. Если на входе фильтра только помеха (без сигнала), на выходе получаем только функцию взаимной корреляции помехи и сигнала, с которой фильтр согласован.
Фильтр будет оптимальным, если его АЧХ с точностью до постоянного множителя соответствует спектру сигнала.
4.5 Схема оптимального приемника фильтра, согласованного с прямоугольными импульсами
Так как в результате фильтрации не зависит от формы сигнала, следовательно, фильтр может быть применен и без детектора. Тогда оптимальный приемник полностью известных сигналов может быть реализован в виде двух согласованных фильтров и устройства сопротивления.
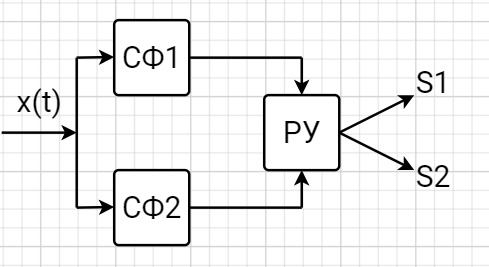
Рис.12- Оптимальный приемник на СФ
Рассмотрим согласованный фильтр для прямоугольного фильтра для прямоугольного импульса длительности T. Спектральная плотность такого импульса равна:
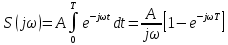
для согласованного фильтра в случае t0=T:
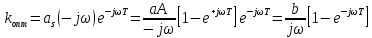
Можно легко построить схему фильтра. Т.к. из теории электрических цепей известно, что деление на jω означает интегрирование сигнала, а множитель e-jωt означает задержку сигнала на время T, в результате схема фильтра будет содержать интегратор, линию задержки и вычитатель.
Рис.13 – пример реализации СФ.
Таким образом, на выходе фильтра получится треугольный импульс с основанием 2T (это – функция корреляции входного импульса прямоугольной формы). Так как выходного сигнала на отрезке времени от T до 2T будет накладываться на входной сигнал следующего импульса, то это является недостатком оптимального фильтра.
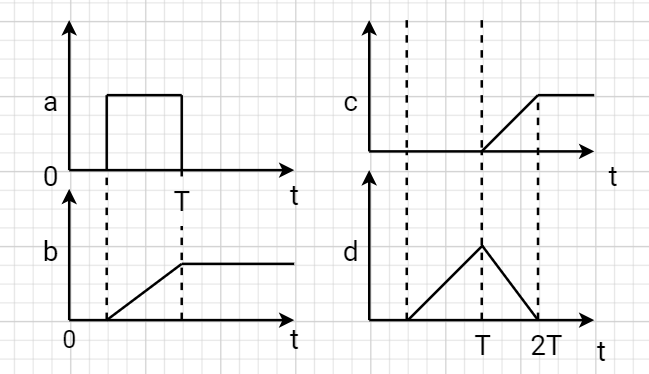
Рис.14- Вид сигналов в различных точках СФ.
Поэтому на практике часто применяют упрощенную схему фильтра, содержащую схему фильтра, содержащую интегрирующую RC-цепь (RC>> T) и ключ K.
В момент T окончания входного импульса ключ K замыкается, конденсатор интегратора быстро разряжается через ключ, и схема готова к приему следующего импульса.
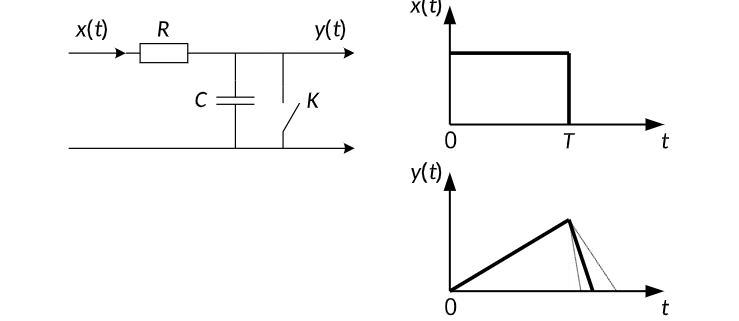
Рис.15 – пример кинематического фильтра для видеоимпульса.
ГЛАВА 5 ПЕРЕДАЧА АНАЛОГОВЫХ СИГНАЛОВ МЕТОДОМ ИКМ.
ИКМ представляет собой один из возможных видов импульсной модуляции, который суммирует в себе все положительные свойства приемов дискретизации, квантования и кодирования.
Сущность ИКМ:
Непрерывное сообщение дискретизируется по времени через интервал ∆t ( по теореме Котельникова), полученные отсчеты мгновенных значений квантуются (дискретизируются по уровню); затем полученная последовательность квантованных значений непрерывного сообщения представляется посредством кодирования в виде последовательности кодовых комбинаций. Чаще всего кодирование сводится к записи номера уровня в двоичной системе счисления. При ИКМ модуляции передача отдельных значений сигнала сводится к передаче определенных групп импульсов. Эти группы передаются друг за другом через относительно большие промежутки времени по сравнению с длительностью отдельных импульсов.
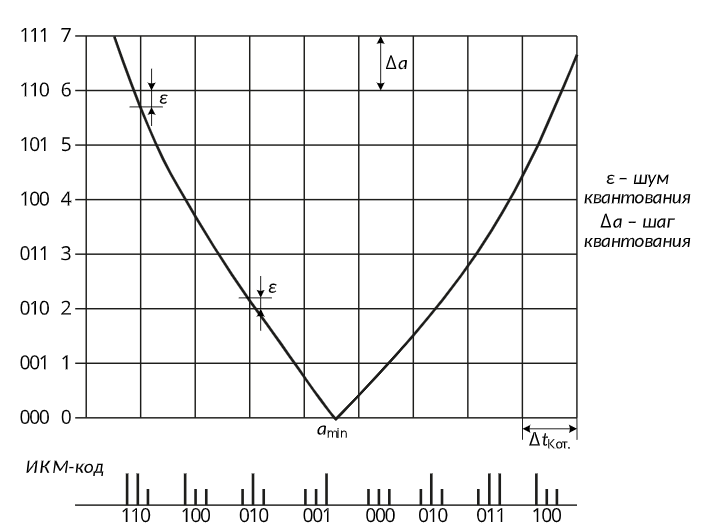
Рис.16 -Сущность получения кодовых комбинаций («цифры») и кода ИКМ
Определим число разрядов применяемого двоичного кода по заданному числу уровней квантования N по формуле: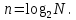 
Где N- число заданных уровней квантования сигнала ИКМ (N=256).
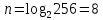
Кодовые комбинации для кодирования квантованных значений мгновенных отсчетов при количестве уровней квантования, равном 256, должны состоять из 8 разрядов. От числа разрядов кода n, а также от пик-фактора аналогового сигнала зависит отношение мощности сигнала к мощности шума квантования:
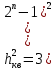
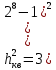
Достоинства ИКМ:
1. Основное техническое преимущество цифровых систем перед непрерывными – высокая помехоустойчивость (не происходит накапливание помехи при переприемах).
2. Широкое использование в аппаратуре преобразования сигналов современной элементарной базы цифровой вычислительной техники и микроэлектроники.
3. Возможность приведения всех видов передаваемой информации к цифровой форме позволит осуществить интеграцию систем передачи и систем коммуникации, а также расширить область использования техники при построении аппаратуры связи и единой автоматизированной сети связи.
4. Аппаратуре не требуются настройки.
Недостатки ИКМ:
Основным недостатком является то, что преобразование непрерывных сообщений в цифровую форму в системах ИКМ сопровождается округлением мгновенных значений до ближайших разрешенных уровней квантования.
Возникающая при этом погрешность преобразования является неустранимой, но контролируемой (т.к. не превышает половины шага квантования). При передаче аналогового сигнала его величина (мгновенная амплитуда) изменяется в пределах от amin до amax.
Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции.
Рис.8- векторные диаграммы сигналов дискретной модуляции.
При одинаковой средней мощности сигналов амплитудная модуляция не имеет проигрыш по сравнению с частотой, а по сравнению с фазовой имеет проигрыш в два раза мощности. Тем не менее при применении ЧМ помехоустойчивость возрастает по сравнению с АМ. Следовательно, реальная помехоустойчивость при ЧМ близка к оптимальной, а при АМ значительно меньше.
Рис.9– Кривые помехоустойчивости дискретной модуляции.
4.3 Приемник Котельникова применительно ОФм
При ДАМ расстояние между векторами сигналов S1 и S2 равно длине вектора S1, при ДЧМ это расстояние равно S1×
, при ДФМ это расстояние и 2S1(t). Энергия же пропорциональна квадрату разности сигналов.Для ОФМ оптимального приемника, при Рс=1,1×10-3 Вт и Т=12×10-6 с. Значит, вероятность ошибки равна:
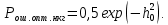
где
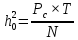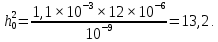
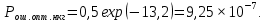
, N=10-9Вт/Гц. (а неоптимального приемника Рош.опт.нкг.=5,04×10-4)
4.4 Описание сущность оптимальной фильтрации. Оптимальный фильтрОптимальная фильтрация дискретных сигналов:
Оптимальный приемник является корреляционным; сигнал на его выходе представляет собой функцию корреляции принимаемого сигнала x(t) и ожидаемого S1(t), благодаря чему обеспечивает максимальное возможное отношение сигнал/шума h02.
Рис.10 – сущность оптимальной фильтрации.
Критерий оптимальности фильтра- максимальное отношение сигнал/шум.
Отношение сигнал-помеха для оптимального фильтра
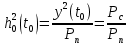
где Рс=у(t0)- мощность сигнала на выходе фильтра в момент t0.
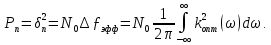
где Рп – мощность (дисперсия) помехи на выходе фильтра
Δƒэфф – эффективная полоса пропускания оптимального фильтра.
Подставляя выражение получим:
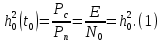
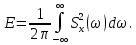
E- энергия сигнала S(t) на выходе фильтра.
Из формулы (1) видно, что отношение сигнала/помеха численно равно отношению сигнала к спектральной плотности помехи (как в приемнике Котельникова) и не зависит от формы сигнала. Так как энергия сигнала равна произведению мощности сигнала на его длительности. То для повышения помехоустойчивости систем связи с использованием согласованных фильтров(СФ) можно увеличивать длительность элементарных сигналов, что и делается в широкополосных системах связи.Импульсная характеристика оптимального фильтра:
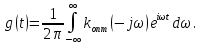
Подставив :
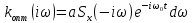
то получим:
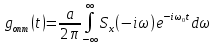
А так как на основании преобразование Фурье:
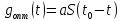
Таким образом, функция g(t) отличатся от S(t) только постоянным множителем а, смещением на величину t0 и знаком аргумента t.
На рис.11 в качества примера приведен некоторый сигнал S(t), зеркально перевернутый сигнал S(-t) и функциями g(t)=aS(t0-t).
Рис.11- пример получения g(t) СФ.
Величину t0 обычно берут равной длительности сигнал Т. При поступлении на вход системы сигнала x(t) определяется известным интегралом Дюамеля:
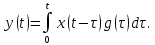
На вход оптимального фильтра поступает аддитивная смесь содержащая сигнал S(t), с которым фильтр согласован, и помех ξ(t), следовательно, получаем: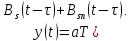 На выходе согласованного фильтра получаем под действием сигнала функции корреляции сигнала, а под действием помехи- функцию взаимной корреляции сигнала и помехи. Если на входе фильтра только помеха (без сигнала), на выходе получаем только функцию взаимной корреляции помехи и сигнала, с которой фильтр согласован.
Фильтр будет оптимальным, если его АЧХ с точностью до постоянного множителя соответствует спектру сигнала.
4.5 Схема оптимального приемника фильтра, согласованного с прямоугольными импульсами
Так как в результате фильтрации не зависит от формы сигнала, следовательно, фильтр может быть применен и без детектора. Тогда оптимальный приемник полностью известных сигналов может быть реализован в виде двух согласованных фильтров и устройства сопротивления.
Рис.12- Оптимальный приемник на СФ
Рассмотрим согласованный фильтр для прямоугольного фильтра для прямоугольного импульса длительности T. Спектральная плотность такого импульса равна:
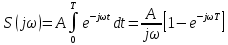
для согласованного фильтра в случае t0=T:
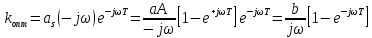
Можно легко построить схему фильтра. Т.к. из теории электрических цепей известно, что деление на jω означает интегрирование сигнала, а множитель e-jωt означает задержку сигнала на время T, в результате схема фильтра будет содержать интегратор, линию задержки и вычитатель.
Рис.13 – пример реализации СФ.
Таким образом, на выходе фильтра получится треугольный импульс с основанием 2T (это – функция корреляции входного импульса прямоугольной формы). Так как выходного сигнала на отрезке времени от T до 2T будет накладываться на входной сигнал следующего импульса, то это является недостатком оптимального фильтра.
Рис.14- Вид сигналов в различных точках СФ.
Поэтому на практике часто применяют упрощенную схему фильтра, содержащую схему фильтра, содержащую интегрирующую RC-цепь (RC>> T) и ключ K.В момент T окончания входного импульса ключ K замыкается, конденсатор интегратора быстро разряжается через ключ, и схема готова к приему следующего импульса.
Рис.15 – пример кинематического фильтра для видеоимпульса.
ГЛАВА 5 ПЕРЕДАЧА АНАЛОГОВЫХ СИГНАЛОВ МЕТОДОМ ИКМ.
ИКМ представляет собой один из возможных видов импульсной модуляции, который суммирует в себе все положительные свойства приемов дискретизации, квантования и кодирования.
Сущность ИКМ:
Непрерывное сообщение дискретизируется по времени через интервал ∆t ( по теореме Котельникова), полученные отсчеты мгновенных значений квантуются (дискретизируются по уровню); затем полученная последовательность квантованных значений непрерывного сообщения представляется посредством кодирования в виде последовательности кодовых комбинаций. Чаще всего кодирование сводится к записи номера уровня в двоичной системе счисления. При ИКМ модуляции передача отдельных значений сигнала сводится к передаче определенных групп импульсов. Эти группы передаются друг за другом через относительно большие промежутки времени по сравнению с длительностью отдельных импульсов.
Рис.16 -Сущность получения кодовых комбинаций («цифры») и кода ИКМ
Определим число разрядов применяемого двоичного кода по заданному числу уровней квантования N по формуле: 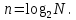Где N- число заданных уровней квантования сигнала ИКМ (N=256).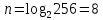 Кодовые комбинации для кодирования квантованных значений мгновенных отсчетов при количестве уровней квантования, равном 256, должны состоять из 8 разрядов. От числа разрядов кода n, а также от пик-фактора аналогового сигнала зависит отношение мощности сигнала к мощности шума квантования:
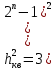
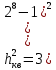
Достоинства ИКМ:
1. Основное техническое преимущество цифровых систем перед непрерывными – высокая помехоустойчивость (не происходит накапливание помехи при переприемах).
2. Широкое использование в аппаратуре преобразования сигналов современной элементарной базы цифровой вычислительной техники и микроэлектроники.
3. Возможность приведения всех видов передаваемой информации к цифровой форме позволит осуществить интеграцию систем передачи и систем коммуникации, а также расширить область использования техники при построении аппаратуры связи и единой автоматизированной сети связи.
4. Аппаратуре не требуются настройки.
Недостатки ИКМ:
Основным недостатком является то, что преобразование непрерывных сообщений в цифровую форму в системах ИКМ сопровождается округлением мгновенных значений до ближайших разрешенных уровней квантования.
Возникающая при этом погрешность преобразования является неустранимой, но контролируемой (т.к. не превышает половины шага квантования). При передаче аналогового сигнала его величина (мгновенная амплитуда) изменяется в пределах от amin до amax.