Добавлен: 09.11.2023
Просмотров: 251
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 ГЛАВА 6 ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ.
ГЛАВА 6 ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ.
При передаче дискретных сигналов для уменьшения вероятности ошибок можно применить помехоустойчивое кодирование.
Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передаче информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется. Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки. Принципиальная возможность обнаружения и исправления ошибок появляется, если для передачи знаков сообщения использовать лишь часть из возможных последовательностей, называемых в этом случае разрешенными. При декодировании принятая кодовая последовательность тестируется на предмет разрежённости. Принятие неразрешенной последовательности является признаком ошибки.
Существует множество помехоустойчивых кодов. Их можно классифицировать по различным признакам. Одним из них является основание кода m или число используемых символов. Наиболее простыми являются бинарные коды (m=2).
Все известные в настоящее время коды могут быть разделены на две большие группы: блочные и непрерывные.
Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно.
 Непрерывные-это первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.
Непрерывные-это первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.
Двоичные блочные коды называются линейными, если сумма по модулю двух любых разрешенных кодовых комбинаций также принадлежит данному коду. Существует подкласс линейных двоичных кодов, названных циклическими. В них каждая новая комбинация, получаемая путем перестановки кодовых символов разрешенных кодовых комбинаций, также является разрешенной.
Корректирующую способность кода определяет расстояние между двумя кодовыми комбинациями. Кодовое расстояние(dij)- это суммарный результат сложения по модулю m их одноименных кодовых символов. Для двоичных кодов это число разрядов, в которых символы кодовых комбинаций не совпадают. Кодовое расстояние кода, содержащее более двух кодов комбинации, есть минимальное расстояние из совокупности расстояний между различными парами кодовых комбинаций кода. Код является корректирующим только при условии d>1. Чем больше кодовое расстояние, тем лучше корректирующая способность кода. Кратность гарантированно обнаруживаемых и исправляемых кодом ошибок определяется отношениями:
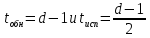
 На практике применяется как блочное, так и непрерывное кодирование. При блочном кодировании последовательный цифровой код символов разбивается на блоки по k символов в каждом. Затем каждому такому k-значному блоку сопоставляется n-значный блок, в котором k кодовых символов называется информационными, а æ=(n-k)- корректирующими. Самый простой метод помехоустойчивого кодирования- контроль чётности Контроль чётности-это добавление одного бита четности после информационных символов, если количество «1» нечетное- добавляем 0, если четное- добавляем 1. Контроль чётности имеет следующие параметры:
На практике применяется как блочное, так и непрерывное кодирование. При блочном кодировании последовательный цифровой код символов разбивается на блоки по k символов в каждом. Затем каждому такому k-значному блоку сопоставляется n-значный блок, в котором k кодовых символов называется информационными, а æ=(n-k)- корректирующими. Самый простой метод помехоустойчивого кодирования- контроль чётности Контроль чётности-это добавление одного бита четности после информационных символов, если количество «1» нечетное- добавляем 0, если четное- добавляем 1. Контроль чётности имеет следующие параметры: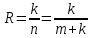
где n – количество символов закодированного сообщения (результата
кодирования);
m – количество проверочных символов, добавляемых при кодировании;
k – количество информационных символов.
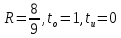
Избыточность кода определяется по формуле:
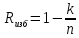
где,
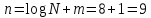
m=1, так как используется метод избыточности равной единице.
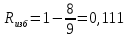
Вероятность ошибки, необнаруженной этим кодом при независимых ошибках, определяется биноминальным законом:
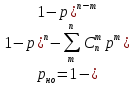
 где, р=рош=0,000504- вероятность ошибки;
где, р=рош=0,000504- вероятность ошибки;рпп=[1-р]п- вероятность правильного приема;
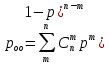 - вероятность приема с обнаруженными ошибками.
- вероятность приема с обнаруженными ошибками.Рно=7,09097×10-6
Любой код способен обнаруживать и исправлять ошибки, если не все кодовые комбинации используются для передачи сообщений.
Сформулируем принципы обнаружения и исправления ошибок при декодировании. В декодере хранится «список» всех разрешенных кодовых комбинаций. При декодировании с обнаружением ошибок принятая кодовая комбинация сравнивается с каждой из разрешенных и, если она не совпадает ни с одной разрешенной, то считается ошибочной, т.к. находится в области запрещенных – ошибка обнаруживается. Ошибка не обнаруживается, когда переданная разрешенная кодовая комбинация на приеме переходит в другую разрешенную. Декодирование с исправлением ошибок основано на двух операциях: определении расстояний между принятой комбинацией и каждой из разрешенной и затем отыскания разрешенной комбинации, имеющей минимальной расстояние от поступившей комбинации. При этом принятая кодовая комбинация отождествляется с той комбинацией, до которой расстояние минимально.
 ГЛАВА 7 СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
ГЛАВА 7 СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
Цели помехоустойчивого и статистического кодирования различны. При помехоустойчивом кодировании увеличивается избыточность за счет введения дополнительных элементов в кодовые комбинации. При статистическом кодировании, наоборот, уменьшается избыточность, благодаря чему повышается производительность источника сообщений.
В математической теории связи (теории информации) исходят из того, что в некотором сообщении xi количество информации I(xi) зависит не от ее конкретного содержания, степени важности и т.д., а того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений.
При определении количества информации исходят из следующих требований:
1. Количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении.
2. Количество информации о достоверном событии (P(xi)=1) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении.
Количественной мерой информации является логарифмическая функция вероятности сообщения:

Основание логарифма чаще всего берется 2. При этом единица информации называется двоичной единицей или бит. Она равна количеству информации в сообщении, происходящем с вероятностью 0,5, т.е. таком, которое может с равной вероятностью произойти или не произойти.
 В теории информации чаще всего необходимо знать не количество информации
В теории информации чаще всего необходимо знать не количество информации Если имеется ансамбль (полная группа) из k сообщений с x1, x2, … xi, xk с вероятностями p(xi
) … p(xk), то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений Н(х) определяется формулой:
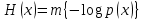
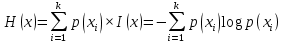
Размерность энтропии - количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределённости выбора того или другого сообщения.
Свойства энтропии:
-
Чем больше неопределенность выбора сообщений, тем больше энтропия. Неопределённость максимальна при равенстве вероятностей выбора каждого сообщения: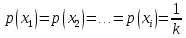
В это случае
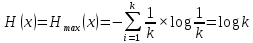
Вычислим энтропию данного источника:
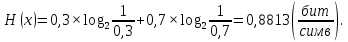
Чем ближе энтропия источника к максимальной, тем рациональнее работает источник. Чтобы судить о том, насколько хорошо используется источник свой алфавит, вводят понятие избыточности источника сообщения.

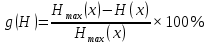
Производительность источника определяется количеством информации, передаваемой в единицу времени. Измеряется производительность количеством двоичных единиц информации (бит) в секунду. Если все сообщения имеют одинаковую длительность τ, то производительность
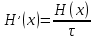
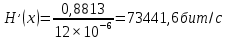
 Если же различные элементы сообщения имеют разную длительность, то в приведённой формуле надо учитывать среднюю длительность τ, равную математическому ожиданию величины τ:
Если же различные элементы сообщения имеют разную длительность, то в приведённой формуле надо учитывать среднюю длительность τ, равную математическому ожиданию величины τ: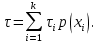
а производительность источника будет равна:
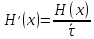
Максимально возможная производительность дискретного источника равна:
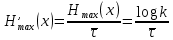
Для двоичного источника, имеющего одинаковую производительность элементов сообщения (k=2,