Добавлен: 09.11.2023
Просмотров: 254
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
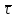 =τ) имеем
=τ) имеем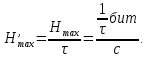
Сопоставив формулу, получим:
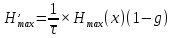
Увеличить производительность можно путем уменьшения длительности элементов сообщения, однако возможность эта ограничивается полосой пропускания канала связи. Поэтому производительность источника можно увеличить за счет более экономного использования полосы пропускания, например, путем применения сложных многоуровневых сигналов:

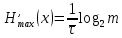 ,
,где m- основание кода.
Основой статистического (оптимального) кодирования сообщений является теорема К. Шеннона для каналов связи без помех. Кодирование по методу Шеннона-Фано-Хаффмана называется оптимальным. так как при этом повышается производительность дискретного источника, и статистическим, так как для реализации оптимального кодирования необходимо учитывать вероятности появления на выходе источника каждого элемента сообщения (учитывать статистику сообщений). Идея такого кодирования заключается в том, что, применяя неравномерный неприводимый код, наиболее часто встречающиеся сообщения (буквы или слова) кодируются короткими комбинациями этого кода, а редко встречающиеся сообщения кодируются более длительными комбинациями.
Перед осуществлением статистического кодирования образуем трехбуквенную комбинацию, состоящую из элементов двоичного кода 1 и 0. Число возможных кодовых слов определяется выражением m=kn , где k- алфавит букв первичного сообщения, n- длина кодового слова.
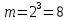
Вероятность передачи 1 в соответствии с вариантом р(1)=0,3 , р(0)=0,7. Вычислим вероятности этих трехбуквенных комбинаций (по теореме умножения вероятностей):
| Кодовая комбинация xi | обозначение | Р(xi) |
| 000 | x1 | 0,343 |
| 001 | x2 | 0,147 |
| 010 | x3 | 0,147 |
| 011 | x4 | 0,063 |
| 100 | x5 | 0,147 |
| 101 | x6 | 0,063 |
| 110 | x7 | 0,063 |
| 111 | x8 | 0,027 |
| | | 1 |
| x1 | 0,343 | 0 | | |||||||||||||||||||
| x2 | 0,147 | 0 0 1 | 1 | | ||||||||||||||||||
| x3 | 0,147 | 1 | 0,21 | 0,546 | | |||||||||||||||||
| x4 | 0,063 | 0 1 | | | | | ||||||||||||||||
| x5 | 0,147 | 0 0 1 | 0,336 | | | | ||||||||||||||||
| x6 | 0,063 | 1 | 0,126 | 0,189 | ||||||||||||||||||
| x7 | 0,063 | 0 1 | | | | | | | | |||||||||||||
| x8 | 0,027 | 1 | 0,09 | | | | | | | | ||||||||||||

| x1 | 0 | 1 | 0,343 |
| x2 | 100 | 3 | 0,441 |
| x3 | 101 | 3 | 0,441 |
| x4 | 110 | 3 | 0,189 |
| x5 | 11100 | 5 | 0,735 |
| x6 | 11101 | 5 | 0,315 |
| x7 | 11110 | 5 | 0,315 |
| x8 | 11111 | 5 | 0,135 |
| | | | |
Рассчитаем производительность источника при статистическом кодировании:
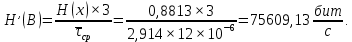
 ГЛАВА 8 ПРОПУСКНАЯ СПОСОБНОСТЬ ДВОИЧНОГО КАНАЛА СВЯЗИ
ГЛАВА 8 ПРОПУСКНАЯ СПОСОБНОСТЬ ДВОИЧНОГО КАНАЛА СВЯЗИ
Пропускная способность двоичного симметричного канала связи определяется по формуле:
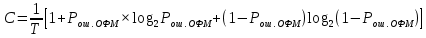
где V=1/T- скорость передачи сообщений (Бод)
Пропускная способность С двоичного канала связи с помехами всегда меньше V, так как при наличии искажений резко снижается ценность принимаемой информации.
В результате С=82812,5 бит/сек.
Т.к. пропускная способность канала связи оказалась больше производительности источника как с применением оптимального кодирования, так и без него, то можно сделать вывод: по данному каналу связи возможна передача информации без потерь, канал загружен не полностью.
 ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
Современная теория связи позволяет достаточно полно оценить различные системы связи по их помехоустойчивости и эффективности и тем самым определить какие из этих систем являются наиболее перспективными.
В курсовой работе мы разобрали структурную схемы системы связи для передачи, как двоичных данных, так и аналоговых сигналов используя, аналого-цифровой преобразователь. Передача осуществляется некогерентной относительной фазовой модуляцией. В работе показано, что данный вид модуляции обладает наибольшей помехоустойчивостью. При аддитивной помехи типа "гауссовского белого шума" вероятность ошибки в приеме сигнала составляет 0,000504. При введении статистического кодера достигается увеличение производительности источника, за счет введения неравномерных кодов. Одним из алгоритмов статистического кодирования является алгоритм Хаффмана. Пропускная способность канала связи позволяет передачу данных, как со статистическим кодером, так и без него. Показано что приемник Котельникова обладает потенциальной помехоустойчивостью. Также потенциальную помехоустойчивость можно достигнуть, используя когерентный прием с оптимальным фильтром.
Теория достаточно четко указывает не только возможности совершенствования существующих систем связи, но и пути создания новых более современных систем.
 СПИСОК ЛИТЕРАТУРЫ
СПИСОК ЛИТЕРАТУРЫ
-
Теория электрической связи: Учебник для вузов / А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Ю. Н. Прохоров.—М.: Радио и связь (в печати). -
Теория передачи сигналов: Учебник для вузов / А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Л.М. Финк.—2-е изд., перераб. и доп.—М.: Радио и связь, 1986.—304 с. -
Теория электрической связи: Учебное пособие.- Новосибирск, СибГУТИ, 2011.-284с. -
Макаров А.А., Чиненков Л.А. Основы теории помехоустойчивости дискретных сигналов: Учеб. пособие.— Новосибирск, СибГУТИ, 1997.—42 с. -
Макаров А.А. Методы повышения помехоустойчивости систем связи.—Новосибирск, СИИС, 1991.—58 с.