Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc

В данной работе используется круговой полутеневой поляриметр (модель СМ - 3).

Устройство и принцип работы прибора.

Поляриметр с наклонной осью, визуальный, настольного типа, закрытой конструкции состоит из головки анализатора с поляризатором, корпуса в сборе, основания в сборе и кюветы.

Оптическая принципиальная схема включает в себя (рис. 1) : лампу 4,


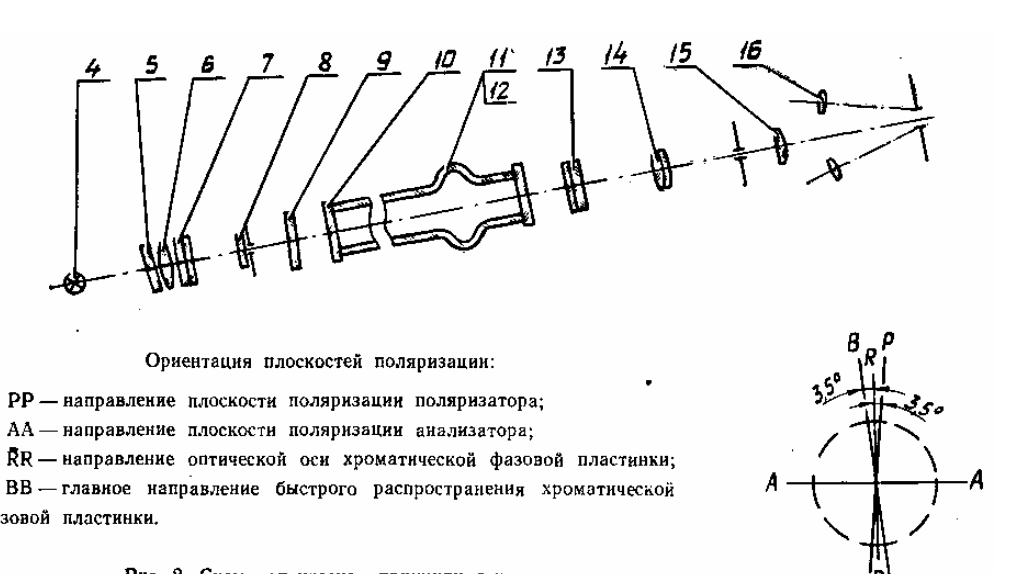
Рис.2. Схема оптическая принципиальная поляриметра СМ - 3.
светофильтр 5, конденсор 6, поляризатор 7, хроматическую фазовую пластинку 8, защитное стекло 9, два покровных стекла 10, трубки 11 и 12, анализатор 13, объектив 14, окуляр 15 и две лупы 16.
В поляриметре применен принцип уравнивания яркостей разделенного на части поля зрения. Яркости полей сравнения уравнивают вблизи полного затемнения поля зрения.

Свет от лампы, пройдя через конденсор и поляризатор, одной частью пучка проходит через хроматическую фазовую пластинку, защитное стекло, кювету и анализатор, а другой частью пучка только через защитное стекло, кювету и анализатор.

Вид поля зрения поляриметра представлен на рис. 3.


Рис. 3. Поле зрения поляриметра.
Уравнивание яркостей полей сравнения производят путем вращения анализатора.

Если между анализатором и поляризатором ввести кювету с оптически активным раствором, то равенство яркостей полей сравнения нарушается. Оно может быть восстановлено поворотом анализатора на угол, равный углу поворота плоскости поляризации раствором.

Следовательно, разностью двух отсчетов, соответствующих равенству яркостей полей сравнения с оптически активным раствором и без него, определяется угол вращения плоскости поляризации данным раствором.

При измерении на поляриметре угла вращения плоскости поляризации правовращающими оптически активными растворами отсчеты по шкале первого отсчетного устройства и лимбу будут от 0 до 35⁰.

При измерении угла вращения плоскости поляризации левовращающими оптически активными растворами отсчеты по шкале первого отсчетного устройства и лимбу будут от 360 до 325⁰ , величина угла вращения определяется: отсчет по шкале первого отсчетного устройства и лимбу минус 360⁰.
Порядок выполнения работы.
Задание 1. Определение удельного вращения водных растворов сахара.

---

1. Включить поляриметр в сеть переменного тока 220 В. Измерения рекомендуется начинать через 10 минут после включения лампы.

2. Открыть крышку кюветного отделения поляриметра, вынуть трубку (кювету). Наполнить ее дистиллированной водой для определения нулевого отсчета. Для этого отвинтить крышку на одном конце трубки (помечено красной краской), снять покровное стеклышко и, держа ее вертикально, наполнить водой до образования выпуклого мениска. Притереть покровное стекло к трубке, сдвигая осторожно эту выпуклость в сторону и стараясь, чтобы в трубке не оказалось воздушных пузырьков. Завинтить крышку. Протереть тряпочкой наружные поверхности покровных стекол, удаляя следы жидкости. Если в трубке окажутся пузырьки воздуха то, наклоняя трубку, их необходимо вывести в выпуклую часть ее. Поместить кювету в камеру.

3. Вращением втулки наблюдательной трубки установить окуляр так, чтобы видеть резкое изображение линии раздела полей сравнения. После этого, вращением ручки поворачивают анализатор и добиваются равенства яркостей полей сравнения в чувствительном положении. При этом в поле зрения не должно наблюдаться окрашивания частей поля зрения и не должно быть заметно резкого выделения стороны хроматической фазовой пластинки.

4. Установку на равномерную яркость полей сравнения повторяют 3 раза со снятием отсчетов по шкале лимба и отсчетного устройства (нониуса) и вычислением среднего арифметического значения. Полученное значение является нулевым отсчетом (₀).

5. Вылить воду из трубки, заполнить ее раствором сахара известной концентрации и вновь поместить в кюветное отделение. Раствор должен быть прозрачным, не иметь взвешенных частиц. Проверить фокусировку окуляра.

6. Нарушенное введением оптически активного вещества равенство освещенности поля зрения восстановить поворотом анализатора. Произвести отсчет нового положения анализатора '. Определяют на сколько градусов повернута шкала лимба по отношению к шкале первого отсчетного устройства, затем по штрихам первого и второго отсчетных устройств, совпадающими со штрихами шкалы лимба, отсчитывают доли градуса. Цена деления шкалы отсчетного устройства 0,02⁰. Оцифровка отсчетного устройства "10" соответствует 0,10⁰.

К числу градусов, взятых по шкале лимба первого отсчетного устройства, прибавляют средний арифметический отсчет по шкале первого и второго отсчетного устройства. Эту операцию повторяют 3 раза и берут среднее арифметическое значение

---

('). Из полученного вычитают нулевой отсчет. Таким образом находят угол поворота плоскости колебаний

 = ' - ₀.

8. Из формулы (5) найти удельное вращение сахара для растворов известной концентрации и найти  _ср..

 =  / L^. С (5)
При расчете длину кюветы выражать в метрах, а концентрацию в кг/м³.
Задание 2. Определение содержания сахара в растворах неизвестной концентрации.

1. 
   Произвести измерения угла  для растворов неизвестной концентрации не менее 3 раз аналогично заданию 1 и рассчитать содержание сахара по формуле
   

С =  / L^.  (6)

2. 
   Данные занести в таблицу.
   
3. 
   Для растворов известной концентрации построить график зависимости угла поворота плоскости поляризации  от концентрации раствора С , откладывая по оси абсцисс - С, а по оси ординат - . Имея измеренные значения  для растворов неизвестной концентрации, по графику найти соответствующие им концентрации. Сравнить полученные значения с рассчитанными в пункте 1.
   

Контрольные вопросы.

1. 
   Дайте определение естественного и поляризованного света.
   
2. 
   Способы получения плоскополяризованного света.
   
3. 
   Назначение поляризатора и анализатора.
   
4. 
   Закон Малюса.
   
5. 
   Оптически активные среды и вращение плоскости поляризации.
   
6. 
   Определение удельного вращения.
   

Литература.

1. 
   Т.И. Трофимова "Курс физики", 1997.
   
2. 
   Физический практикум. П/р Кембровского Г.С., 1986.
   

ЛАБОРАТОРНАЯ РАБОТА № 15.
ИЗУЧЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ НАГРЕТЫХ ТЕЛ И Определение постоянной Стефана- Больцмана.
Вопросы теории.

тела, нагретые до достаточно высоких температур, светятся. Свечение тел, обусловленное нагреванием, называется тепловым (температурным) излучением. Тепловое излучение самое распространенное в природе. Оно совершается за счет энергии теплового движения атомов и молекул вещества (т.е. за счет внутренней энергии) и свойственно всем телам при температуре выше 0⁰ К. Тепловое излучение характеризуется сплошным спектром, положение максимума которого зависит от температуры. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких - преимущественно длинные (инфракрасные).

Основной количественной характеристикой теплового излучения является спектральная плотность энергетической светимости тела Е

---

_,Т.

Е_,Т = (1)

где dW - энергия теплового излучения с единицы площади поверхности тела за единицу времени в интервале длин волн от  до + d. Спектральная плотность энергетической светимости зависит от длины волны , абсолютной температуры тела Т, а также его материала, формы и состояния. Единица спектральной плотности энергетической светимости Дж/м².

Введем монохроматический коэффициент поглощения тела А_{, m} , который равен отношению потока излучения, поглощенного данным телом к потоку излучения, упавшему на это тело,

А_{, Т=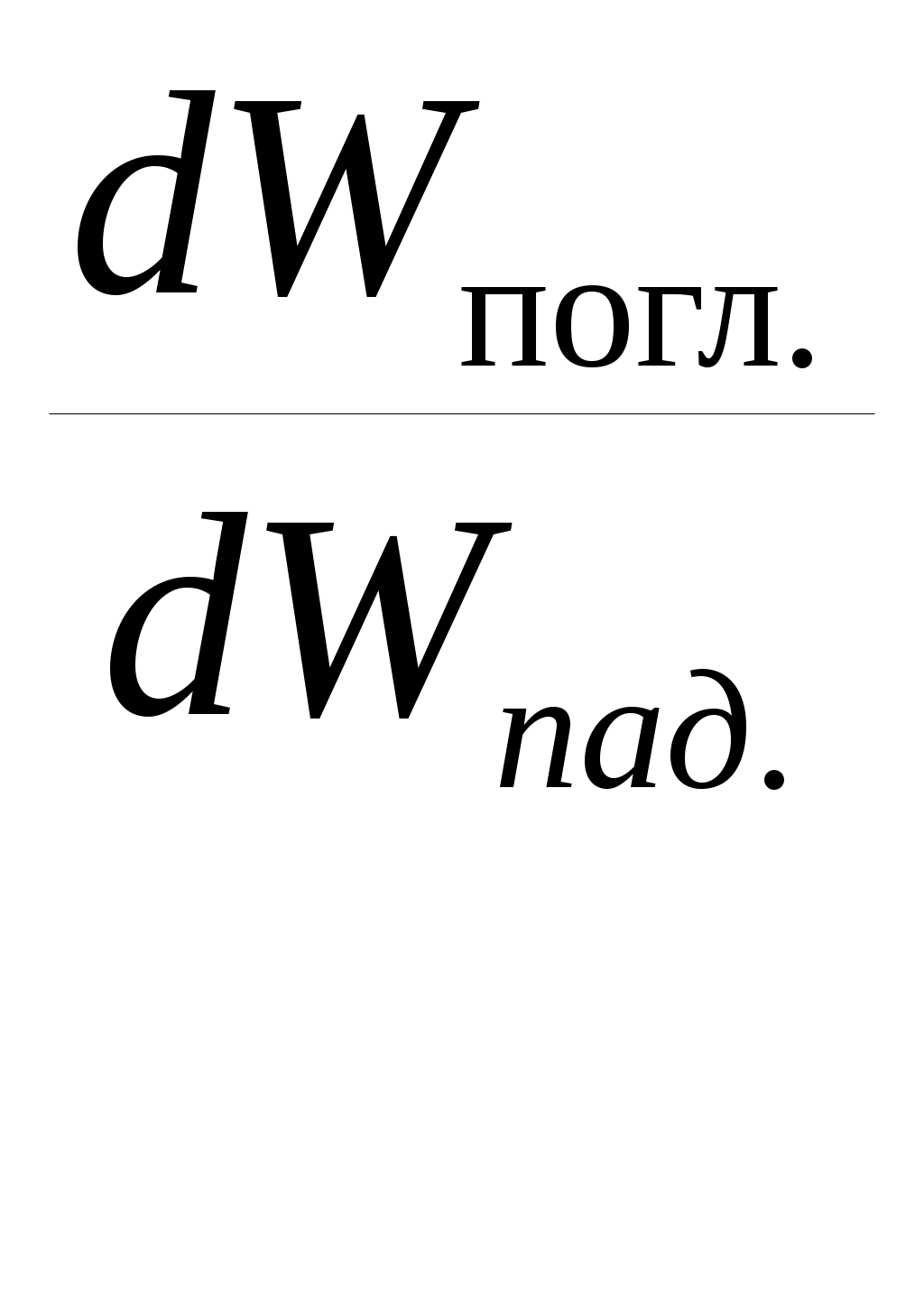} (2)

где А_{, Т} - величина безразмерная. Она зависит, помимо длины волны излучения и температуры тела, от его материала, формы и состояния поверхности.

Тело, способное поглощать полностью при любой температуре все падающее на него световые волны любых частот, направлений распространения и состояний поляризации, называется абсолютно черным. Следовательно при этом А_{, Т} 1.

Абсолютно черных тел в природе нет, однако такие тела, как сажа, платиновая чернь, черный бархат и некоторые другие по оптическим свойствам близки к абсолютно черным телам и их коэффициент поглощения близок к единице. Наиболее совершенной моделью абсолютно черной поверхности может служить небольшое отверстие в непрозрачной стенке замкнутой полости.

Тело, поглощательная способность которого меньше единицы, но одинакова для всех длин волн и зависит только от температуры, материала и состояния поверхности (т.е. А_{, Т = соnst.}  1), называется серым телом.

Между спектральной плотностью энергетической светимости и коэффициентом поглощения любого непрозрачного тела существует соотношение (закон Кирхгофа в дифференциальной форме):

= _,Т (3)

Для произвольной частоты и температуры отношение спектральной плотности энергетической светимости тела к его коэффициенту поглощения одинаково для всех тел и равно спектральной плотности энергетической светимости _,Т абсолютно черного тела, являющейся функцией только длины волны и температуры.

---

Из закона Кирхгофа следует, что если тело при данной температуре Т не поглощает излучения в интервале длин волн от  до + d (А_{, Т}=0), то оно не может при температуре Т равновесно излучать в этом интервале длин волн, так как Е_,Т = А_{, Т} _,Т=0.

Е_Т= Е_,Тd(4)

Представляет собой энергию излучения всех возможных длин волн, испускаемую с единицы поверхности тела за единицу времени.

Энергетическая светимость _ абсолютно черного тела равна:

_Т = _,Тd(5)

Соотношение между энергетической светимостью серого тела и его коэффициентом поглощения имеет вид:

₌ А_Т _Т (6)

Выражение для спектральной плотности энергетической светимости абсолютно черного тела дается знаменитой формулой Планка, исторически первой формулой квантовой теории:

Е_,Т = 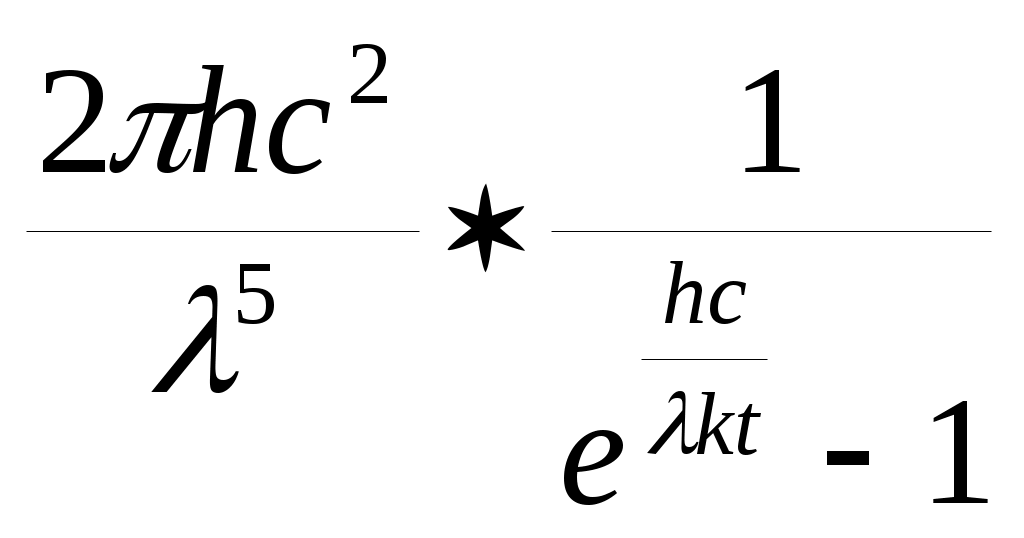(7)

где h -постоянная Планка, с - скорость света , k - постоянная Больцмана, - длина волны.

Согласно гипотезе Планка энергия любой системы изменяется не непрерывно, а определёнными порциями – квантами. Спектральная плотность энергетической светимости, определяемая формулой Планка, прекрасно согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур.

На рис. 1 изображена серия кривых _,Т для различных температур излучающего абсолютно черного тела (спектры излучения).


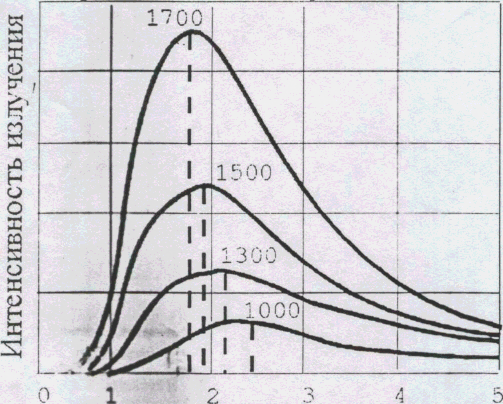
Рис.1. График зависимости интенсивности излучения от длины волны.
Согласно формуле Планка, для каждой длины волны  с ростом температуры показатель

---