Вывод: Сравнивая результаты, полученные при расчете аналитическим способом и при определении усилий по линиям влияния, видно, что результаты совпадают с допустимой относительной погрешностью 3%.




Задача 2. Расчет статически неопределимой рамы методом сил

Заданная система. Жесткость у стержней рамы разная. Примем I1 =I, тогда I2=2I.



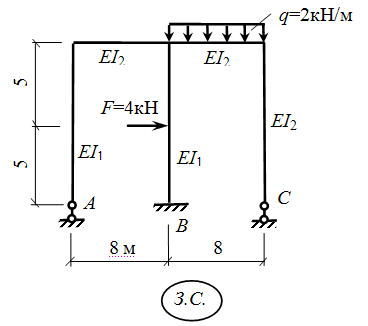
1.Определим степень статической неопределимости заданной системы по формуле:

n=ΣR-Ш-3=5-0-3=2.

Система 2 раза статически неопределима, и для её решения потребуется  два дополнительных уравнения.

Это канонические уравнения метода сил:



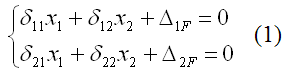
2.Освободим заданную систему от «лишних» связей и получим основную систему. За «лишние» связи в данной задаче примем опору А и опору 

---

С.



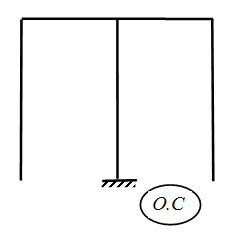
Теперь основную систему следует преобразовать в систему, эквивалентную (равнозначную) заданной.

Для этого загрузим основную систему заданной нагрузкой, действия «лишних» связей заменим их неизвестными реакциями Х1 и Х2  и вместе с системой канонических уравнений (1) данная система будет эквивалентна заданной.



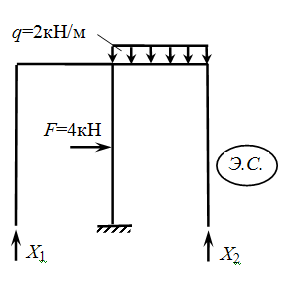
3.По направлению предполагаемой реакции отброшенных опор к основной системе поочередно прикладываем единичные силы Х1=1 и Х2=1 и строим эпюры  .



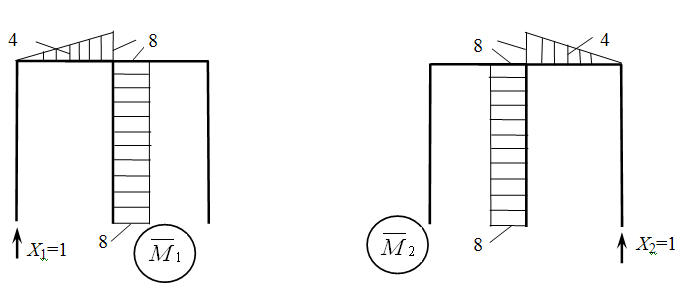
Теперь основную систему загрузим заданной нагрузкой и построим грузовую эпюру МF.



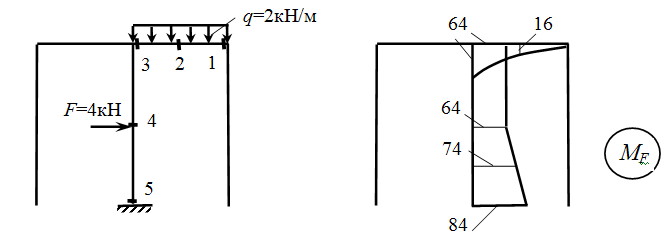
М1=0

М2= -q·4·2 = -16кНм (сжатые волокна внизу)

М3= -q·8·4 = -64кНм (сжатые волокна внизу)

---

М4= -q·8·4 = -64кНм (сжатые волокна справа)

М5= -q·8·4-F·5 = -84кНм (сжатые волокна справа).

4.Определяем коэффициенты и свободные члены канонического уравнения по формуле Симпсона перемножением эпюр (обращаем внимание на разные жесткости участков).



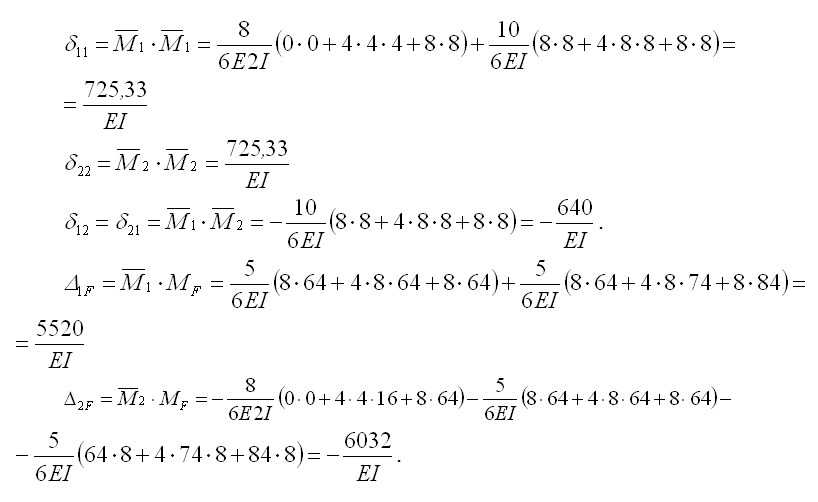
Подставляем в каноническое уравнение, сокращаем на ЕI.



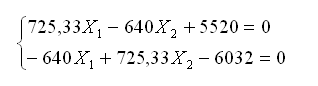
Поделим первое и второе уравнения на сомножители при Х1, а затем из одного уравнения вычтем второе. Найдем неизвестные.

Х2=7,12кН, тогда Х1=-1,14 кН.

5. 
   Строим окончательную эпюру моментов по формуле:
   

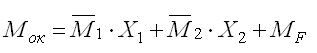
Сначала строим эпюры   :



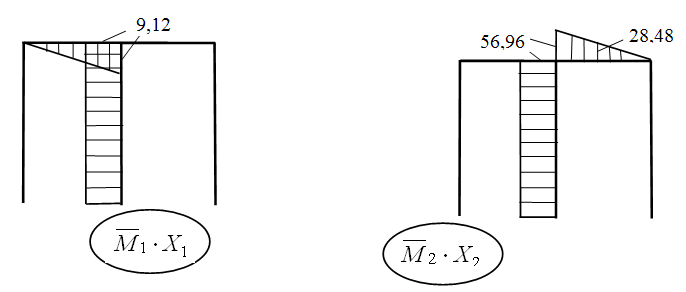
Тогда эпюра Мок



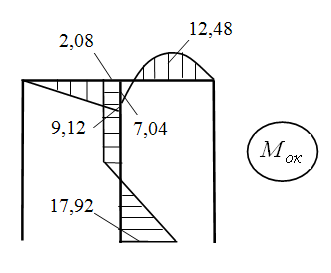
Проверки окончательной эпюры моментов (Мок).

1.Статическая проверка

---

 – методом вырезания жестких узлов рамы – они должны находиться в равновесии.



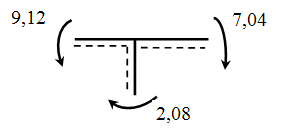
Узел находится в равновесии.

2. Деформационная проверка.



где МS – суммарная эпюра единичных моментов, для её построения одновременно к основной системе прикладываем Х1=1 и Х2=1.

Физический смысл деформационной проверки – перемещения по направлению всех отброшенных связей от действия неизвестных реакций и всей внешней нагрузки должны быть равны 0.

Строим эпюру МS .



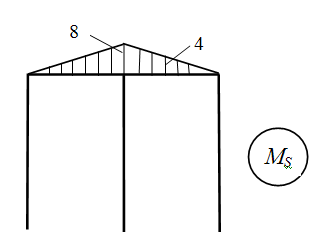
Выполняем деформационную проверку по ступеням:

6. 
   Построение Эп Q по Эп Мок.
   

Эп Q строим по формуле:



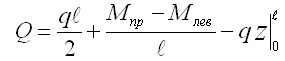
Если на участке нет равномерно-распределенной нагрузки, то применяем формулу:

---

,

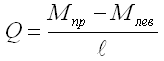
где Мпр – момент правый,

Млев – момент левый,

ℓ — длина участка.

Разобьем Эп Мок на участки:





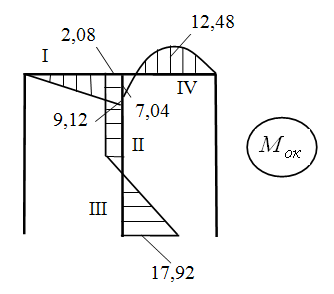
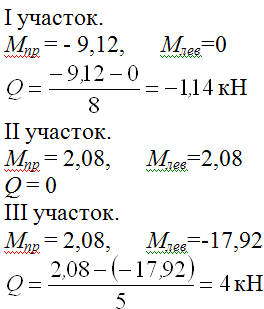
IV участок (с равномерно-распределенной нагрузкой).

Зарисуем IV участок отдельно как балку и нанесем моменты.



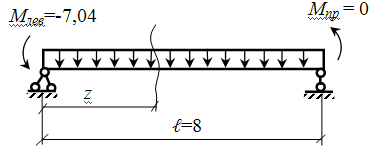
z меняется от 0 до ℓ



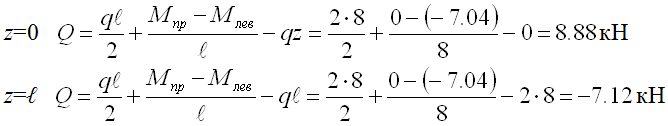
Строим ЭпQ:

7. 
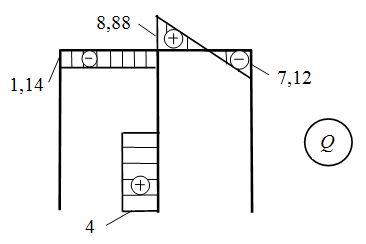
   Построение Эп N по Эп Q.
   

Вырезаем узлы рамы, показываем поперечные силы с эпюры Q и уравновешиваем узлы продольными силами.



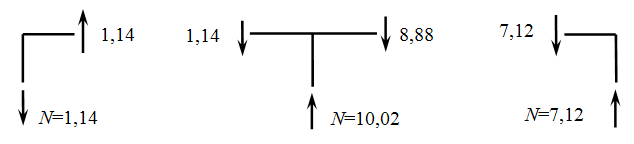
Строим Эп N.

8. 
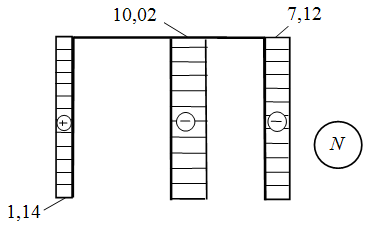
   Общая статическая проверка рамы. На заданной схеме рамы показываем значения опорных реакций с построенных эпюр  и проверяем по уравнениям статики.
   

---

Смотрите также файлы

• Измерение временной сложности алгоритма в эксперименте на эвм.docx

• Отчет по лабораторной работе 1 исследование линейных резистивных цепей.docx

• 2 поперечный профиль земляного полотна и его основные элементы 1 Назначение и типы земляного полотна.docx

• Курсовая работа по дисциплине Практические основы бухгалтерского учета источников формирования имущества организации.doc

• Отчет по производственной практике (научноисследовательской работе подготовительный этап).docx