ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования Республики Беларусь
Учреждение образования «Белорусский государственный университет
информатики и радиоэлектроники»
Институт информационных технологий
Факультет компьютерных технологий
Кафедра информационных систем и технологий
Контрольная работа №2
по дисциплине
«Алгоритмы и структуры данных»
Тема: «Ориентированные графы»
| | Выполнил студент группы 181074 Петрушенко Эльвира Алексеевна |
| | Проверил ассистент кафедры ИСиТ ИИТ БГУИР Потоцкий Дмитрий Сергеевич |
Минск 2023
Введение
Большинство задач на орграфах связаны с поиском заданных маршрутов на графе: кратчайшего, максимального и др. Решение многих таких задач опирается на алгоритмы Дейкстры и Флойда.
Определение центральной вершины орграфа выполняется через понятие эксцентриситет.
Центром орграфа G называется вершина с минимальным эксцентриситетом, т.е. это вершина, для которой максимальное расстояние (длина пути) до других вершин минимально.
Пусть есть ориентированный граф G=(V, E), у которого все дуги имеют неотрицательные метки, а одна вершина определена как источник. Задача состоит в нахождении стоимости кратчайших путей от источника ко всем другим вершинам граф G. Длина пути определяется как сумма стоимостей дуг, составляющих путь. Эта задача часто называется задачей нахождения кратчайшего пути с одним источником.
Для решения поставленной задачи будем использовать алгоритм Дейкстры. Алгоритм строит множество S вершин, для которых кратчайшие пути от источника уже известны. На каждом шаге к множеству S добавляется та из оставшихся вершин, расстояние до которой от источника меньше, чем для других оставшихся вершин. Если стоимости всех дуг неотрицательны, то кратчайший путь от источника к конкретной вершине проходит только через вершины множества
S. Такой путь называют особым. На каждом шаге алгоритма используется массив D, в который записываются длины кратчайших особых путей для каждой вершины. Когда множество S будет содержать все вершины орграфа, т.е. для всех вершин будут найдены особые пути, тогда массив D будет содержать длины кратчайших путей от источника к каждой вершине.
Нахождение путей между каждой парой вершин на орграфе выполняется с помощью алгоритма Флойда. Пусть дан орграф G=(V, E) и необходимо определить кратчайшие пути между всеми парами вершин орграфа. Каждой дуге
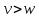этого графа сопоставлена неотрицательная стоимость C[v, w]. Общая задача нахождения кратчайших путей заключается в нахождении для каждой упорядоченной пары вершин (v, w) любого пути от вершины v в вершины w, длина которого минимальна среди всех возможных путей от v к w.Пронумеруем вершины графа последовательно от 1 доn.
Алгоритм Флойда использует матрицу А размера
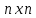в которой вычисляются длины кратчайших путей. Вначале А[i, j]=C[i, j] для всех i ≠ j. Если дуга 
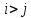отсутствует, то C[i, j]=∞. Каждый диагональный элемент матрицы А равен 0.Над матрицей А выполняется n итераций. После к-ой итерации А[i, j] содержит значение наименьшей длины путей из вершины i в вершинуj, которые не проходят через вершины с номером, большим к,т.е. между концевыми вершинами пути из i в j могут находиться только вершины, номера которых меньше или равны к. На к-ой итерации для вычисления матрицы А применяется следующая формула:
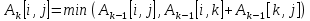
Цель работы: научиться обрабатывать элементы ориентированных графов, находить в них заданные маршруты.
Задание 1: Представить ориентированный граф
, состоящий из 7-10 вершин, с помощью матрицы смежности. Указать вершину-источник, а затем решить следующие задачи. Кратчайшие пути от вершины-источника до всех вершин орграфа на основе алгоритма Дейкстры.
Код программы:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace LR13
{
class Program
{
public class ShortestPathFinder
{
public ShortestPathFinder(int[,] matrix, int matrixSize)
{
Matrix = matrix;
MatrixSize = matrixSize;
}
private int[,] Matrix { get; }
private int MatrixSize { get; }
public void MatrixPrint()
{
Console.WriteLine("Ваша исходная матрица: ");
Console.WriteLine();
for (int i = 0; i < Matrix.GetLength(0); i++)
{
for (int j = 0; j < Matrix.GetLength(1); j++)
{
Console.Write("{0,3}", Matrix[i, j] + " ");
}
Console.WriteLine();
}
Console.WriteLine();
}
private int MinDistance(int[] dist, bool[] sptSet)
{
var min = int.MaxValue;
var minIndex = -1;
for (int i = 0; i < MatrixSize; i++)
{
if (sptSet[i] == false && dist[i] <= min)
{
min = dist[i];
minIndex = i;
}
}
return minIndex;
}
public void Dijkstra(int[,] matrix, int root)
{
var dist = new int[MatrixSize];
var path = new int[MatrixSize];
var checkPoint = new bool[MatrixSize];
for (int i = 0; i < MatrixSize; i++)
{
dist[i] = int.MaxValue;
checkPoint[i] = false;
}
dist[root] = 0;
for (int i = 0; i < MatrixSize - 1; i++)
{
var minDist = MinDistance(dist, checkPoint);
checkPoint[minDist] = true;
for (int j = 0; j < MatrixSize; j++)
{
if (!checkPoint[j] && matrix[minDist, j] != 0 && dist[minDist] != int.MaxValue && dist[minDist] + matrix[minDist, j] < dist[j])
{
dist[j] = dist[minDist] + matrix[minDist, j];
path[j] = minDist;
}
}
}
Console.WriteLine("Данные о путях(по Дейкстре):");
Console.WriteLine();
Console.WriteLine($"Наша начальная точка 1");
for (int i = 1; i < MatrixSize; i++)
{
if (path[i] == 0)
Console.WriteLine($"Кратчайший путь: из 1 -> {i + 1} прямой; Мин.Расстояние: {dist[i]}");
else
{
var stack = new Stack
stack.Push(path[i] + 1);
Console.Write($"Кратчайший путь: из 1 -> ");
for (int j = path[i]; j != 0; j = path[j])
{
if (path[j] == 0)
break;
else
{
stack.Push(path[j]);
j = path[j];
}
}
for (int j = 0; j <= stack.Count; j++)
{
if (j == stack.Count)
Console.Write($"{i + 1}; Мин.Расстояние: {dist[i]}");
else
{
Console.Write(stack.Pop() + " -> ");
j = -1;
}
}
Console.WriteLine();
}
}
}
}
static void Main(string[] args)
{
int[,] graph = {
{ 0, 6, 0, 0, 0, 0, 0, 9, 0 },
{ 6, 0, 9, 0, 0, 0, 0, 11, 0 },
{ 0, 9, 0, 5, 0, 6, 0, 0, 2 },
{ 0, 0, 5, 0, 9, 16, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 6, 0, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 16, 0, 2, 0, 1, 6 },
{ 9, 11, 0, 0, 0, 0, 1, 0, 5 },
{ 0, 0, 2, 0, 0, 0, 6, 5, 0 }
};
ShortestPathFinder finder = new ShortestPathFinder(graph, 9);
finder.Dijkstra(graph, 0);
Console.ReadKey();
}
}
}
Результат работы программы:
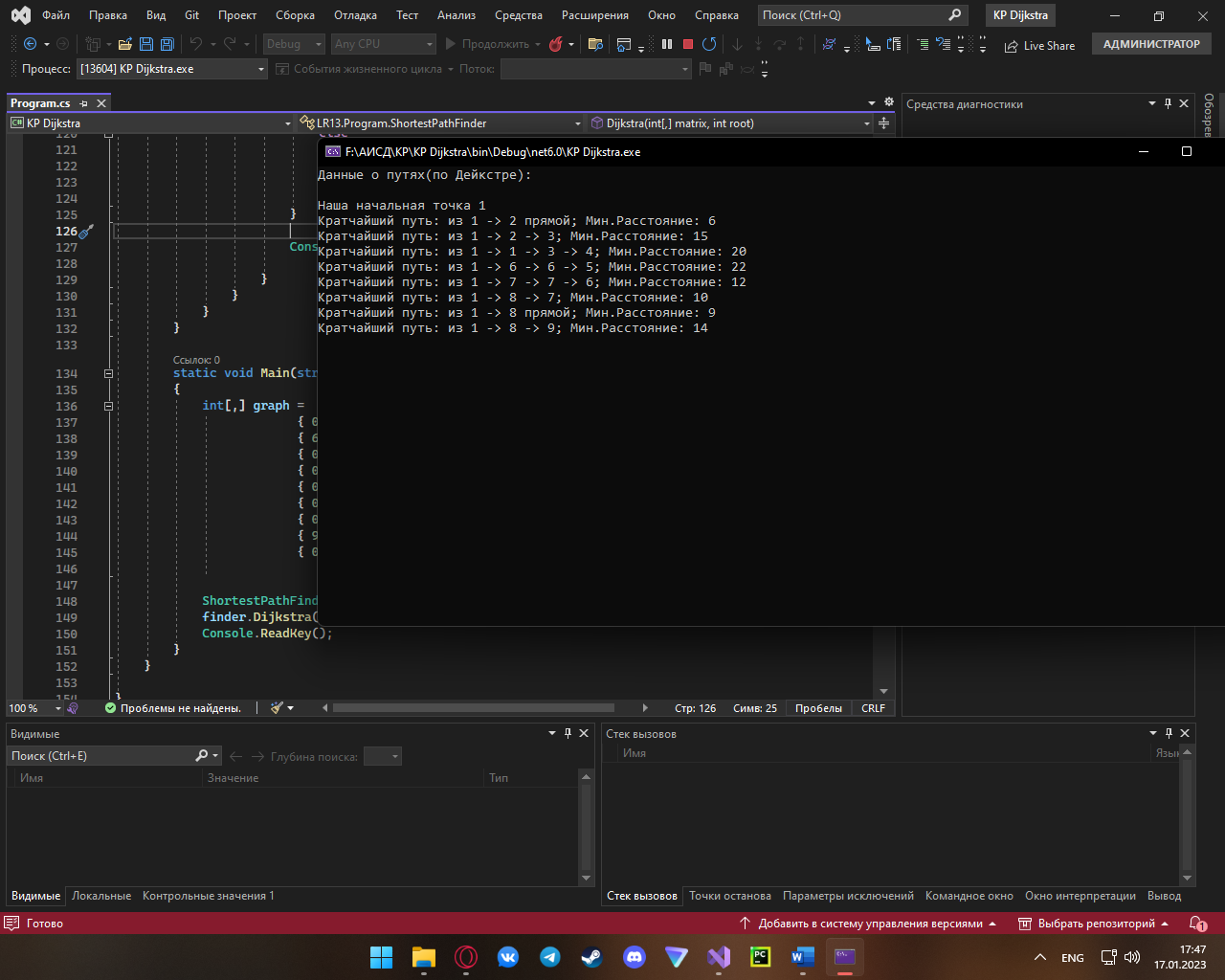
Задание 2: Представить ориентированный граф, состоящий из 7-10 вершин, с помощью матрицы смежности. Указать вершину-источник, а затем решить следующие задачи. Кратчайшие расстояния между каждой парой вершин орграфа на основе алгоритма Флойда.
Код программы:
#include
#define INF 9000000
#define MatrixLen 5
int main()
{
int matrix[MatrixLen][MatrixLen] =
{
{0, 5, 2, INF, INF},
{5, 0, INF, 7, INF},
{2, INF, 0, 2, 8},
{INF, 7, 2, 0, 1},
{INF, INF, 8, 1, 0}
};
for (size_t k(0); k < MatrixLen; ++k) {
for (size_t i(0); i < MatrixLen; ++i) {
for (size_t j(0); j < MatrixLen; ++j) {
if (matrix[i][k] < INF && matrix[k][j] < INF) {
if (matrix[i][k] + matrix[k][j] < matrix[i][j]) {
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
}
}
}
}
for (int i = 0; i < MatrixLen; i++)
{
int from = i;
for (int j = 0; j < MatrixLen; j++)
{
int to = j;
std::cout << "Path length from " << from << " to " << to << " is " << matrix[from][to] << std::endl;
}
}
}
Результат выполнения программы:
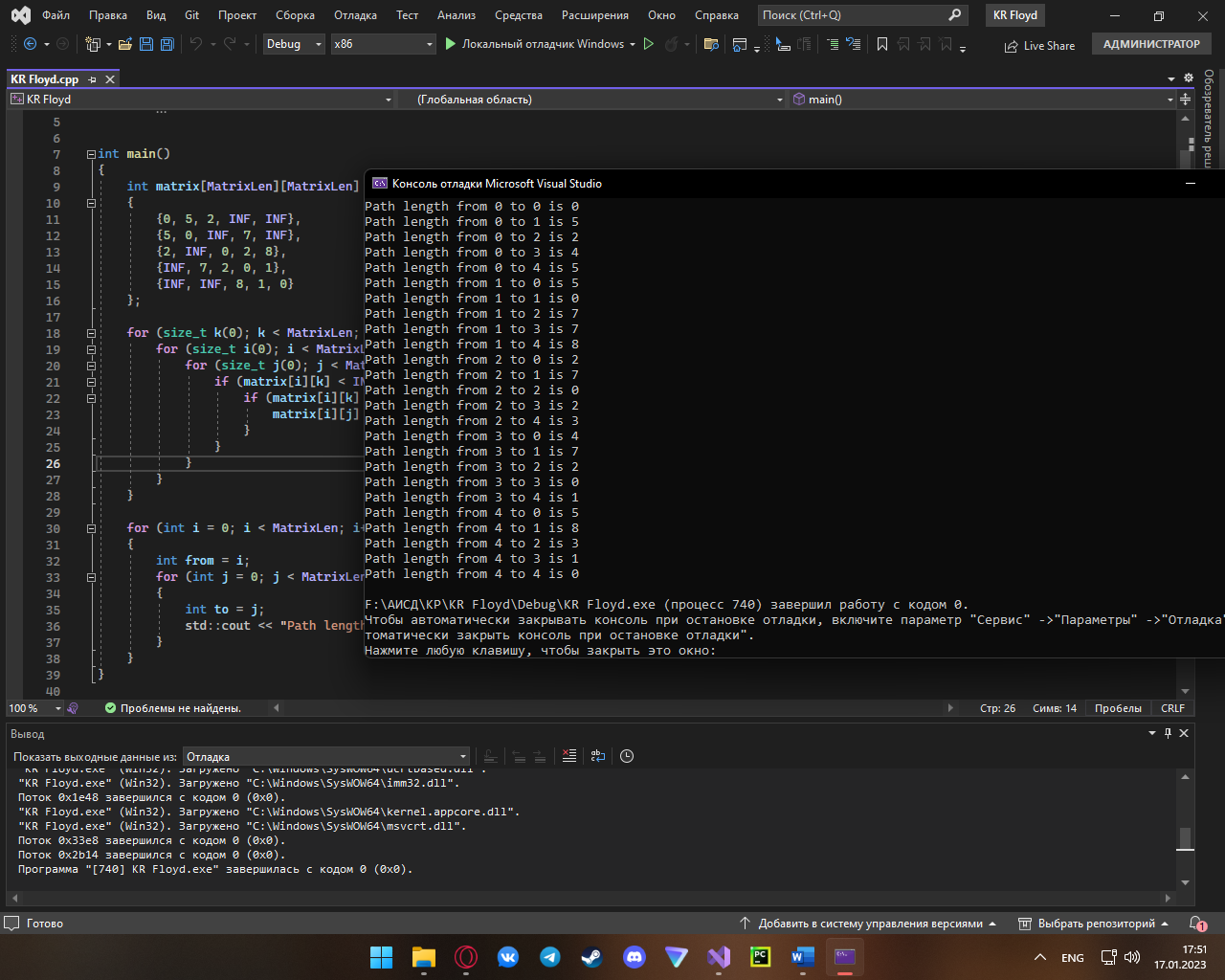
Контрольные вопросы и задания:
-
Для решения какой задачи на ориентированном графе удобно использовать алгоритм Дейкстры?
Алгоритм Дейкстры работает на ориентированных (с некоторыми дополнениями и на неориентированных) графах, и призван искать кратчайшие пути между заданной вершиной и всеми остальными вершинами в графе.
Алгоритм Дейкстры может найти кратчайший путь между вершинами в графе, только если существует хотя бы один путь между этими вершинами. Если это условие не выполняется, то алгоритм отработает корректно, вернув значение "бесконечность" для пары несвязанных вершин.
-
Для решения какой задачи на ориентированном графе удобно использовать алгоритм Флойда?
Алгоритм Флойда — Уоршелла — алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного графа без циклов с отрицательными весами.
Если граф не содержит рёбер с отрицательным весом, то для решения этой проблемы можно использовать алгоритм Дейкстры для нахождения кратчайшего пути от одной вершины до всех остальных, запустив его на каждой вершине.
Если же есть рёбера с отрицательным весом, можно использовать алгоритм Беллмана — Форда. Но этот алгоритм, запущенный на всех вершинах графа, медленнее, время его работы O(V2*E), а в сильно «густых» графах аж O(V4).
-
Какая вершина графа называется его центром?
Центром называется вершина н-графа, от которой максимальное из расстояний до других вершин являлось бы минимальным.
Заключение
В ходе проделанной контрольной работы были изучены ориентированные графы, работа с ними и нахождение кратчайших путей по графам при помощи алгоритмов Дейкстры и Флойда. Были реализованы данные алгоритмы на языках С# и C++.