Файл: Контрольная работа 1 Задание 10 Вычислить определители а, б. Решение а. б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 102
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
е) составить квадратное уравнение с действительными коэффициентами, корнем которого является :
: 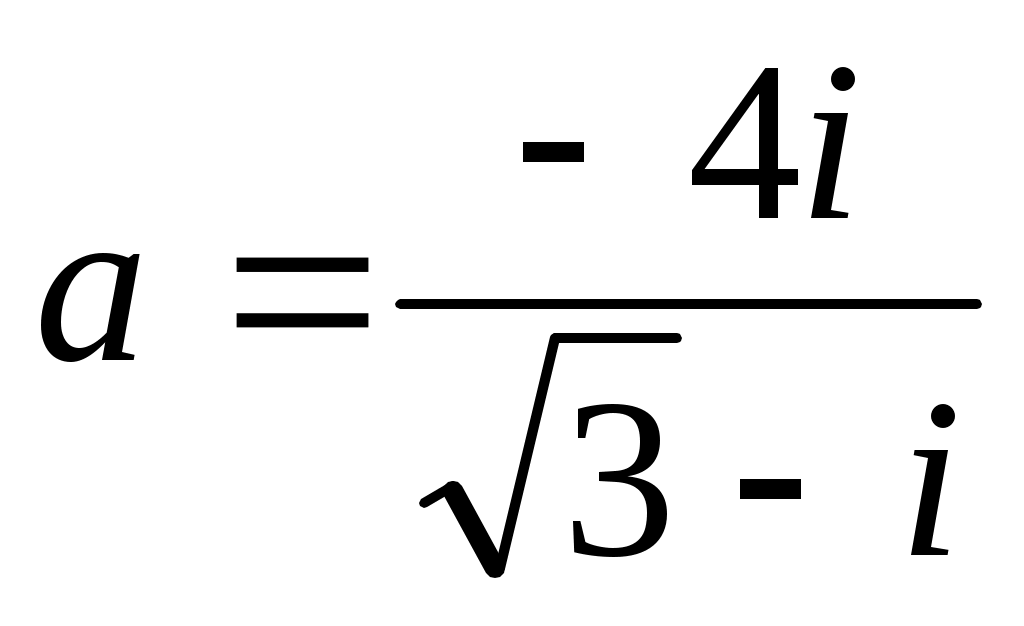 .
.
Решение
а) Умножим числитель и знаменатель на сопряжённый знаменателю множитель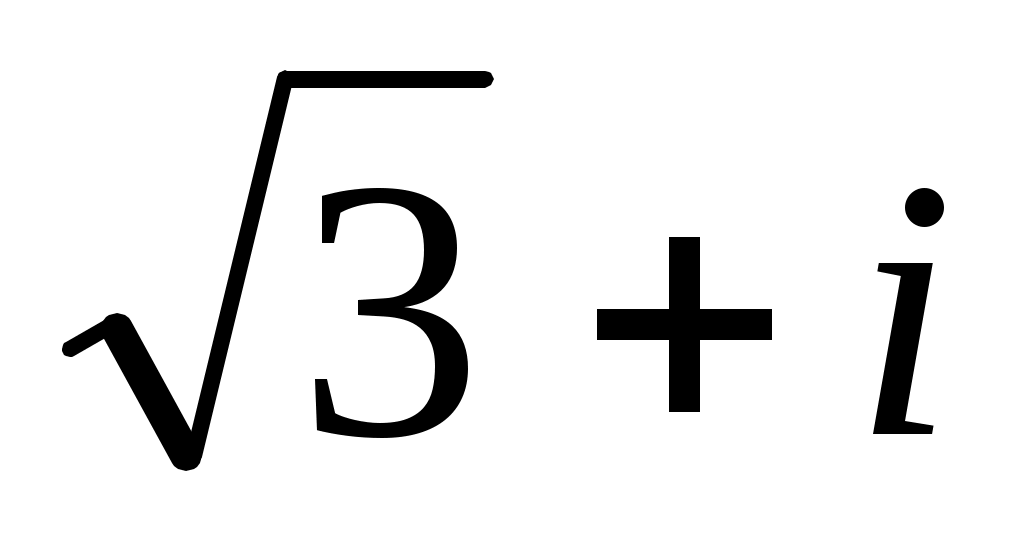 :
:
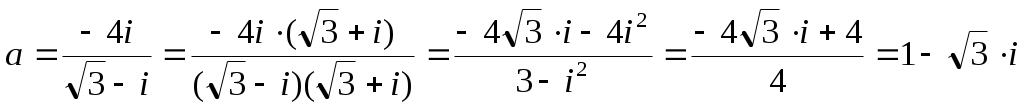 -
-
алгебраическая форма комплексного числа.
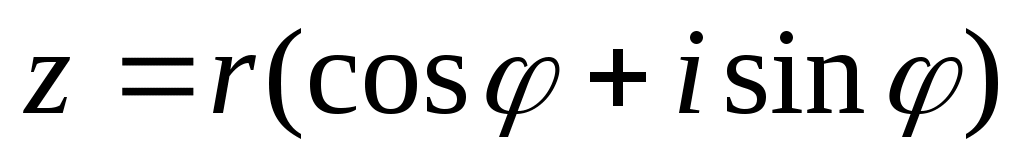 , где
, где 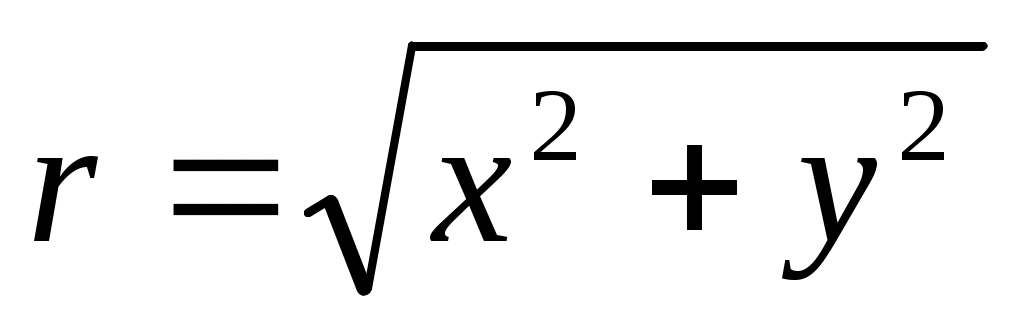 , у нас
, у нас 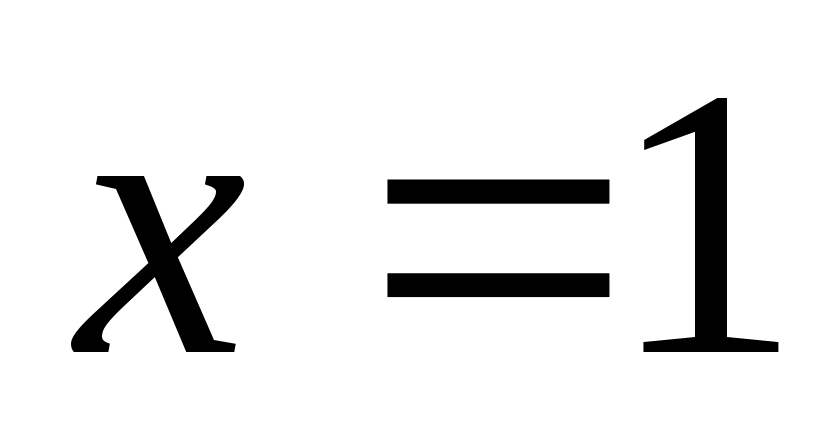 ,
, 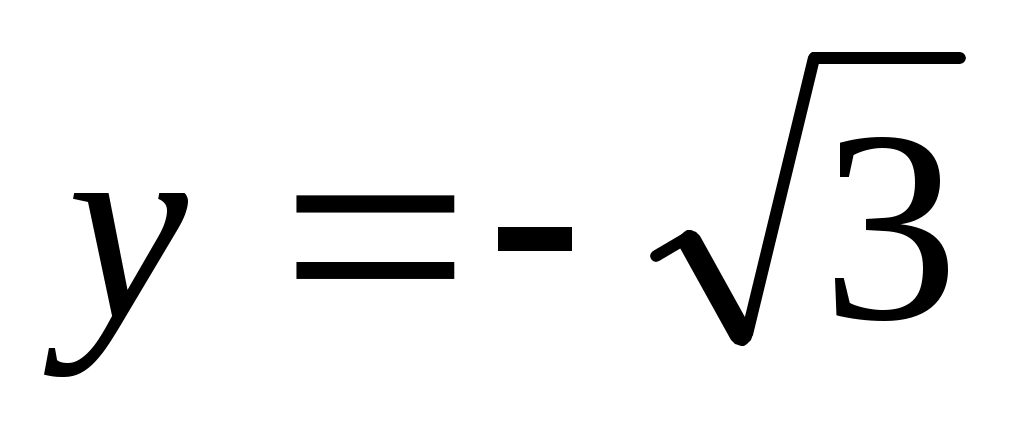 .
.
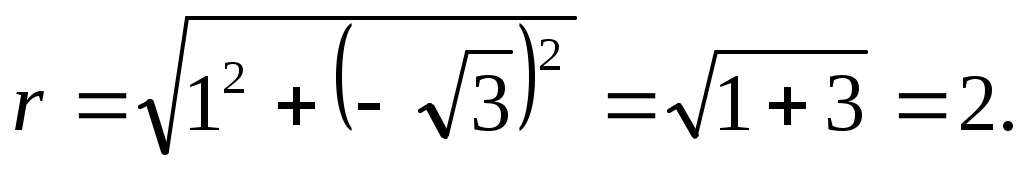 Анализируем аргумент, чтобы определить угол. Так как
Анализируем аргумент, чтобы определить угол. Так как 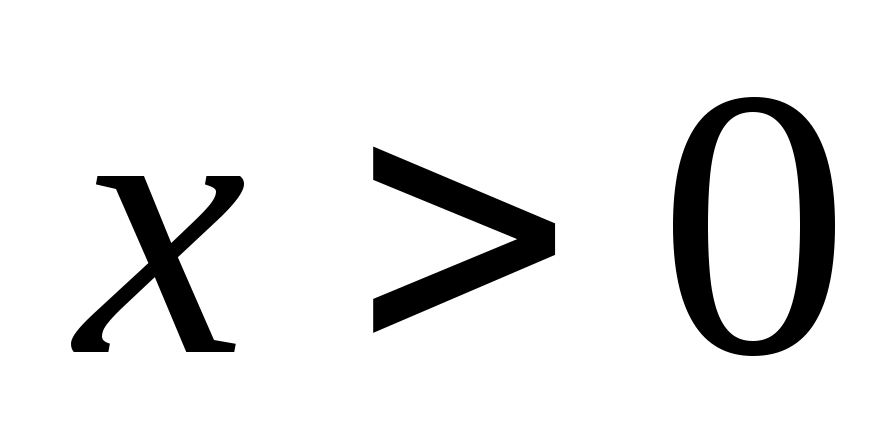 и
и 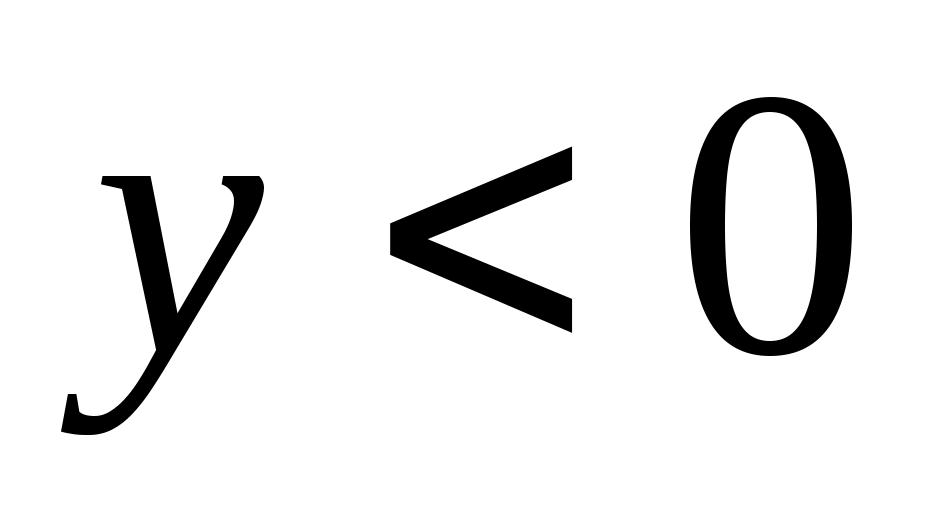 , то
, то
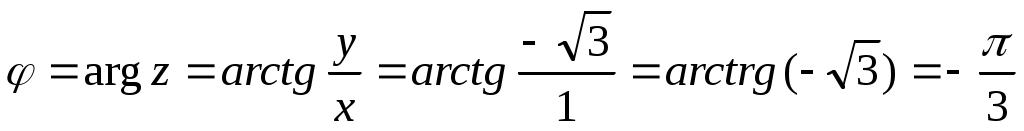 .
.
Окончательно, получим тригонометрическую формулу данного числа: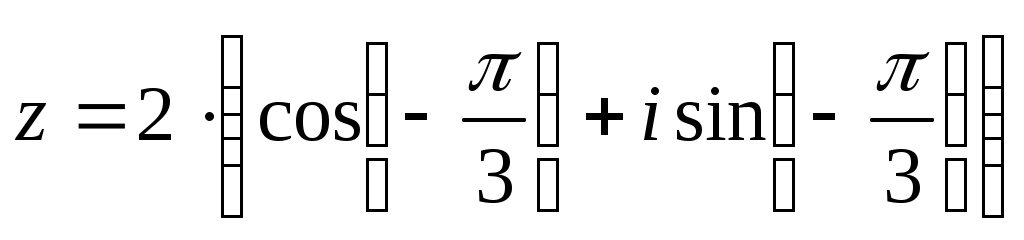 .
.
Показательная форма комплексного числа: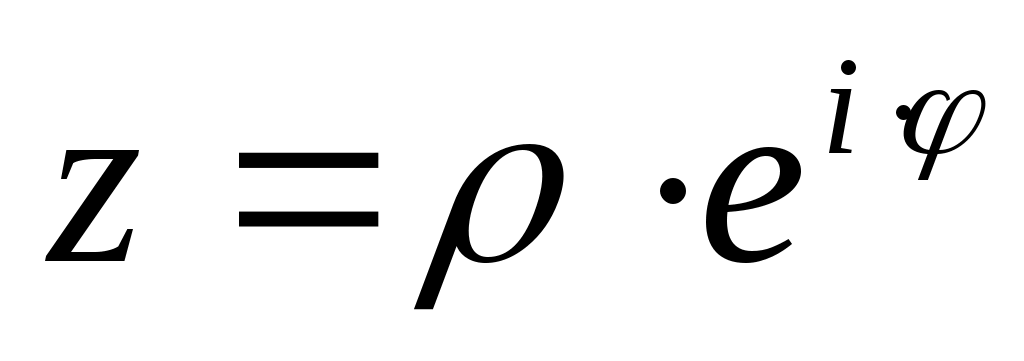 , тогда
, тогда 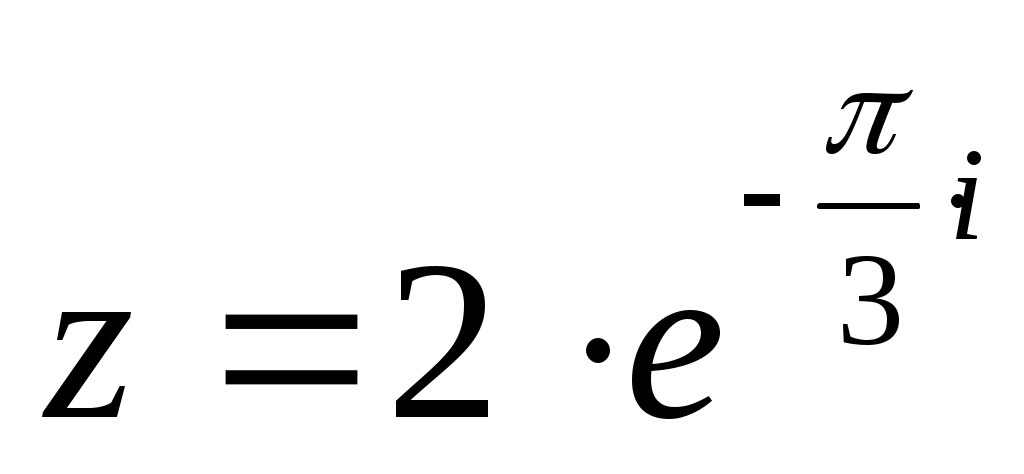 .
.
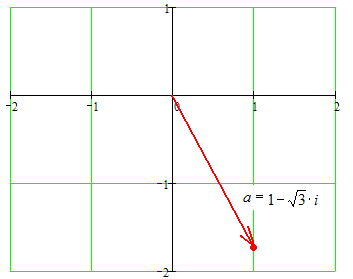
б) Изобразим это число на комплексной плоскости:
в) Применим формулу: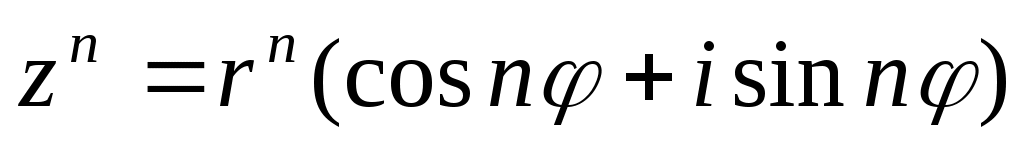 .
.
Мы нашли тригонометрическую форму заданного числа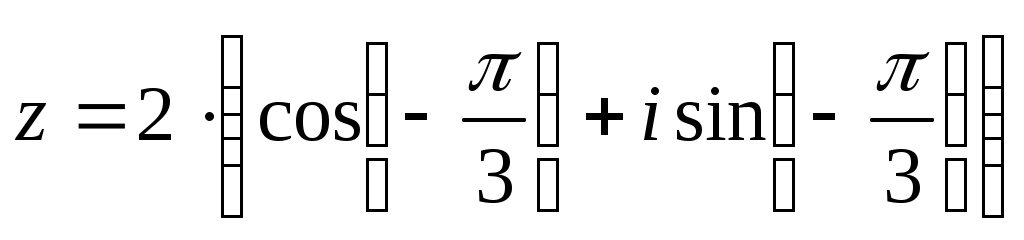 , тогда
, тогда
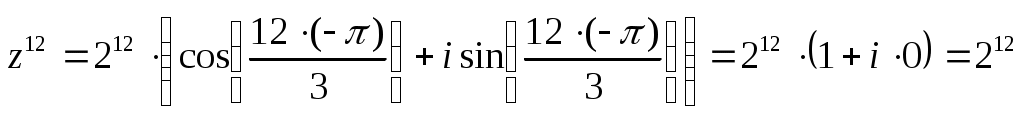 .
.
г) Найдём корни уравнения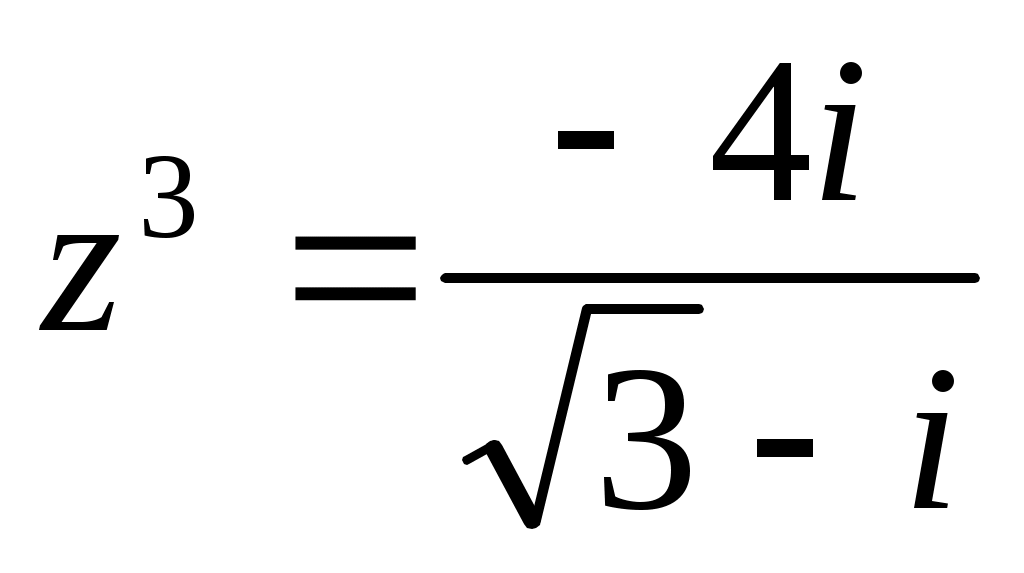 .
.
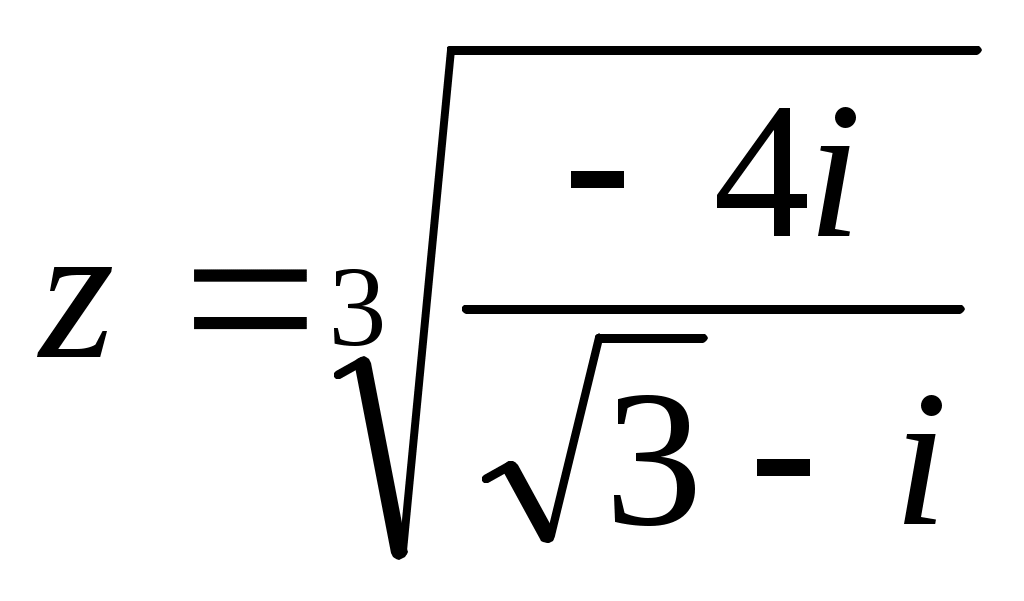 .
.
Для извлечения корня применим формулу:
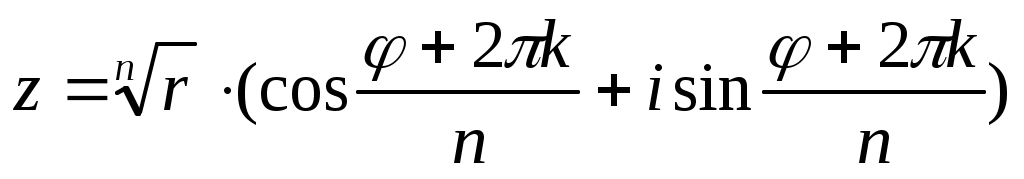 , где
, где 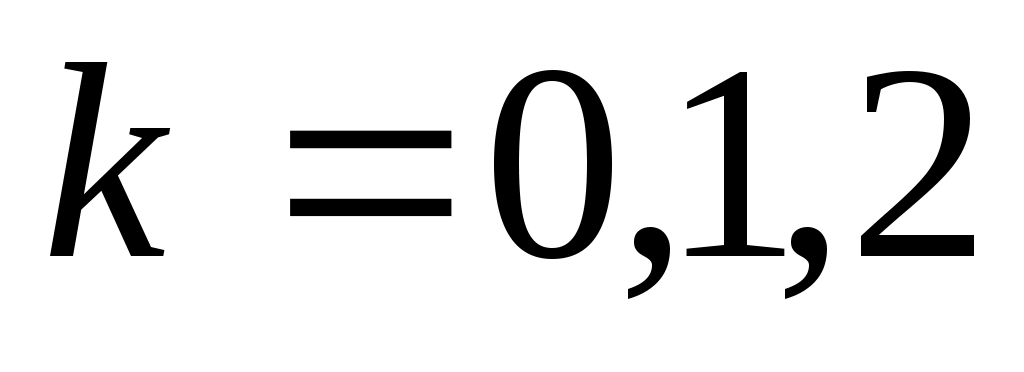 .
.
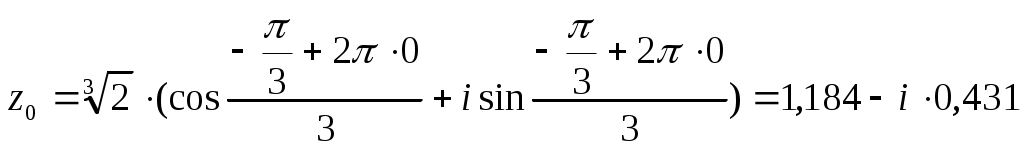 ,
,
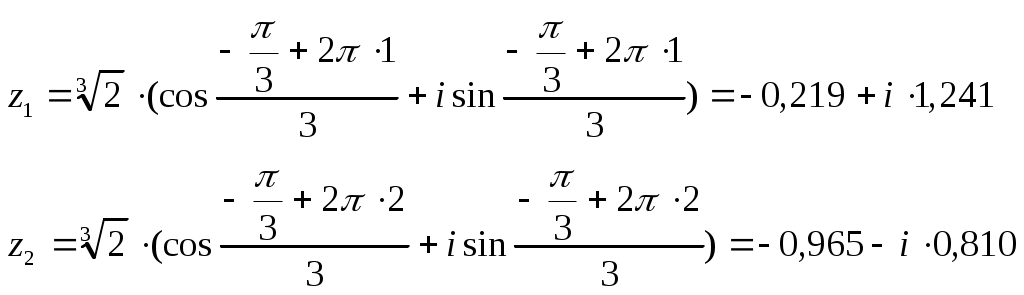
д) Вычислим произведение полученных корней.
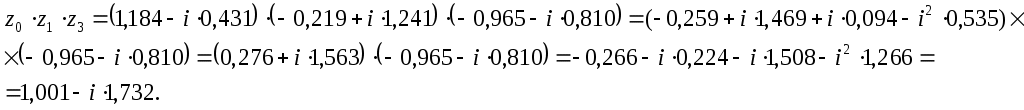
е) Составим квадратное уравнение с действительными коэффициентами, корнем которого является :
: 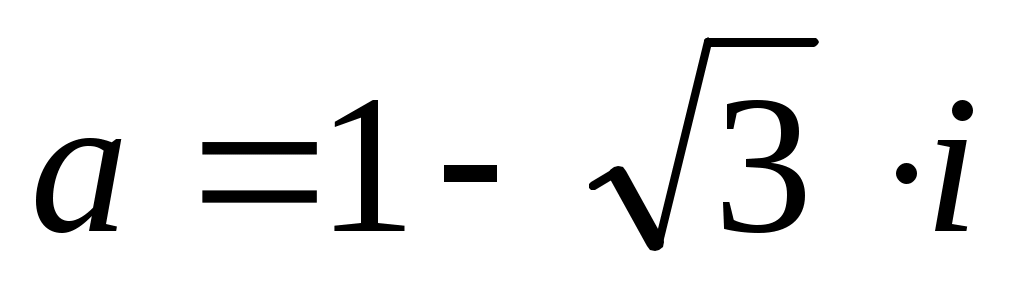 .
.
Квадратное уравнение имеет вид: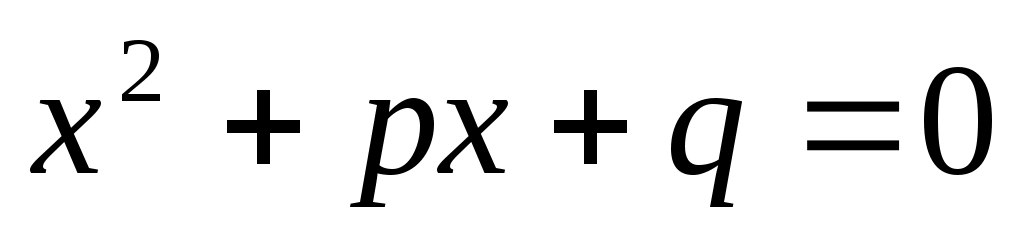 . Вспоминая теорему Виета, запишем
. Вспоминая теорему Виета, запишем
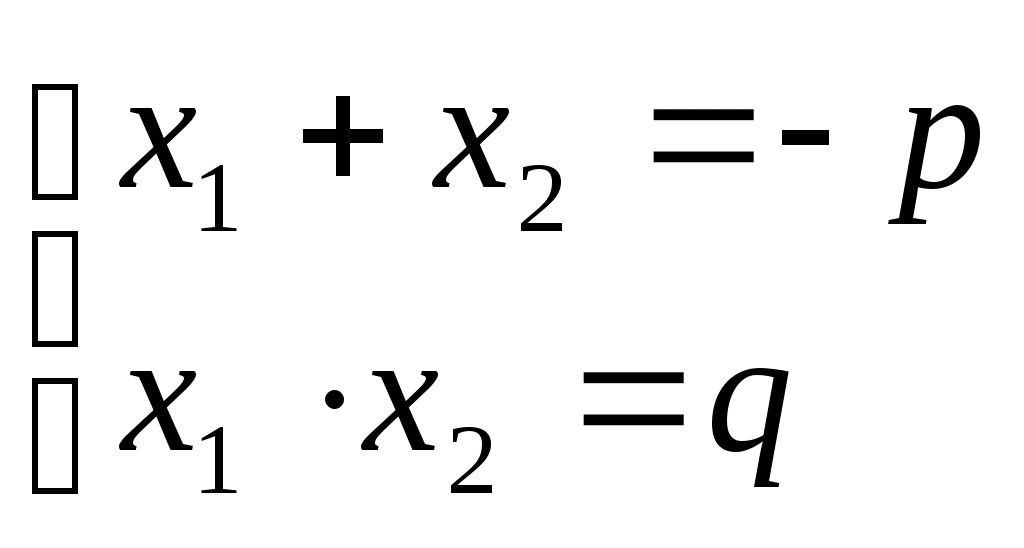
Один из корней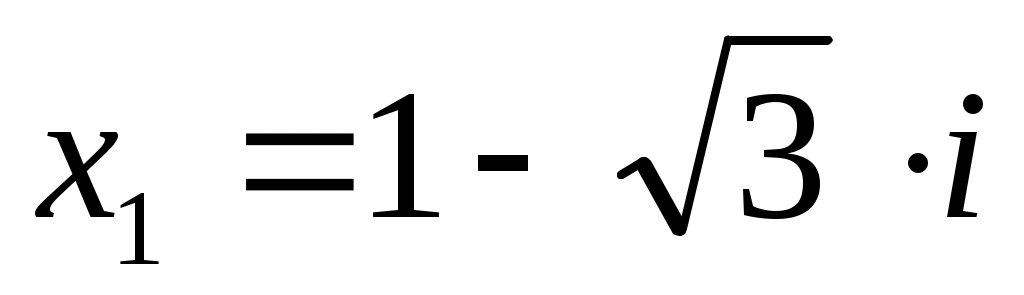 , значит, второй равен
, значит, второй равен 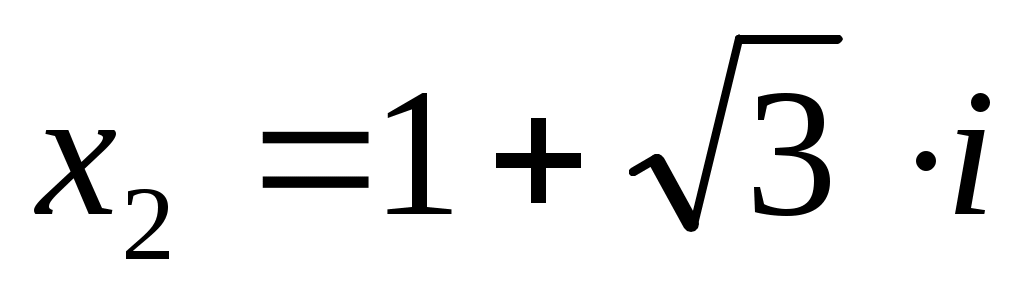 . Тогда,
. Тогда,
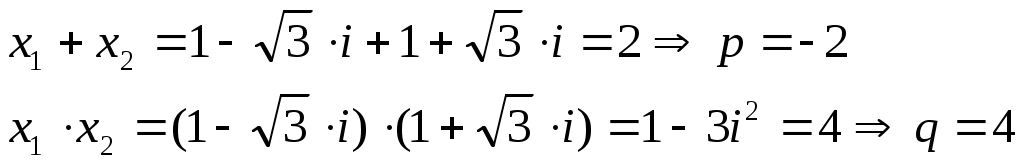
Тогда, квадратное уравнение примет вид: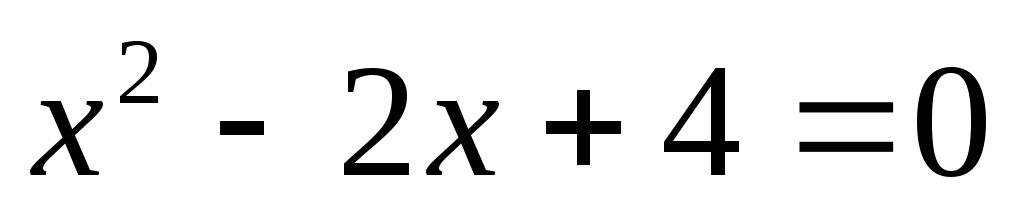 .
.
Контрольная работа 2
Задание 2.10
Найти длину вектора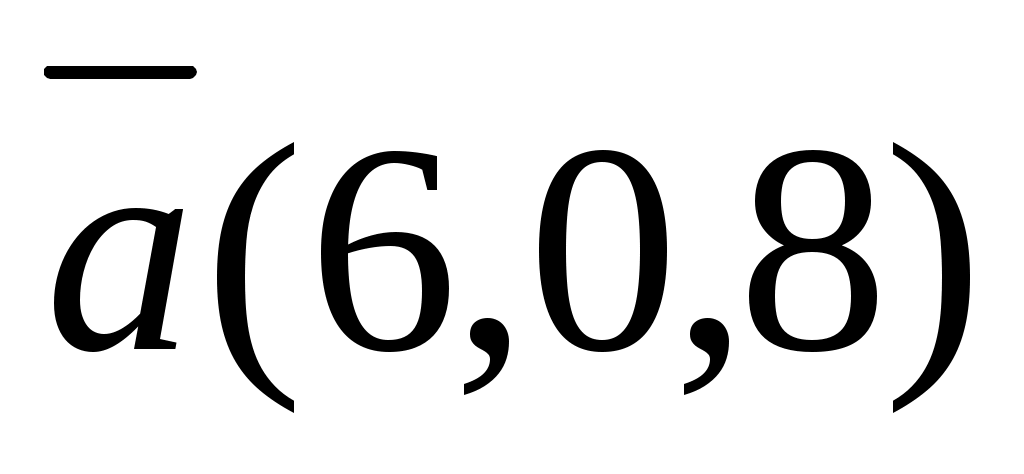 и
и 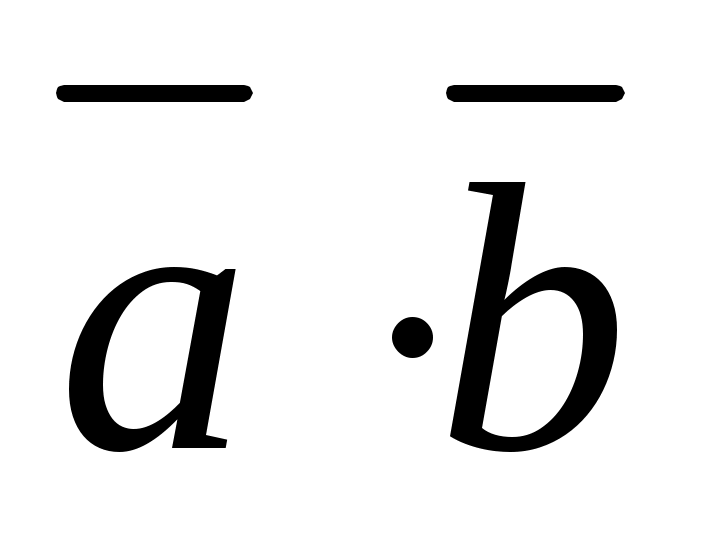 , где
, где 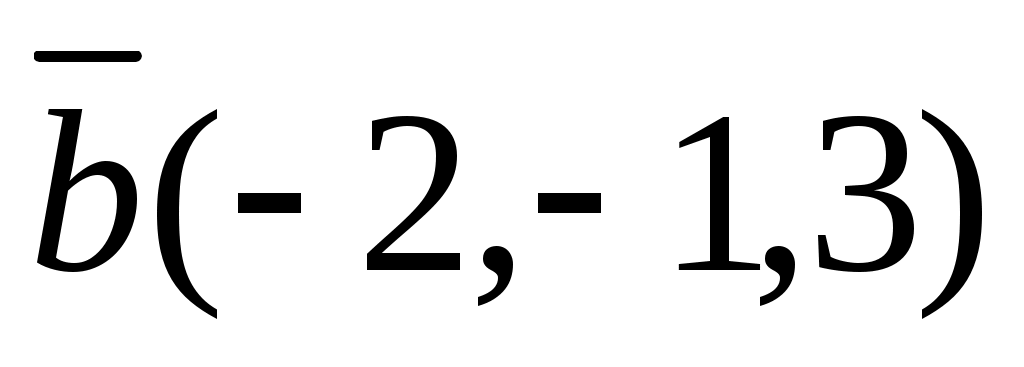 .
.
Решение
Найдём длину вектора:
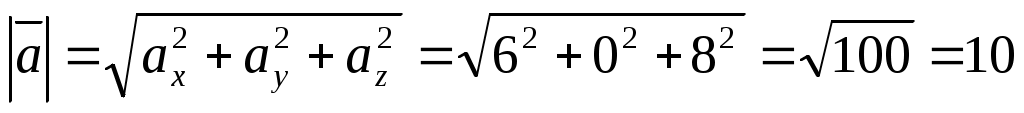 .
.
Найдём скалярное произведение:
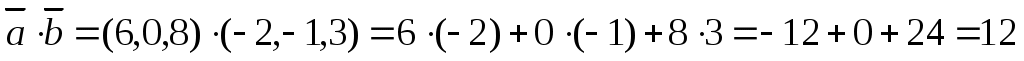
Задание 2.20
Написать уравнение плоскости, проходящей через точки M, K и L в виде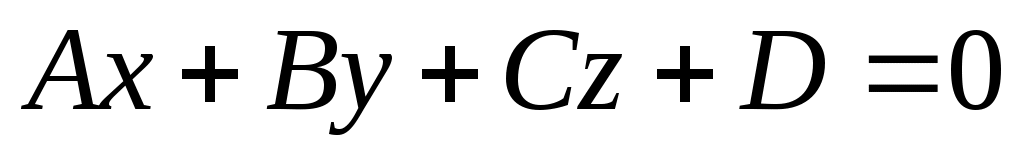 .
.
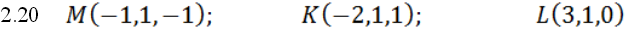
Решение
Уравнение плоскости ищем в виде:
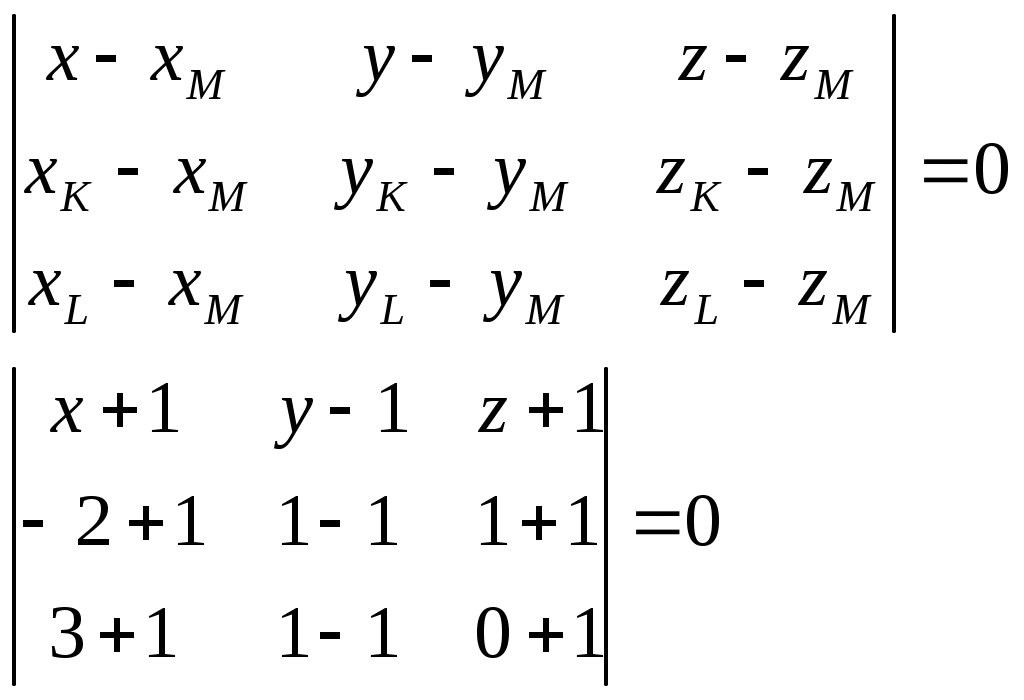
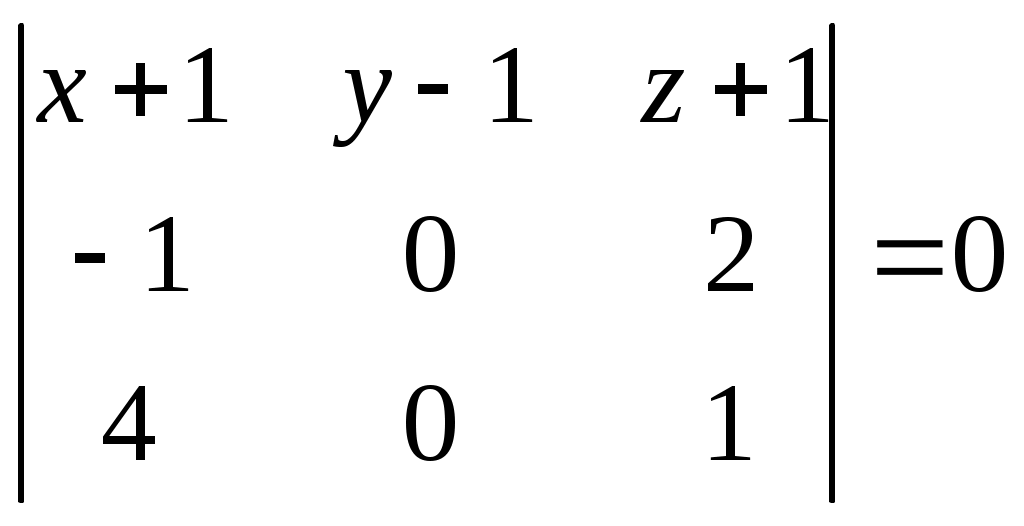
Раскроем определитель по элементам второго столбца:
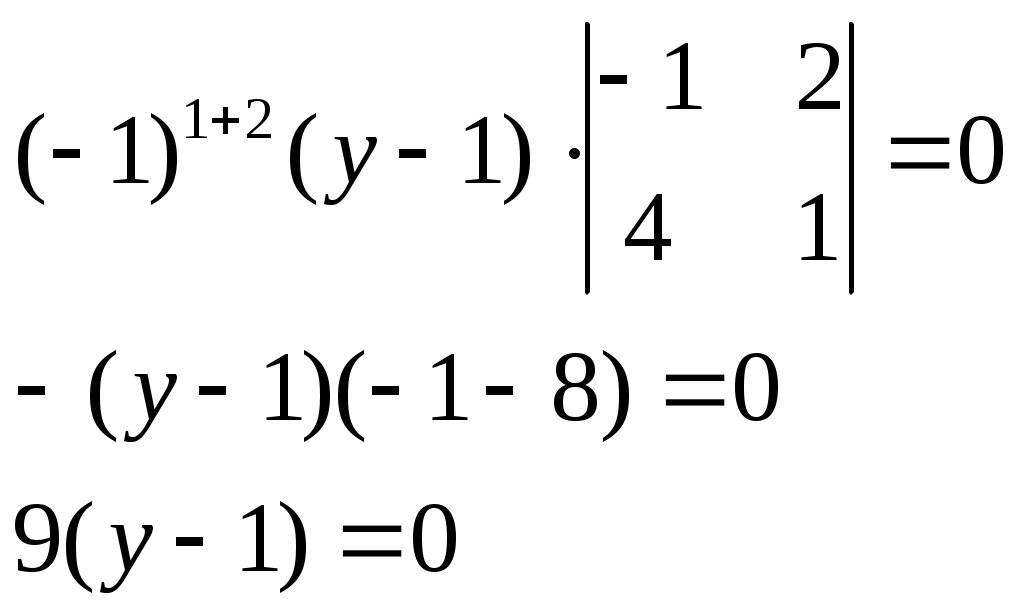
Следовательно, уравнение плоскости: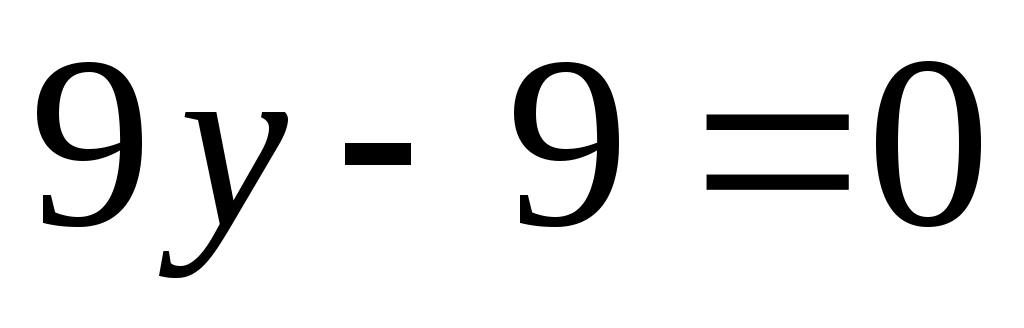
Задание 2.30
Даны 4 вектораa,b,c,d.
a(7, -10, -4); b(2, -8, -4); c(-6, 16, 7); d(11, -13, -5);
Вычислить:
1) координаты вектораd в базисе a,b,c;
2) a .b ;
3) с .d ;
4) (2a + 3b ) . (5c – 4d);
5) a b ;
6) с d ;
7) (a с ) .d .
Решение
1. Разложение вектора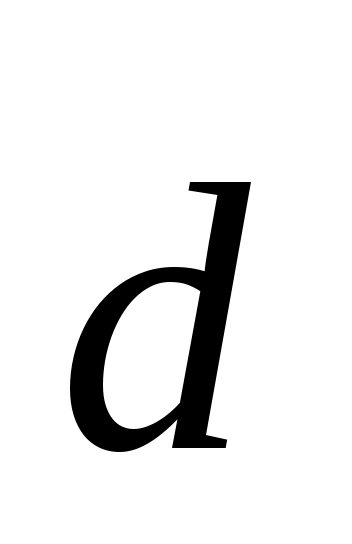 в базисе имеет вид:
в базисе имеет вид: 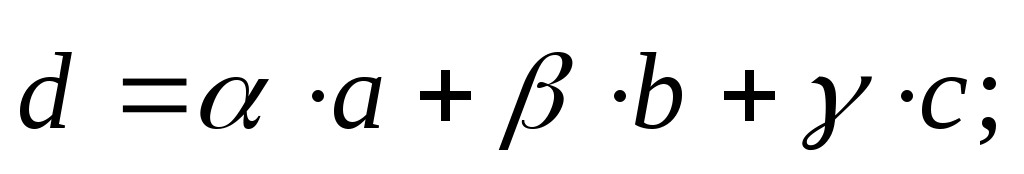 это векторное уравнение относительно
это векторное уравнение относительно 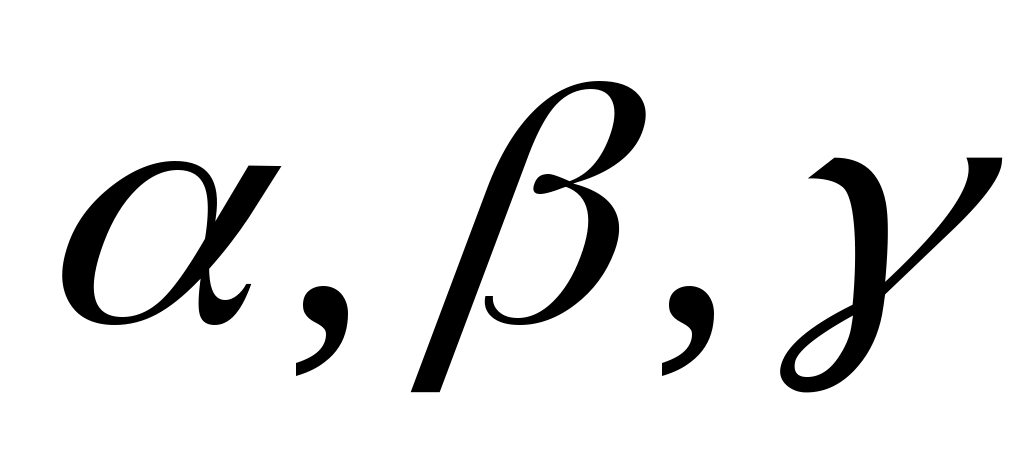 , которое эквивалентно системе трёх линейных уравнений с тремя неизвестными.
, которое эквивалентно системе трёх линейных уравнений с тремя неизвестными.
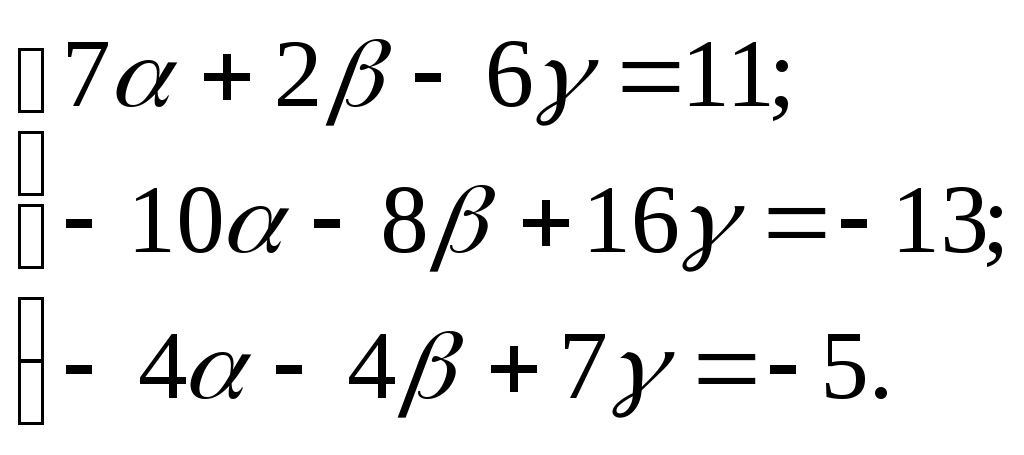
Найдём главный определитель системы:
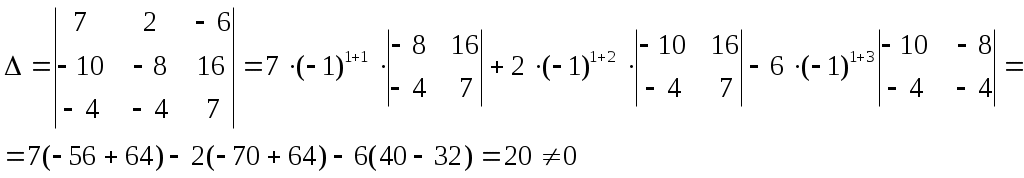
Так как определитель отличен от нуля, то векторы некомпланарные, линейно независимые, а значит, образуют базис. Значит, данная система имеет единственное решение, которое мы найдём по формулам Крамера:
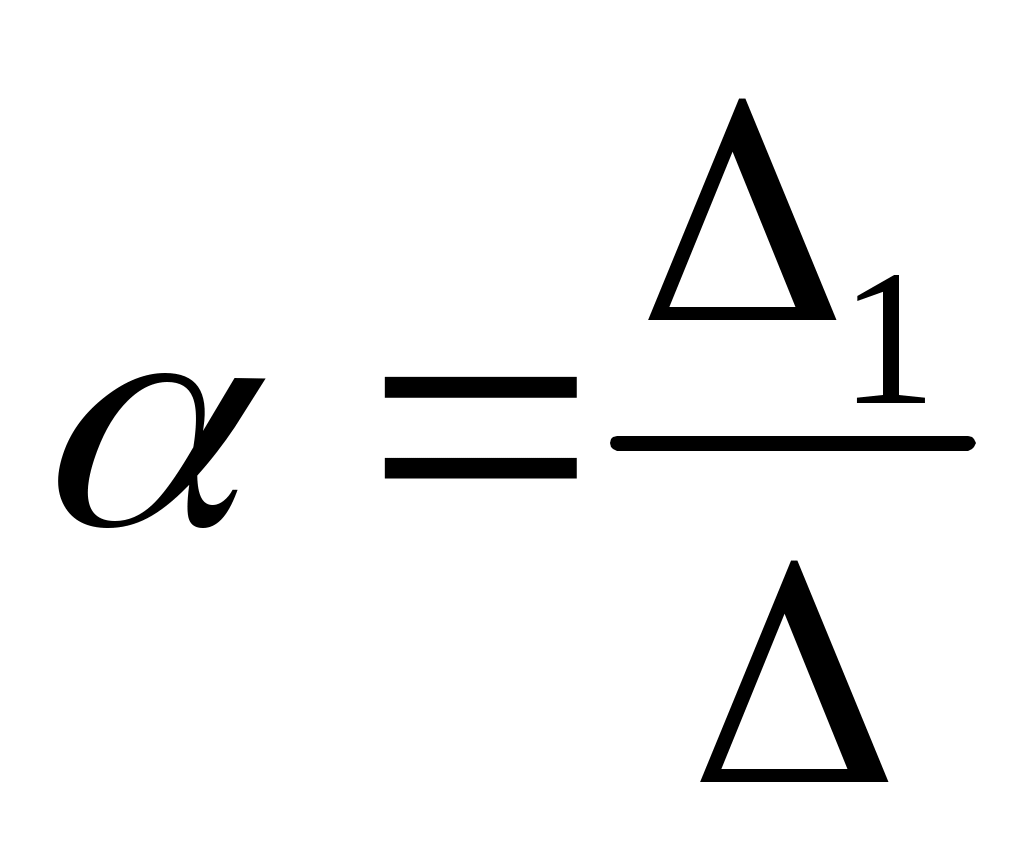 ,
, 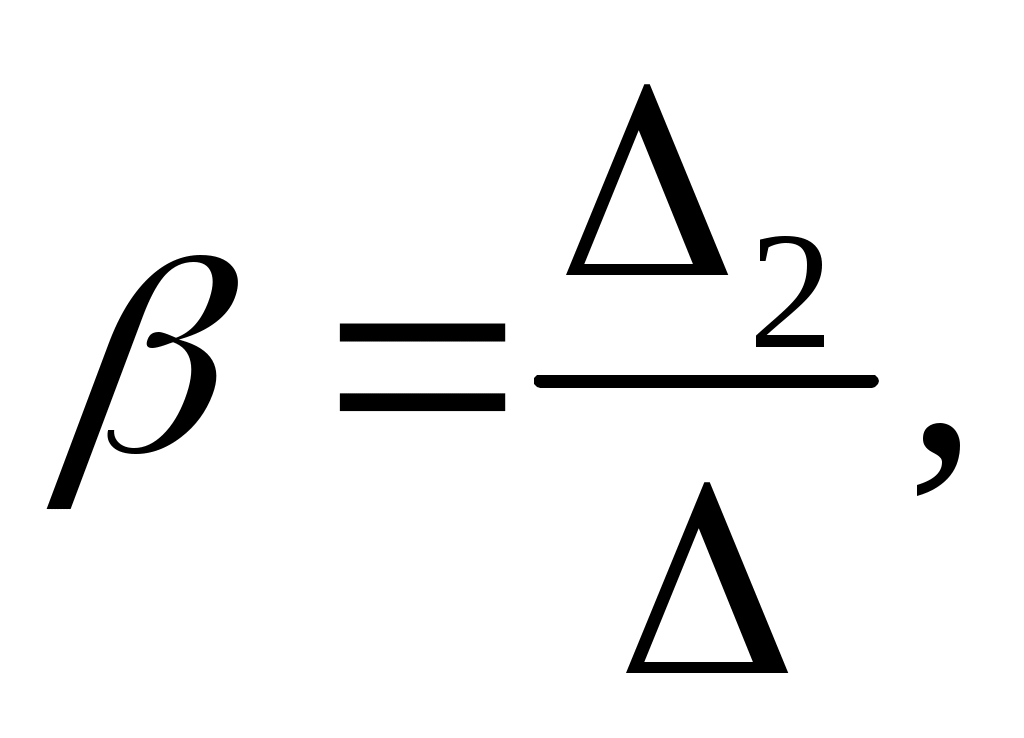
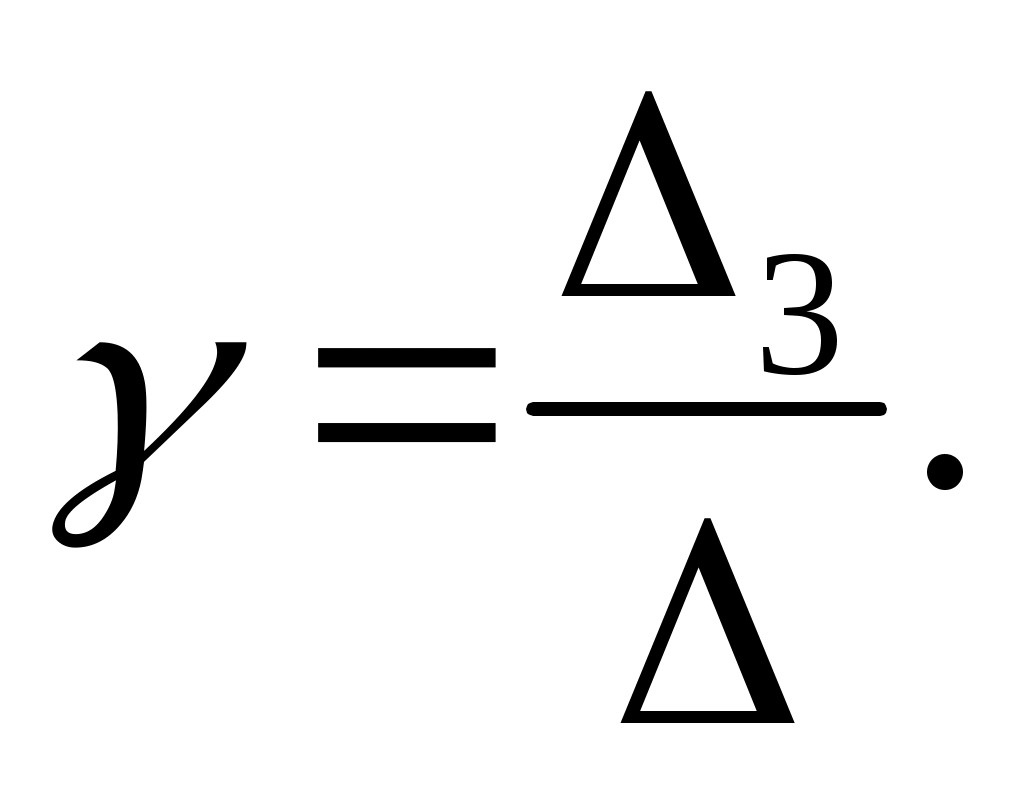
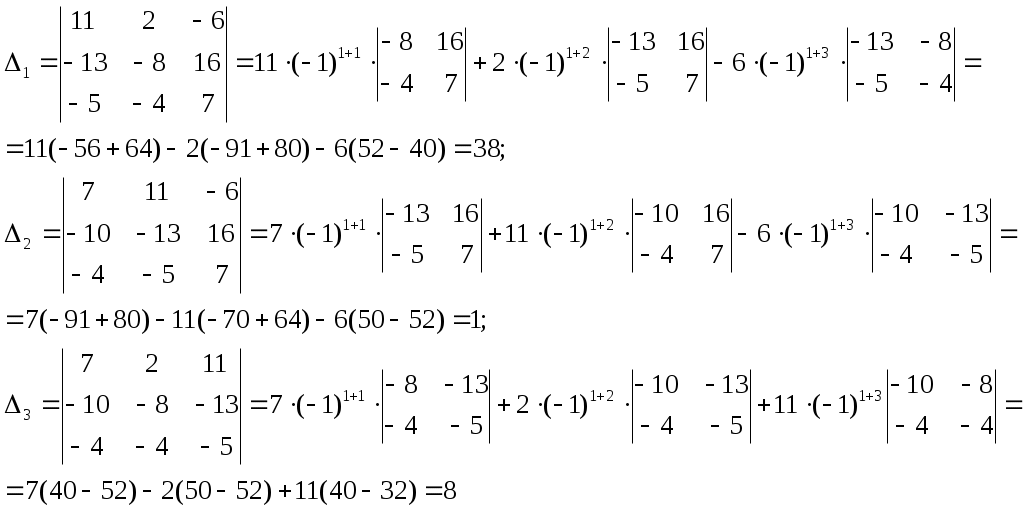
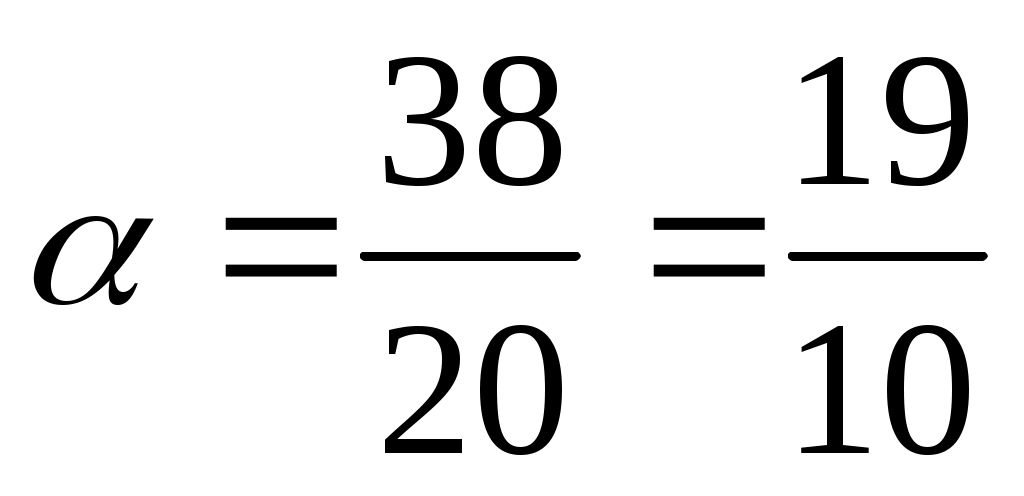 ,
, 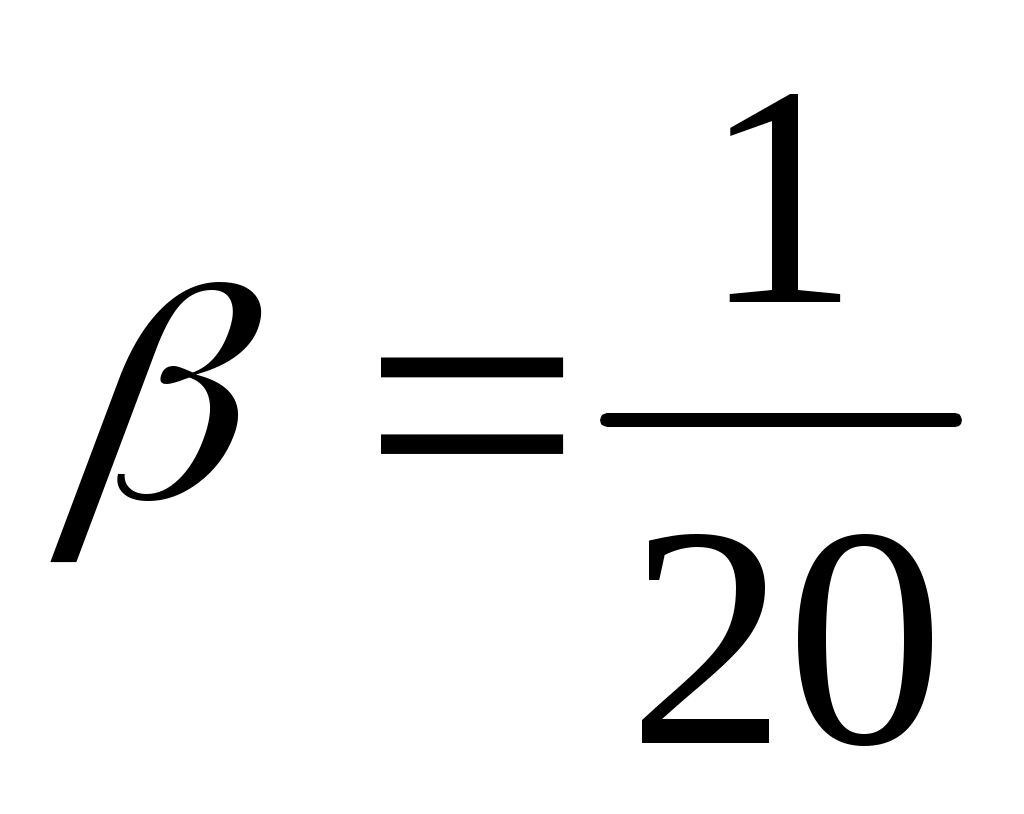
,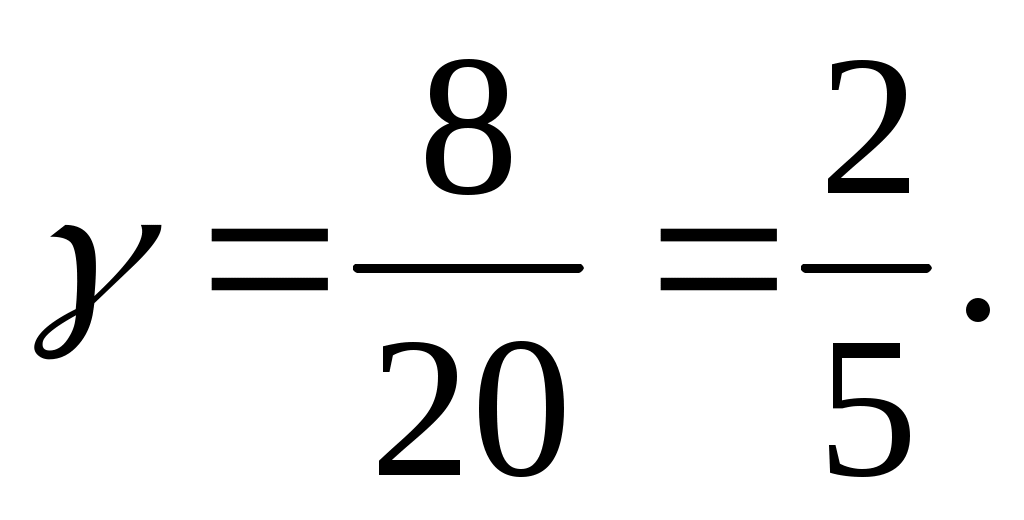
Таким образом,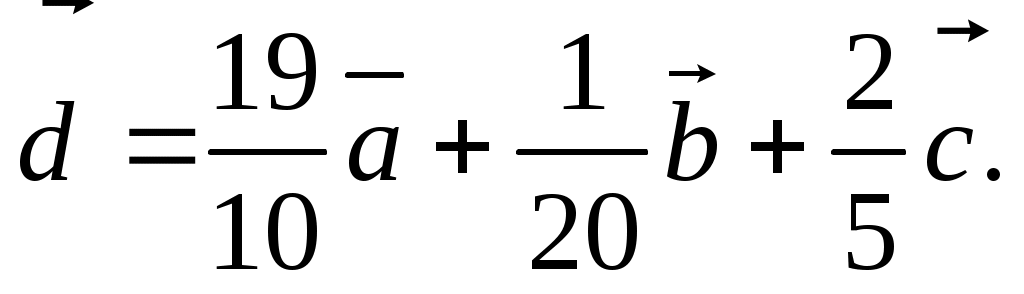
2. Найдём скалярное произведение двух векторов: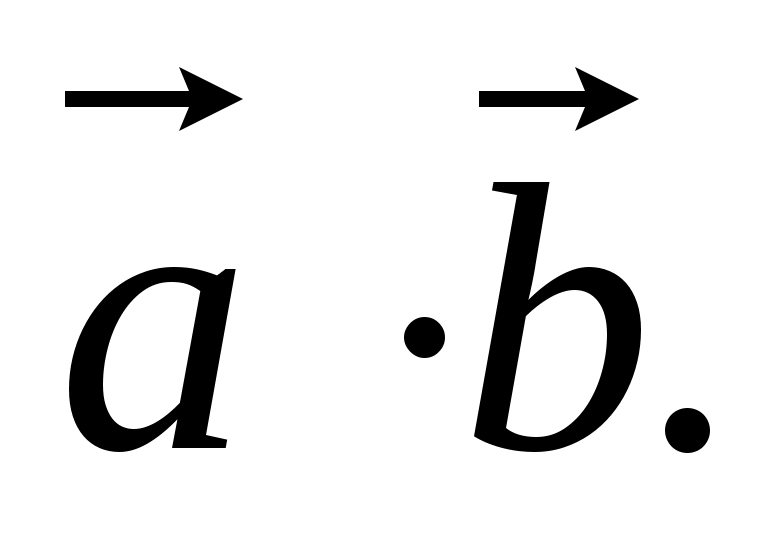
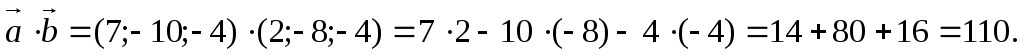
3. Найдём скалярное произведение двух векторов: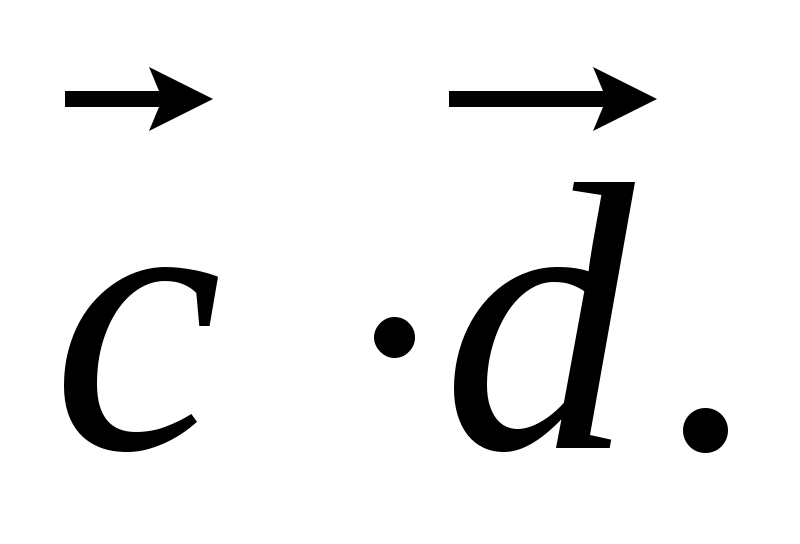
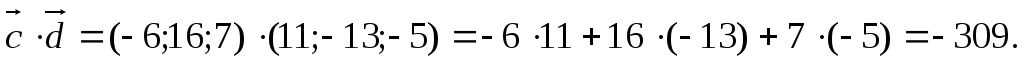
4.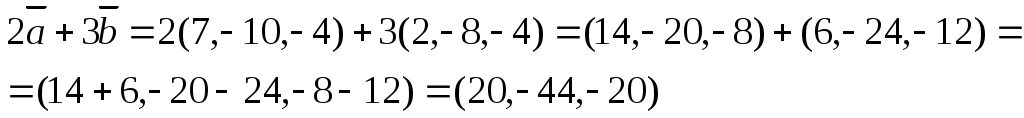
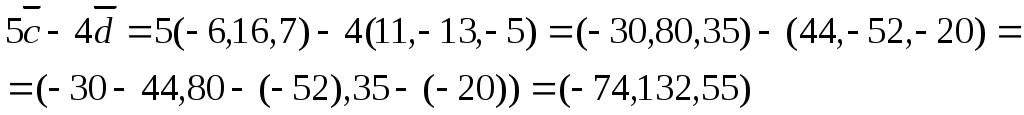
Найдём скалярное произведение:
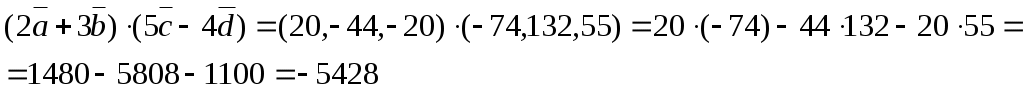
5. Найдём векторное произведениеa b;
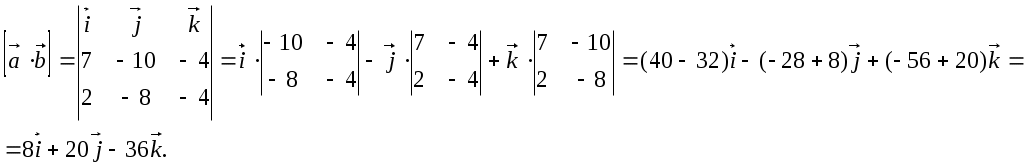 6. Найдём векторное произведениес d ;
6. Найдём векторное произведениес d ;
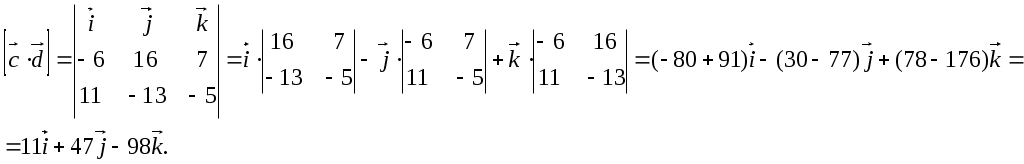 7. Найдём смешанное произведение (a с ) .d .
7. Найдём смешанное произведение (a с ) .d .
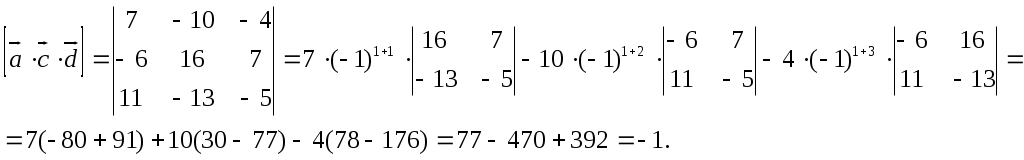
Задание 2.40
Написать уравнение прямой, проходящей через точки А и В в виде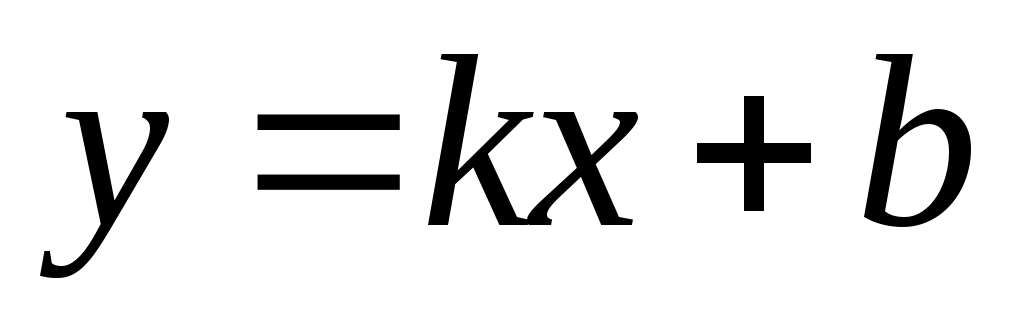 , построить эту прямую:
, построить эту прямую: 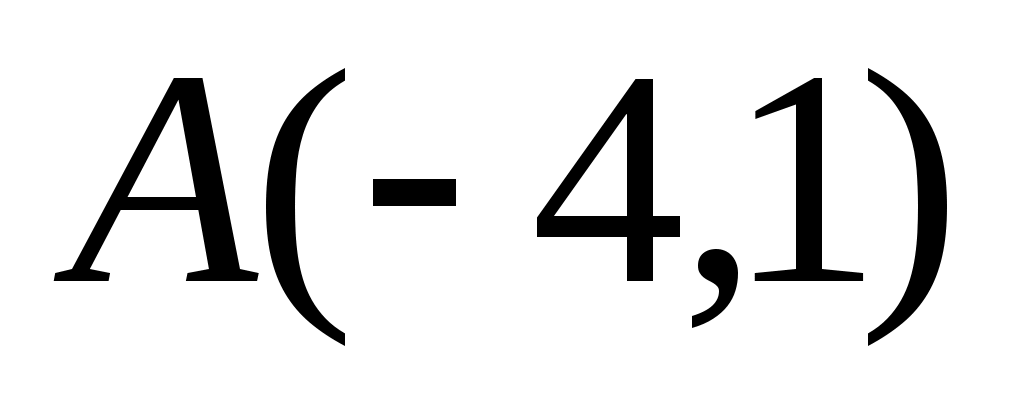 ,
, 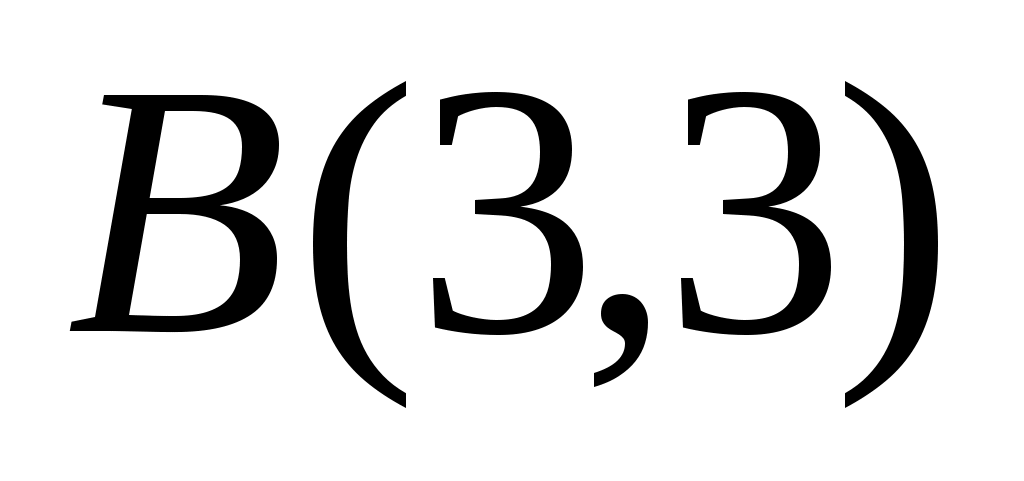 .
.
Решение
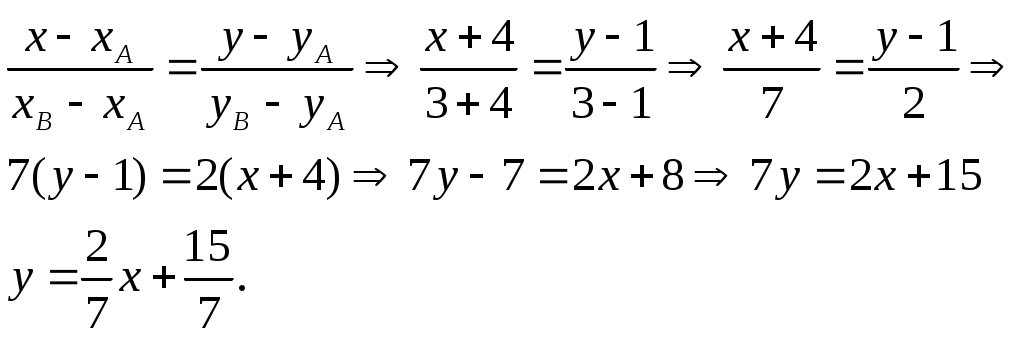 .
.
Сделаем рисунок.
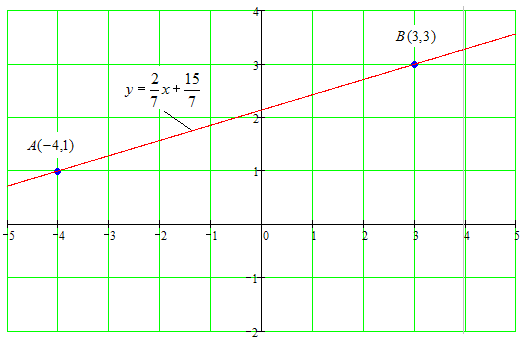
Задание 2.50
Даны вершины треугольника ABC.
A(-3, 0); B(-5, 2); C(3, 8).
Найти:
1) длину стороны AB;
2) уравнения стороны AB;
3) длину медианы AM;
4) уравнение медианы AM;
5) уравнение высоты BH;
6) длину высоты BH;
7) площадь треугольника;
8) угол BAC (в градусах);
9) уравнения прямой параллельной стороне ВС и проходящей через точку А.
В ответах надо приводить уравнения прямых в виде y = kx+b. Все вычисления проводить с двумя знаками после запятой.
Решение
1.Длину стороны АВ найдём по формуле расстояния между двумя точками: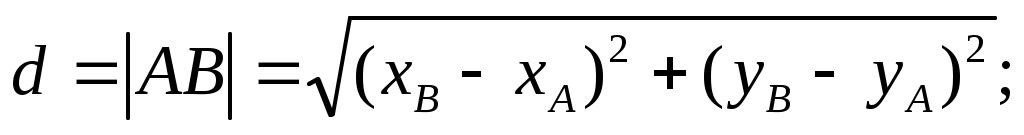
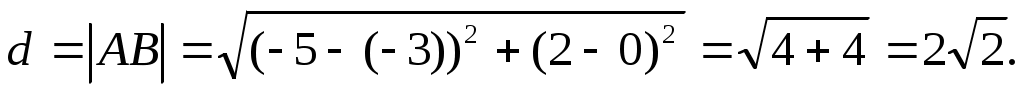
2.Уравнение стороны АВ запишем как уравнение прямой, проходящей через две заданные точки:
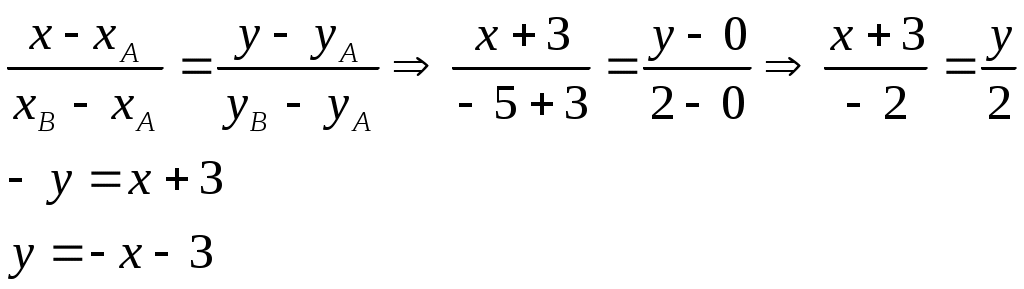
3.Найдём длину медианы АМ, но предварительно найдём координаты точки М. Так как медиана делит сторону, на которую она опущена пополам, то используя координаты деления отрезка пополам, запишем:
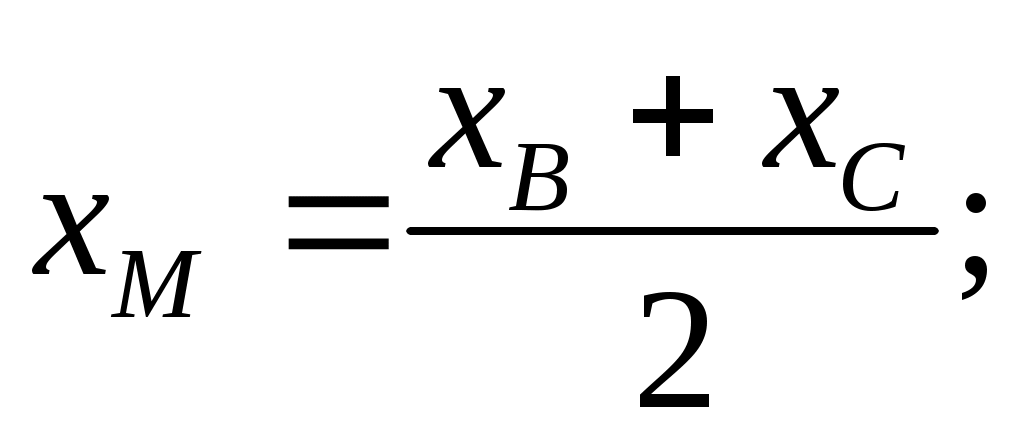
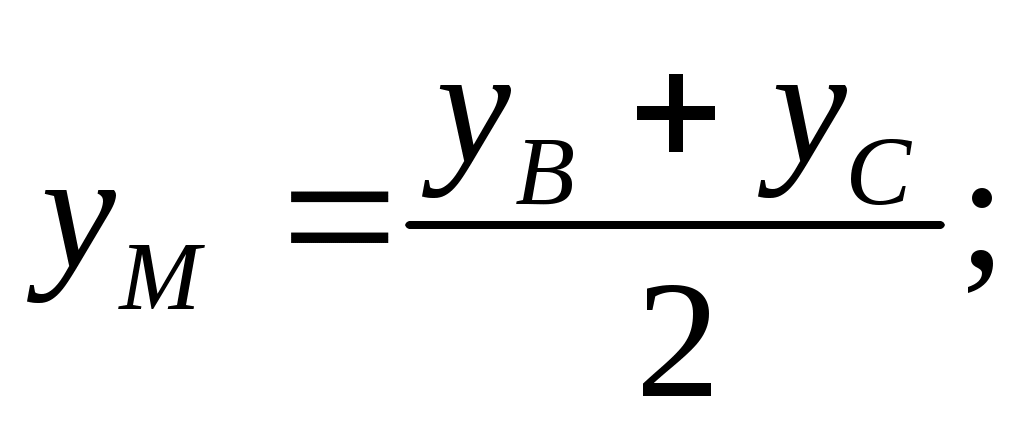
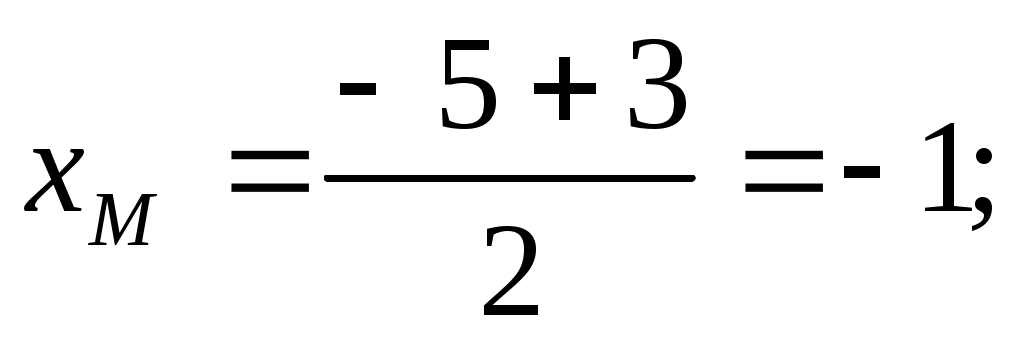
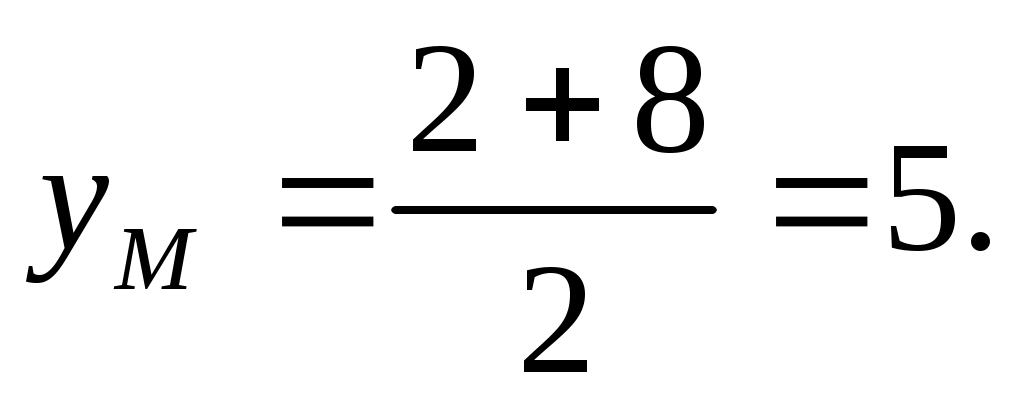
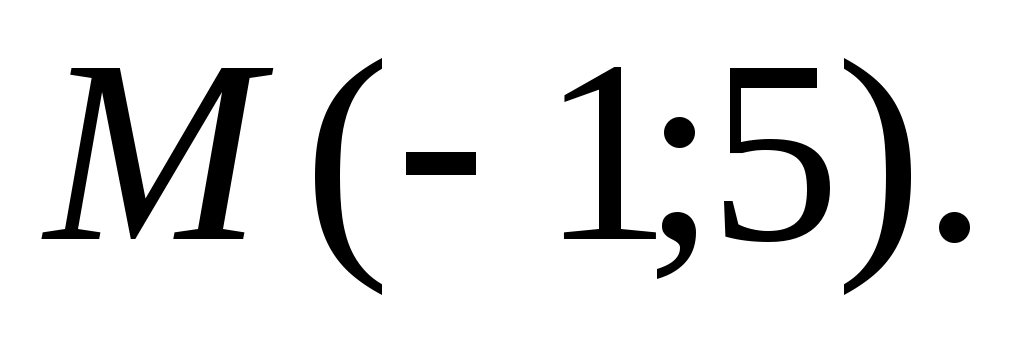
Тогда, найдём длину медианы:
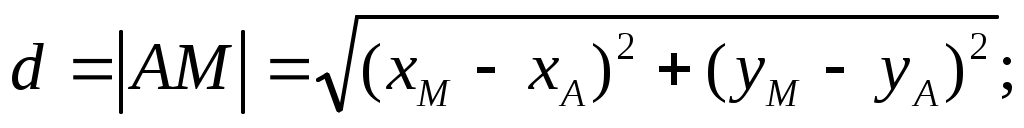
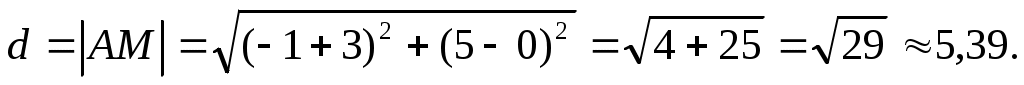
е) составить квадратное уравнение с действительными коэффициентами, корнем которого является
Решение
а) Умножим числитель и знаменатель на сопряжённый знаменателю множитель
алгебраическая форма комплексного числа.
Окончательно, получим тригонометрическую формулу данного числа:
Показательная форма комплексного числа:
б) Изобразим это число на комплексной плоскости:

в) Применим формулу:
Мы нашли тригонометрическую форму заданного числа
г) Найдём корни уравнения
Для извлечения корня применим формулу:
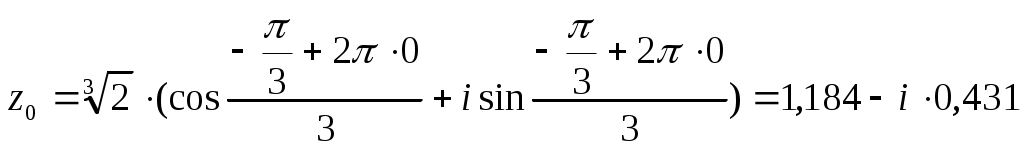 ,
,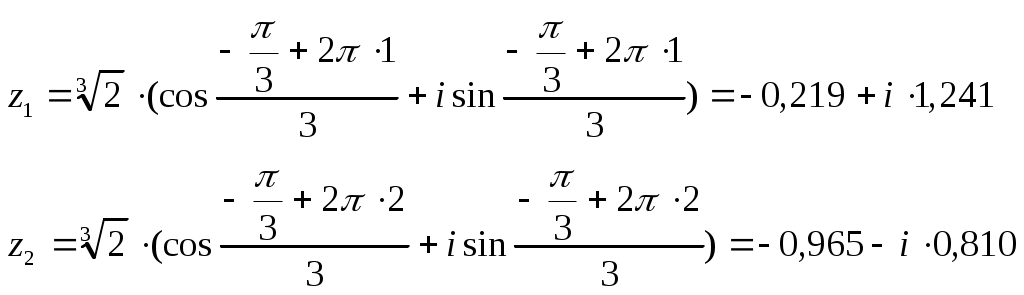
д) Вычислим произведение полученных корней.
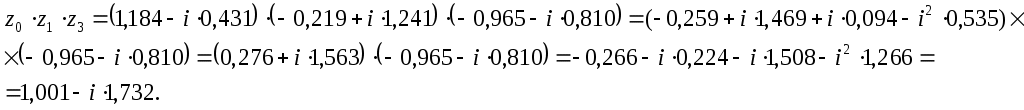
е) Составим квадратное уравнение с действительными коэффициентами, корнем которого является
Квадратное уравнение имеет вид:
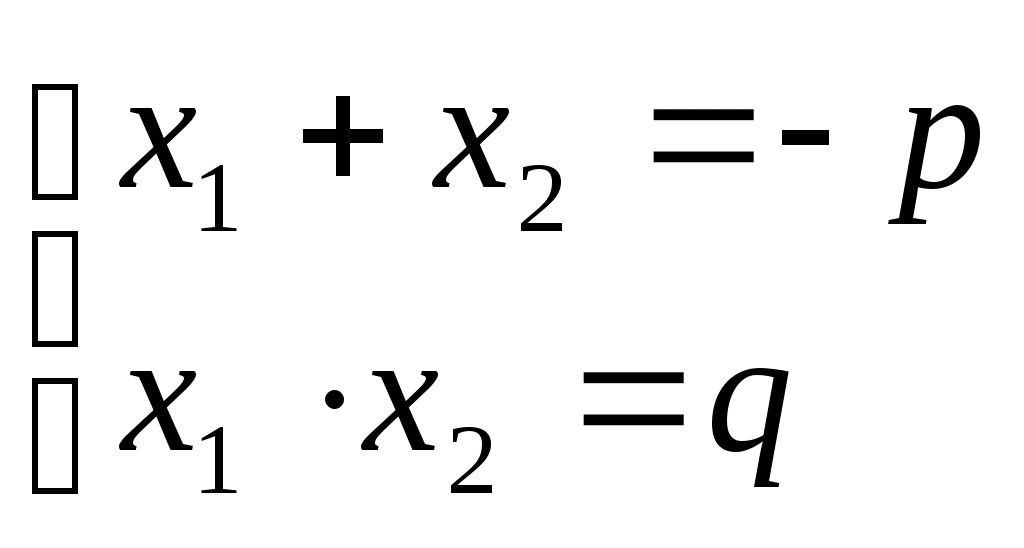
Один из корней
Тогда, квадратное уравнение примет вид:
Контрольная работа 2
Задание 2.10
Найти длину вектора
Решение
Найдём длину вектора:
Найдём скалярное произведение:
Задание 2.20
Написать уравнение плоскости, проходящей через точки M, K и L в виде
Решение
Уравнение плоскости ищем в виде:
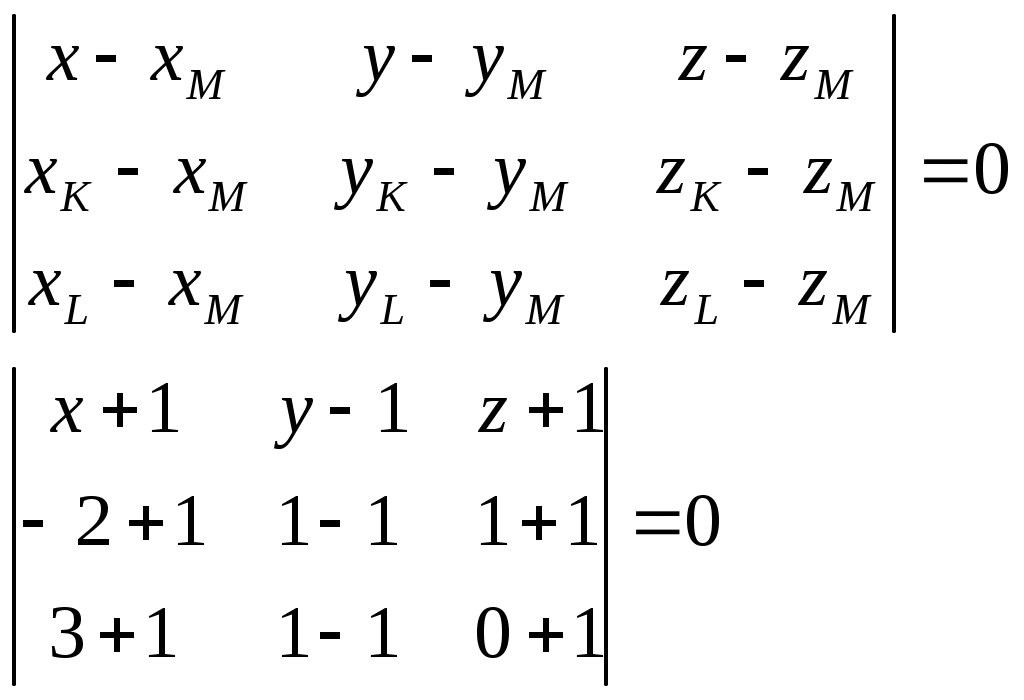
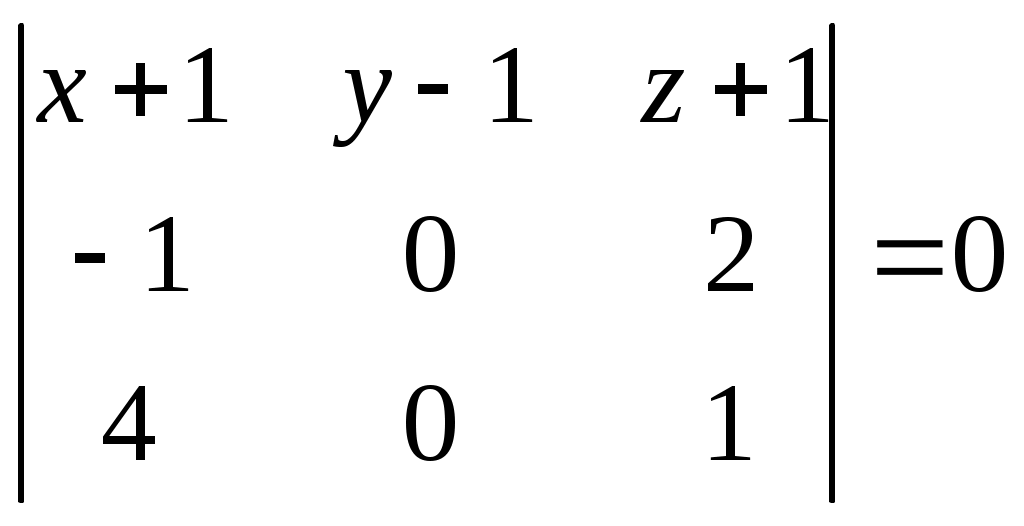
Раскроем определитель по элементам второго столбца:
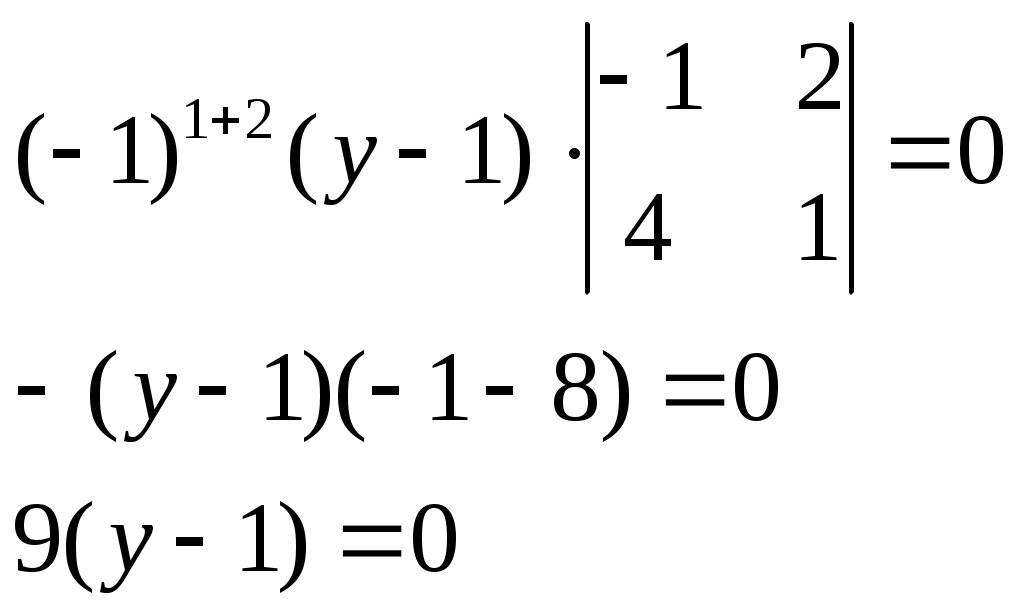
Следовательно, уравнение плоскости:
Задание 2.30
Даны 4 вектораa,b,c,d.
a(7, -10, -4); b(2, -8, -4); c(-6, 16, 7); d(11, -13, -5);
Вычислить:
1) координаты вектораd в базисе a,b,c;
2) a .b ;
3) с .d ;
4) (2a + 3b ) . (5c – 4d);
5) a b ;
6) с d ;
7) (a с ) .d .
Решение
1. Разложение вектора
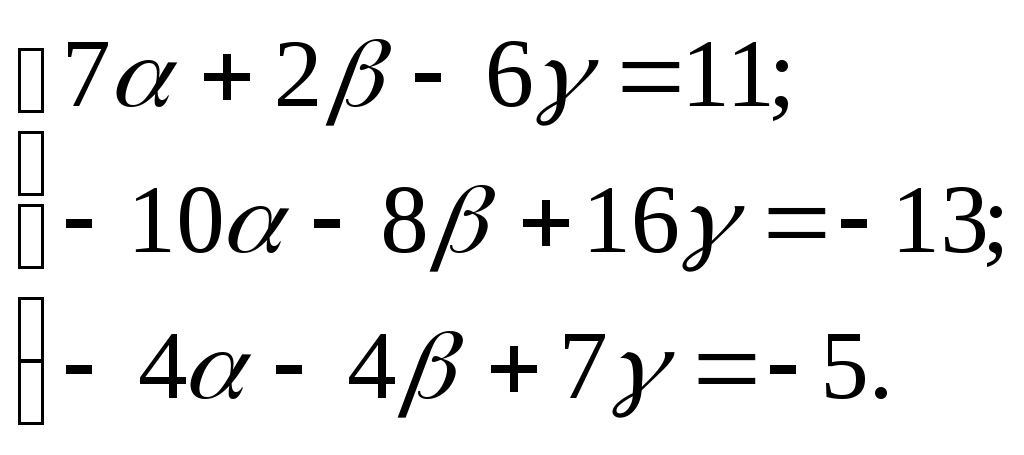
Найдём главный определитель системы:
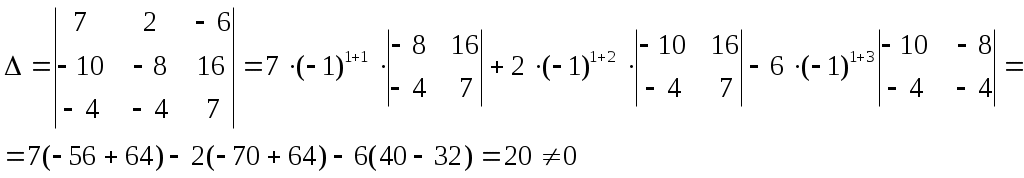
Так как определитель отличен от нуля, то векторы некомпланарные, линейно независимые, а значит, образуют базис. Значит, данная система имеет единственное решение, которое мы найдём по формулам Крамера:
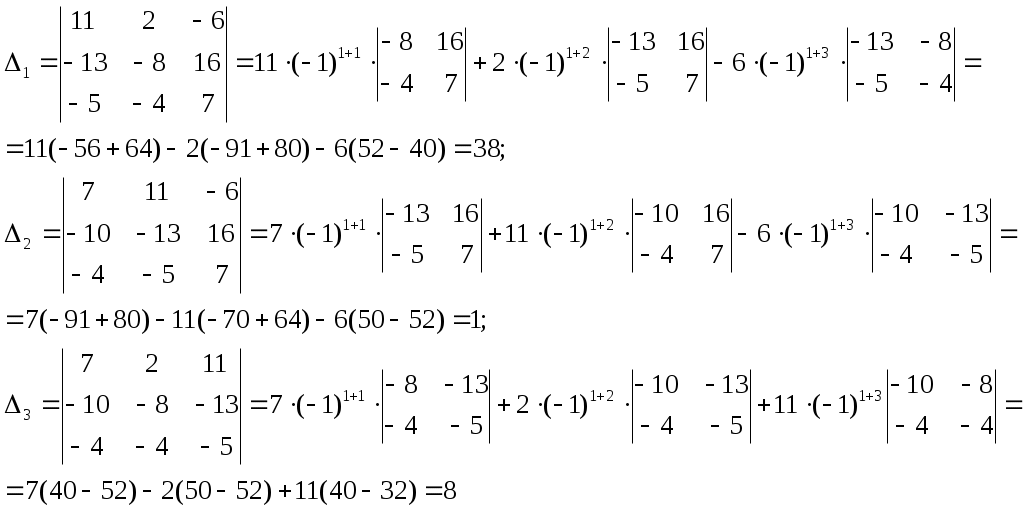
,
Таким образом,
2. Найдём скалярное произведение двух векторов:
3. Найдём скалярное произведение двух векторов:
4.
Найдём скалярное произведение:
5. Найдём векторное произведениеa b;
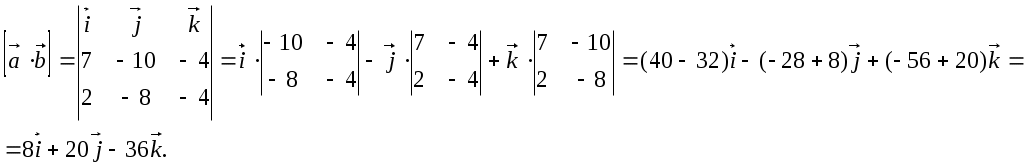 6. Найдём векторное произведениес d ;
6. Найдём векторное произведениес d ;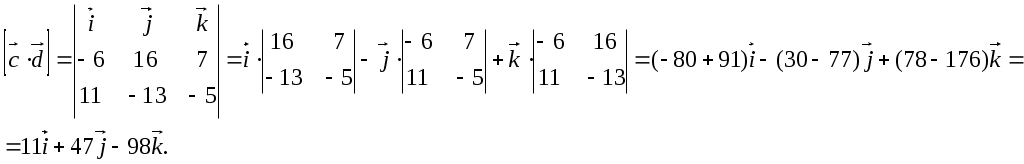 7. Найдём смешанное произведение (a с ) .d .
7. Найдём смешанное произведение (a с ) .d .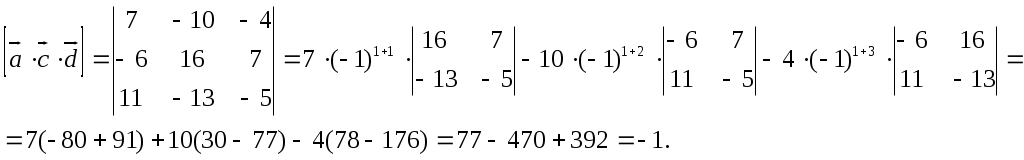
Задание 2.40
Написать уравнение прямой, проходящей через точки А и В в виде
Решение
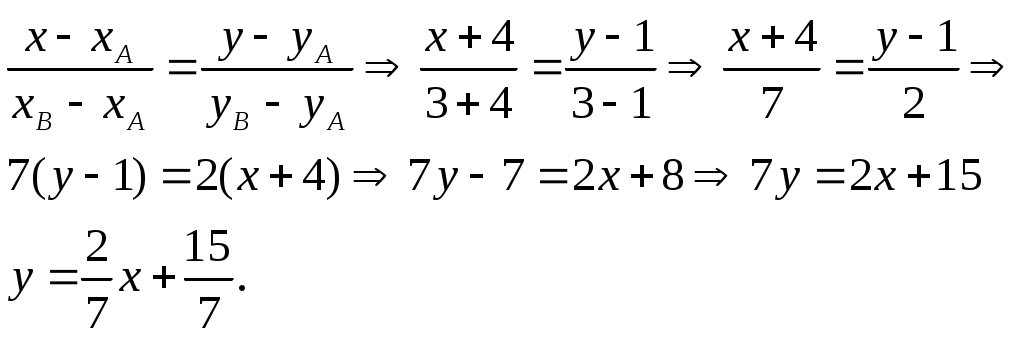 .
.Сделаем рисунок.

Задание 2.50
Даны вершины треугольника ABC.
A(-3, 0); B(-5, 2); C(3, 8).
Найти:
1) длину стороны AB;
2) уравнения стороны AB;
3) длину медианы AM;
4) уравнение медианы AM;
5) уравнение высоты BH;
6) длину высоты BH;
7) площадь треугольника;
8) угол BAC (в градусах);
9) уравнения прямой параллельной стороне ВС и проходящей через точку А.
В ответах надо приводить уравнения прямых в виде y = kx+b. Все вычисления проводить с двумя знаками после запятой.
Решение
1.Длину стороны АВ найдём по формуле расстояния между двумя точками:
2.Уравнение стороны АВ запишем как уравнение прямой, проходящей через две заданные точки:
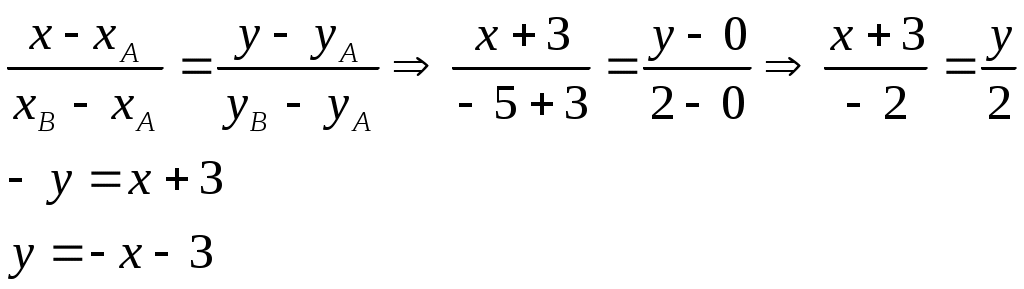
3.Найдём длину медианы АМ, но предварительно найдём координаты точки М. Так как медиана делит сторону, на которую она опущена пополам, то используя координаты деления отрезка пополам, запишем:
Тогда, найдём длину медианы: