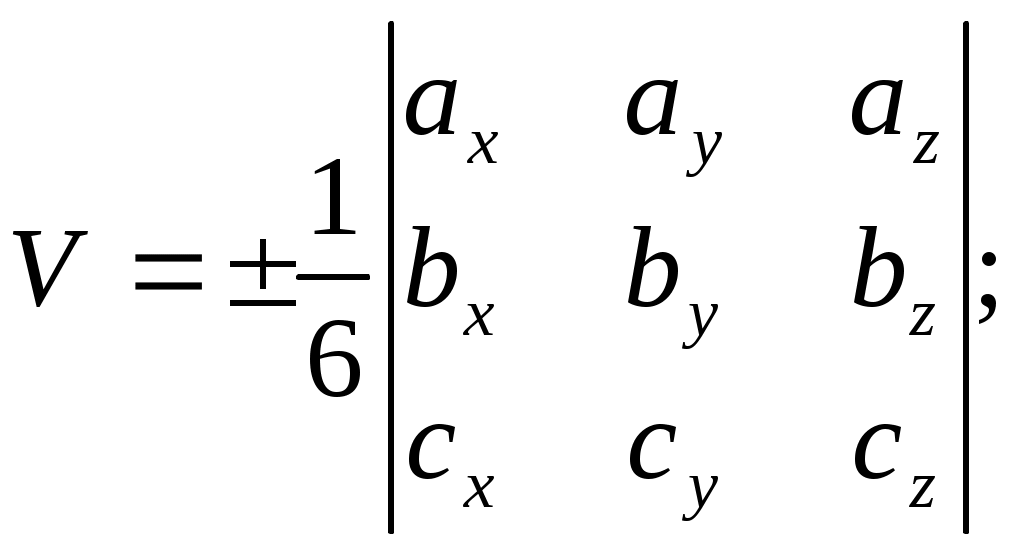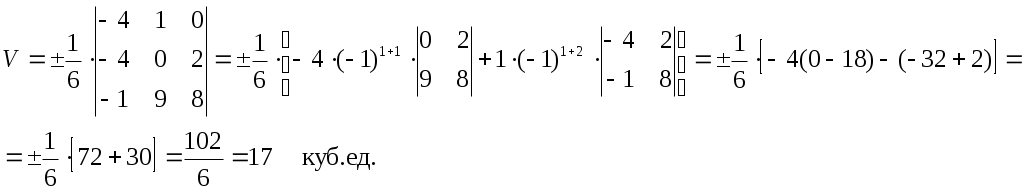4.Запишем уравнение медианы :




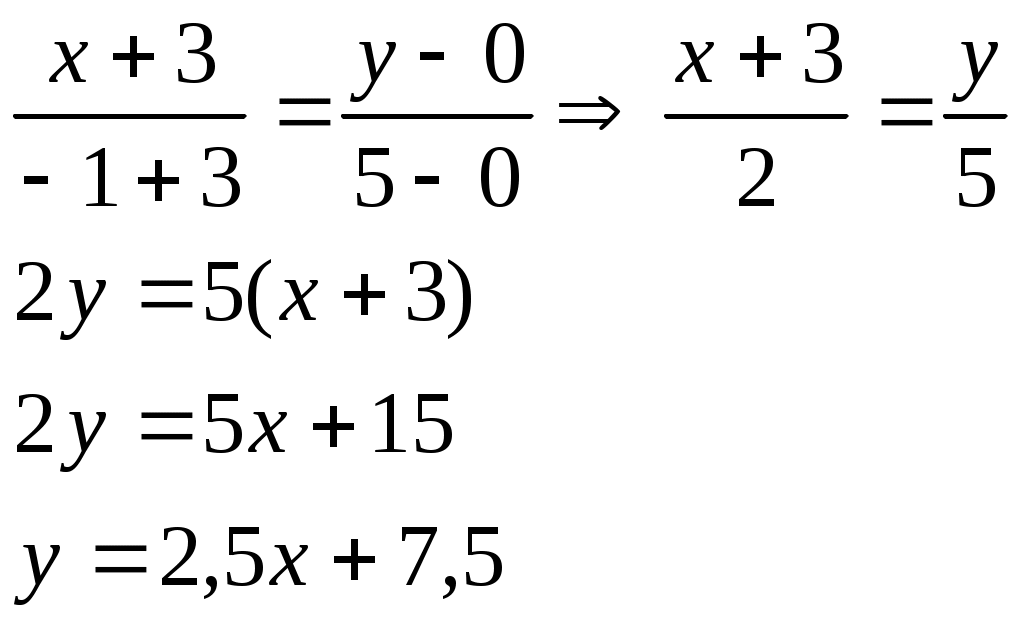
5.Высота опущена на сторону поэтому уравнение высоты ищем как уравнение прямой, которая проходит через точку В и перпендикулярна прямой АС. Тогда можем записать:



Найдём уравнение прямой АС:



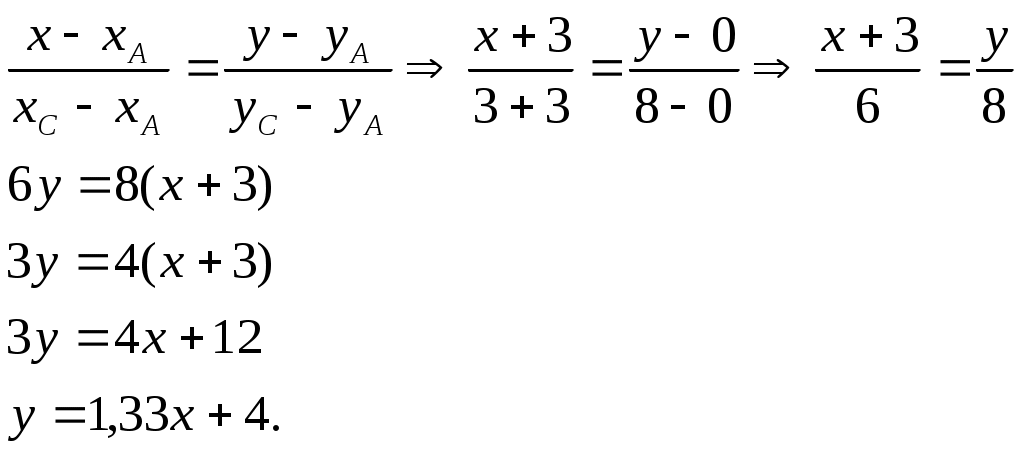
Для прямой АС угловой коэффициент равен , тогда используя условие перпендикулярности, угловой коэффициент для прямой равен: Окончательно, получим уравнение высоты


6.Найдём длину высоты



Координаты т. найдём как точку пересечения двух прямых, решив систему уравнений:









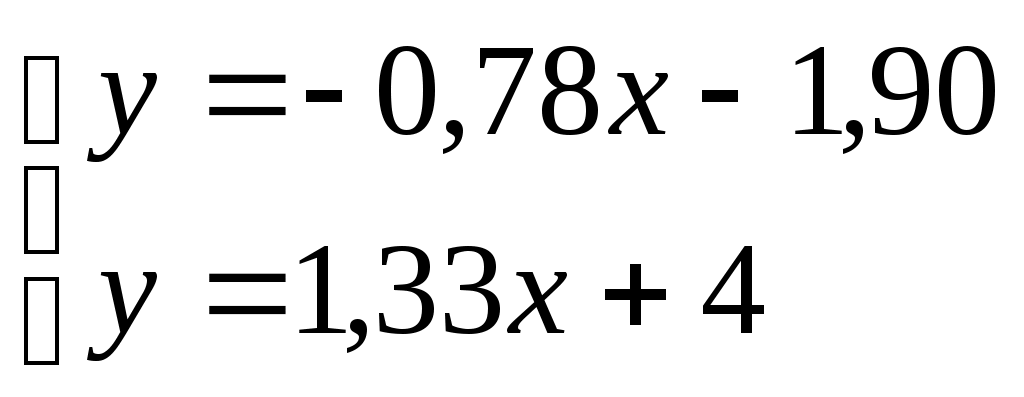
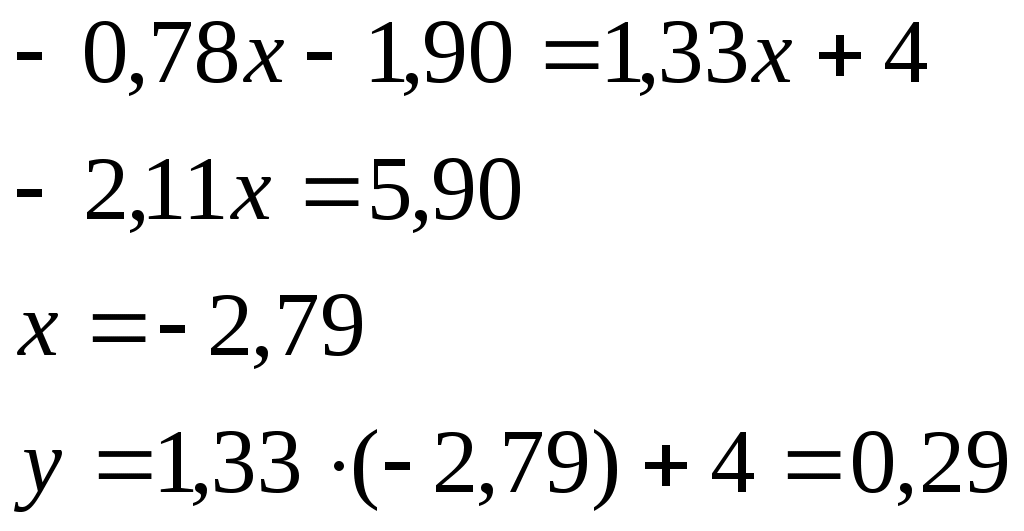
7. Площадь треугольника АВС найдём по следующей формуле:

---

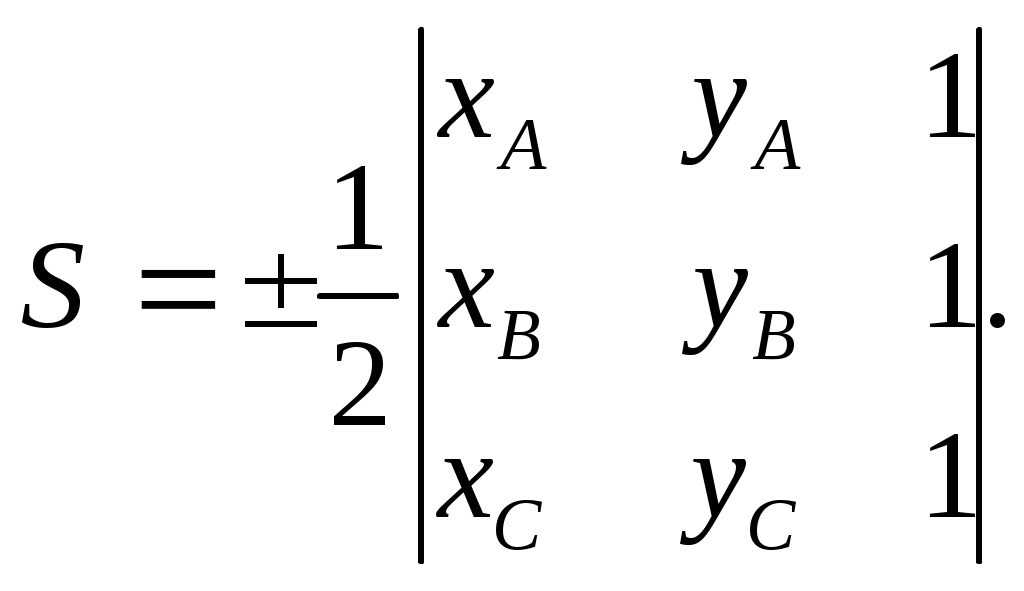
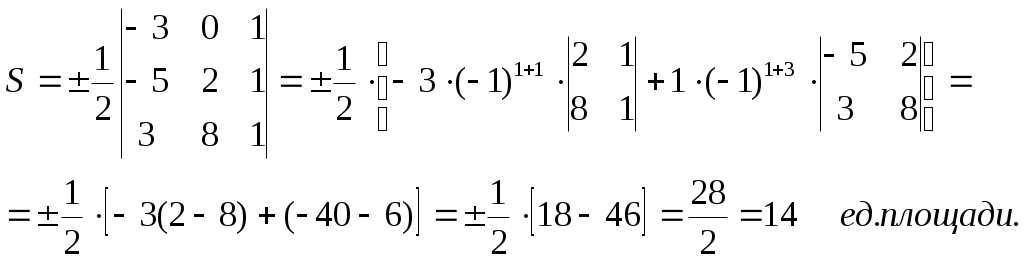
8.Угол ВАС найдём по следующей формуле:

Угол ВАС – это угол между двумя прямыми АВ и АС, угловой коэффициент для прямой АВ:


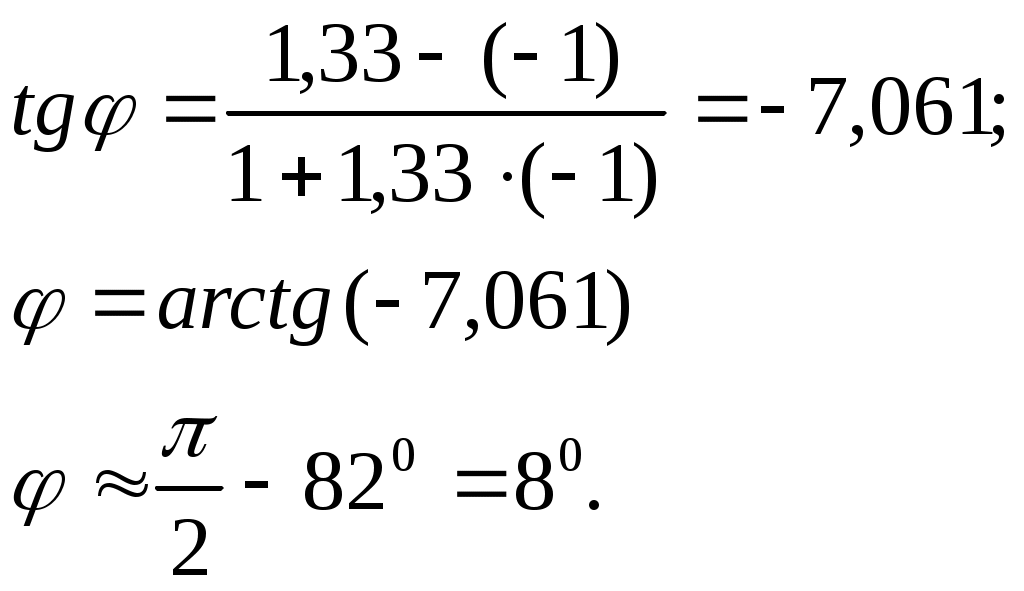
9.Запишем уравнение стороны ВС:

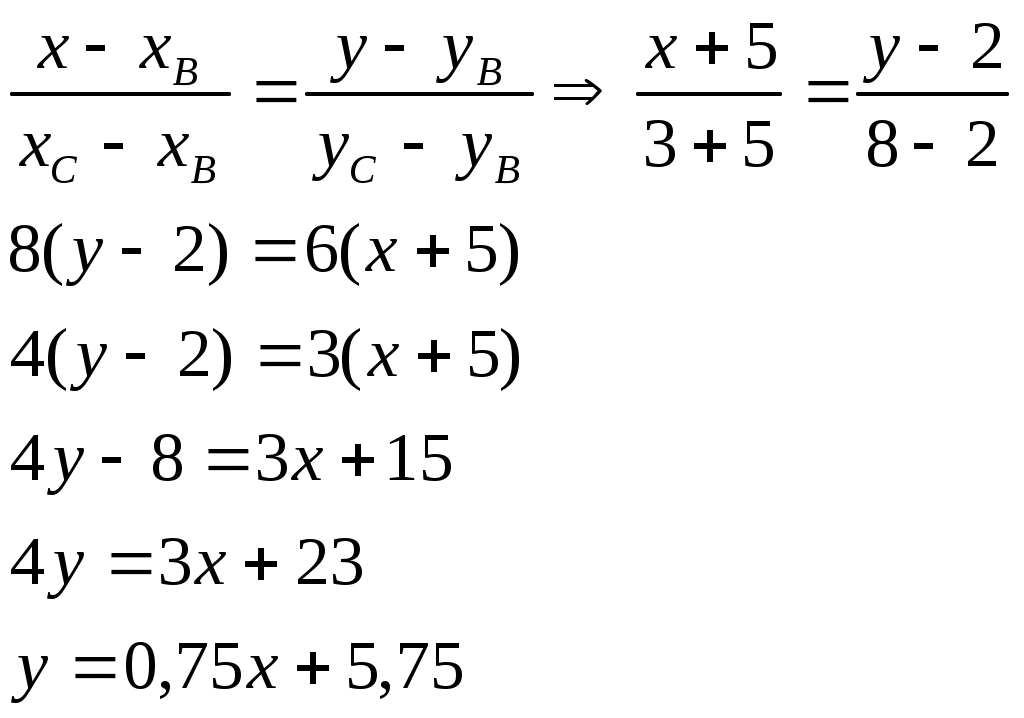
Угловой коэффициент для прямой ВС: . Он будет таким же и для искомой прямой, так как они параллельны, тогда запишем уравнение будущей прямой в виде:

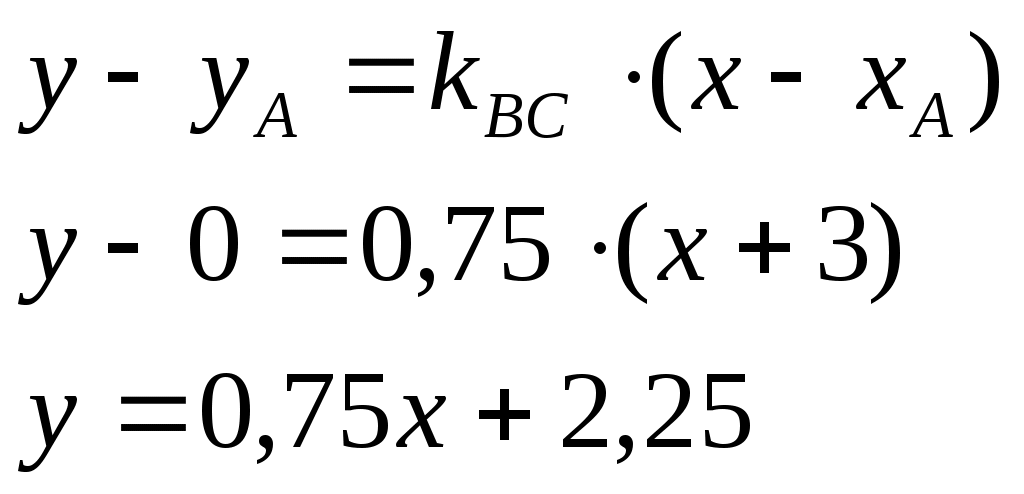
Сделаем рисунок.



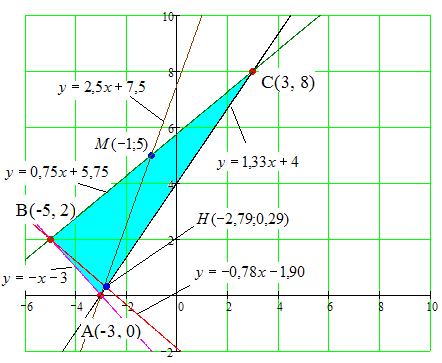
Задание 2.60
Написать уравнение плоскости в виде , проходящей через точку М параллельно векторам и .



Решение



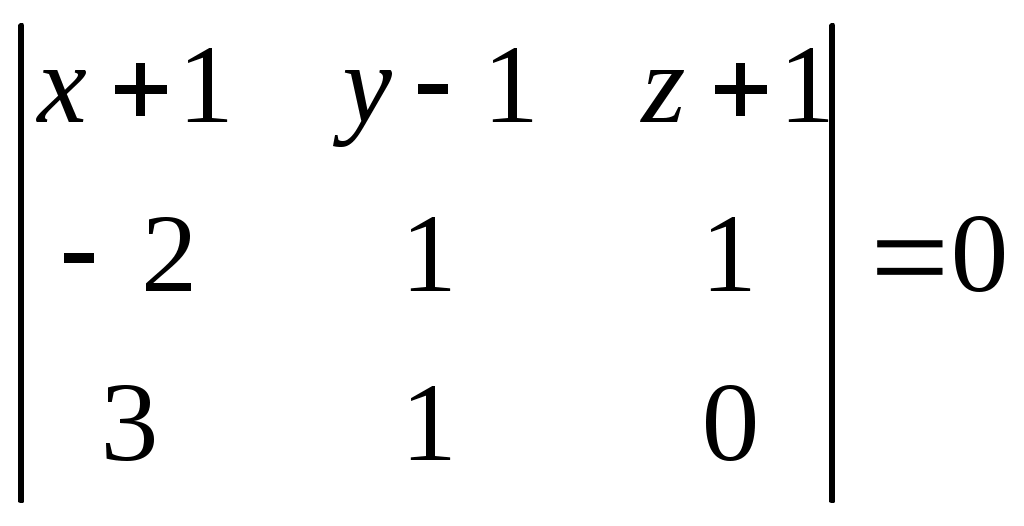
Раскрываем определитель по элементам первой строки:



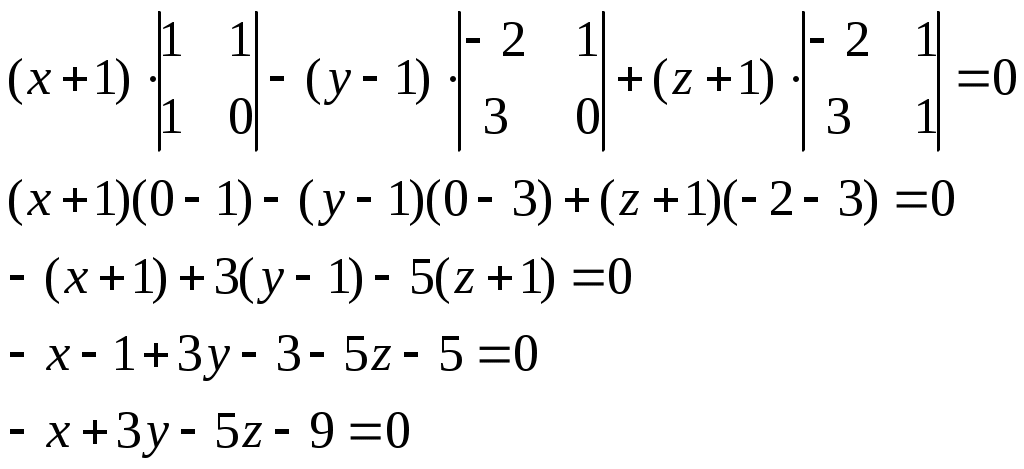
Следовательно, уравнение плоскости: .

Задание 2.70

Даны вершины пирамиды SPMN.

S(4, 0, 0); P(0, 1, 0); M(0, 0, 2); N(3,9,8).

Найти:

1) длину ребра SN;

2) уравнение ребра SN;

3) уравнение грани SPN;

4) площадь грани SPN;

5) уравнение высоты, опущенной из вершины S на грань PMN;

6) длину высоты, опущенной из вершины S на грань PMN;

7) угол между ребрами SP и SN (в градусах);

8) угол между ребром SP и гранью PMN (в градусах);

9) объем пирамиды.

В ответах надо приводить уравнения плоскостей и прямых в виде

---

Аx+ Вy + Cz + D = 0 и . Все вычисления проводить с двумя знаками после запятой.

Решение

1.Длину ребра найдём по формуле расстояния между двумя точками:

2.Уравнеие ребра запишем в каноническом виде:



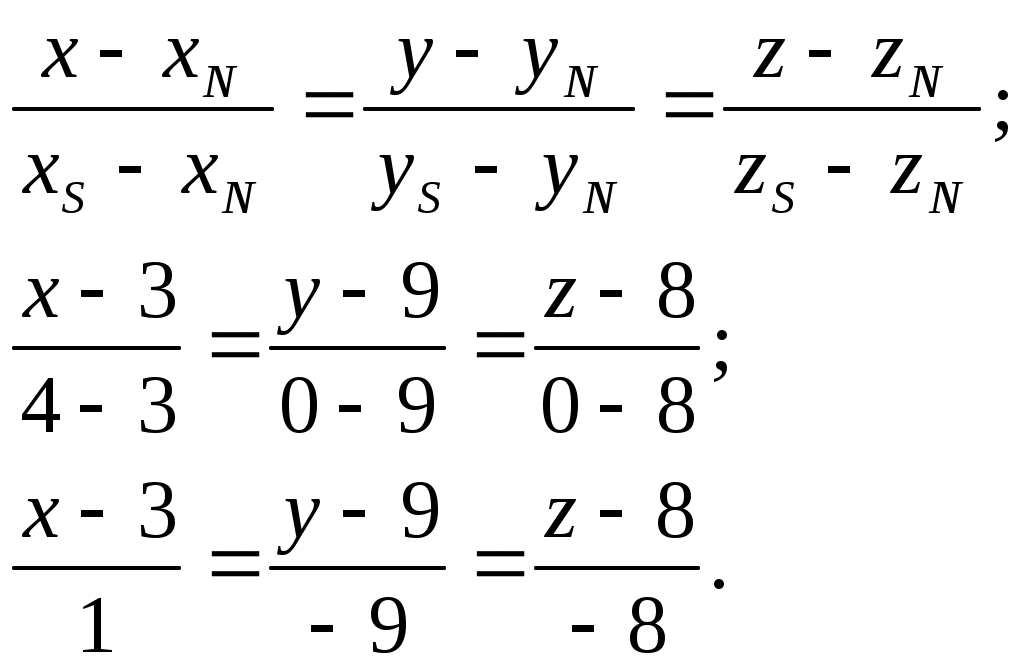
где направляющий вектор прямой.

3.Уравнение грани находим по следующей формуле:



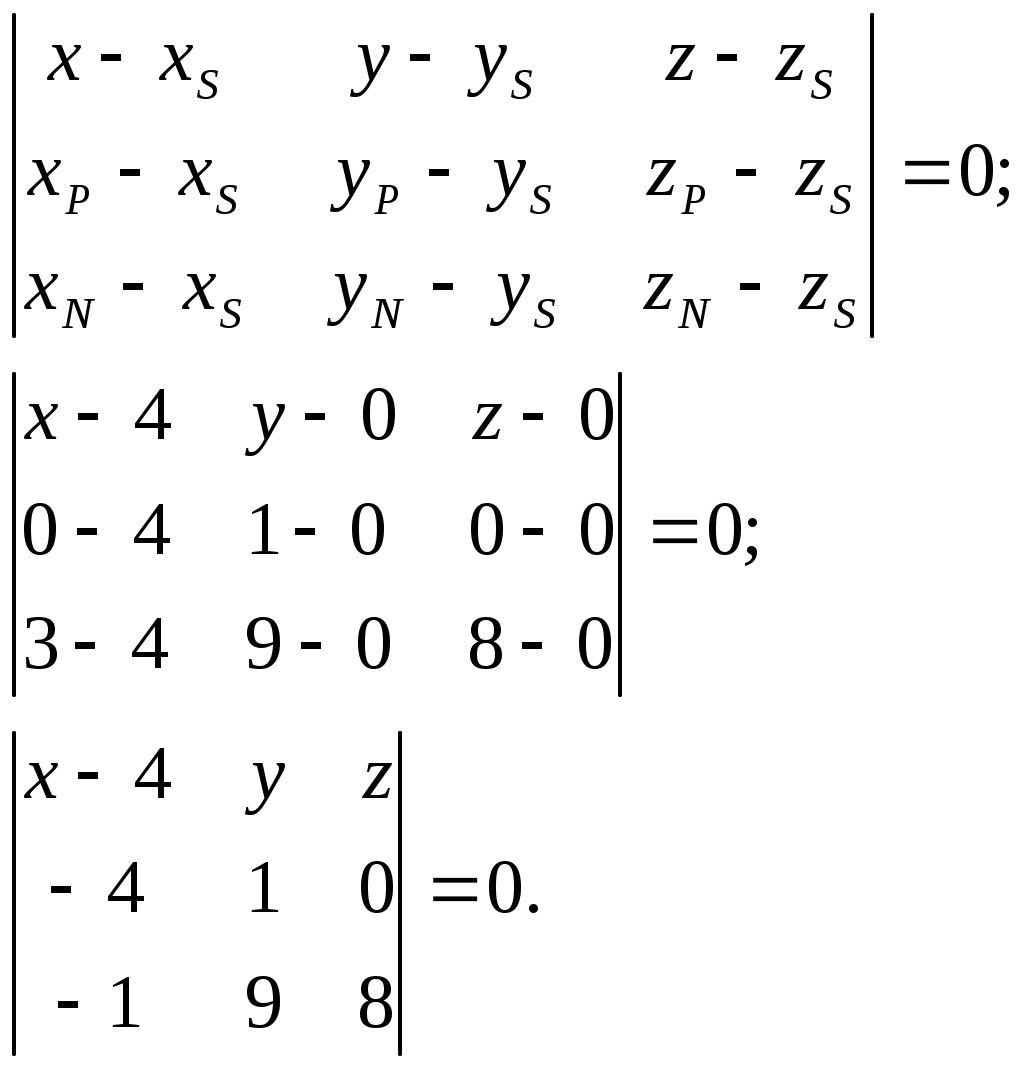
Разложим определитель по элементам первой строки:



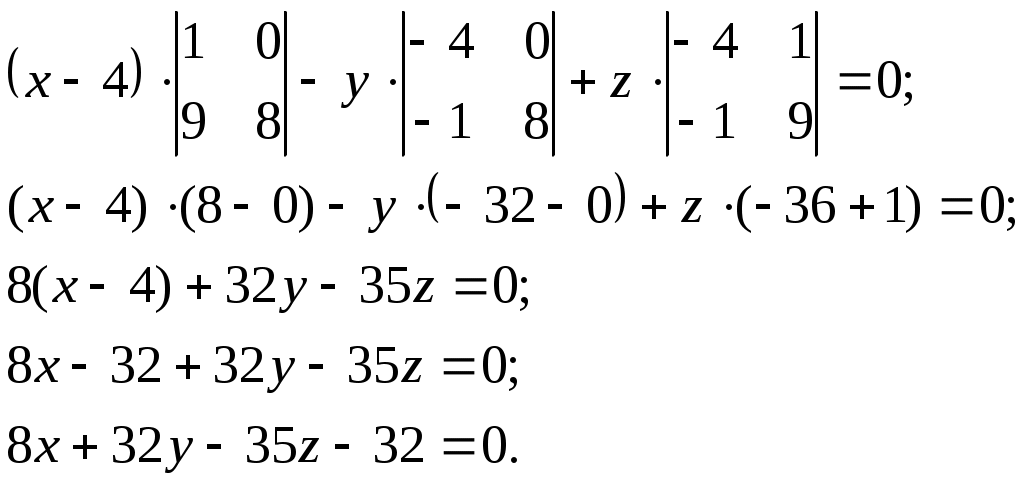
4.Найдём площадь грани .

Треугольник является половиной параллелограмма, построенного на векторах , тогда .











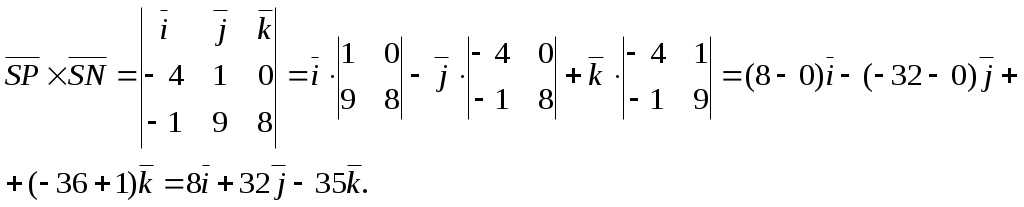
5.Найдём уравнение высоты, опущенной из вершины на грань

Если прямая проходит через точку S(4; 0; 0) и параллельна нормальному вектору

---

к грани , то ее уравнение определяется следующим выражением:



Нормальный вектор ищем из следующего выражения:



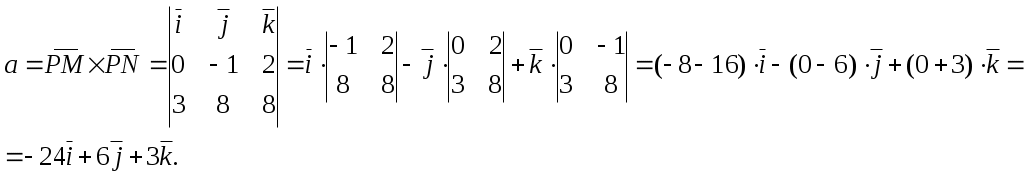
Тогда координаты нормального вектора плоскости : И уравнение высоты, опущенной из вершины S на грань примет окончательный вид:


6.Найдём длину высоты, опущенной из вершины на грань

Расстояние от точки до плоскости определяется выражением:



Но для начала найдём уравнение грани





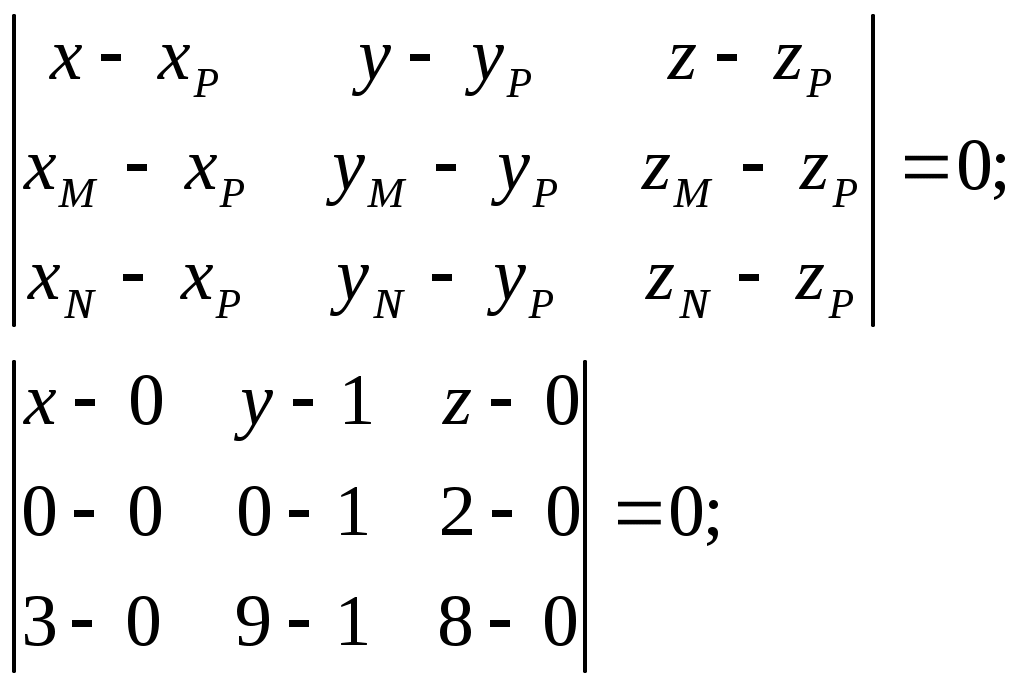
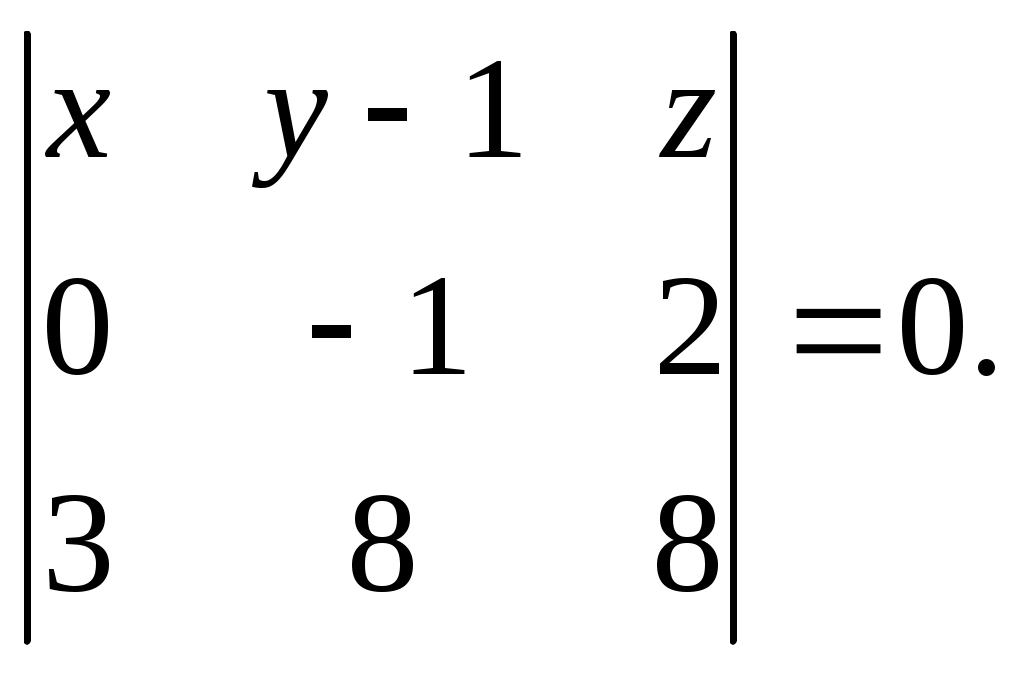
Разложим определитель по элементам первого столбца:



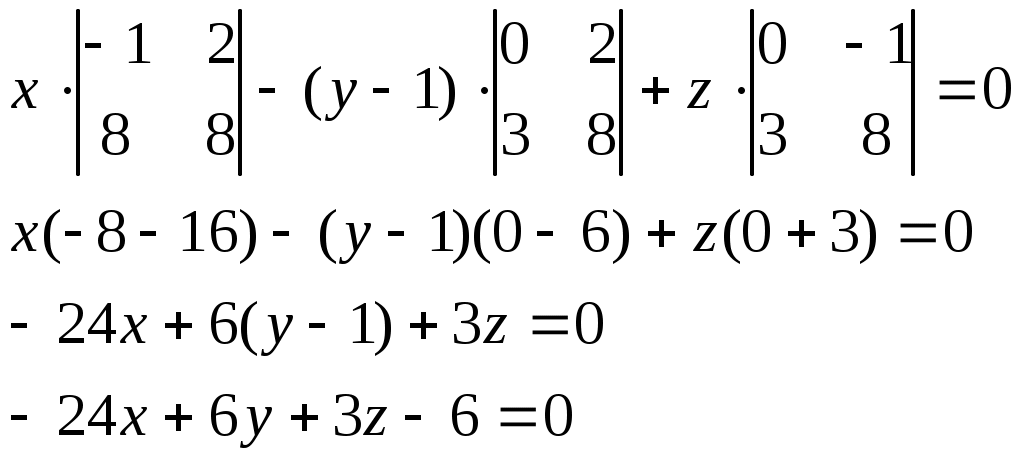
Или для нашего случая



7.Найдём угол между рёбрами и (в градусах);

Угол между рёбрами будем искать как угол между двумя направляющими векторами данных прямых. Для прямой

---

координаты направляющего вектора: а для прямой координаты направляющего вектора: . Тогда по формуле, находим



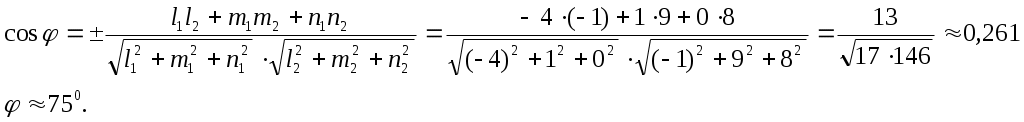
8.Найдём угол между ребром и гранью (в градусах);

Направляющий вектор прямой имеет координаты , а координаты нормального вектора плоскости следующие Тогда угол найдём по следующей формуле:





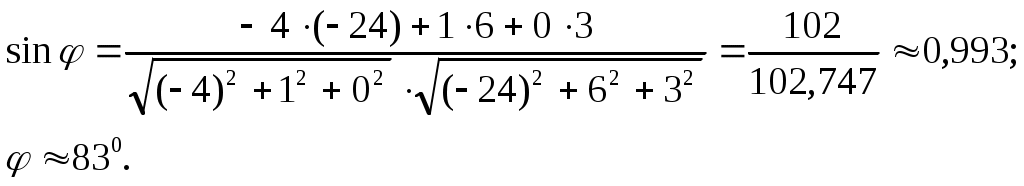
9.Найдём объём пирамиды, для этого рассмотрим векторы на которых построена данная пирамида:

Тогда,

---

Смотрите также файлы

• Тема История и генезис теории управления. Научная теория управления.pdf

• Программа среднего профессионального образования 44. 02. 03 Педагогика дополнительного образования (в области физкультурнооздоровительной деятельности) Дисциплина Родной язык Практическое занятие 2.docx

• Заполните таблицу Каждому из приведенных в ней терминов ниже положений, отмеченных цифрами, найдите соответствующее ему определение из таблицы 2.docx

• Организация Грант Выполнили Студентки группы 2 юр а.pptx

• Современные оздоровительные системы занятий физической культурой и спортом.docx