Файл: Контрольная работа 1 Задание 10 Вычислить определители а, б. Решение а. б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 100
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Используя матричные операции, выразить
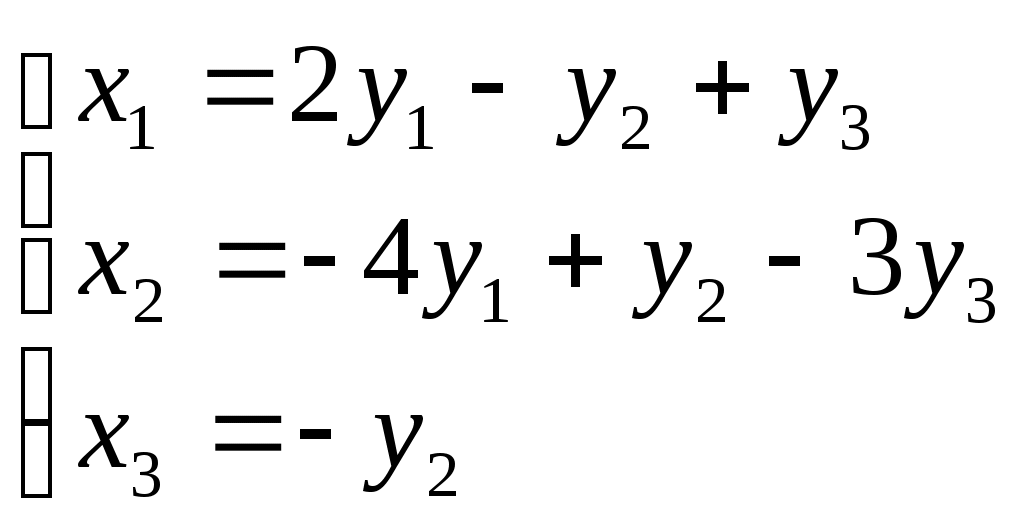
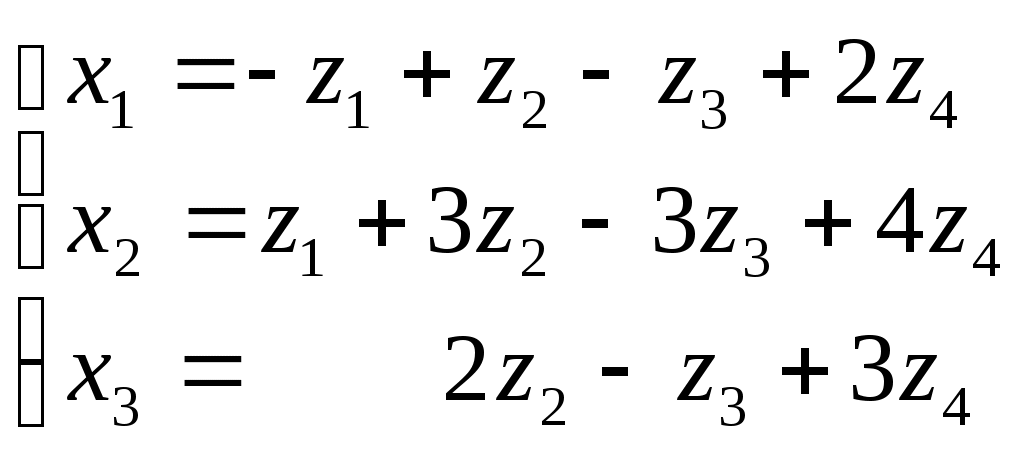
Решение
Пусть
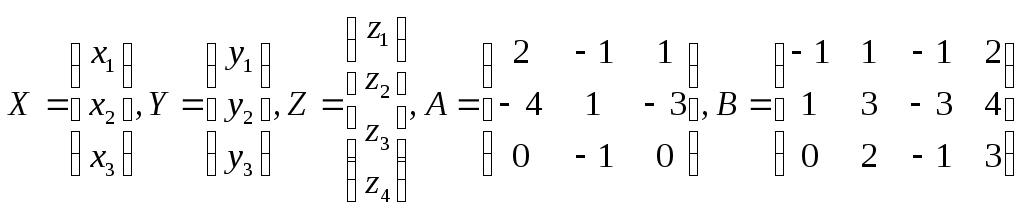 .
.Тогда заданные системы уравнений запишем в матричном виде:
Приравниваем правые части (2) и (1):
Найдём матрицу
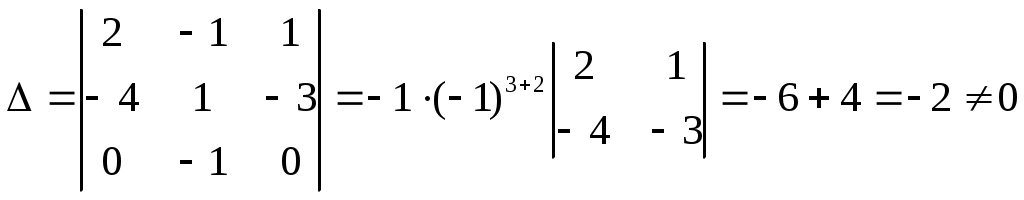 .
.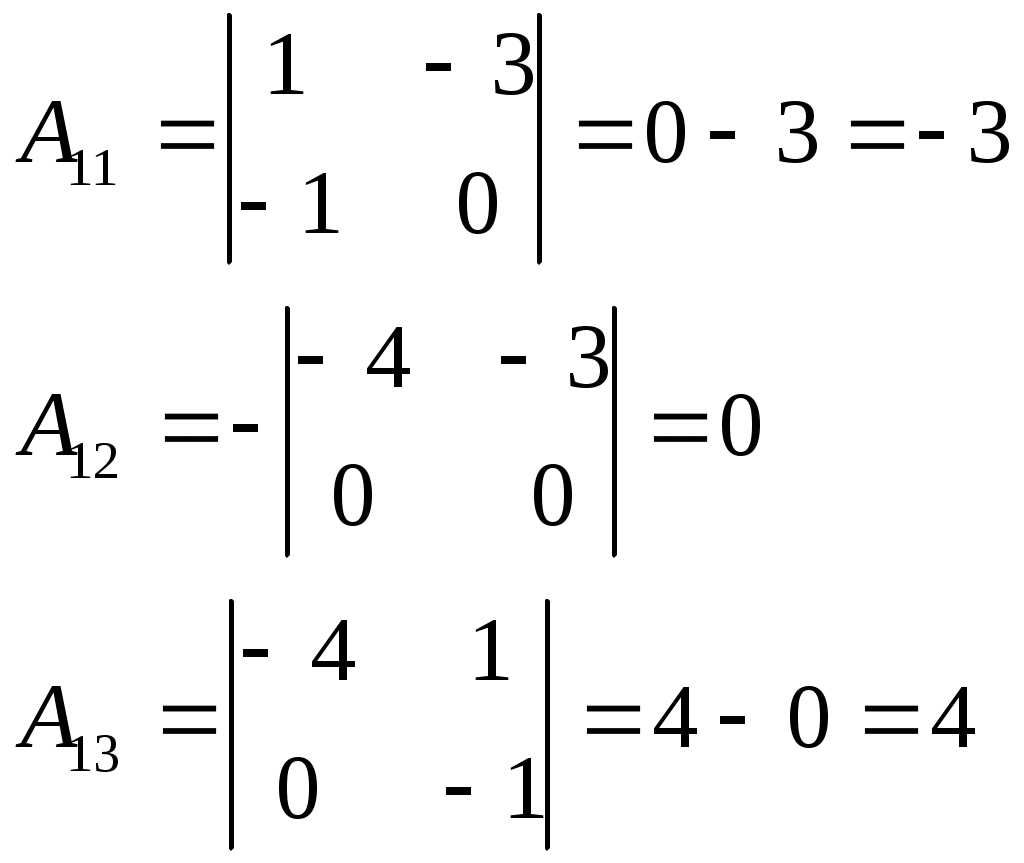
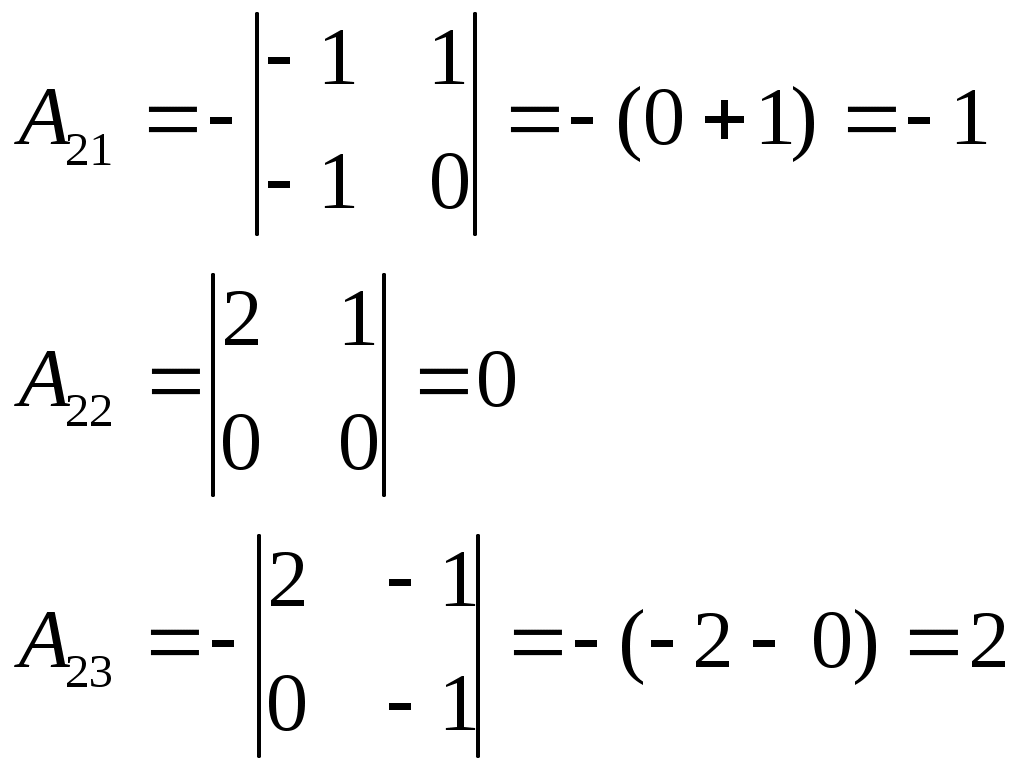
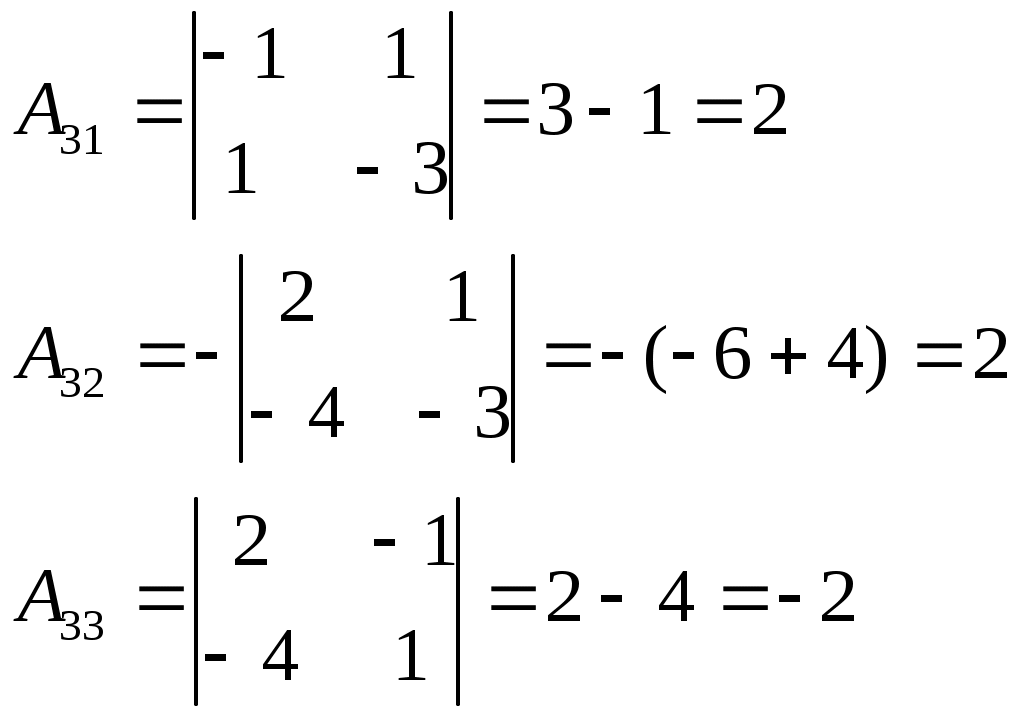
Тогда, запишем обратную матрицу:
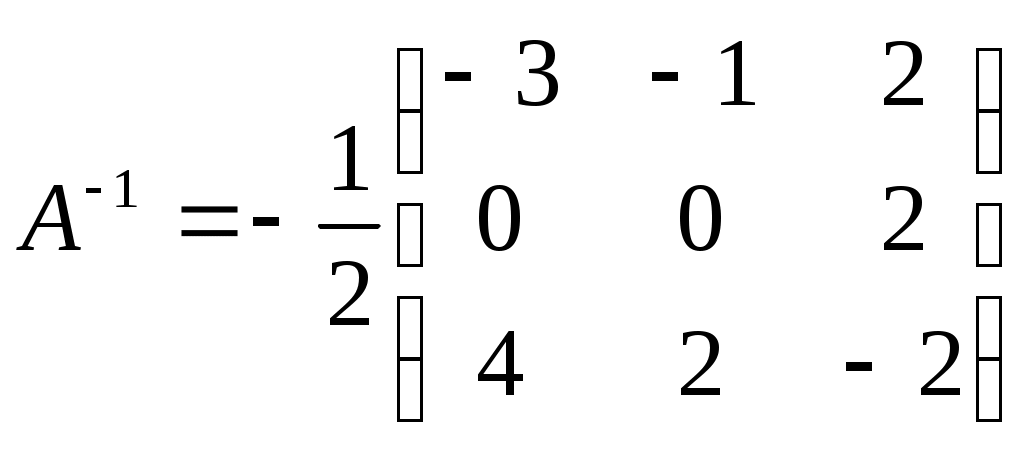 .
.Найдём произведение
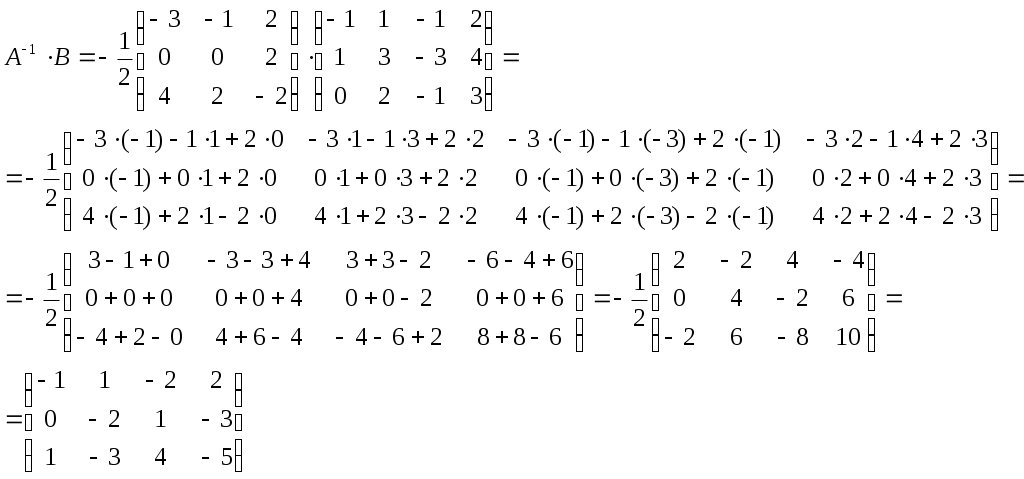
То есть, искомое выражение
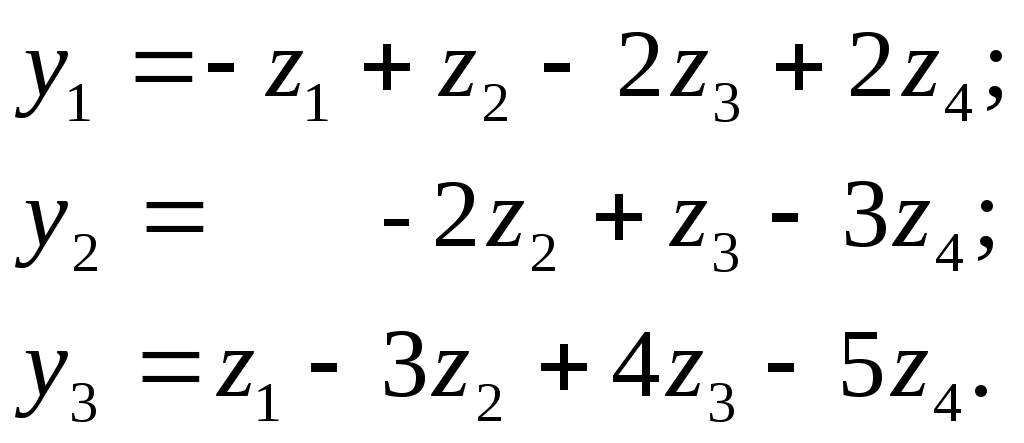
Задание 1.70
Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей А.
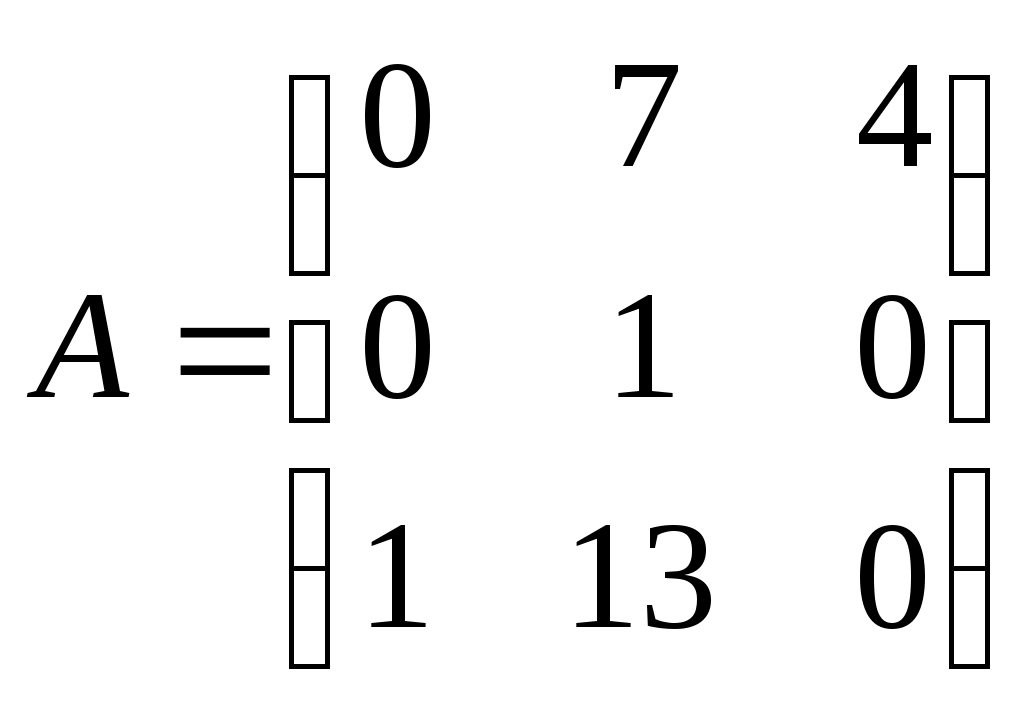
Решение
Характеристическое уравнение матрицы А примет вид:
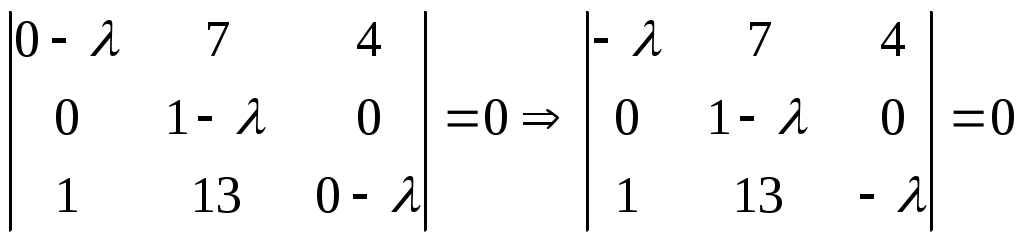
Раскрывая определитель по элементам второй строки, получим
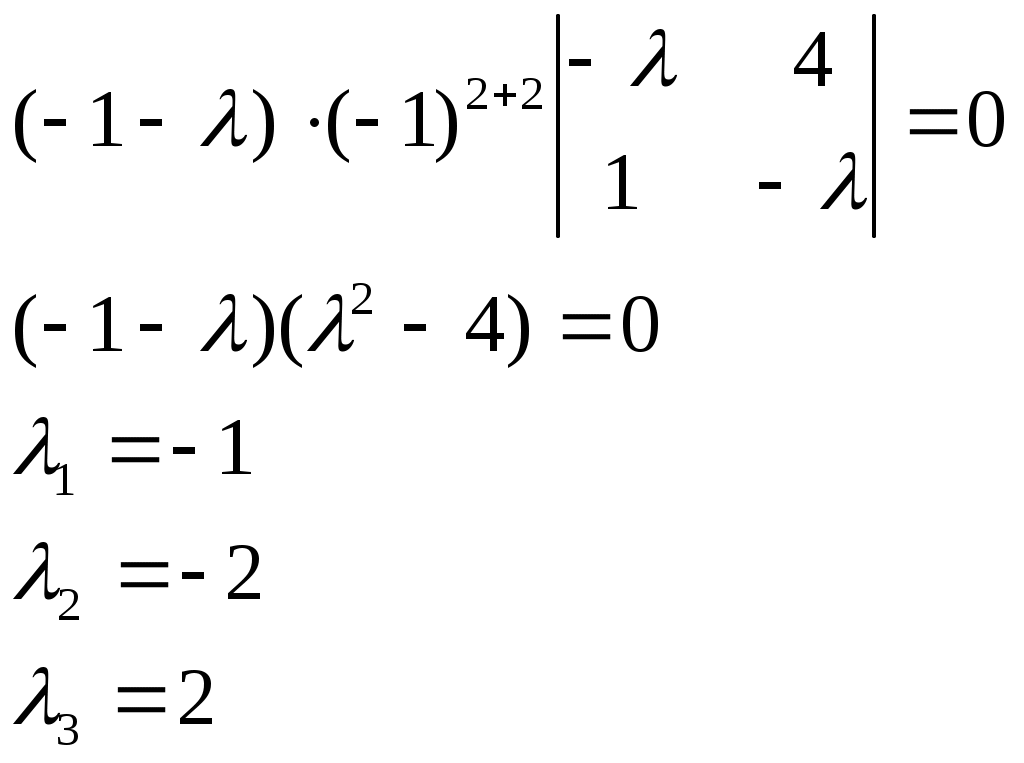
Получили три собственных значения. Определим координаты собственных векторов. При
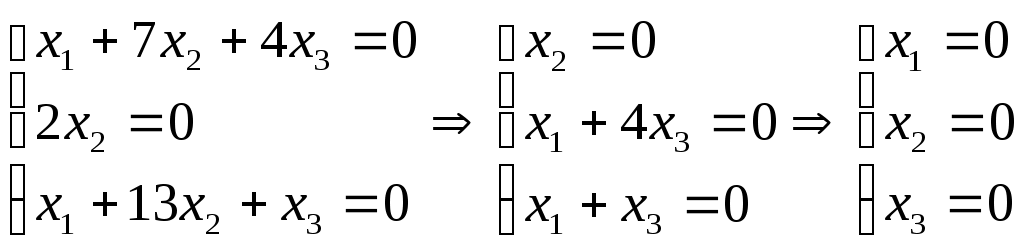 , собственный вектор нулевой:
, собственный вектор нулевой: 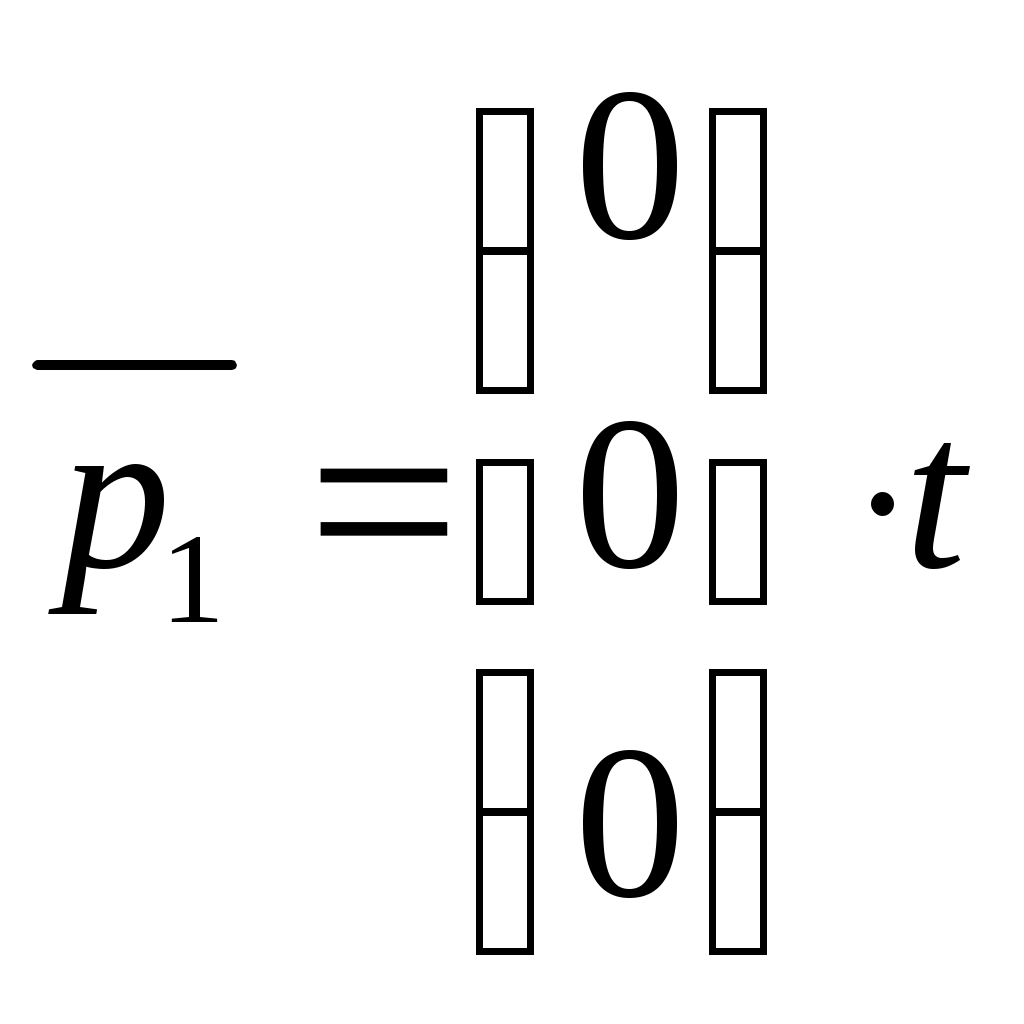 , где
, где При
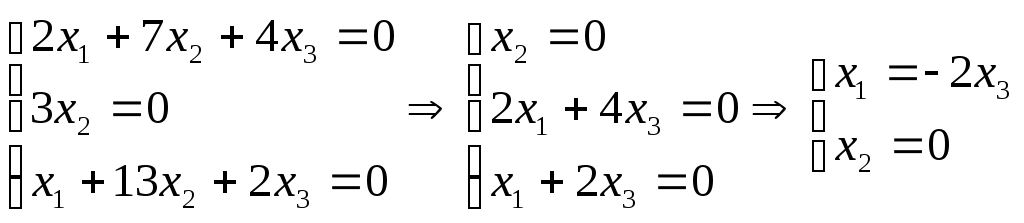 , пусть
, пусть Откуда,
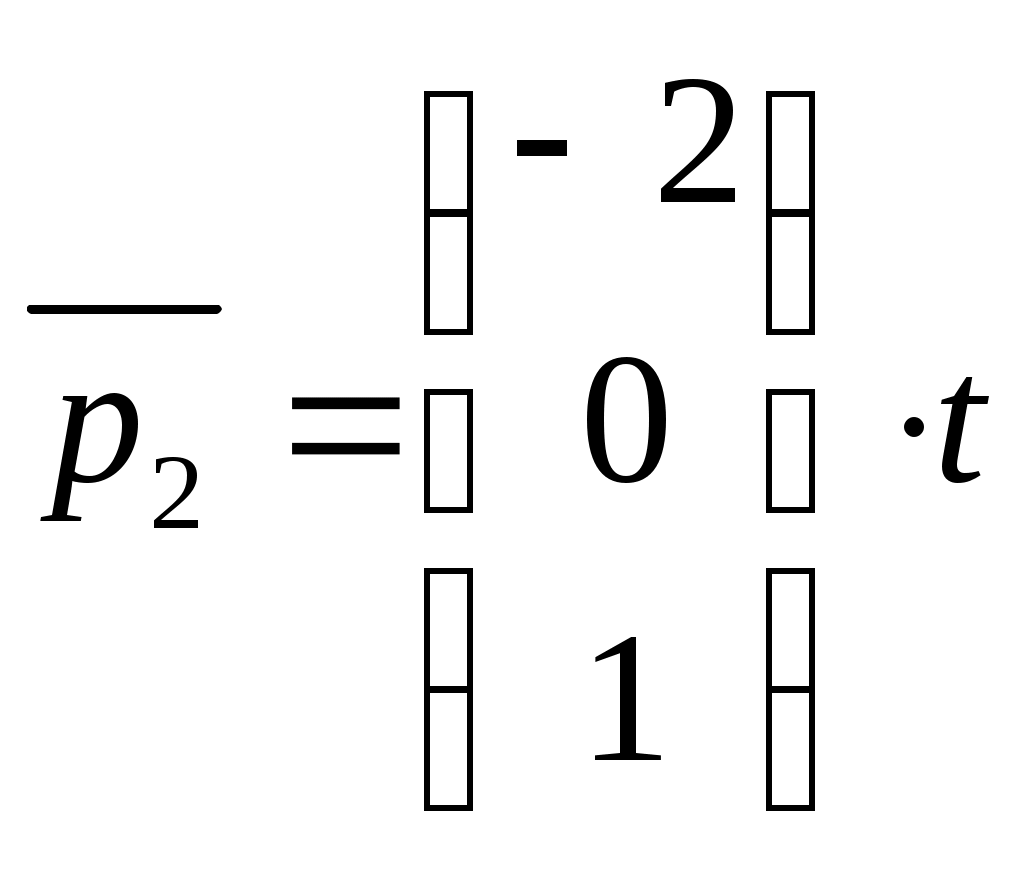 , где
, где При
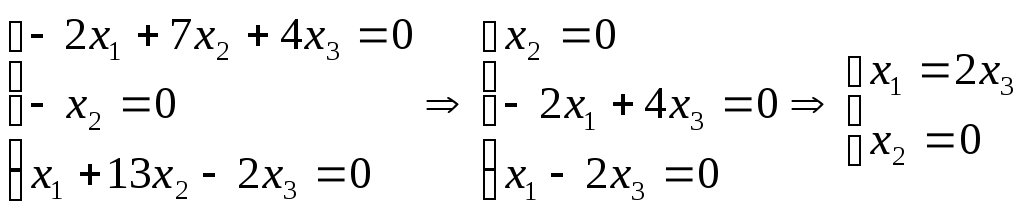 , пусть
, пусть Откуда,
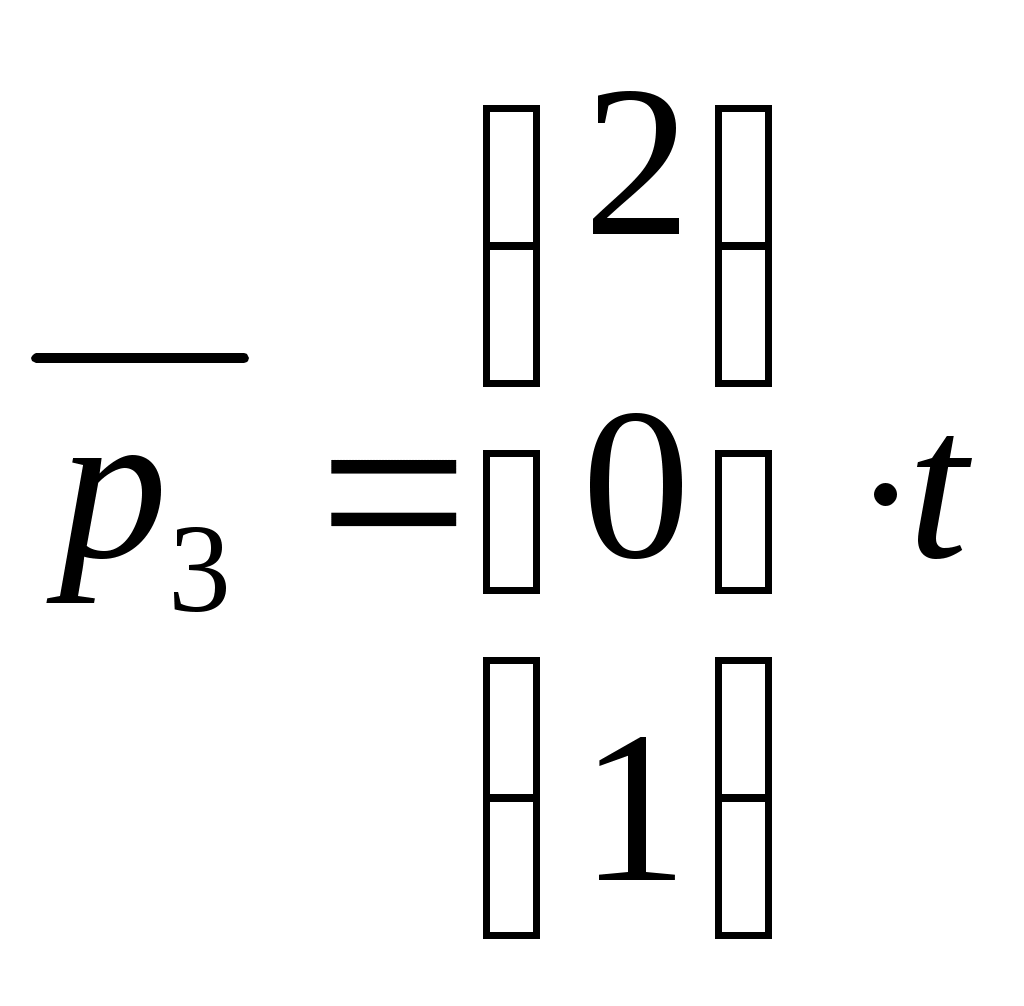 , где
, где Задание 1.80
Фирма имеет два магазина и торгует тремя товарами в течении года. Проводя расчёты в матричной форме, определить выручку магазинов от продаж каждого товара по сезонам. Ответ представить в виде таблицы. При этом стоимость единицы товара назначается различной в разные сезоны года:
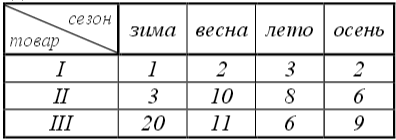
Объём продаж товаров трёх видов в двух магазинах в течении года представлен в таблицах:
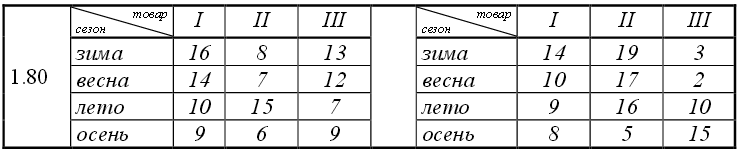
Решение
Для первого магазина:
Выручка для первого товара по сезонам:
Выручка для второго товара по сезонам:
Выручка для третьего товара по сезонам:
Заполним таблицу выручки продаж для первого магазина:
 Сезон СезонТовар | Зима | Весна | Лето | Осень |
| I | 16 | 28 | 30 | 18 |
| II | 24 | 70 | 120 | 36 |
| III | 260 | 132 | 42 | 81 |
Для второго магазина:
Выручка для первого товара по сезонам:
Выручка для второго товара по сезонам:
Выручка для третьего товара по сезонам:
Заполним таблицу выручки продаж для второго магазина:
 Сезон СезонТовар | Зима | Весна | Лето | Осень |
| I | 14 | 20 | 27 | 16 |
| II | 57 | 170 | 128 | 30 |
| III | 60 | 22 | 60 | 135 |
Задание 1.90
Вычислить комплексное число
Решение
Приводим к общему знаменателю
Умножим числитель и знаменатель на сопряжённый знаменателю множитель
.
Получили комплексное число в алгебраической форме:
Задание 1.100
Решить квадратное уравнение на множестве комплексных чисел
Решение
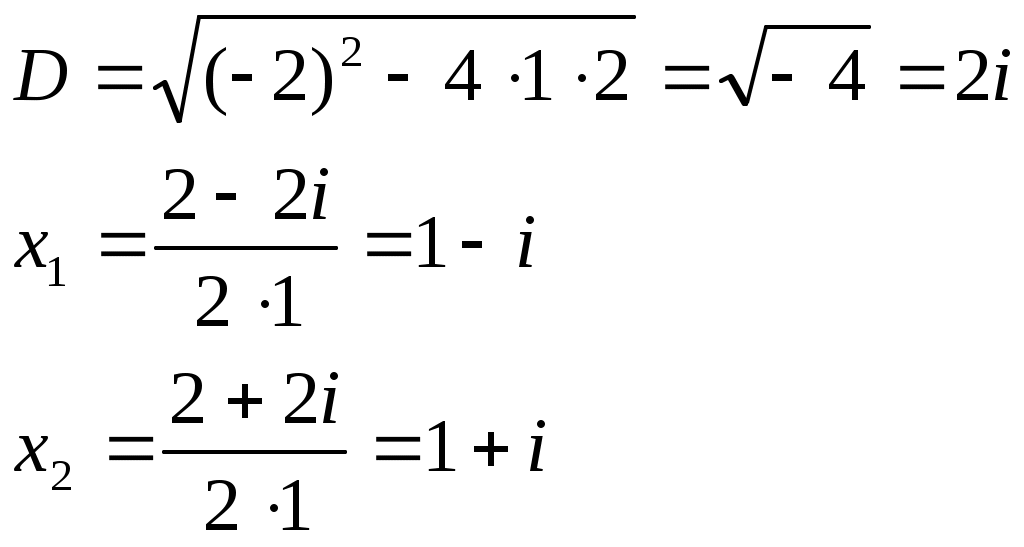
Ответ:
Задание 1.110
Вычислить все значения корня и построить их на комплексной плоскости
Решение
Находим тригонометрическую форму комплексного числа z = -8
x = Re(z) = -8
y = Im(z) = 0
Поскольку x < 0, y ≥ 0, то arg(z) находим как:
Таким образом, тригонометрическая форма комплексного числа z = -8
Извлекаем корни по формуле:
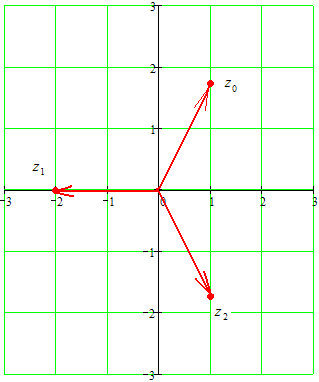
k = 0
или
=
k = 1
или
=-2
k = 2
или
=
Изобразим числа на комплексной плоскости
Задание 1.120
Дано комплексное число
а) записать число
б) изобразить
в) вычислить
г) найти все корни уравнения
д) вычислить произведение полученных корней