Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 599
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ван-дер-Ваальса, а в твердых телах еще и обменные (химические) силы. Силы Ван-дер-Ваальса удерживают молекулы жидкости друг возле друга на близких расстояниях порядка размера самих молекул. Если попытаться жидкость сжать, то при сближении молекул между ними начнут быстро нарастать силы отталкива- ния. Вследствие того, что молекулы расположены очень тесно, уже при незначи- тельном сближении силы отталкивания достигают очень большой величины.
Для упругих тел напряжения (силы, действующие на единичную площадь)прямо пропорциональны деформациям. Это закон Гука, который для жидкостей имеет вид:
p=-E V/V,
где p - сжимающее напряжение (гидростатическое давление), V - изменение объ- ёма, а V- первоначальный объём.
Величину сил отталкивания и характеризует модуль объемной упруго- сти E, который, например, для воды равен 2 109 Па. Нетрудно понять, что при сжатии твердых тел силы отталкивания еще больше (модуль объемной упругости для стали равен 2 1011Па).
Упругие силы возникают в твердых телах не только при объемном, но и при линейном сжатии. Например, если поместить пружину в некое гнездо, предвари- тельно уменьшив ее линейный размер на величину x,в ней возникает упругая си-
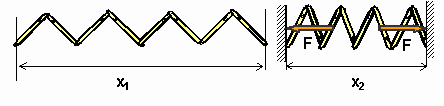ла F.
F = k x, где x- предвари- тельное поджатие пружи- ны, x=x1-x2, а k - коэффи- циент жесткости, завися- щий от материала пружи-
ны, ее размера и способа изготовления.
Так же просто объяснить, почему жидкость текуча и не способна сохранять свою форму. Под действием внешней силы перескоки молекул жидкости проис- ходят в направлении действия силы, и жидкость в результате течет. Однако необ-
ходимо, чтобы время действия силы было много больше времени оседлой жизни молекул, в противном случае сила вызовет лишь упругую деформацию сдвига и жидкость при этом будет тверда, как сталь (вязко-упругие жидкости).
Молекулы газа расположены далеко друг от друга и молекулярное притя- жение не властно над ними. Газообразное вещество не может сохранять не только форму, но и объем. Как бы мы не расширяли сосуд, содержащий газ, он заполнит его целиком без каких-либо усилий с нашей стороны.
Итак:
Твердые тела. Атомы твердого тела занимают определенное место в про- странстве, образуя кристаллическую решетку. Они расположены близко друг к другу и, вследствие молекулярных и химических сил, не в силах разорвать “пу- ты”, связывающие их с ближайшими соседями. Правда, из-за теплового движения они могут совершать колебания около положения равновесия. Твердое тело со- храняет постоянными объём и форму. Их трудно изменить, даже прикладывая к нему значительную силу.
Жидкости. Жидкость - беспорядочная, тесно сжатая “толпа” молекул, бес- покойно толкущихся на месте. Молекула жидкости, зажатая, как в клетке между другими молекулами, колеблется около положения равновесия. Лишь время от времени она совершает прыжок, прорываясь сквозь “прутья клетки”, но тут же попадает в новую клетку, образованную новыми соседями. Время оседлой жизни молекулы продолжается около десятимиллионной доли секунды.
Жидкости не противостоят напряжениям сдвига и не сохраняют постоянной формы. Они принимаюм форму сосуда, в котором находятся. Но, как и твердые тела, жидкости практически не поддаются сжатию и их объём можно изменить лишь с помощью очень большой силы.
Газы. Молекулы (или атомы) газа стремительно, как бегуны спринтеры, проносятся в пространстве, заполненном газом. Расстояния между ними значи- тельно превышают их собственные размеры, молекулярные силы отсутствуют. Непрерывно сталкиваясь друг с другом, молекулы газа резкими зигзагами броса- ются из стороны в сторону. Барабанная дробь бесчисленных молекул о стенки со- суда (равно как и о поверхность жидкости) создает давление.
Газы не
обладают ни определенной формой, ни определенным объёмом -
они полностью заполняют сосуды, в которых находятся.
Сила давления - мера взаимодействия между жидкостью и стенкой.
Она появляется потому, что жидкость на практике всегда находится в деформиро- ванном (сжатом) состоянии. На неё действуют собственный вес, реакции стенок и другие сжимающие силы . В результате деформации в жидкости появляется сжи- мающее напряжение, которое мы называем абсолютным давлением.
Необходимо определить силу давления жидкости на поверхность, имею- щую ось симметрии и наклоненную под углом к горизонту. Форма поверхности значения не имеет. Она может быть круглой, треугольной, прямоугольной, трапе- цеидальной.
Абсолютное давление на поверхности контакта между жидкостью и стен- кой определяет степень сжатия жидкости в окрестности точки. По III-му закону Ньютона сжатая жидкость оказывает на поверхность такое же давление, но с про- тивоположным знаком (аналогия со сжатой пружиной). Сумма воздействий жид- кости на поверхность во всех её точках определяет суммарное давление на по- верхность, или силу давления.
Рассмотрим простейший случай, когда резервуар открытый, и на свободную поверхность жидкости действует атмосферное давление. Атмосферное давление передается по закону Паскаля через жидкость и действует на стенку изнутри. Так как снаружи также действует атмосферное давление, то в результате оно уравно- вешивается и не влияет на стенку.
Итак: в открытом резервуаре соприкасающие с жидкостью поверхности находят- ся под воздействием только весового давления (давления столба жидкости).
Сила давления столба жидкости - это вектор. Сила давления характеризуется величиной (модулем), направлением и точкой приложения.
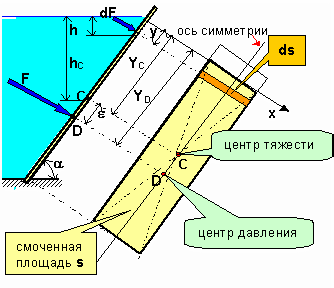.F = рC s =ghCs , где hC- глубина погружения в жидкость центра тяжести площади стенки s. Для доказательства разобъём смоченную жидкостью площадь s на площадки величиной ds, которые ввиду малости можно считать горизонтальными. Во всех точках такой площадки давление столба жидкости можно считать одинаковым и равным =gh. На площадку ds действует со стороны жидкости сила dF = р s =ghds. На всю площадь s будет действовать множество параллельных сил dF
(увеличивающихся с глубиной из-за роста h). Результирующая сила F представ- ляет собой алгебраическую сумму составляющих сил dF, то есть интеграл:
F dF g h ds g Sin y ds.
где y - расстояние от любой площадки до поверхности жидкости, отсчитываемое в плоскости стенки. Произведение yds есть статический момент площади ds относи- тельно оси х(ось х - линия пересечения поверхности жидкости с плоскостью
стенки - линия уреза жидкости). Сумма таких произведений (интеграл) для всех площадок равна статическому моменту всей площади относительно оси х:
y ds yC s.
где yC- расстояние до центра тяжести площади s, отсчитываемое в плоскости стенки.
Окончательно получим: .F=gSin yCs=ghCs.
Замечая, что ghCесть дав- ление в центре тяжести стенки (в точке С), окончательно получим:
F = рC s .
Принципиальный вопрос: где же должна быть расположена точка прило- жения равнодействующей силы - выше или ниже центра тяжести площади стенки?
Ответ: ниже, поскольку с глубиной силы давления dF увеличиваются, а точка приложения равнодействующей параллельных сил всегда сдвигается к большей силе (теорема Вариньона - известный факт из теоретической механики). Теорема Вариньона
Момент равнодействующей силы относительно произвольной точки (оси) равенсуммемоментовсоставляющихсилотносительно этойточки (оси).
Чтобы узнать, насколько ниже центра тяжести стенки приложена равнодей- ствующая сила (определить величину e ), применим теорему Вариньона относи- тельно оси х. Здесь F - результирующая сила, её плечо равно yD, dF - составляю- щие силы, плечо равно y.
F yD
dF y gh y ds g Sin y2 ds g Sin Ix.
Здесь IX= y2ds- момент инерции площади s относительно оси х.
Подставляя выражение для силы F и представляя момент инерции относительно оси х как сумму момента инерции относительно центральной оси и произведения площади на квадрат расстояния между осями IX=IC+yC2 s,получим:
Для упругих тел напряжения (силы, действующие на единичную площадь)прямо пропорциональны деформациям. Это закон Гука, который для жидкостей имеет вид:
p=-E V/V,
где p - сжимающее напряжение (гидростатическое давление), V - изменение объ- ёма, а V- первоначальный объём.
Величину сил отталкивания и характеризует модуль объемной упруго- сти E, который, например, для воды равен 2 109 Па. Нетрудно понять, что при сжатии твердых тел силы отталкивания еще больше (модуль объемной упругости для стали равен 2 1011Па).
Упругие силы возникают в твердых телах не только при объемном, но и при линейном сжатии. Например, если поместить пружину в некое гнездо, предвари- тельно уменьшив ее линейный размер на величину x,в ней возникает упругая си-
ла F.F = k x, где x- предвари- тельное поджатие пружи- ны, x=x1-x2, а k - коэффи- циент жесткости, завися- щий от материала пружи-
ны, ее размера и способа изготовления.
Так же просто объяснить, почему жидкость текуча и не способна сохранять свою форму. Под действием внешней силы перескоки молекул жидкости проис- ходят в направлении действия силы, и жидкость в результате течет. Однако необ-
ходимо, чтобы время действия силы было много больше времени оседлой жизни молекул, в противном случае сила вызовет лишь упругую деформацию сдвига и жидкость при этом будет тверда, как сталь (вязко-упругие жидкости).
Молекулы газа расположены далеко друг от друга и молекулярное притя- жение не властно над ними. Газообразное вещество не может сохранять не только форму, но и объем. Как бы мы не расширяли сосуд, содержащий газ, он заполнит его целиком без каких-либо усилий с нашей стороны.
Итак:
Твердые тела. Атомы твердого тела занимают определенное место в про- странстве, образуя кристаллическую решетку. Они расположены близко друг к другу и, вследствие молекулярных и химических сил, не в силах разорвать “пу- ты”, связывающие их с ближайшими соседями. Правда, из-за теплового движения они могут совершать колебания около положения равновесия. Твердое тело со- храняет постоянными объём и форму. Их трудно изменить, даже прикладывая к нему значительную силу.
Жидкости. Жидкость - беспорядочная, тесно сжатая “толпа” молекул, бес- покойно толкущихся на месте. Молекула жидкости, зажатая, как в клетке между другими молекулами, колеблется около положения равновесия. Лишь время от времени она совершает прыжок, прорываясь сквозь “прутья клетки”, но тут же попадает в новую клетку, образованную новыми соседями. Время оседлой жизни молекулы продолжается около десятимиллионной доли секунды.
Жидкости не противостоят напряжениям сдвига и не сохраняют постоянной формы. Они принимаюм форму сосуда, в котором находятся. Но, как и твердые тела, жидкости практически не поддаются сжатию и их объём можно изменить лишь с помощью очень большой силы.
Газы. Молекулы (или атомы) газа стремительно, как бегуны спринтеры, проносятся в пространстве, заполненном газом. Расстояния между ними значи- тельно превышают их собственные размеры, молекулярные силы отсутствуют. Непрерывно сталкиваясь друг с другом, молекулы газа резкими зигзагами броса- ются из стороны в сторону. Барабанная дробь бесчисленных молекул о стенки со- суда (равно как и о поверхность жидкости) создает давление.
Газы не
обладают ни определенной формой, ни определенным объёмом -
они полностью заполняют сосуды, в которых находятся.
-
СИЛА ДАВЛЕНИЯ СТОЛБА ЖИДКОСТИ
Сила давления - мера взаимодействия между жидкостью и стенкой.
Она появляется потому, что жидкость на практике всегда находится в деформиро- ванном (сжатом) состоянии. На неё действуют собственный вес, реакции стенок и другие сжимающие силы . В результате деформации в жидкости появляется сжи- мающее напряжение, которое мы называем абсолютным давлением.
Необходимо определить силу давления жидкости на поверхность, имею- щую ось симметрии и наклоненную под углом к горизонту. Форма поверхности значения не имеет. Она может быть круглой, треугольной, прямоугольной, трапе- цеидальной.
Абсолютное давление на поверхности контакта между жидкостью и стен- кой определяет степень сжатия жидкости в окрестности точки. По III-му закону Ньютона сжатая жидкость оказывает на поверхность такое же давление, но с про- тивоположным знаком (аналогия со сжатой пружиной). Сумма воздействий жид- кости на поверхность во всех её точках определяет суммарное давление на по- верхность, или силу давления.
Рассмотрим простейший случай, когда резервуар открытый, и на свободную поверхность жидкости действует атмосферное давление. Атмосферное давление передается по закону Паскаля через жидкость и действует на стенку изнутри. Так как снаружи также действует атмосферное давление, то в результате оно уравно- вешивается и не влияет на стенку.
Итак: в открытом резервуаре соприкасающие с жидкостью поверхности находят- ся под воздействием только весового давления (давления столба жидкости).
Сила давления столба жидкости - это вектор. Сила давления характеризуется величиной (модулем), направлением и точкой приложения.
-
Направление силы всегда перпендикулярно площади стенки. -
Величина силы равна произведению площади стенки на давление в центре тяжести этой площади.
.F = рC s =ghCs , где hC- глубина погружения в жидкость центра тяжести площади стенки s. Для доказательства разобъём смоченную жидкостью площадь s на площадки величиной ds, которые ввиду малости можно считать горизонтальными. Во всех точках такой площадки давление столба жидкости можно считать одинаковым и равным =gh. На площадку ds действует со стороны жидкости сила dF = р s =ghds. На всю площадь s будет действовать множество параллельных сил dF(увеличивающихся с глубиной из-за роста h). Результирующая сила F представ- ляет собой алгебраическую сумму составляющих сил dF, то есть интеграл:
F dF g h ds g Sin y ds.
где y - расстояние от любой площадки до поверхности жидкости, отсчитываемое в плоскости стенки. Произведение yds есть статический момент площади ds относи- тельно оси х(ось х - линия пересечения поверхности жидкости с плоскостью
стенки - линия уреза жидкости). Сумма таких произведений (интеграл) для всех площадок равна статическому моменту всей площади относительно оси х:
y ds yC s.
где yC- расстояние до центра тяжести площади s, отсчитываемое в плоскости стенки.
Окончательно получим: .F=gSin yCs=ghCs.
Замечая, что ghCесть дав- ление в центре тяжести стенки (в точке С), окончательно получим:
F = рC s .
-
Определение точки приложения силы давления (центра давления) Сила F пересекает площадь стенки в точке D, которая называется центр давле- ния. Положение точки на плоскости определяется двумя координатами. Для сим- метричных стенок точка D должна лежать на оси симметрии.
Принципиальный вопрос: где же должна быть расположена точка прило- жения равнодействующей силы - выше или ниже центра тяжести площади стенки?Ответ: ниже, поскольку с глубиной силы давления dF увеличиваются, а точка приложения равнодействующей параллельных сил всегда сдвигается к большей силе (теорема Вариньона - известный факт из теоретической механики). Теорема Вариньона
Момент равнодействующей силы относительно произвольной точки (оси) равенсуммемоментовсоставляющихсилотносительно этойточки (оси).
Чтобы узнать, насколько ниже центра тяжести стенки приложена равнодей- ствующая сила (определить величину e ), применим теорему Вариньона относи- тельно оси х. Здесь F - результирующая сила, её плечо равно yD, dF - составляю- щие силы, плечо равно y.
F yD
dF y gh y ds g Sin y2 ds g Sin Ix.
Здесь IX= y2ds- момент инерции площади s относительно оси х.
Подставляя выражение для силы F и представляя момент инерции относительно оси х как сумму момента инерции относительно центральной оси и произведения площади на квадрат расстояния между осями IX=IC+yC2 s,получим: