Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 602
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
р0+gh; (1)
рвес.=gh, (2)
где рвес– давление за счет веса жидкости (весовое давление или давление столба жидкости). Давление газа р0передается через жидкость на глубину h по закону Паскаля.
Основное уравнение гидростатики (1) связывает давления на двух горизон- тальных плоскостях в жидкости.
Закон Паскаля: Давление р0, созданное на жидкость любым путем, передаетсявовсе точки объёмажидкостибез изменения.
Манометр – измеряет избыток абсолютного давления над атмосферным.
рм=р-рат. (3)
Вакуумметр - измеряет недостаток абсолютного давления до атмосферного.
рv=рат–р. (4)
Используя показания приборов, можно определить абсолютное давление по формулам пересчета (5) и (6).
р = рат + рм; (5)
р=рат-рv. (6)
 Атмосферное давление ратопределяется по барометру. Если ратне задано, оно принимается равным: рат=105Па=0,1МПа.
Атмосферное давление ратопределяется по барометру. Если ратне задано, оно принимается равным: рат=105Па=0,1МПа.
Возвращаемся к решению задачи.
р = рат- рv0- если давление газа меньше атмосферного и прибор показы- вает рv0.
рH
=р0+gH=рат+ рм0+gH-если давление газа больше атмосфер-
ного;
рH=р0+gH=рат– рv0+gH-если давление газа больше атмосфер- ного.
рмH=рH-рат=рат+ рм0+gH-рат= рм0+gH-если давление газа больше атмосферного;
 рмH=рH-рат=рат– рv0+gH-рат= - рv0+gH-если давление газа меньше атмосферного.
рмH=рH-рат=рат– рv0+gH-рат= - рv0+gH-если давление газа меньше атмосферного.
Как определяется сила, с которой жидкость давит на соприка- сающуюся с ней поверхность?
Поверхности, с которыми соприкасается жидкость, бывают плоские и криволинейные (в большинстве случаев цилиндрические или сфери- ческие).
Сила давления – вектор. Необходимо определить модуль силы, её на- правление и точку приложения. Методика определения сил давления на криво- линейные поверхности здесь не рассматривается.
Для плоских поверхностей сила давления всегда перпендикулярна по-верхности(Рис.3, 3есвойство давления).
Рассмотрим простейший случай, когда сосуд открытый, и на свободную поверхность жидкости действует атмосферное давление (Рис.4).
Абсолютное давление в жидкости в данном случае на произвольной глу- бине hравно:
рh=рат+gh.
Атмосферное давление передается по закону Паскаля через жидкость и действует на крышку изнутри. Так как снаружи также действует атмосферное давление, то в результате оно уравновешивается и не влияет на крышку.
рат
h0
H
Fж
рат
c
d
эпюра давления ось симметрии
 cмоченная жидкостью площадь крышки (s)
cмоченная жидкостью площадь крышки (s)
k
m
центр тяжести площади s (точка с)
Рис. 4
центр давления площади s (точка d)
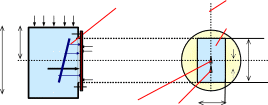
Определение силы давления жидкости для открытого сосуда
Таким образом, в открытом сосуде соприкасающие с жидкостью поверх- ности находятся под воздействием только весового давления.
На Рис.4 показано распределение весового давления по контуру стенки, которое называется эпюрой. Из теоретической механики известна связь между распределенной нагрузкой и сосредоточенной силой. Итак, графоаналитический способ:
Давление – распределенная нагрузка на поверхность. Сила давления равнаобъёму эпюры давления. Линия действия силы проходит через центр тяжестиобъёма эпюры. Точка пересечения линии действия силы давления и плоскостистенки– центр давления(точка d).
Суммарная сила давления на стенку в данном случае равна силе весового давления жидкости, так как силы атмосферного давления с обеих сторон стенки уравновещиваются.
F =Fж.
На практике, если стенка переменной ширины (например, круглая как в данном случае), определить объём эпюры затруднительно. Поэтому используется аналитический способ.
Этот способ описан в разделе 2.1.3 данного учебного пособия.
Модуль (величина) силы весового давления определяется так:
Fж=рсs=ghcs; (7)
рс=ghc,, (8)
где рс- давление в центре тяжести площади s,s -площадь смоченной поверхно- сти стенки;
hc– глубина погружения центра тяжести под уровень свободной поверхно- сти (расстояние по вертикали от свободной поверхности до центра тяжести).
ВНИМАНИЕ!
Площадь крышки по форме и по величине отличается от площади s, смо- ченной жидкостью. При определении силы давления в формулу следует под- ставлять смоченную площадь, которая равна площади отверстия.
Направлениесилы: всегда перпендикулярно поверхности.
Координаты точки приложения силы (центра давления) – это координаты точки на плоскости.
Положение точки на плоскости определяется двумя координатами.
(Рис.4) определяется так:
cd
Ic
s lc
, (9)
где Ic–момент инерции площади sотносительно горизонтальной оси (справоч-
ная величина, Приложение 1).
В данном случае Ic= mk3/12; lc–расстояние по контуру стенки от центра тяжести площади s до свободной поверхности жидкости.
В нашей задаче lc= h0.
ВНИМАНИЕ!
Если стенка не является вертикальной, lc h0! В нашей задаче:
mk3
12km h0
k2
.
12 h0
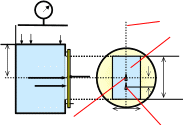
 Что изменится, если резервуар закрыт и на свободной поверхности жидкости давление не равно атмосферному (как в нашей задаче, Рис.1)?
Что изменится, если резервуар закрыт и на свободной поверхности жидкости давление не равно атмосферному (как в нашей задаче, Рис.1)?
Величина силы давления будет определяться по формуле :
F=рс ; (10)
рс=р0+gh–рат, (11) где рс– результирующее давление в центре тяжести площади s(с учетом про- тиводействующего атмосферного давления с другой стороны).
Но в этом случае величину нельзя определять по формуле (9).
cd
Ic !
s lc
Формула (9) выведена для случая р0= рат.
Точка приложения равнодействующей силы для закрытого сосуда опре- деляется по правилам сложения параллельных сил.
Сила давления жидкости на стенку слева (изнутри) Fлевразбивается на
две параллельные силы – силу внешнего давления F0и силу весового давления жидкости Fж.
Fлев.=рс s=(р0+gh) s=р0 s+gh s=F0+ Fж.
 С внешней стороны стенки действует сила атмосферного давления. Опре- деляются по отдельности эти силы и точки их приложения. Далее находится суммарная сила как равнодействующая системы параллельных сил (Рис. 7).
С внешней стороны стенки действует сила атмосферного давления. Опре- деляются по отдельности эти силы и точки их приложения. Далее находится суммарная сила как равнодействующая системы параллельных сил (Рис. 7).
рвес.=gh, (2)
где рвес– давление за счет веса жидкости (весовое давление или давление столба жидкости). Давление газа р0передается через жидкость на глубину h по закону Паскаля.
Основное уравнение гидростатики (1) связывает давления на двух горизон- тальных плоскостях в жидкости.
Закон Паскаля: Давление р0, созданное на жидкость любым путем, передаетсявовсе точки объёмажидкостибез изменения.
Манометр – измеряет избыток абсолютного давления над атмосферным.
рм=р-рат. (3)
Вакуумметр - измеряет недостаток абсолютного давления до атмосферного.
рv=рат–р. (4)
Используя показания приборов, можно определить абсолютное давление по формулам пересчета (5) и (6).
р = рат + рм; (5)
р=рат-рv. (6)
 Атмосферное давление ратопределяется по барометру. Если ратне задано, оно принимается равным: рат=105Па=0,1МПа.
Атмосферное давление ратопределяется по барометру. Если ратне задано, оно принимается равным: рат=105Па=0,1МПа.Возвращаемся к решению задачи.
-
Определяем абсолютное давление газа по показанию мановакуумметра: р = рат+ рм0- если давление газа больше атмосферного и прибор показы- вает рм0;
р = рат- рv0- если давление газа меньше атмосферного и прибор показы- вает рv0.
-
Определяем абсолютное давление в жидкости на глубине H по уравне- нию (1):
рH
=р0+gH=рат+ рм0+gH-если давление газа больше атмосфер-
ного;
рH=р0+gH=рат– рv0+gH-если давление газа больше атмосфер- ного.
-
Определяем показание манометра рмH:
рмH=рH-рат=рат+ рм0+gH-рат= рм0+gH-если давление газа больше атмосферного;
 рмH=рH-рат=рат– рv0+gH-рат= - рv0+gH-если давление газа меньше атмосферного.
рмH=рH-рат=рат– рv0+gH-рат= - рv0+gH-если давление газа меньше атмосферного.
Как определяется сила, с которой жидкость давит на соприка- сающуюся с ней поверхность?
Поверхности, с которыми соприкасается жидкость, бывают плоские и криволинейные (в большинстве случаев цилиндрические или сфери- ческие).
Сила давления – вектор. Необходимо определить модуль силы, её на- правление и точку приложения. Методика определения сил давления на криво- линейные поверхности здесь не рассматривается.
Для плоских поверхностей сила давления всегда перпендикулярна по-верхности(Рис.3, 3есвойство давления).
-
ОПРЕДЕЛЕНИЕ СИЛЫ ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКУЮ ПОВЕРХНОСТЬ
Рассмотрим простейший случай, когда сосуд открытый, и на свободную поверхность жидкости действует атмосферное давление (Рис.4).
Абсолютное давление в жидкости в данном случае на произвольной глу- бине hравно:
рh=рат+gh.
Атмосферное давление передается по закону Паскаля через жидкость и действует на крышку изнутри. Так как снаружи также действует атмосферное давление, то в результате оно уравновешивается и не влияет на крышку.
рат
h0
H
Fж
рат
c
d
эпюра давления ось симметрии
 cмоченная жидкостью площадь крышки (s)
cмоченная жидкостью площадь крышки (s)k
m
центр тяжести площади s (точка с)
Рис. 4
центр давления площади s (точка d)
Определение силы давления жидкости для открытого сосуда
Таким образом, в открытом сосуде соприкасающие с жидкостью поверх- ности находятся под воздействием только весового давления.
-
Графоаналитический способ определения силы и центра давления
На Рис.4 показано распределение весового давления по контуру стенки, которое называется эпюрой. Из теоретической механики известна связь между распределенной нагрузкой и сосредоточенной силой. Итак, графоаналитический способ:
Давление – распределенная нагрузка на поверхность. Сила давления равнаобъёму эпюры давления. Линия действия силы проходит через центр тяжестиобъёма эпюры. Точка пересечения линии действия силы давления и плоскостистенки– центр давления(точка d).
Суммарная сила давления на стенку в данном случае равна силе весового давления жидкости, так как силы атмосферного давления с обеих сторон стенки уравновещиваются.
F =Fж.
На практике, если стенка переменной ширины (например, круглая как в данном случае), определить объём эпюры затруднительно. Поэтому используется аналитический способ.
-
Аналитический способ определения силы и центра давления
Этот способ описан в разделе 2.1.3 данного учебного пособия.
Модуль (величина) силы весового давления определяется так:
Fж=рсs=ghcs; (7)
рс=ghc,, (8)
где рс- давление в центре тяжести площади s,s -площадь смоченной поверхно- сти стенки;
hc– глубина погружения центра тяжести под уровень свободной поверхно- сти (расстояние по вертикали от свободной поверхности до центра тяжести).
ВНИМАНИЕ!
Площадь крышки по форме и по величине отличается от площади s, смо- ченной жидкостью. При определении силы давления в формулу следует под- ставлять смоченную площадь, которая равна площади отверстия.
Направлениесилы: всегда перпендикулярно поверхности.
Координаты точки приложения силы (центра давления) – это координаты точки на плоскости.
Положение точки на плоскости определяется двумя координатами.
-
Центр давления точка dлежит на оси симметрии стенки. -
Расстояние по оси симметрии от центра тяжести до центра давления
(Рис.4) определяется так:
cd
Ic
s lc
, (9)
где Ic–момент инерции площади sотносительно горизонтальной оси (справоч-
ная величина, Приложение 1).
В данном случае Ic= mk3/12; lc–расстояние по контуру стенки от центра тяжести площади s до свободной поверхности жидкости.
В нашей задаче lc= h0.
ВНИМАНИЕ!
Если стенка не является вертикальной, lc h0! В нашей задаче:
mk3
12km h0
k2
.
12 h0
 Что изменится, если резервуар закрыт и на свободной поверхности жидкости давление не равно атмосферному (как в нашей задаче, Рис.1)?
Что изменится, если резервуар закрыт и на свободной поверхности жидкости давление не равно атмосферному (как в нашей задаче, Рис.1)?Величина силы давления будет определяться по формуле :
F=рс ; (10)
рс=р0+gh–рат, (11) где рс– результирующее давление в центре тяжести площади s(с учетом про- тиводействующего атмосферного давления с другой стороны).
Но в этом случае величину нельзя определять по формуле (9).
cd
Ic !
s lc
Формула (9) выведена для случая р0= рат.
Точка приложения равнодействующей силы для закрытого сосуда опре- деляется по правилам сложения параллельных сил.
-
Определение суммарной силы давления как равнодействующей системы параллельных сил
Сила давления жидкости на стенку слева (изнутри) Fлевразбивается на
две параллельные силы – силу внешнего давления F0и силу весового давления жидкости Fж.
Fлев.=рс s=(р0+gh) s=р0 s+gh s=F0+ Fж.
 С внешней стороны стенки действует сила атмосферного давления. Опре- деляются по отдельности эти силы и точки их приложения. Далее находится суммарная сила как равнодействующая системы параллельных сил (Рис. 7).
С внешней стороны стенки действует сила атмосферного давления. Опре- деляются по отдельности эти силы и точки их приложения. Далее находится суммарная сила как равнодействующая системы параллельных сил (Рис. 7).