Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 601
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
D
y g Sin Ix
g Sin (IC
s l2 ) I
C lC C
F g hC s s yC
Расстояние от центра тяжести до точки приложения силы =yD-yCопределяется так.
IC .s yC
где Ic- момент инерции площади стенки относительно горизонтальной централь- ной оси. Это справочная величина, например для круга IC=d4/64. Величина yC равна расстоянию от центра тяжести до свободной поверхности жидкости (по оси симметрии стенки).
Очень важно!
F = рС s.
При определении величины силы в формулу под- ставляется давление в центре тяжести (в точке С), а сама сила приложена в центре давления (в точке D).
Распространенная студенческая ошибка: .F = рD s . Кажется, с точки зрения "здравого смысла", что нужно подставлять в эту формулу давление в той же точке, где приложена сила. Это неверно.
РАЗДЕЛ3
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ГИДРОСТАТИКИ
Методику решения задач гидростатики рассмотрим на примере решения конкретной задачи.
-
ПОСТАНОВКА ЗАДАЧИ
В резервуаре над жидкостью плотностью находится газ. Давление газа р0может быть больше, чем атмосферное – тогда показание мановакуумметра равно рм0.Если давление газа меньше, чем атмосферное - показание прибора равно рv0.
В боковой стенке резервуара имеется прямоугольное отверстие с размерами k m. Центр тяжести отверстия находится на глубине h0под уровнем свободной поверхности жидкости (поверхности контакта жидкости с газом). Отверстие за- крыто круглой крышкой 1, которая может поворачиваться вокруг оси А против часовой стрелки под действием момента от силы давления жидкости. Чтобы крышка не поворачивалась, к ней приложена сила R. Размеры a и b фиксируют положение оси вращения и точки приложения силы относительно центра тяжести отверстия.
В дне резервуара, на глубине H расположено круглое отверстие диаметра d. Отверстие закрыто крышкой 2, которая крепится болтами к резервуару. pмH– по- казание манометра, который установлен на уровне дна резервуара.
Дано: ;рм0(pv0);h0;H;a;b;k;m.
Определить:
-
Давление р0. -
Показание рмH. -
Силу R. -
Силу F2, отрывающую болты крышки.
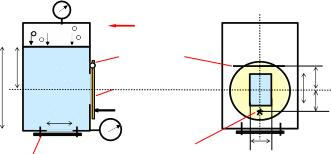мановакуумметрр0
h0
H
d
рм0 (pv0)
Y
R
ось вращения крышка 1
рмH
вид по стрелке Y
a
k
b
крышка 2
точка приложения силы R m
Рис.1
Схема к задаче
Откуда берутся силы, действующие со стороны жидкости на крыш- ки?Жидкость находится в неподвижном состоянии под силовым воздействи- ем. Жидкость сжата со всех сторон силами реакции окружающих поверхностей, силой давления со стороны газа и собственным весом. В результате в ней возни- кают сжимающие напряжения (Рис.2).
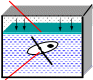свободная поверхность жидкости под давлением р0dF1
A
dF2
площадь s
Рис.2
Определение давления
Выделим внутри жидкости вокруг точки А площадку ds. Сила dF1характеризует действие частиц, находящихся вверху площадки, а сила dF2- находящихся вни- зу площадки.
Вектор напряжения – предел отношения элементарной силы dFк площади ds при стремлении площади ds к нулю с сохра- нением ориентации площадки
р limdF.
ds0 ds
Вектор напряжения зависит от ориентации площадки. Их число – бесчис- ленное множество. Каждый вектор может иметь нормальную по отношению к площадке и касательную составляющую. В покоящейся жидкости отсутствуют касательные напряжения, и расстояния между молекулами в данной точке одина-
ковы по всем направлениям (так как в жидкости нет структуры). Поэтому напря- жение в точке внутри жидкости это не вектор, а скалярная величина (не завися- щая от направления).
Абсолютное гидростатическое давление – модуль вектора сжимающего напря- жения в жидкости., а модули нормальных напряжений на всех площадках, прохо- дящих через точку А, равны между собой и называются абсолютным гидростати- ческим давлением.
р p
lim .
ds0 dsДавление – скалярная величина, имеющая размерность напряжения.
p
сила н площадь м2
Па .
Свойства гидростатического давления
газРис.3
Иллюстрация к свойствам гидростатического давления
-
Во всех точках горизонтальной площади, проведенной через однородную жидкость, давление одинаково.
-
В данной точке внутри жидкости давление по всем направлениям одина- ково. Это означает, что давление в жидкости на определенном уровнеможноопределятьисверху,иснизу, ислева, исправа. -
На внешней поверхности жидкости давление направлено перпендику- лярно к поверхности. В противном случае на жидкость действовали бы касательные силы и она бы двигалась. -
При перемещении в жидкости сверху вниз давление увеличивается:
р3 > р2 > р1 > р0 .
Молекулы жидкости, стремясь освободиться от сжимающих напряжений, в свою очередь оказывают силовое воздействие на окружающие поверхности (3ий закон Ньютона – действие равно противодействию!). В
результате и возникают силы давления на крышки в нашей задаче.
Давление в газе
В идеальном газе отсутствуют связи между молекулами, поэтому давление газа имеет совсем другой физический смысл, чем давление в жидкости. Молекулы газа совершают хаотическое (броуновское) движение. При этом они ударяются о поверхность жидкости и теряют свой импульс. Как известно из теоретической ме- ханики, при изменении импульса появляется сила, в данном случае это сила дав- ления газа на поверхность жидкости. Единичная (на единицу площади) силадавленияиестьдавление газа.
Состояние газа определяется тремя параметрами – абсолютным давлением р, плотностью и абсолютной температурой T, которые связаны уравнением со- стояния (уравнением Клапейрона).
pV=mRT,
где R–газовая постоянная, R=287дж/кгК для воздуха.
Уравнение состояния можно записать в виде:
p/ =RT.
При увеличении температуры усиливается броуновское движение молекул и частота их ударов о поверхность. При этом давление газа увеличивается.
Вмалыхобъёмахдавлениегазаодинаковововсехточкахобъёма.Вбольших объёмах давление газа уменьшается с высотой по экспотенциально-музакону.
-
ВЫЧИСЛЕНИЕ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ
Абсолютное давление в жидкости можно вычислить по формуле (1), кото- рая называется основным уравнением гидростатики, а также можно измерить с помощью приборов - мановакуумметров.
p=