Файл: Методические указания и контрольные задания по дисциплине информационная безопасность для студентов направления 09. 03. 02.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 1113
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, получим следующую систему подстановок:
0 3
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
Ъ Э Ю К А Д Ы М О Т Е Ч С В Н Л И П Р Я Б Г Ж З Й У Ф Х Ц Ш Щ Ь
Достоинством системы Цезаря с ключевым словом является то, что количество возможных ключевых слов практически неисчерпаемо. Недостатком этой системы является возможность взлома шифртекста на основе анализа частот появления букв.
В 1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием "Полиграфия". В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. При шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже неё в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самая верхнюю букву из того же столбца.
Задача 1.9. Зашифровать таблицей Трисемуса сообщение:
ВЫЛЕТАЕМ ПЯТОГО
Решение. Для русского алфавита шифрующая таблица может иметь размер 48. Шифрующая таблица выглядит так:
Рисунок 1.5 - Шифрующая таблица Трисемуса с ключевым словом БАНДЕРОЛЬ
Используя эту таблицу в соответствии с вышеизложенной методикой
, получаем шифртекст
ПДКЗЫВЗЧШЛЫЙСЙ.
Такие табличные шифры называются монограммными, так как шифрование выполняется по одной букве. Трисемус первым заметил, что шифрующие таблицы позволяют шифровать сразу по две буквы. Такие шифры называются биграммными.
Задача 3.1.
Пусть выбраны простые числа р =47 и q=71 и открытый ключ е=79.
Требуется выполнить шифрование и дешифрование в асимметричной криптосистеме RSA сообщения:
688 232 687 966 668 3
Укажите последовательность операций.
Решение.
1.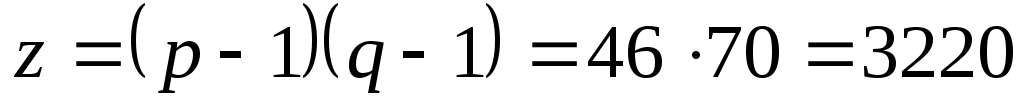
2. Найдём секретный ключ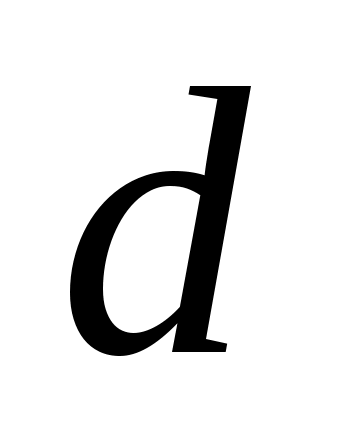 в результате решения сравнения:
в результате решения сравнения:
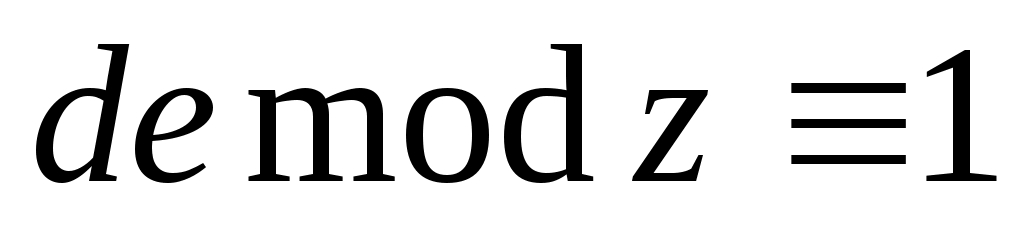 ,
,
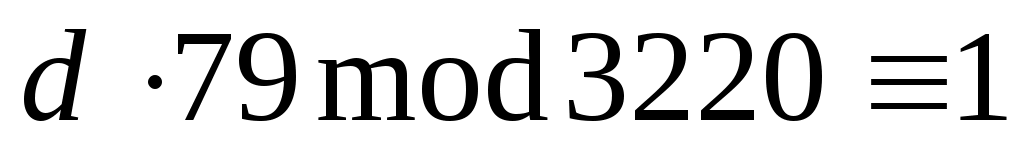 .
.
Воспользуемся расширенным алгоритмом Евклида:
79=3220*0+79,
3220=79*40+60,
79=60*1+19,
60=19*3+3,
19=3*6+1,
3=1*3+0.
Результаты вычислений сведём в таблицу:
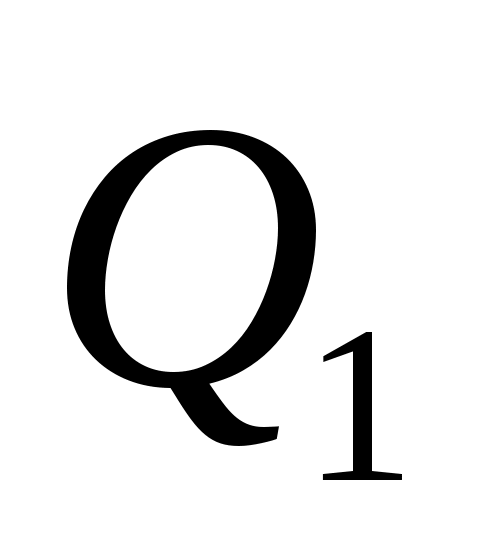
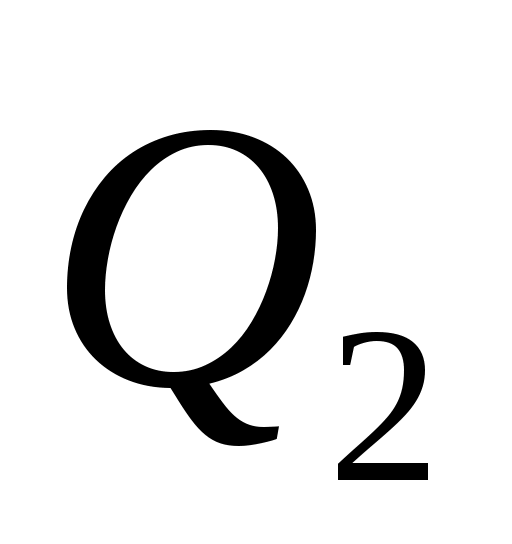
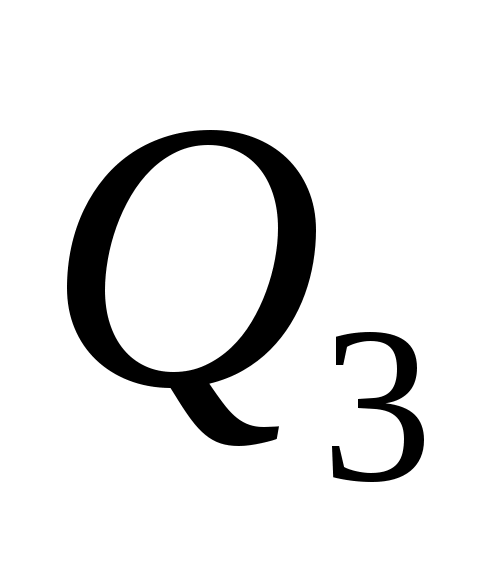
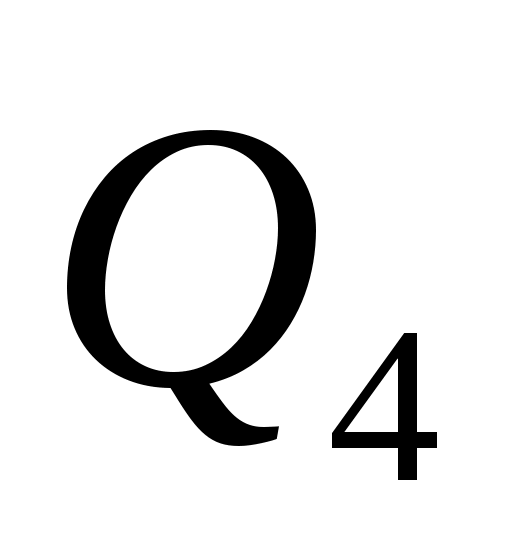
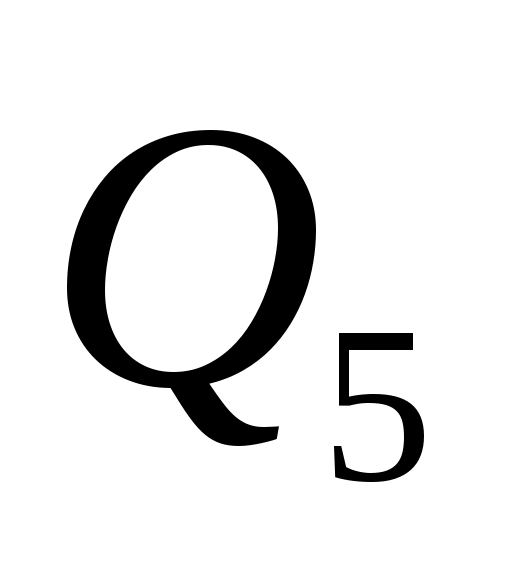 .
.
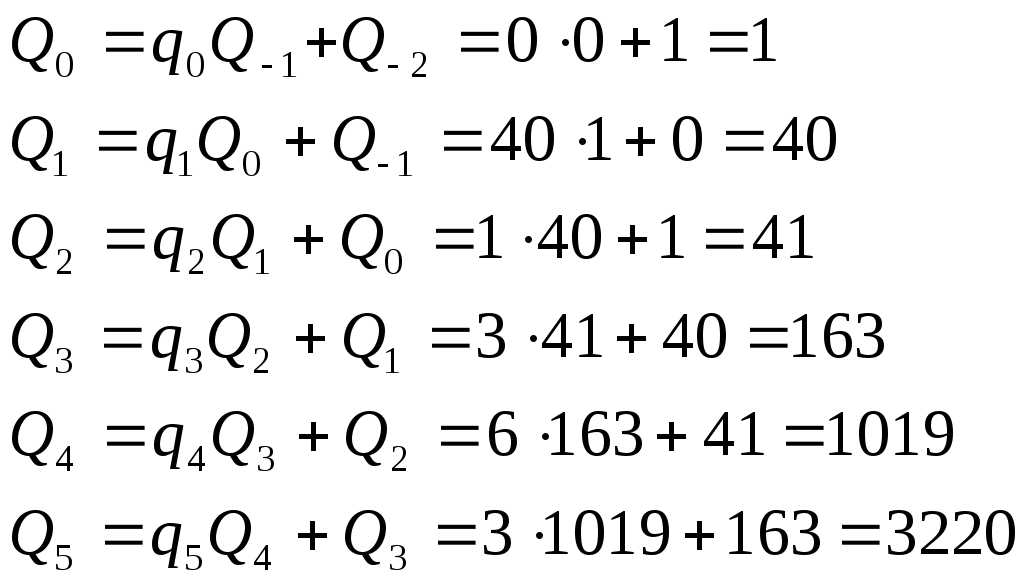
к=5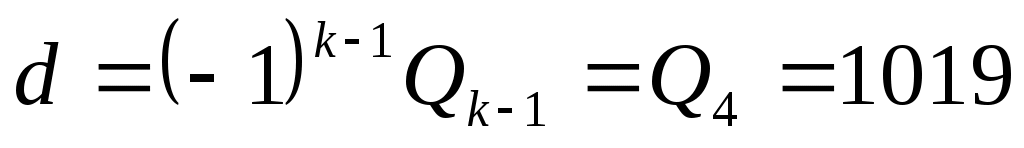
В самом деле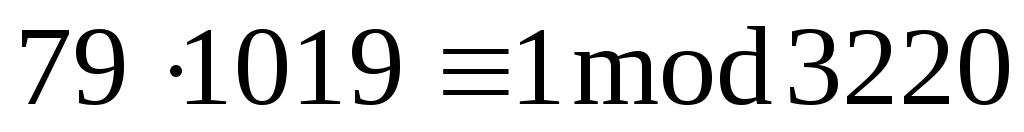
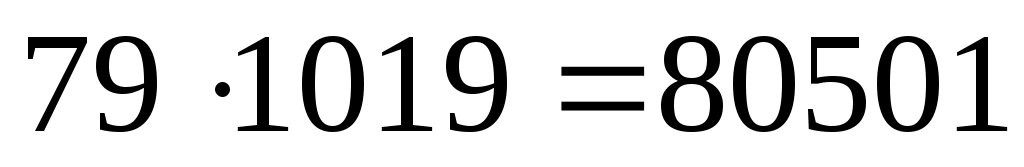 ,
,
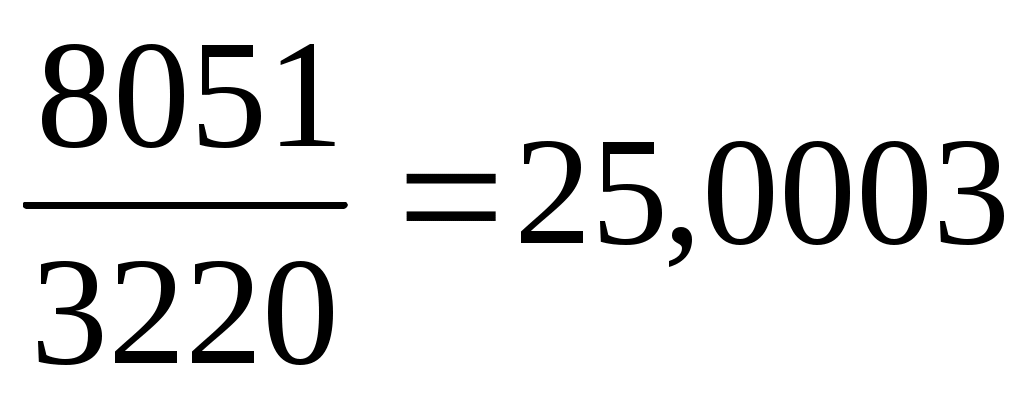
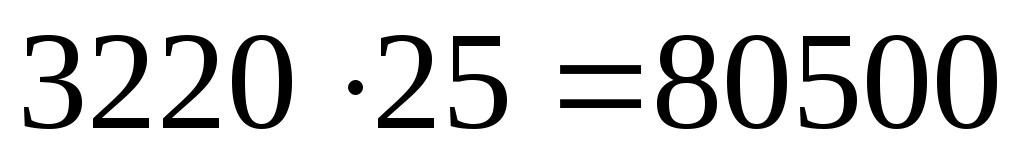
Следовательно, d=1019.
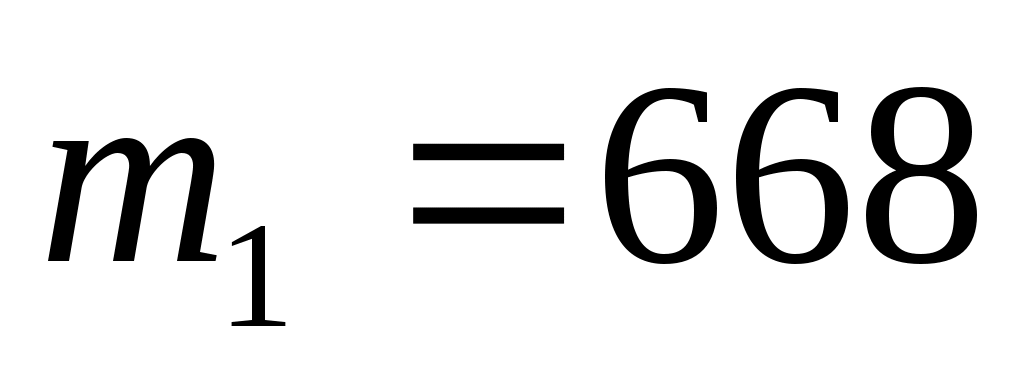 ,
, 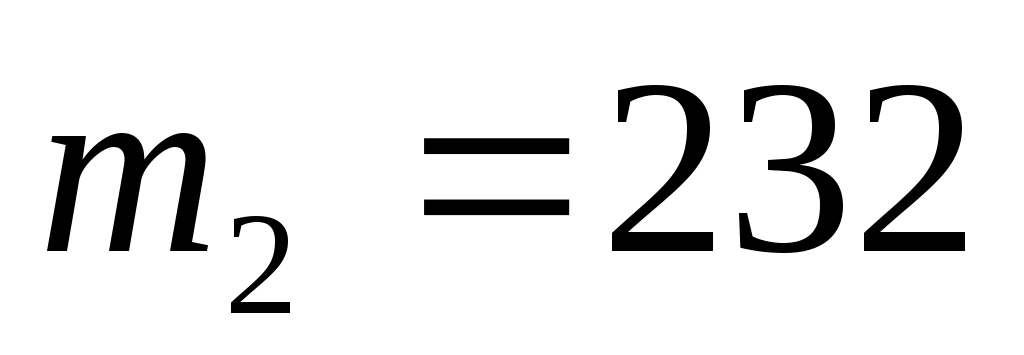 ,
, 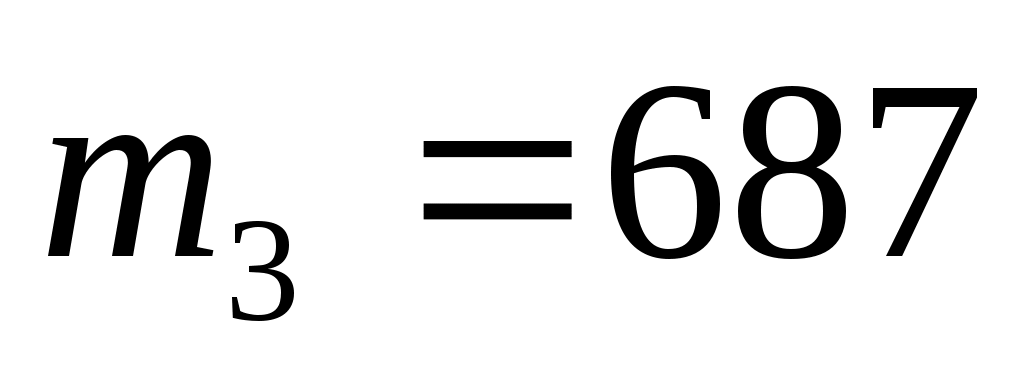 ,
, 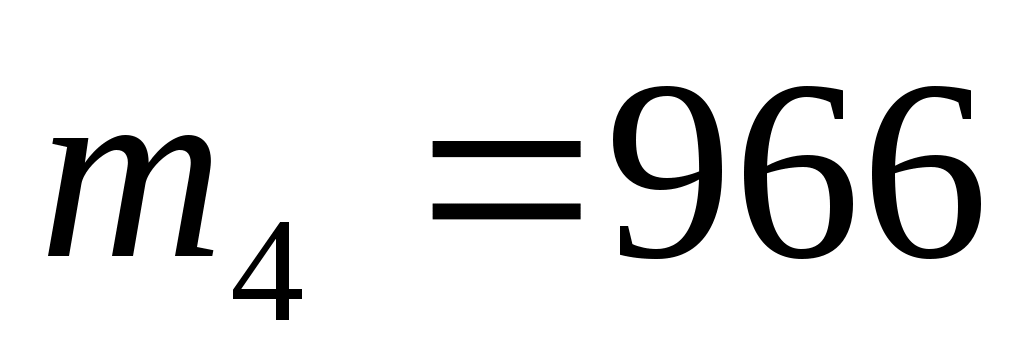 ,
, 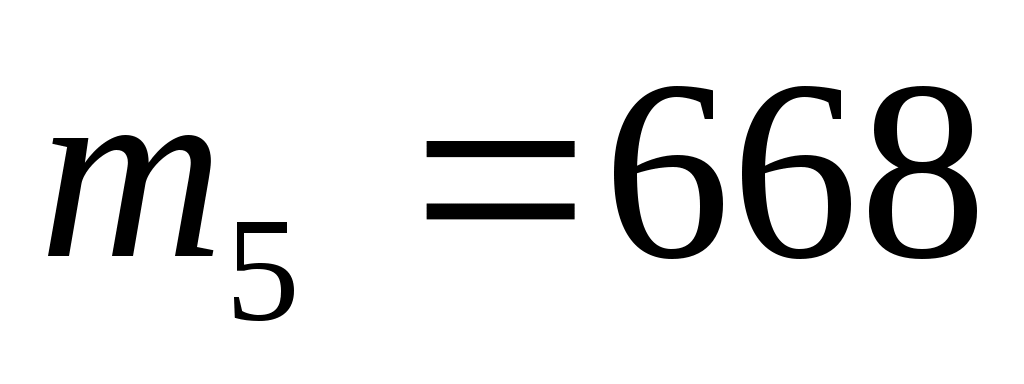 ,
, 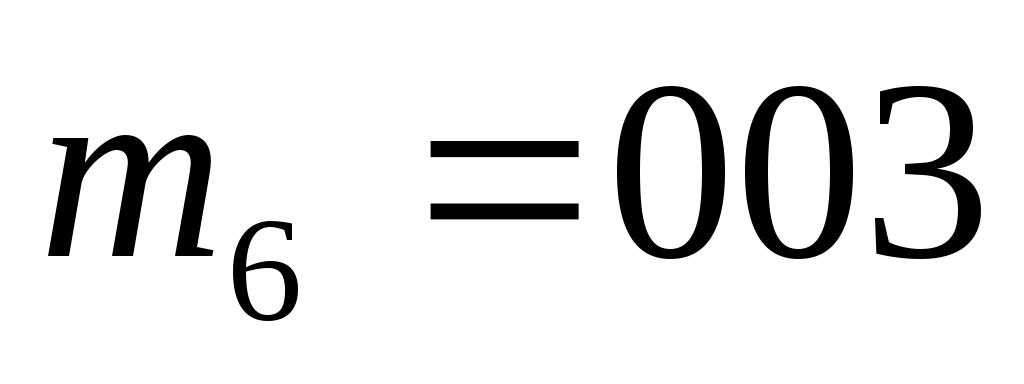
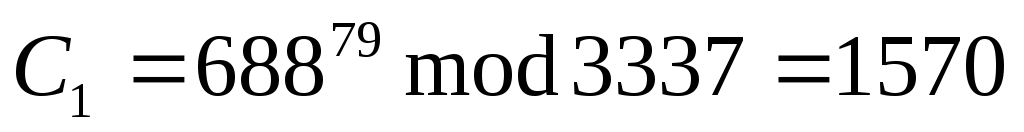 , и т.д.
, и т.д.
Получим криптограмму: С=(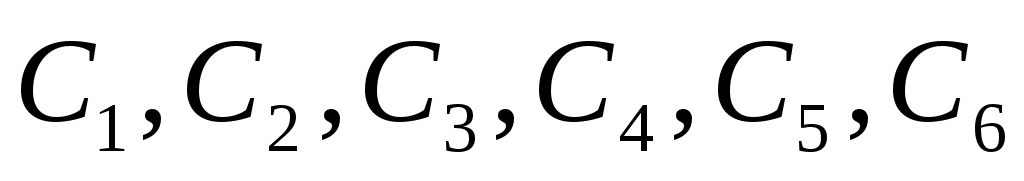 ) =
) =
=1570 2756 2091 2276 2423 0158
2756 2091 2276 2423 0158
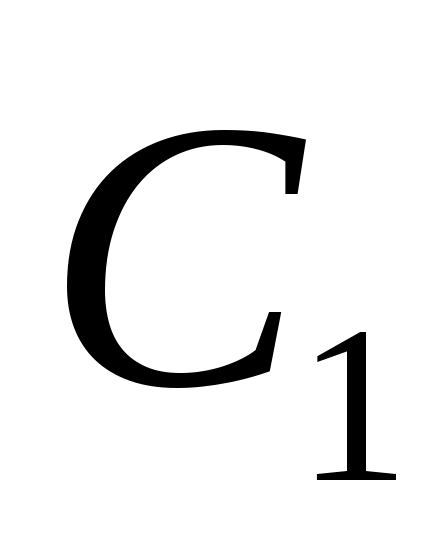

0 3
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
Ъ Э Ю К А Д Ы М О Т Е Ч С В Н Л И П Р Я Б Г Ж З Й У Ф Х Ц Ш Щ Ь
Достоинством системы Цезаря с ключевым словом является то, что количество возможных ключевых слов практически неисчерпаемо. Недостатком этой системы является возможность взлома шифртекста на основе анализа частот появления букв.
1.3.4. Шифрующие таблицы Трисемуса
В 1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием "Полиграфия". В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. При шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже неё в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самая верхнюю букву из того же столбца.
Задача 1.9. Зашифровать таблицей Трисемуса сообщение:
ВЫЛЕТАЕМ ПЯТОГО
Решение. Для русского алфавита шифрующая таблица может иметь размер 48. Шифрующая таблица выглядит так:
| Б | А | Н | Д | Е | Р | О | Л |
| Ь | В | Г | Ж | З | И | Й | К |
| М | П | С | Т | У | Ф | Х | Ц |
| Ч | Ш | Щ | Ы | Ъ | Э | Ю | Я |
Рисунок 1.5 - Шифрующая таблица Трисемуса с ключевым словом БАНДЕРОЛЬ
Используя эту таблицу в соответствии с вышеизложенной методикой
, получаем шифртекст
ПДКЗЫВЗЧШЛЫЙСЙ.
Такие табличные шифры называются монограммными, так как шифрование выполняется по одной букве. Трисемус первым заметил, что шифрующие таблицы позволяют шифровать сразу по две буквы. Такие шифры называются биграммными.
1.3.5. Биграммный шифр Плейфейра
Шифр Плейфейра, изобретенный в 1854 г., является наиболее известным биграммным шифром замены. Он применялся Великобританией во время первой мировой войны. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.
Для удобства запоминания шифрующей таблицы отправителем и получателем сообщений можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей таблицей Трисемуса из предыдущей задачи ( рис. 1.5).
Процедура шифрования включает следующие шаги.
-
Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.
-
Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
2а.Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы А и Й в табл. на рис.2.6), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это – буквы АЙОВ. Пара букв АЙ отображается в пару ОВ. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста.)
2б.Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в.Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.)
Задача 1.10. Зашифровать биграммным шифром Плейфера текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Решение.Разобьём этот текст на биграммы:
ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы (рис. 1.5) в следующую последовательность биграмм шифртекста
ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ
При дешифровании применяется обратный порядок действий.
Шифрование биграммами резко повышает стойкость шифров к вскрытию. Хотя книга И.Трисемуса "Полиграфия" была относительно доступной, описанные в ней идеи получили признание лишь спустя три столетия. По всей вероятности, это было обусловлено плохой осведомленностью криптографов о работах богослова и библиофила Трисемуса в области криптографии.
Пояснение к заданию 2
Методы шифрования
2.1. Метод перестановок на основе маршрутов
Гамильтона
Этот метод реализуется путем выполнения следующих шагов.
Шаг 1. Исходный текст разбивается на блоки. Если длина шифруемого текста не кратна длине блока, то на свободные места последнего блока помещаются служебные символы-заполнители(например,*)
Шаг 2. Символами блока заполняется таблица, в которой для каждого порядкового номера символа в блоке отводится вполне определенное место (рис. 2.1).
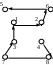
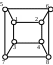
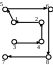
Исходная
таблица
Маршрут 1
Маршрут 2
Рисунок 2.1 - Вариант 8-элементной таблицы и маршрутов
Гамильтона.
Шаг 3. Считывание символов из таблицы осуществляется по одному из маршрутов. Увеличение числа маршрутов повышает криптостойкость шифра. Маршруты выбирают либо последовательно, либо их очерёдность задаётся ключом К.
Шаг 4. Зашифрованная последовательность символов разбивается на блоки фиксированной длины L. Величина L может отличаться от длины блоков, на которые разбивается исходный текст на шаге 1.
Расшифрование производится в обратном порядке.
Задача 2.1. Требуется зашифровать текст 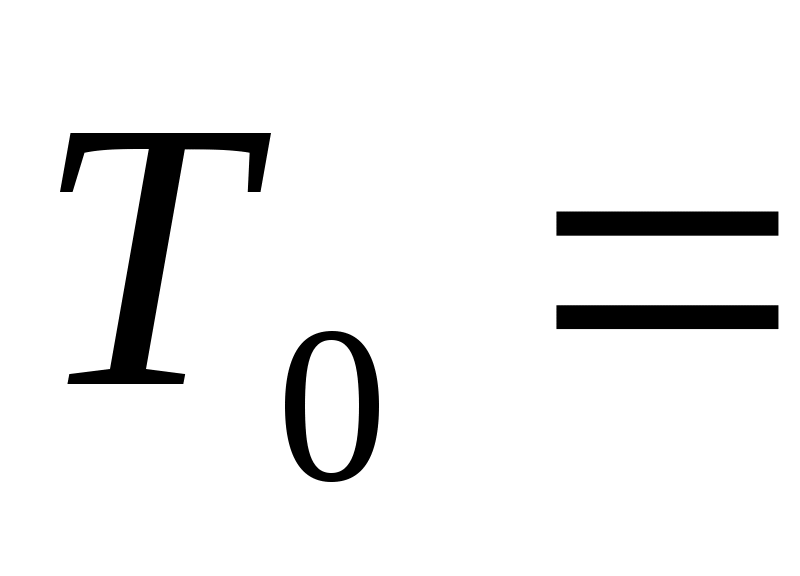 <МЕТОДЫ ПЕРЕСТАНОВКИ>. Ключ и длины зашифрованных блоков равны: К=<2,1,1>, L=4. Для шифрования использовать таблицу и два маршрута, представленные на рис.2.1.
<МЕТОДЫ ПЕРЕСТАНОВКИ>. Ключ и длины зашифрованных блоков равны: К=<2,1,1>, L=4. Для шифрования использовать таблицу и два маршрута, представленные на рис.2.1.
Решение. Воспользуемся вышеизложенной методикой построения шифра по шагам.
Шаг 1. Исходный текст разбивается на 3 блока:
Блок 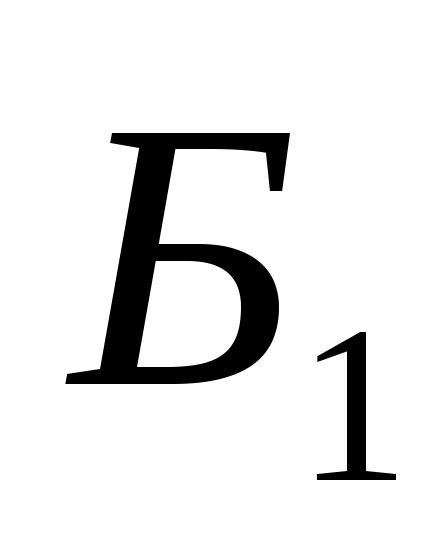 =<МЕТОДЫ П>
=<МЕТОДЫ П>
Блок 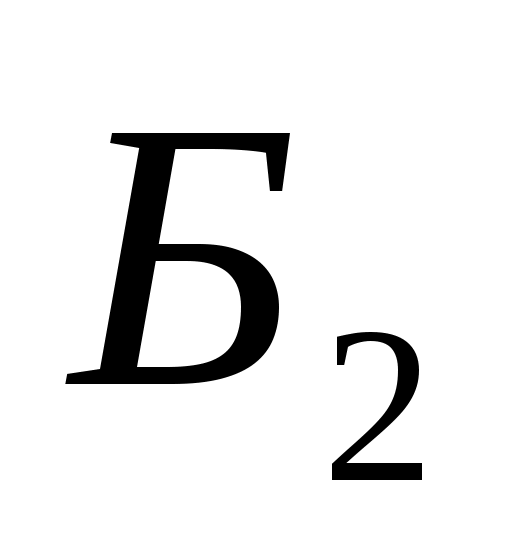 =<ЕРЕС ТАНО>
=<ЕРЕС ТАНО>
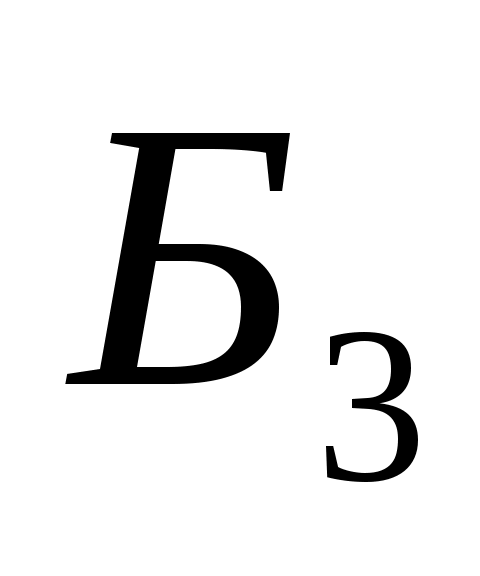 =<ВКИ*****>
=<ВКИ*****>
Шаг 2. Заполняется 3 матрицы с маршрутами 2,1,1 (рис.2.2.)
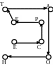
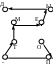
Маршрут 2
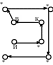
Маршрут 1
Маршрут 1
Рисунок 2.2 - Шифрование с помощью маршрутов Гамильтона.
Шаг 3. Получение шифртекста путём расстановки символов в соответствии с маршрутами.
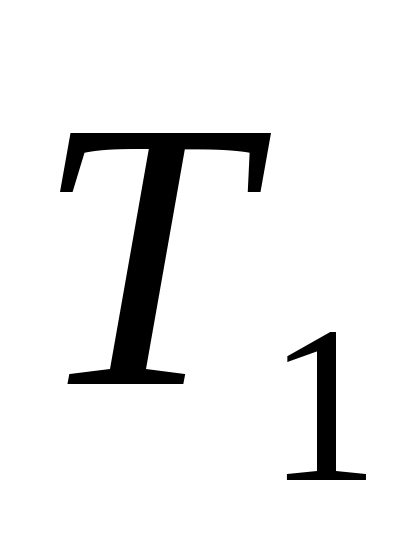 =<ОП_ТМЕЫДЕСРЕТАОНИ*КВ****>
=<ОП_ТМЕЫДЕСРЕТАОНИ*КВ****>
Шаг4. Разбиение на блоки шифртекста
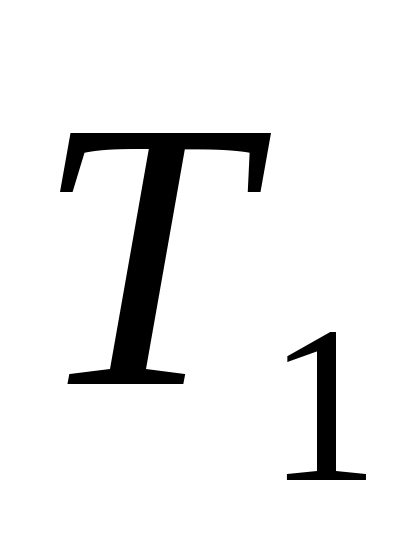 =<ОП_Т МЕЫД ЕСРЕ ТАОН И*КВ ****>
=<ОП_Т МЕЫД ЕСРЕ ТАОН И*КВ ****>
Возможно применение и других маршрутов.
2.2. Аналитические методы шифрования
Среди аналитических методов наибольшее распространение получили методы, основанные на использовании матриц. Зашифрование К-го блока исходной информации, представленного в виде вектора 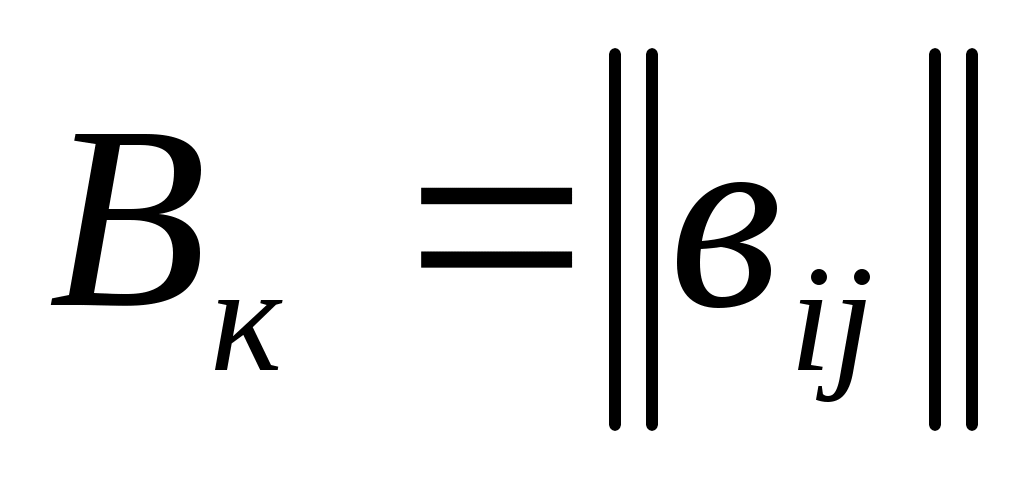 осуществляется путём перемножения матрицы ключа
осуществляется путём перемножения матрицы ключа 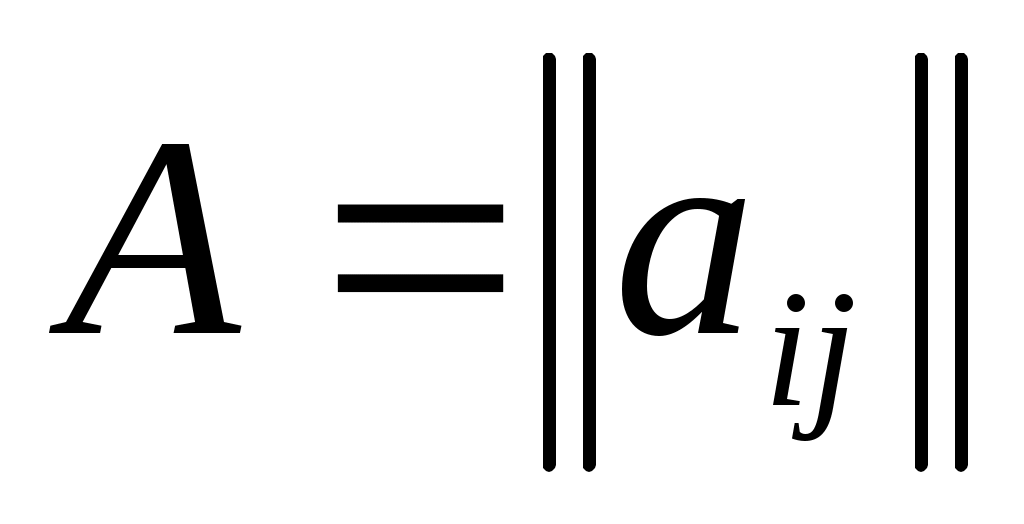 и вектора
и вектора 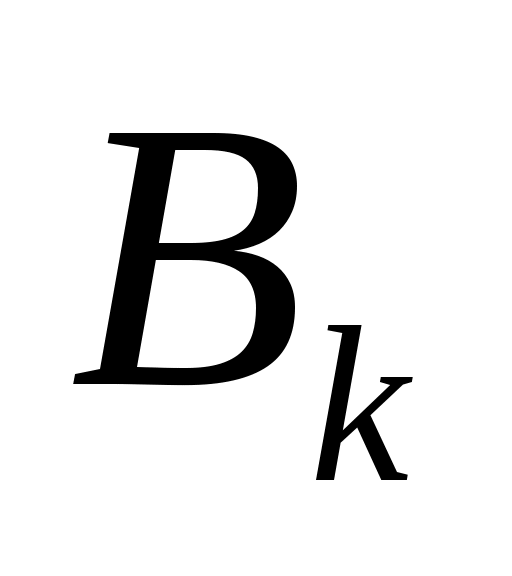 . В результате перемножения получается блок шифртекста в виде вектора
. В результате перемножения получается блок шифртекста в виде вектора 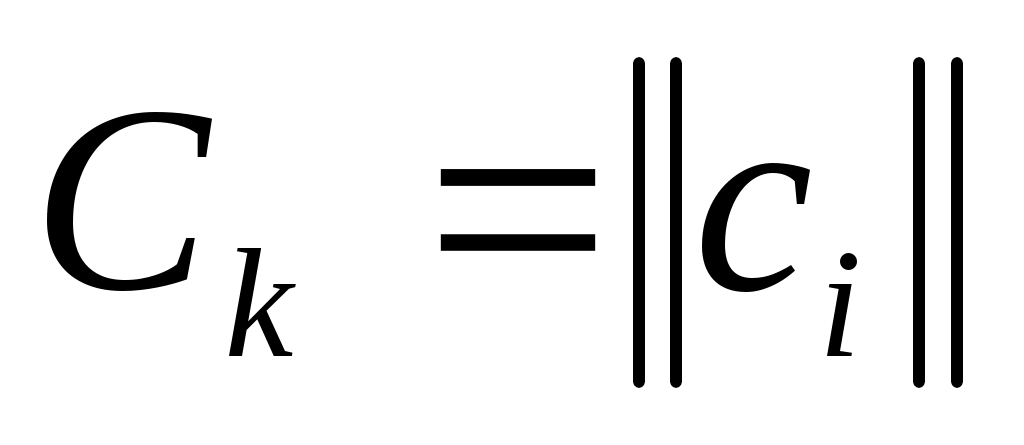 , где элементы вектора
, где элементы вектора 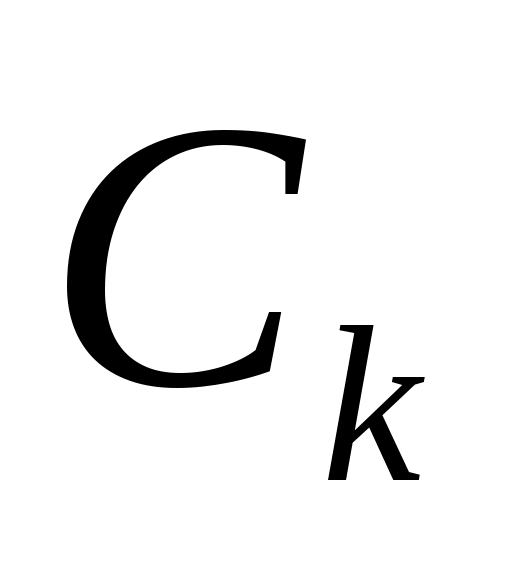 определяются по формуле:
определяются по формуле:
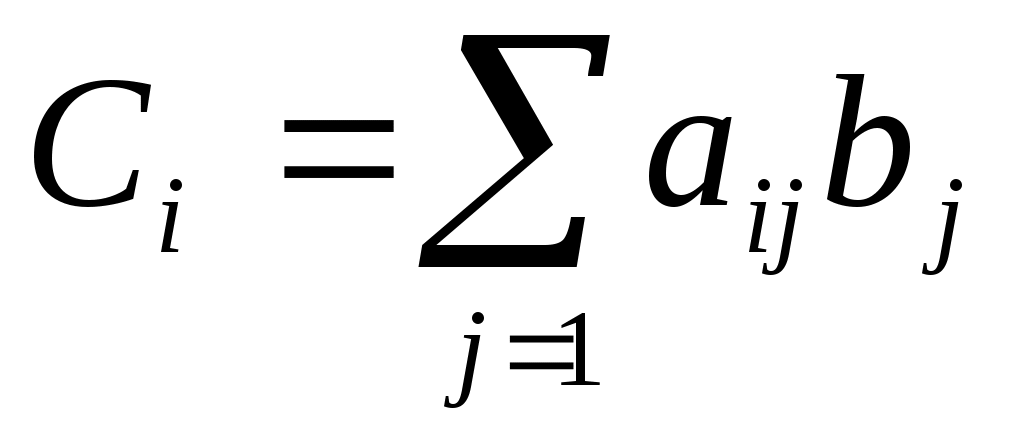 .
.
Расшифрование информации осуществляется путём последовательного перемножения векторов 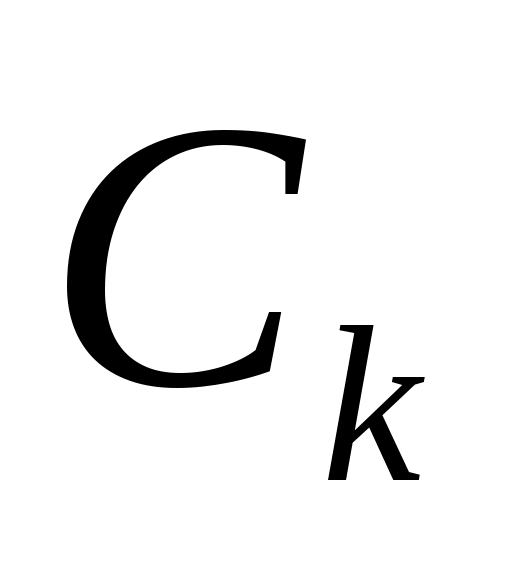 и обратной матрицы
и обратной матрицы 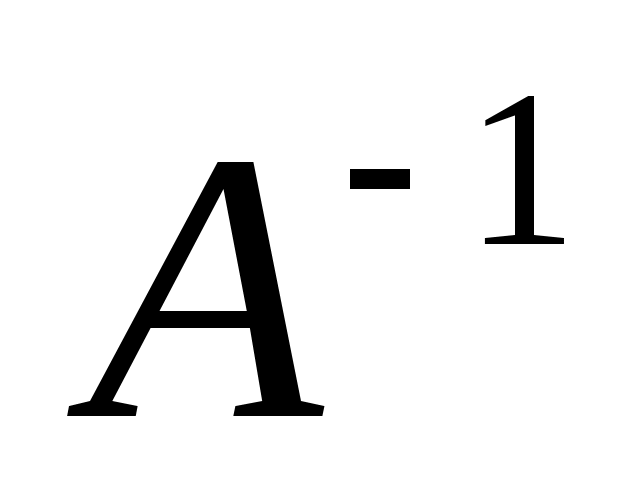 .
.
Задача 2.2. Требуется зашифровать слово 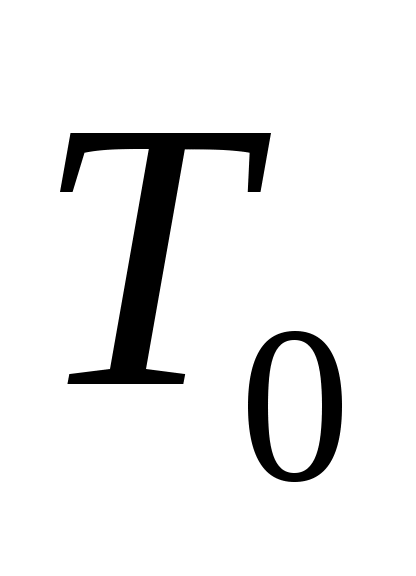 =<ЗАБАВА> с помощью матрицы-ключа А.
=<ЗАБАВА> с помощью матрицы-ключа А.
A=


Решение.
1.Определим числовой эквивалент исходного слова как последовательность соответствующих порядковых номеров букв слова 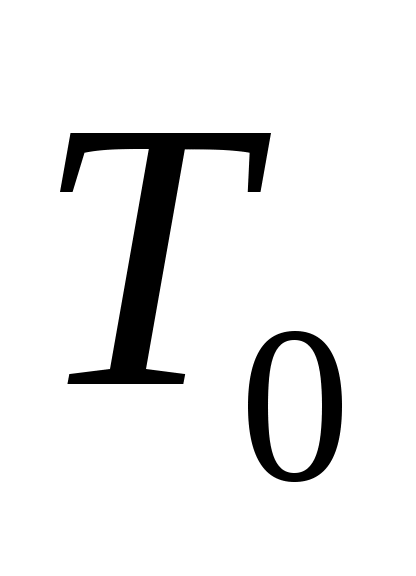 :
:
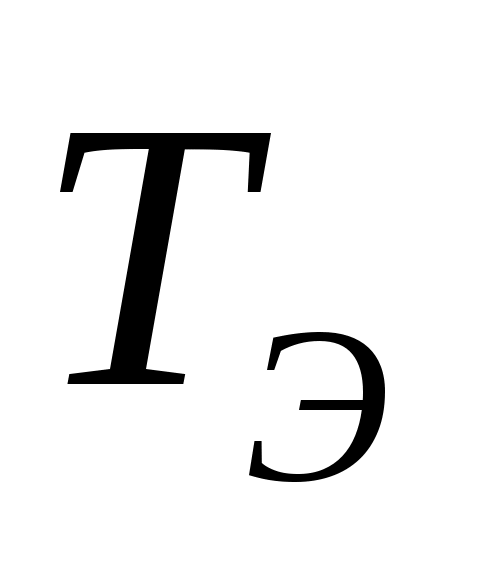 =<8,1,2,1,3,1>
=<8,1,2,1,3,1>
2.Разобьём 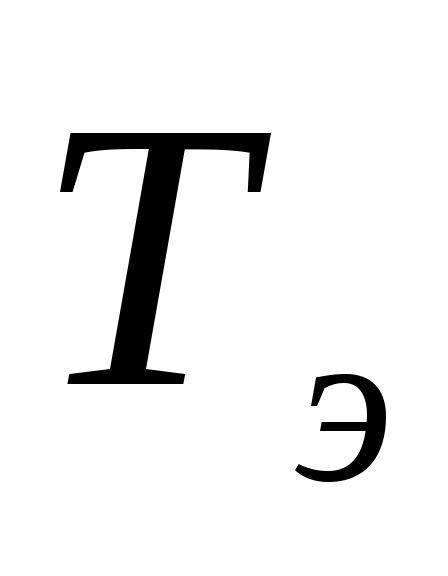 на два вектора
на два вектора 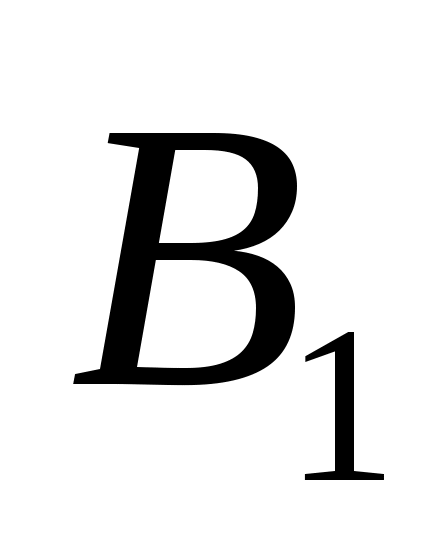
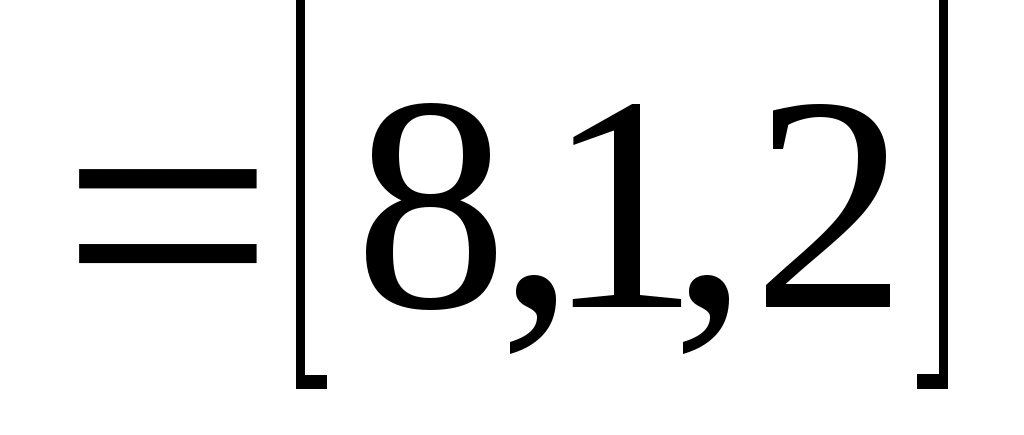 и
и 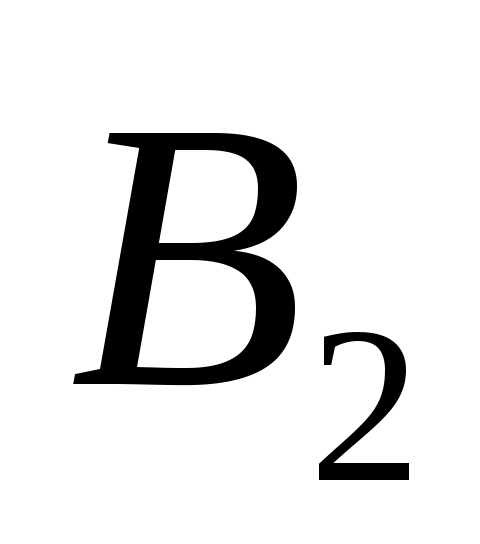
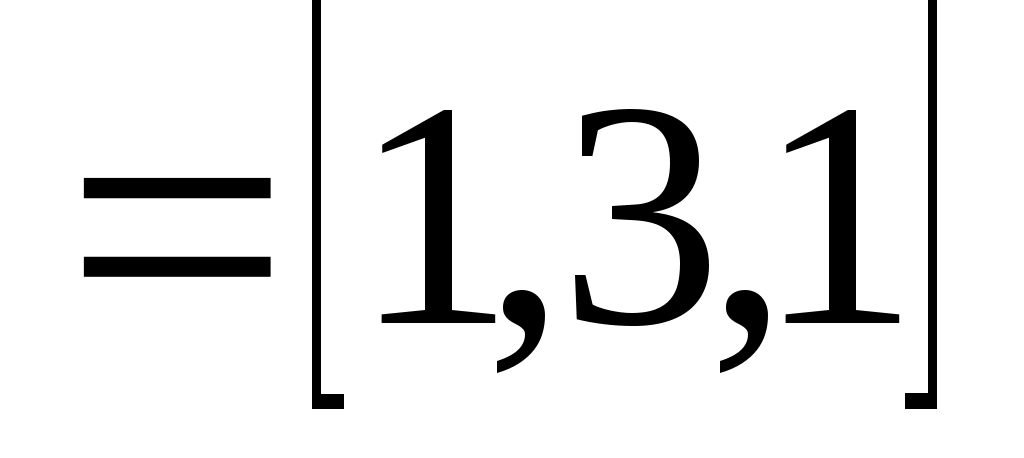
3. Умножим матрицу А на векторы 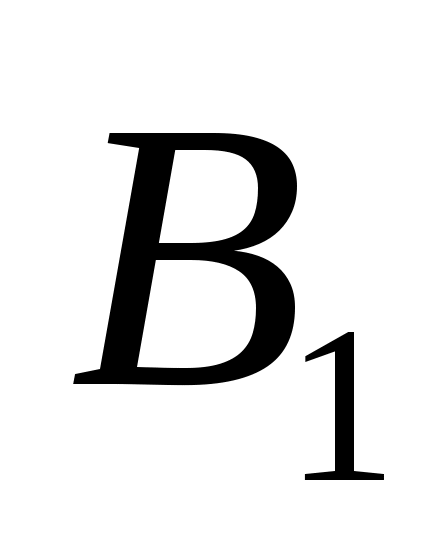 и
и 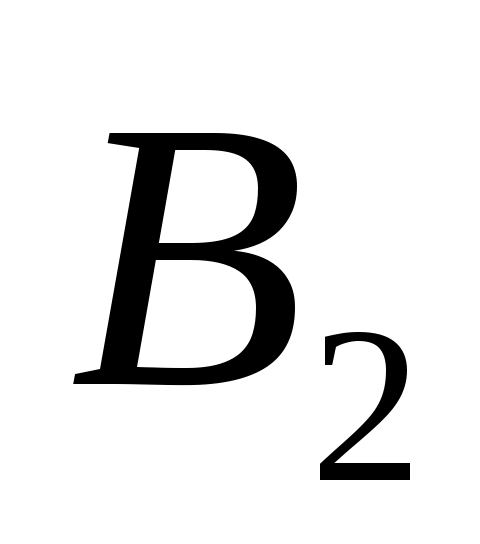 :
:
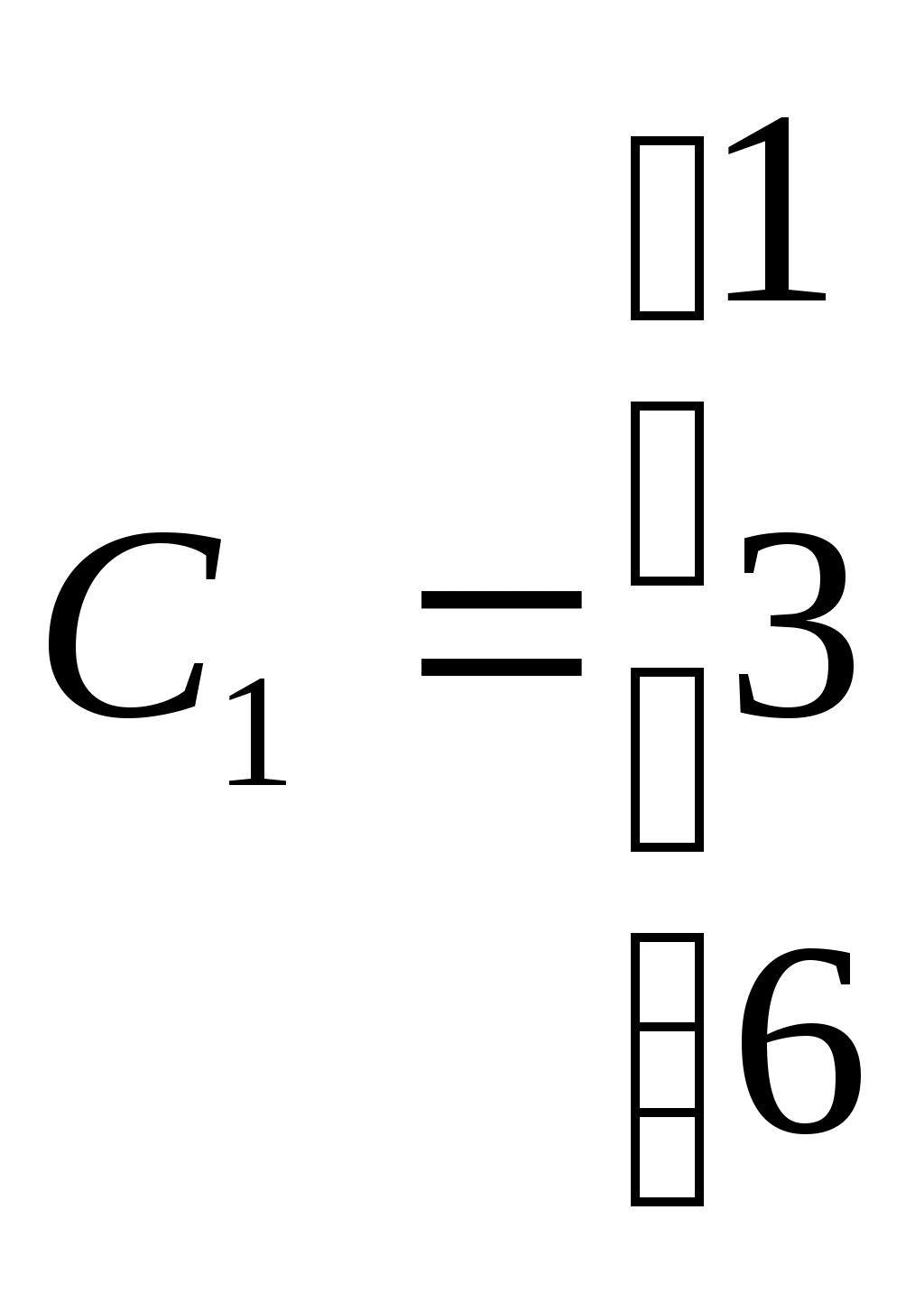


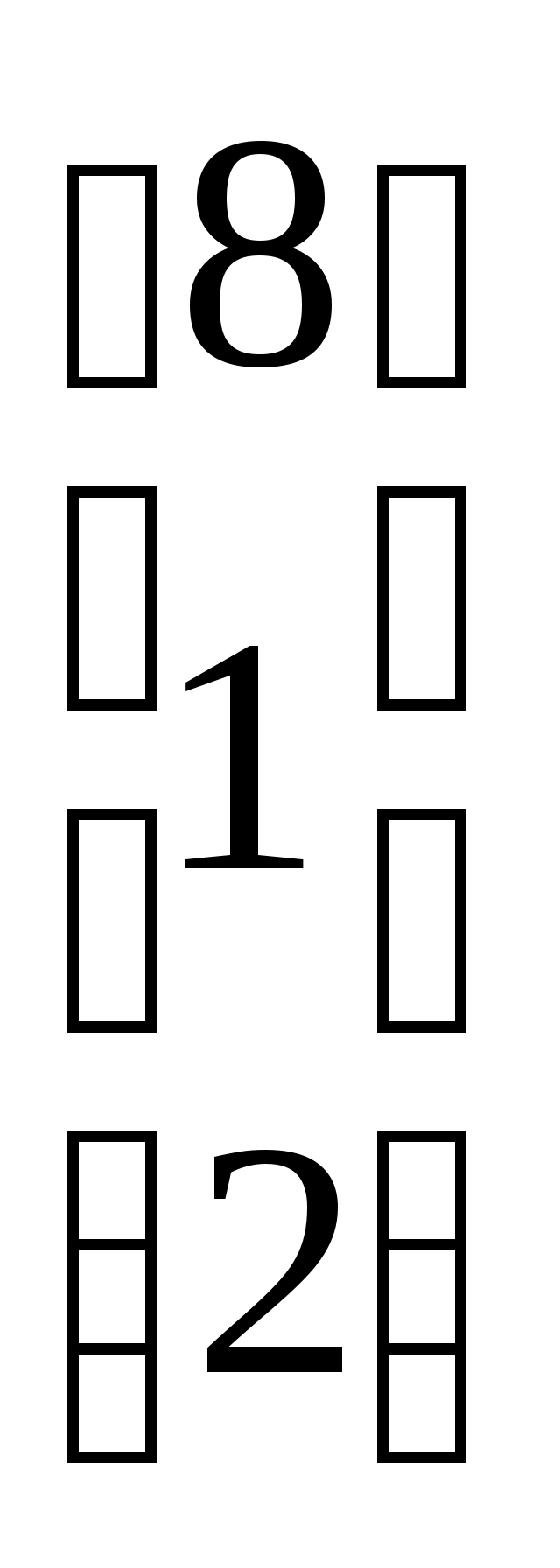 =
= 
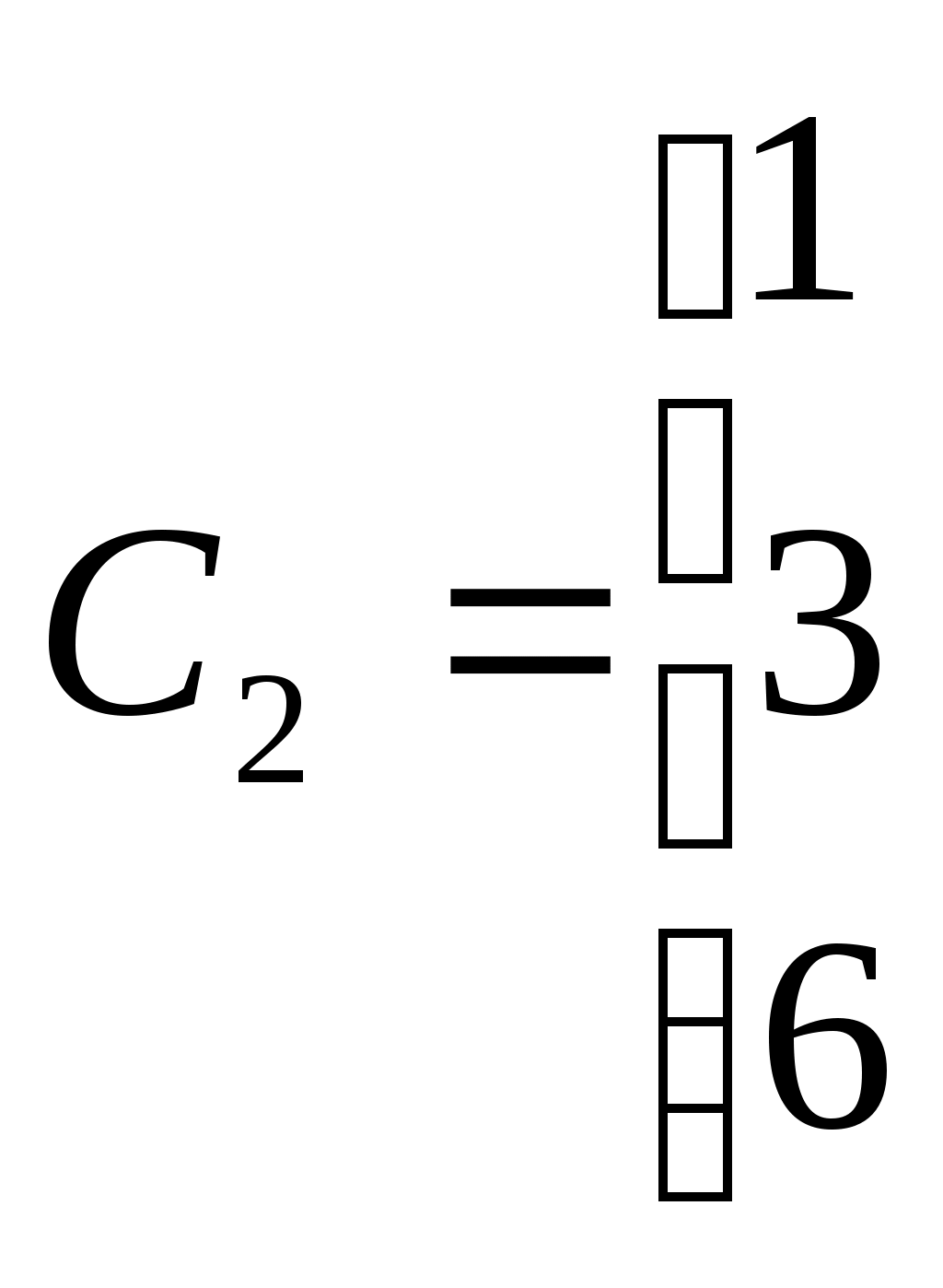


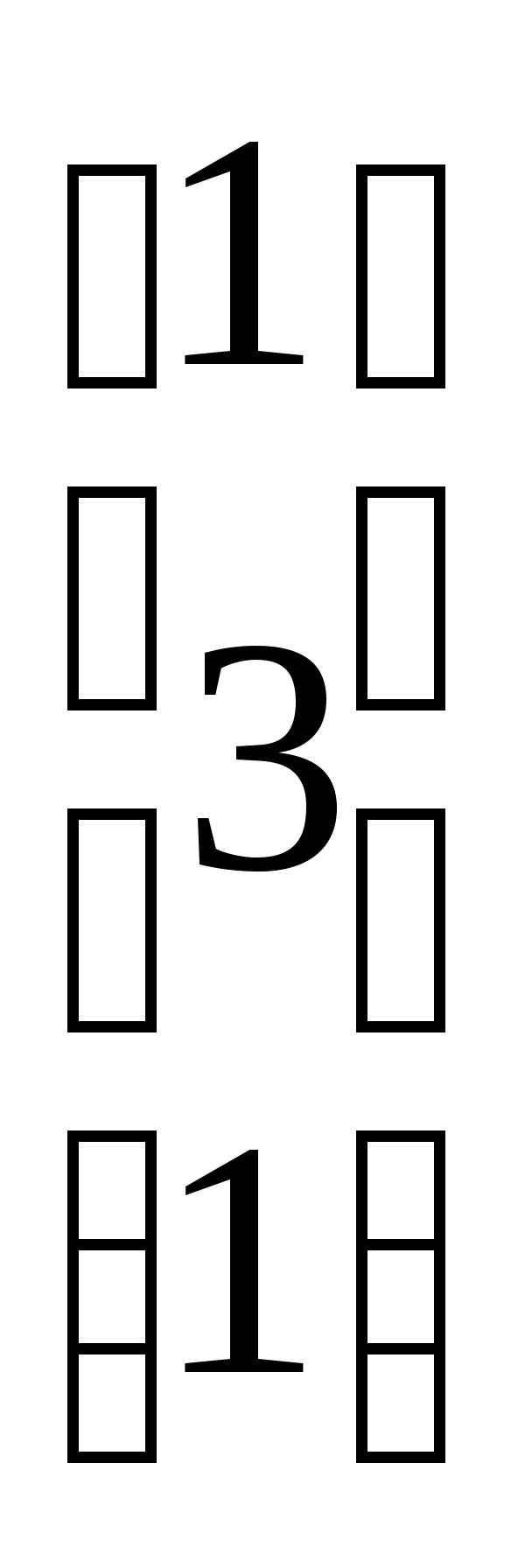 =
= 
4. Зашифрованное слово запишем в виде последовательности чисел 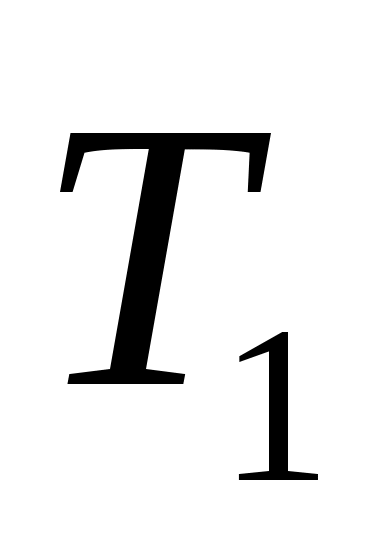 =<28,35,67,21,26,38>.
=<28,35,67,21,26,38>.
Задача 2.3. Расшифровать текст, полученный в задаче 2.2.
Решение.
1.Вычисляется определитель 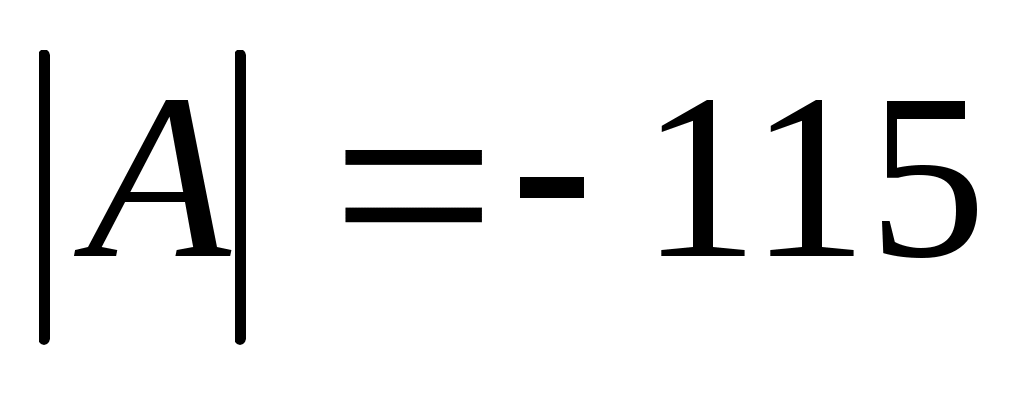 .
.
2.Определяется присоединённая матрица  , каждый элемент которой является алгебраическим дополнением элемента
, каждый элемент которой является алгебраическим дополнением элемента  матрицы А:
матрицы А:
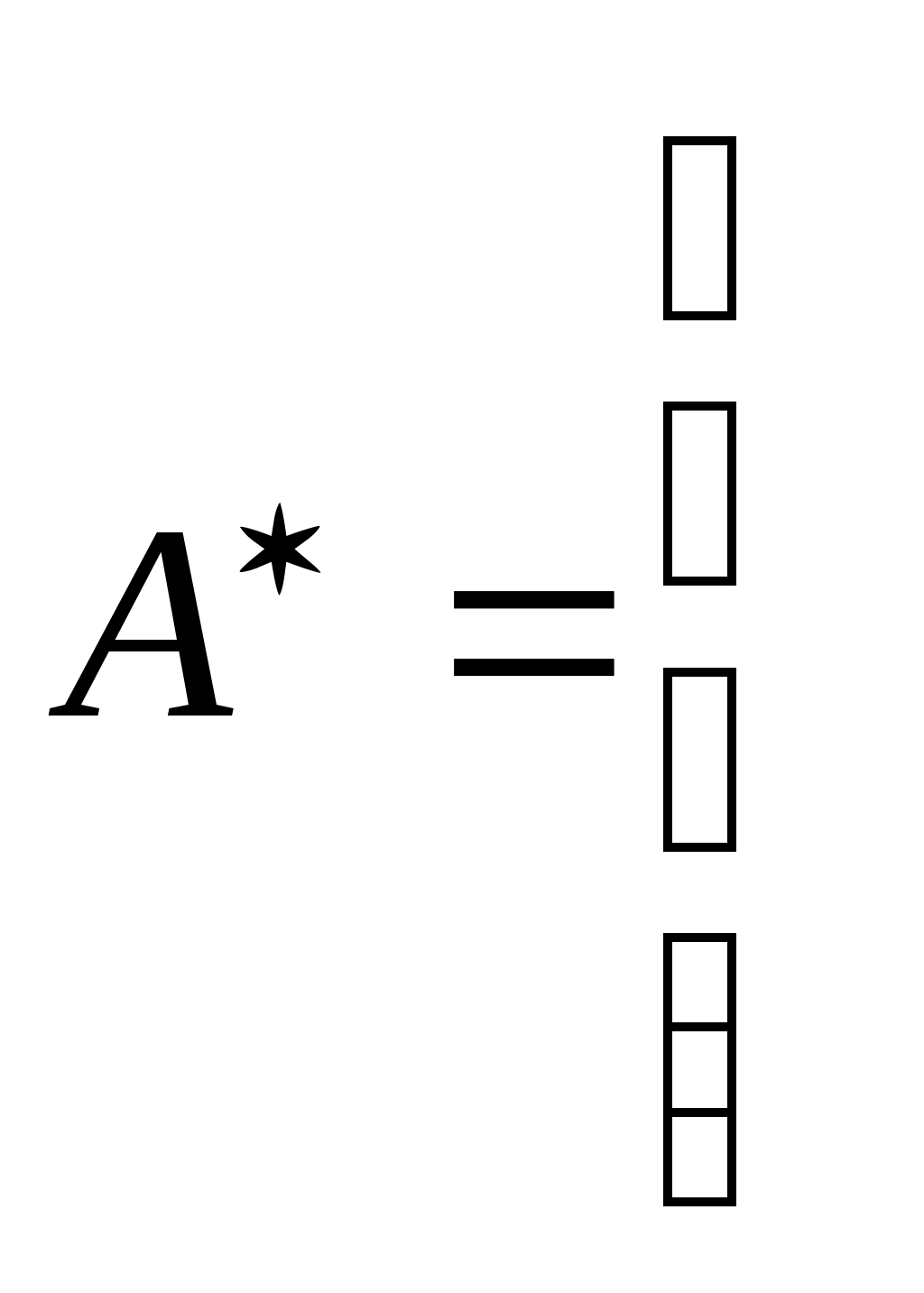
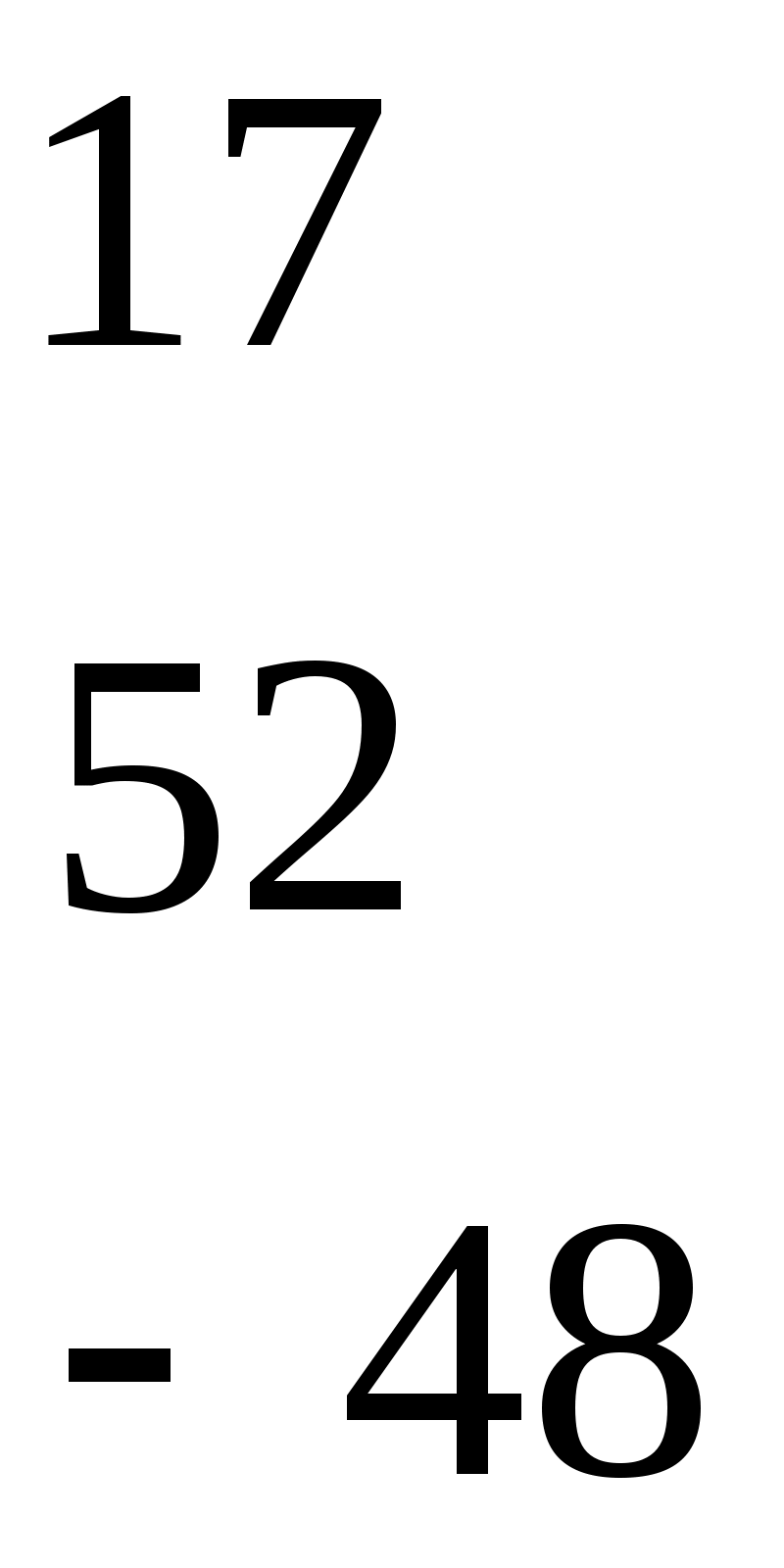
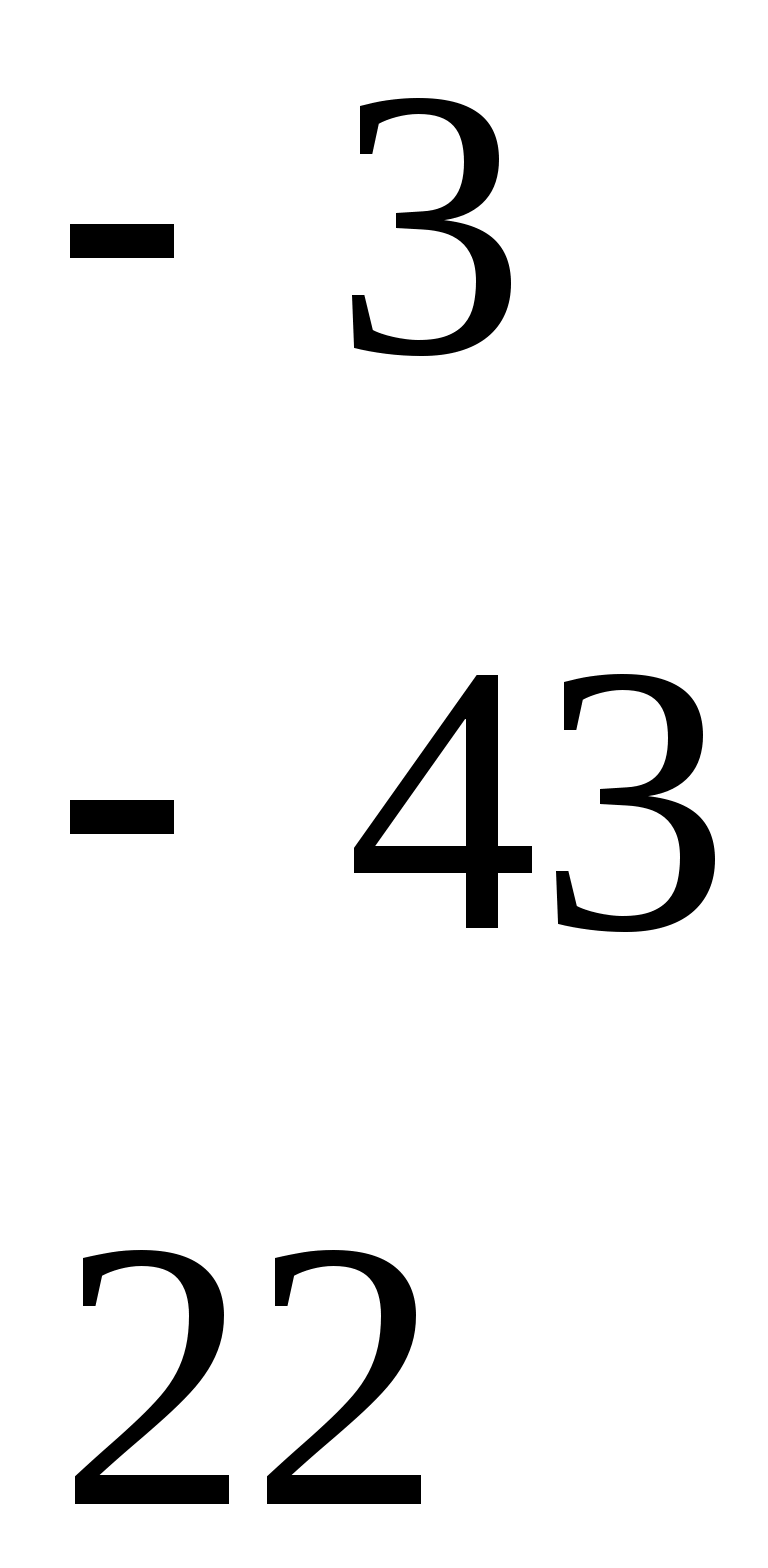
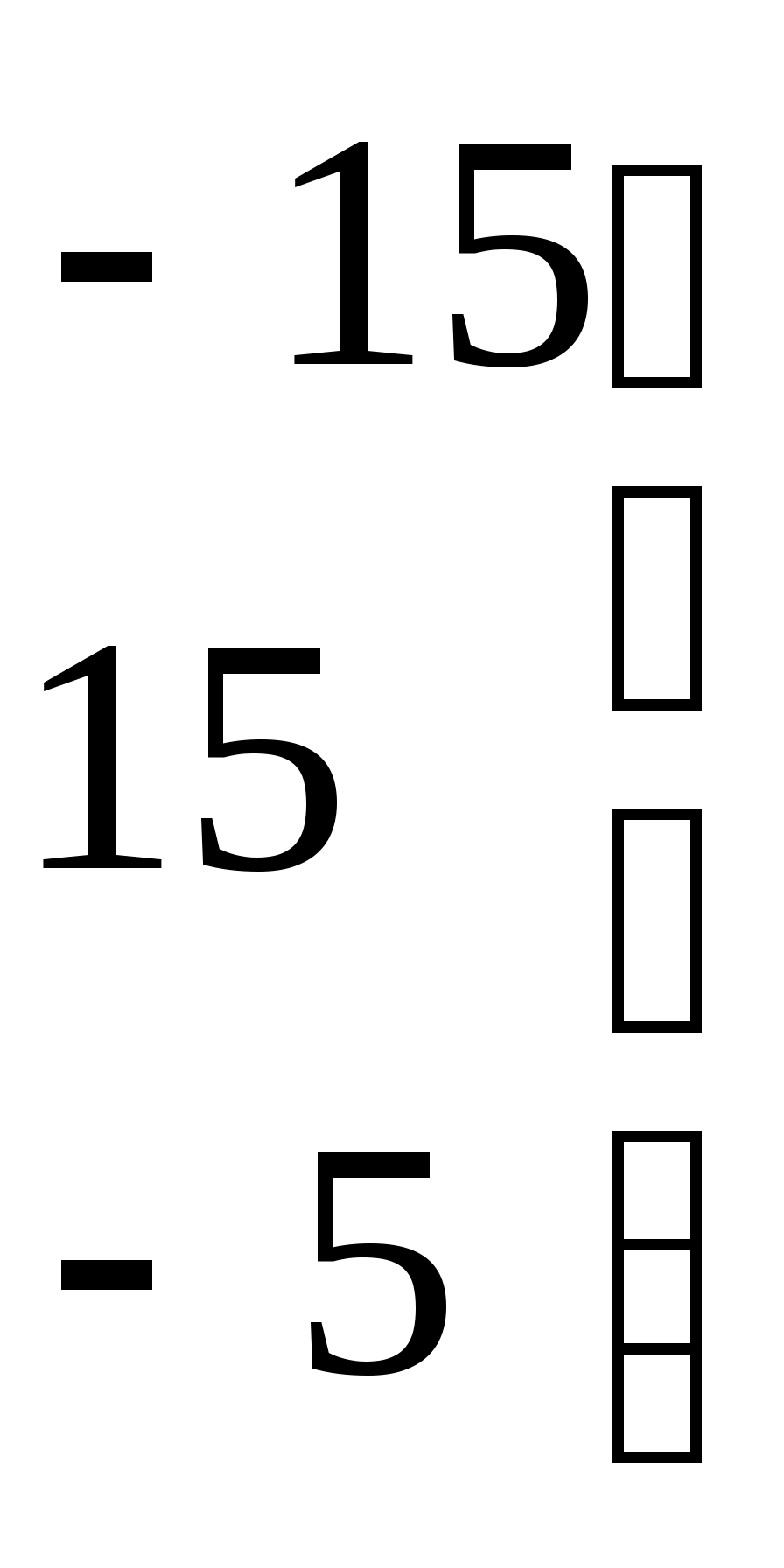
3.Получается транспонированная матрица 
 =
=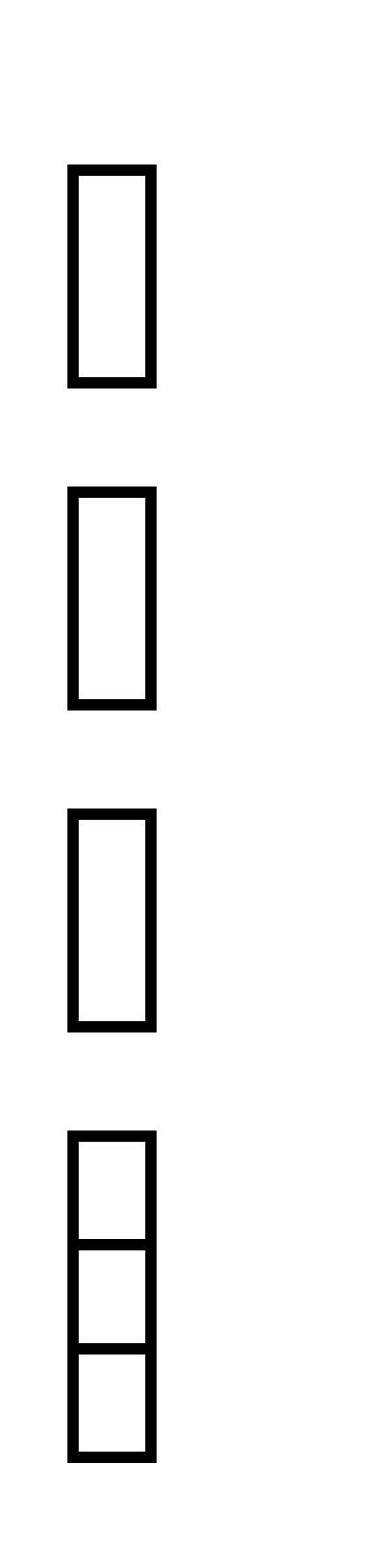
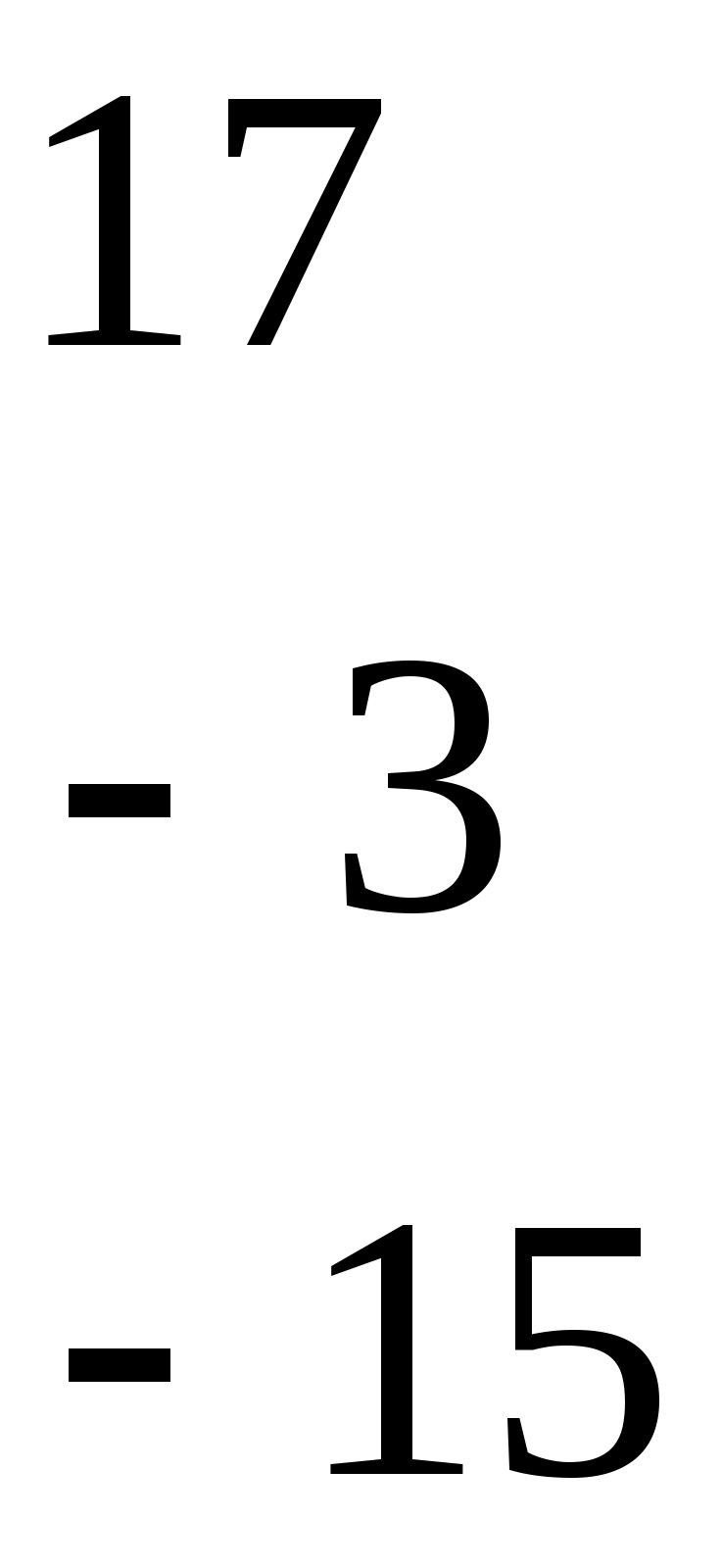
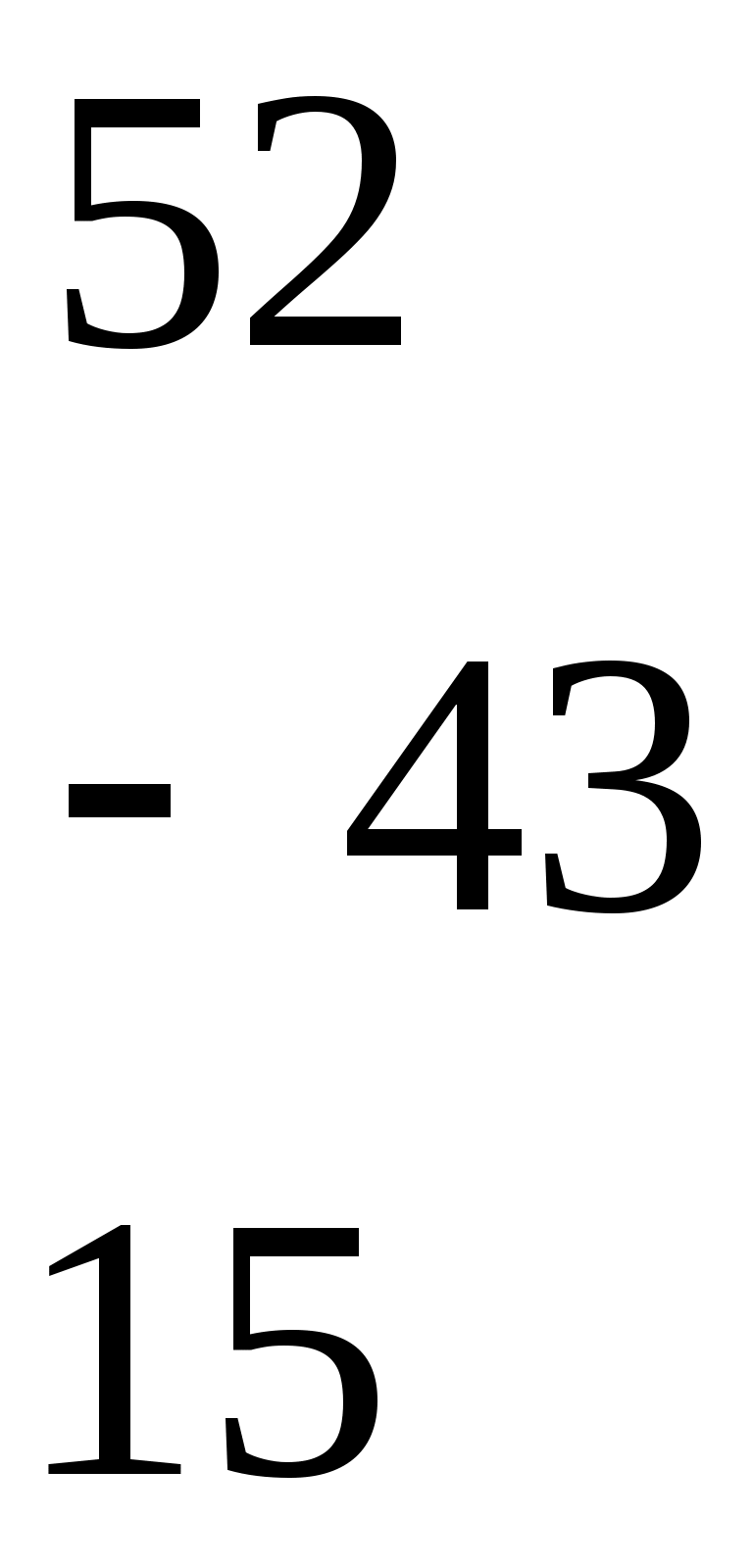
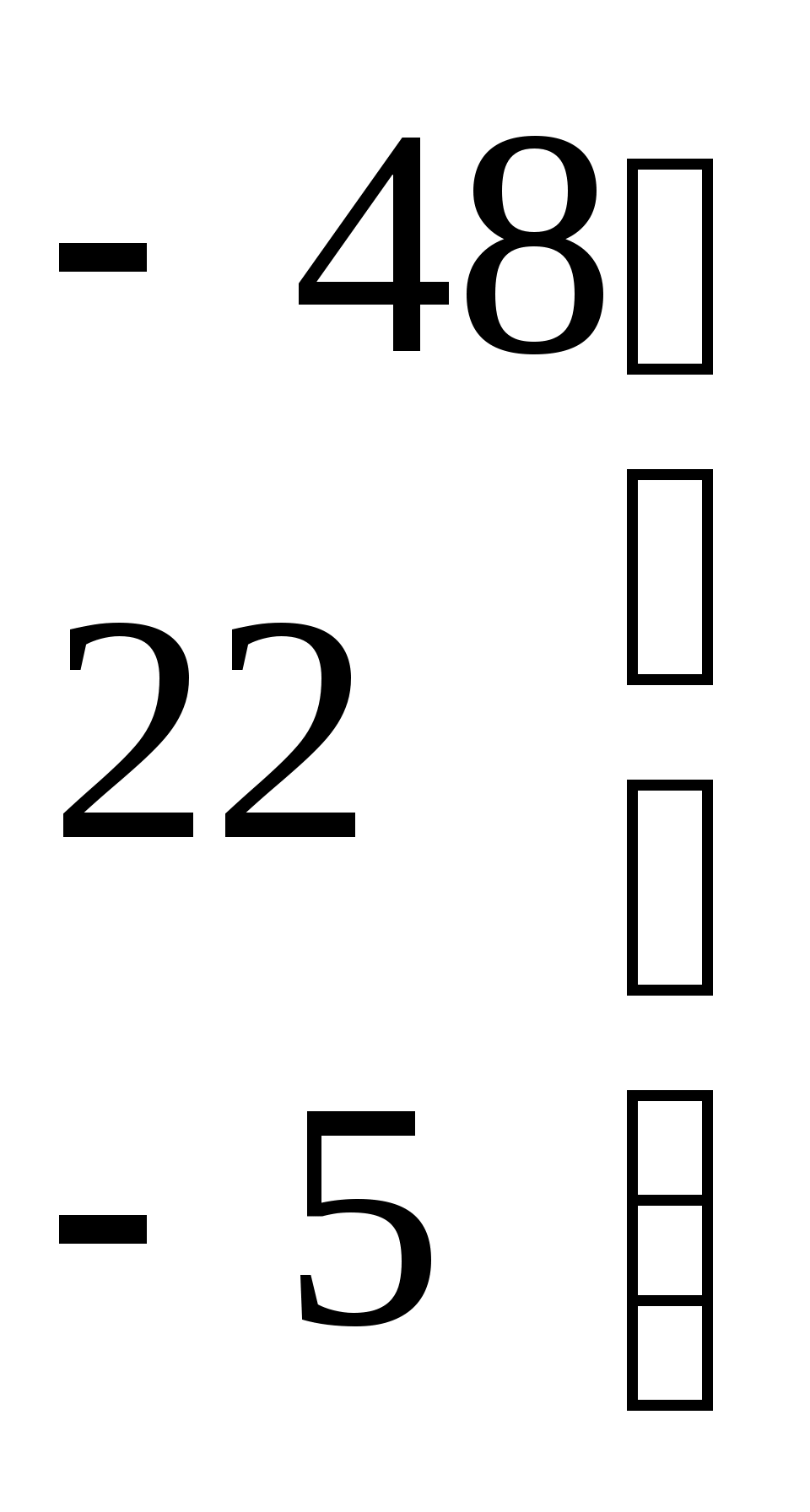
4.Вычисляется обратная матрица 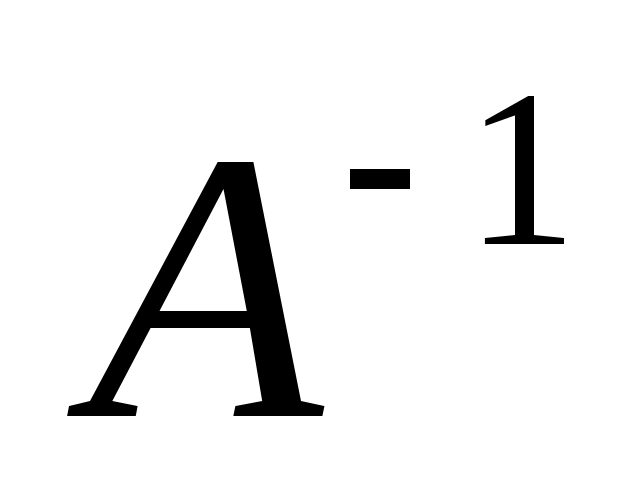 по формуле:
по формуле:
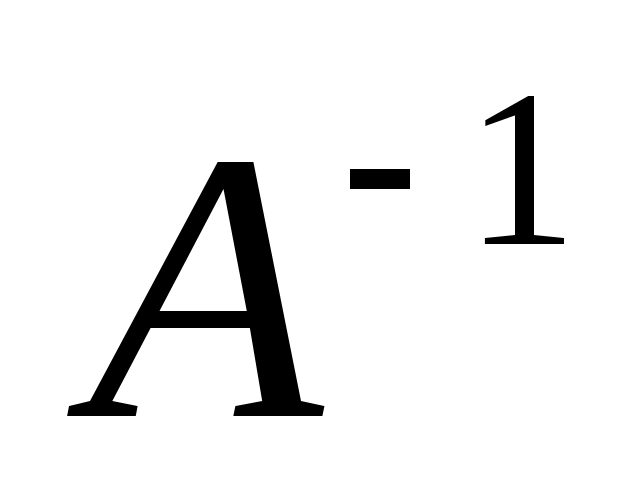 =
= ,
,
В результате вычислений обратная матрица имеет вид:
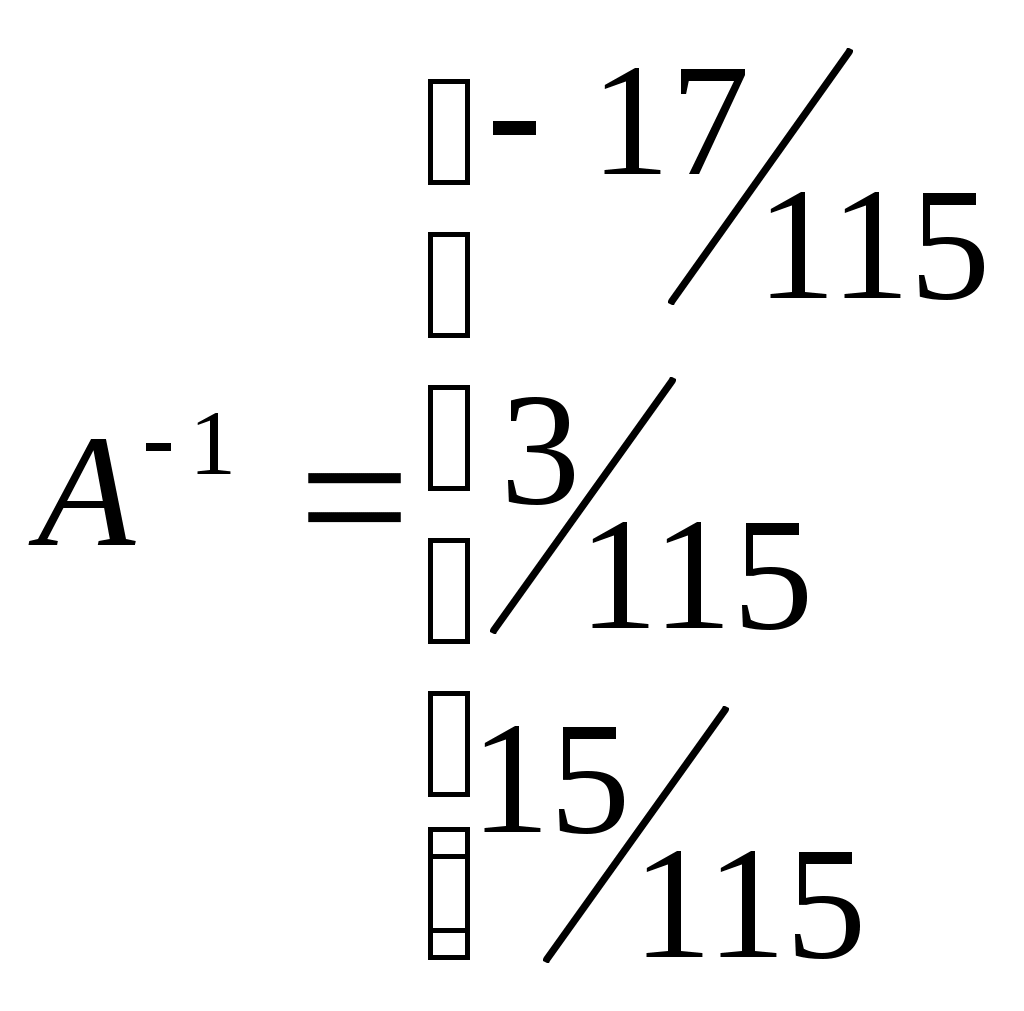
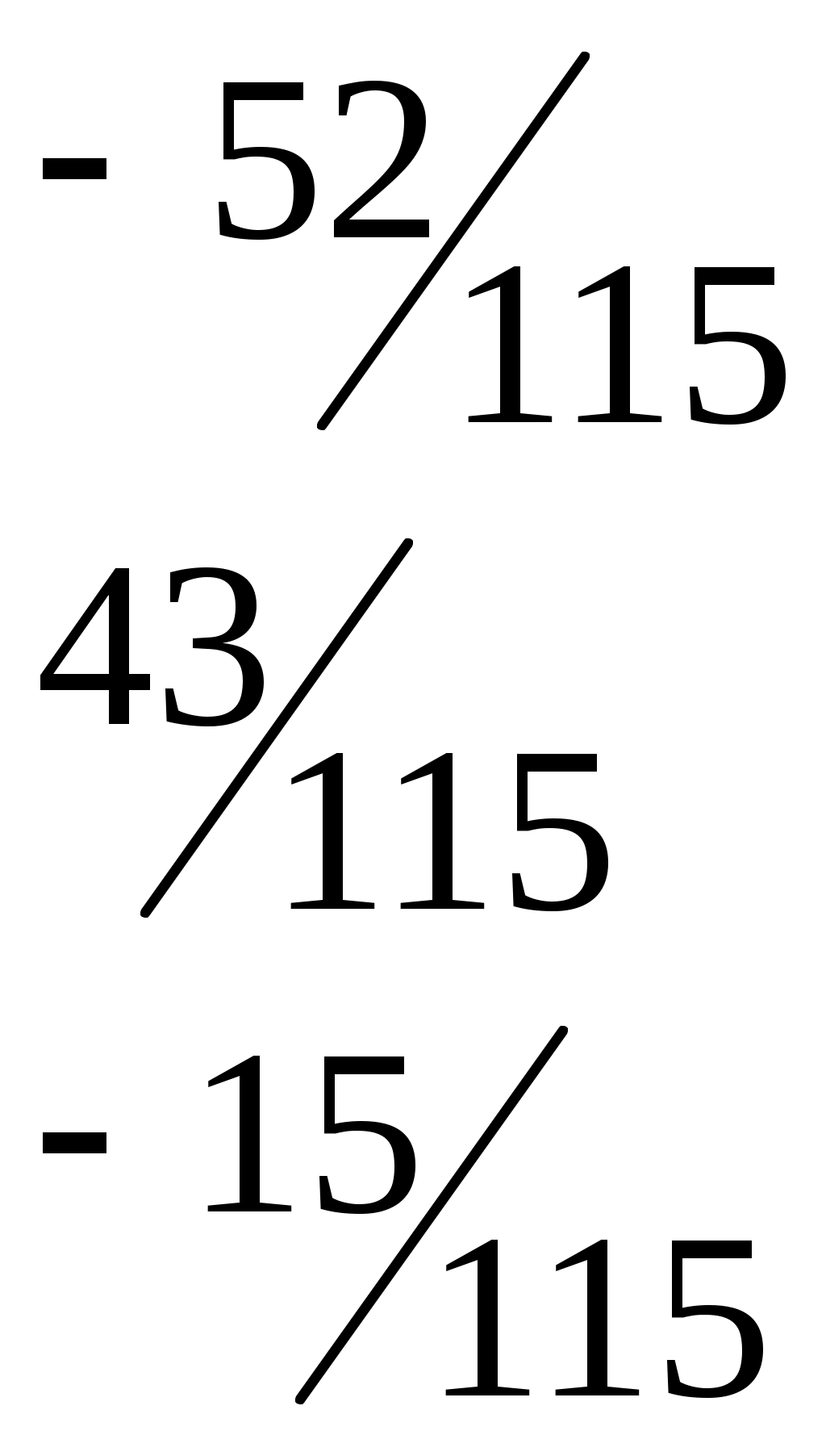
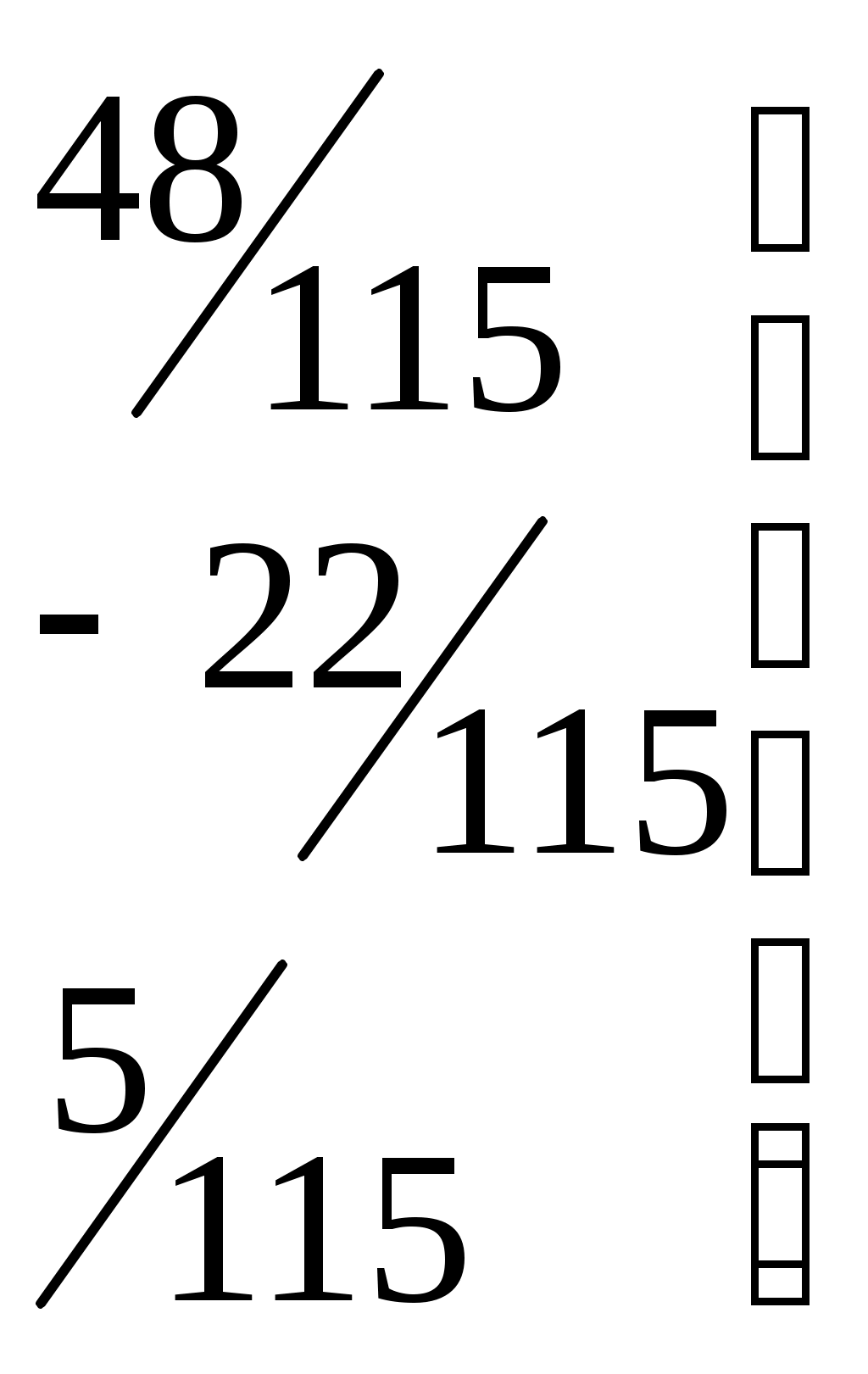
5.Определяются векторы 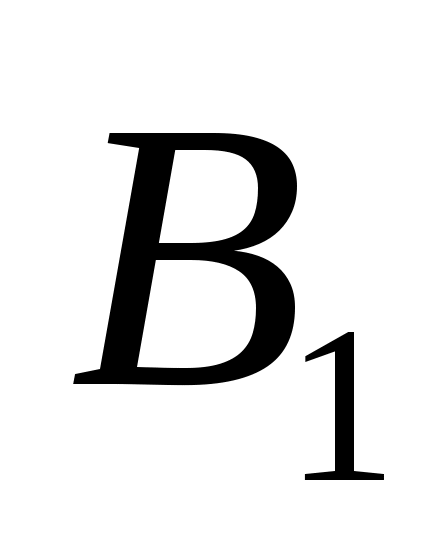 и
и 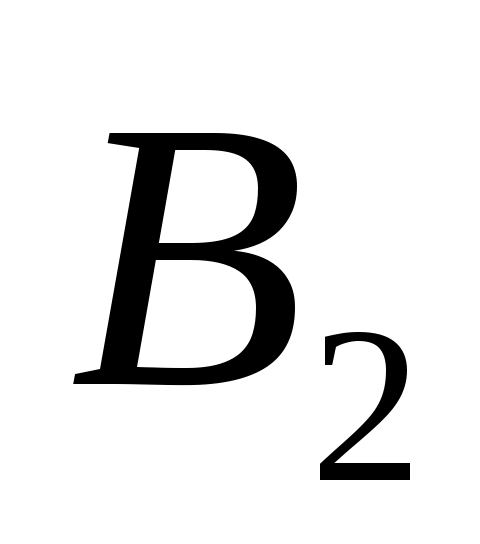 :
:
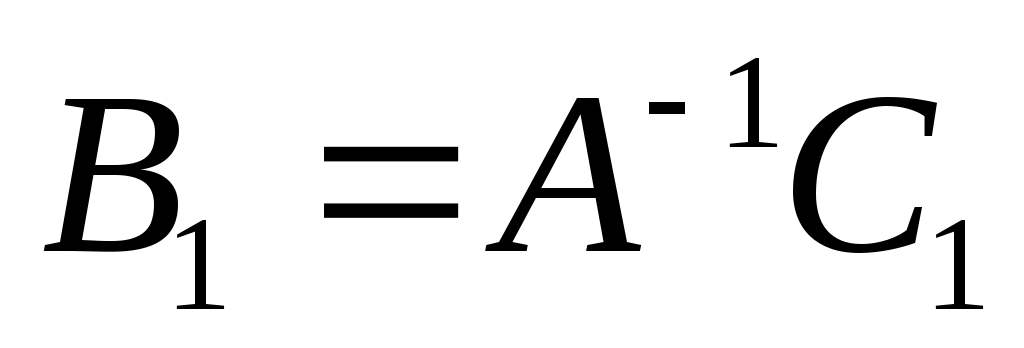 ;
; 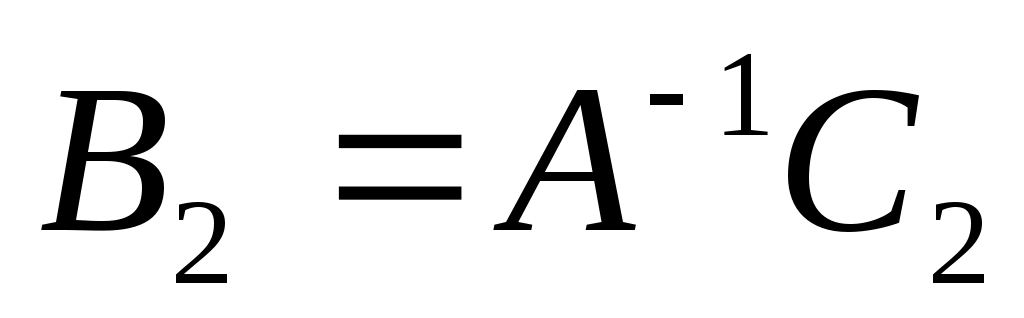
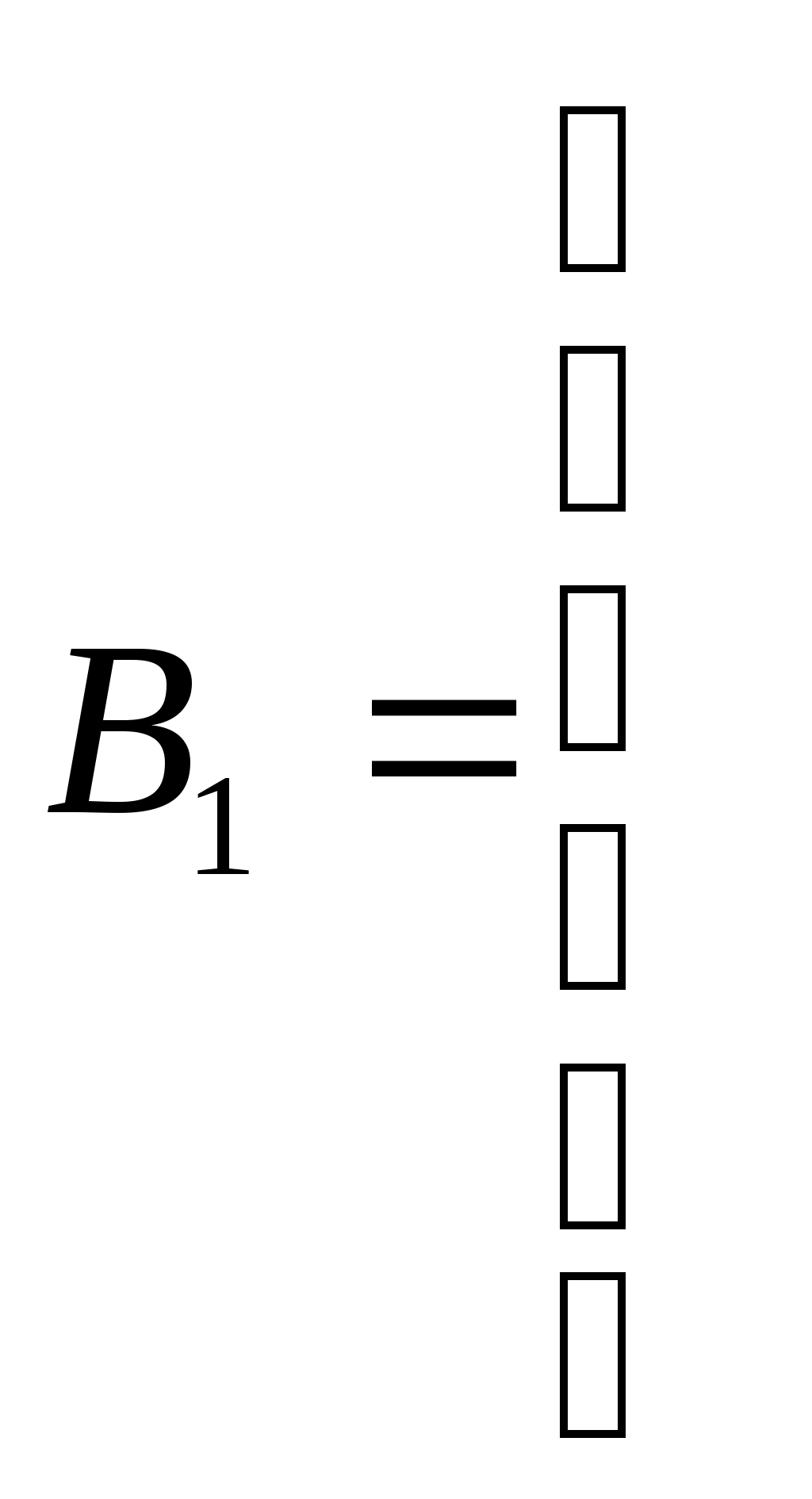
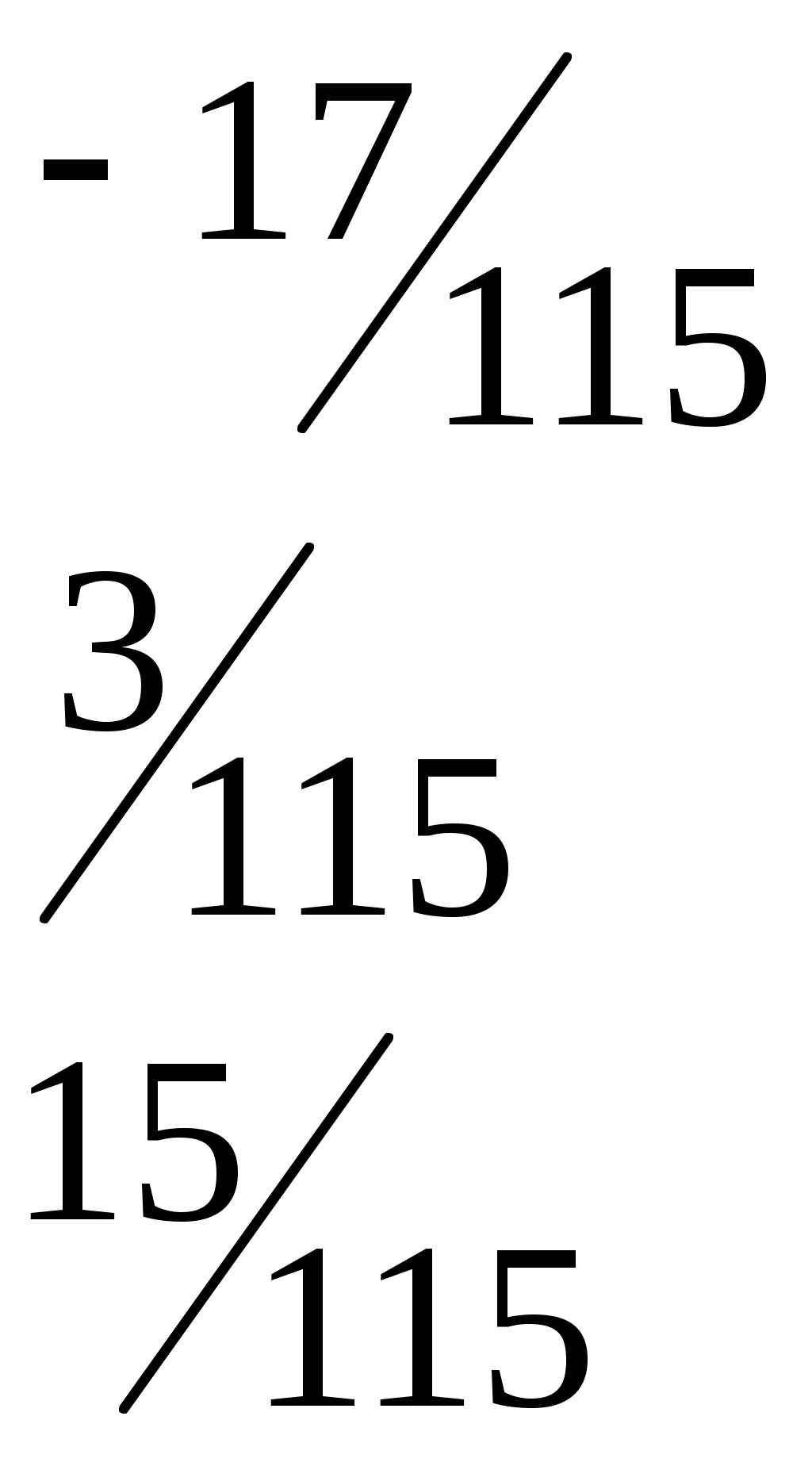
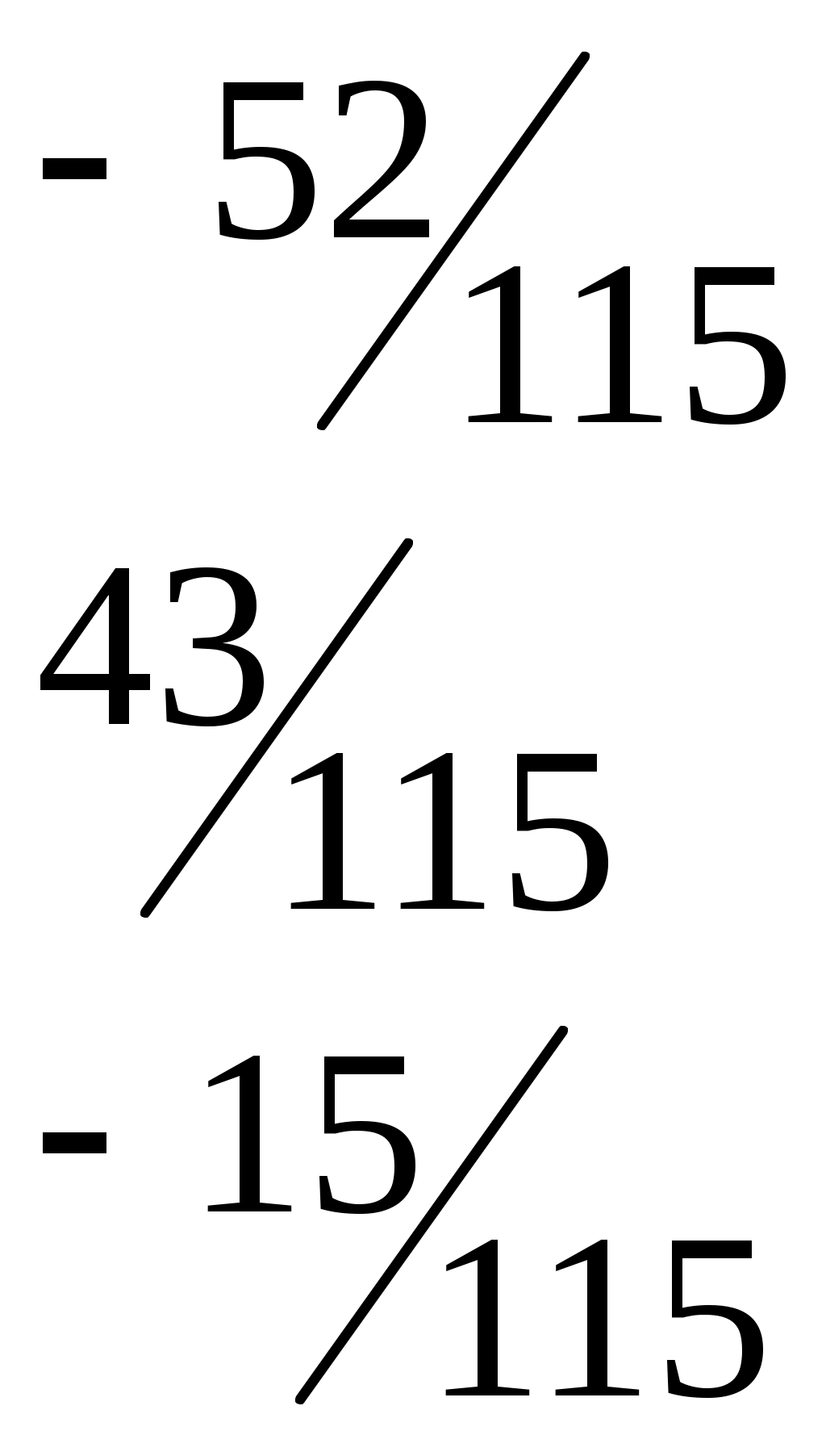
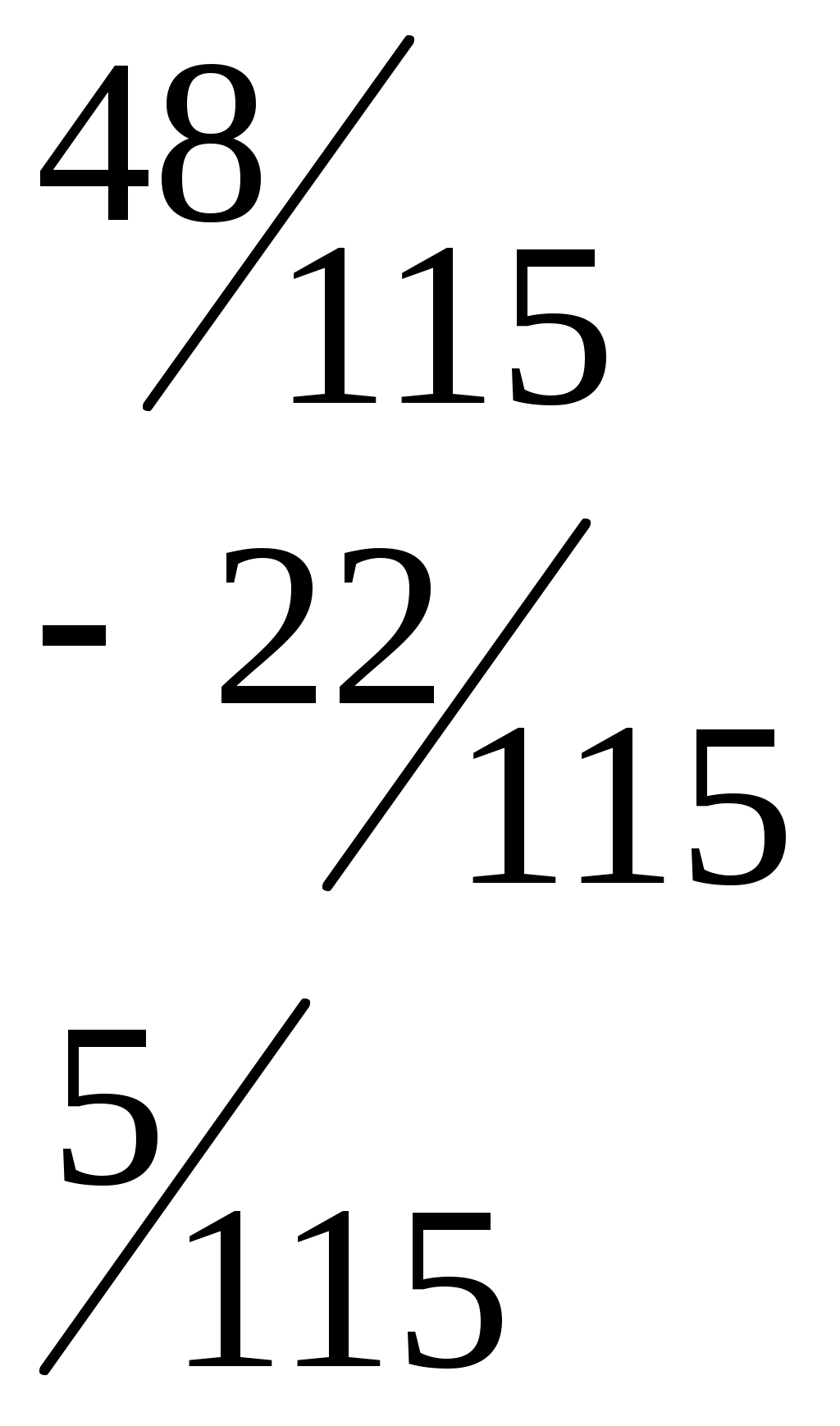
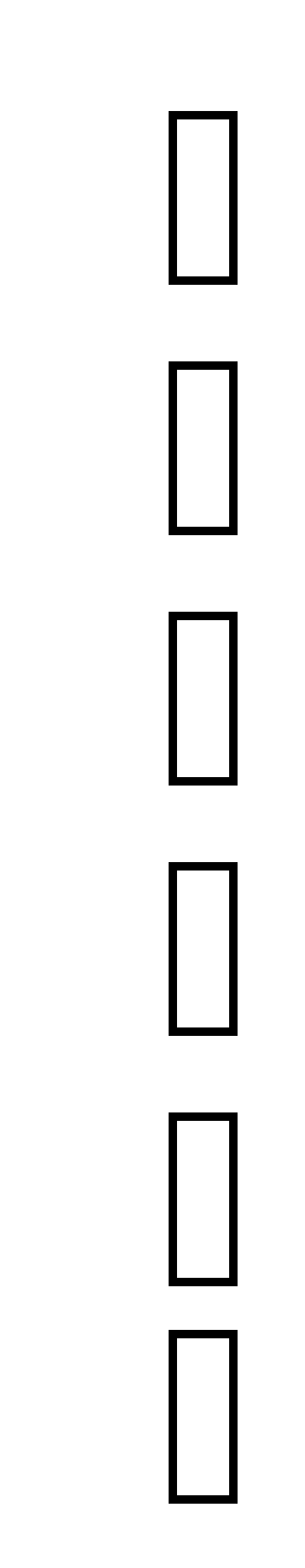
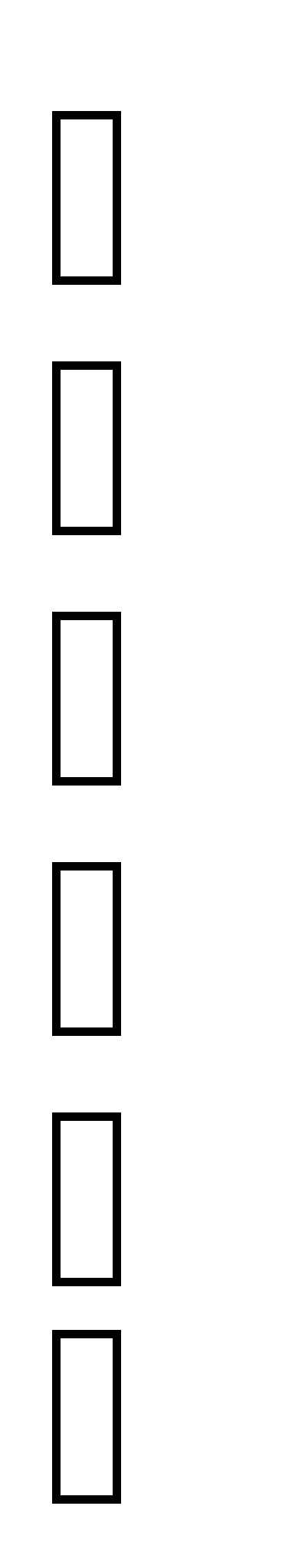
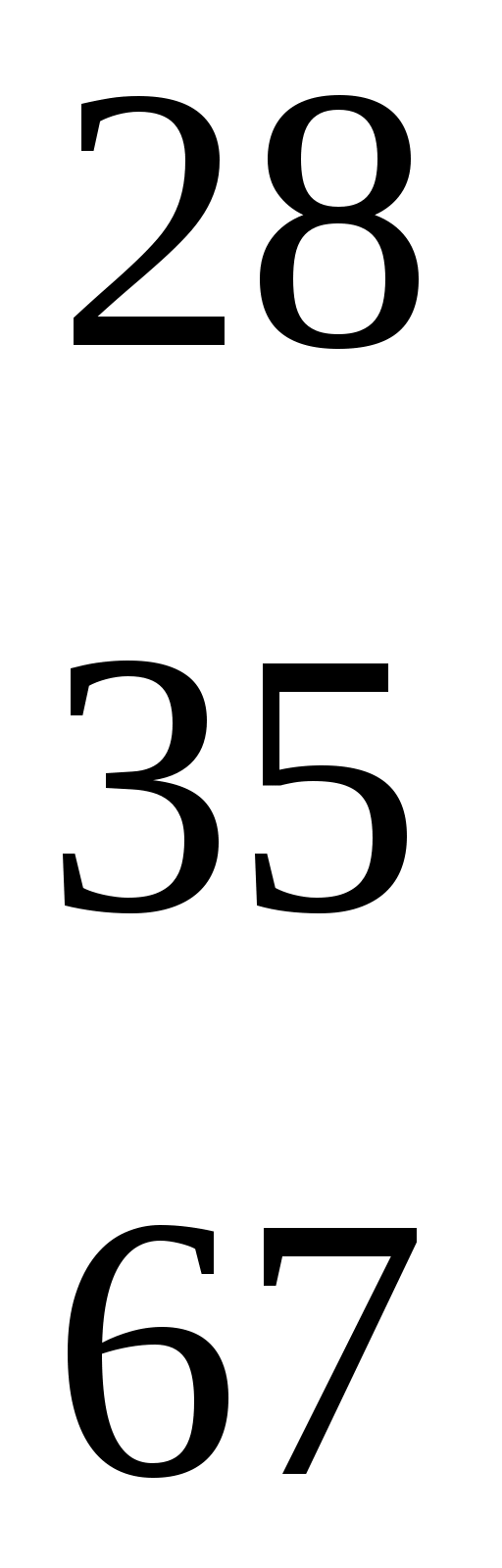
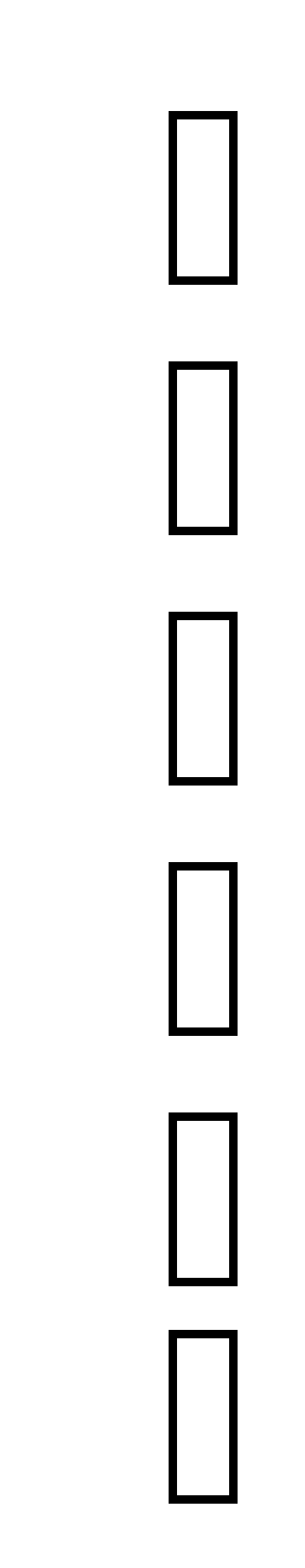 =
= 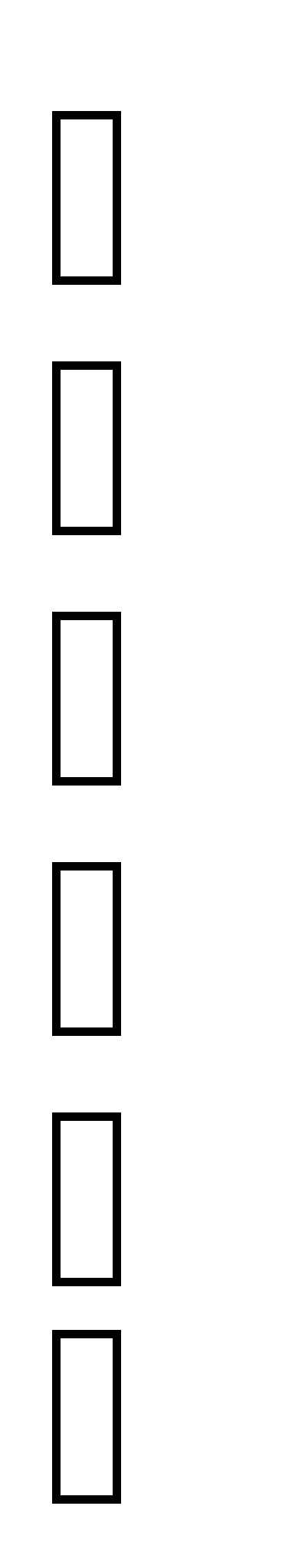
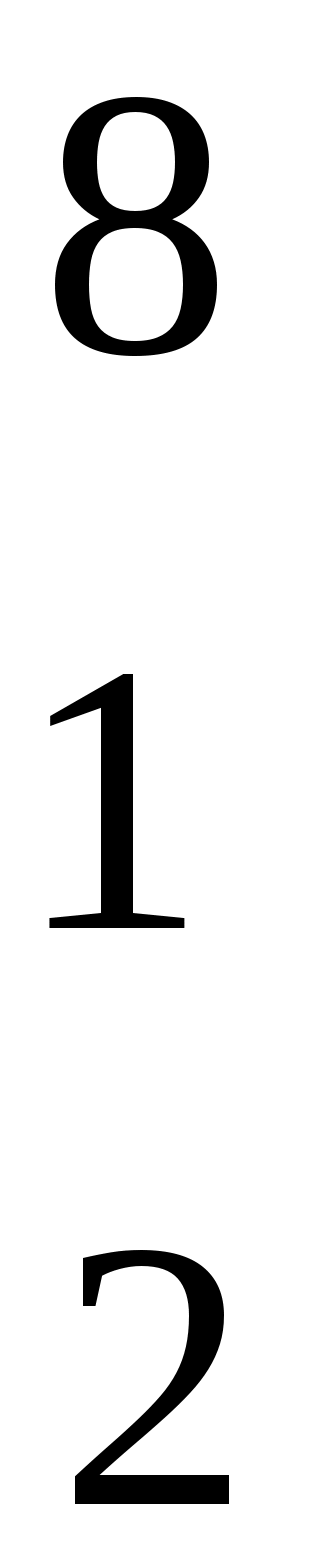
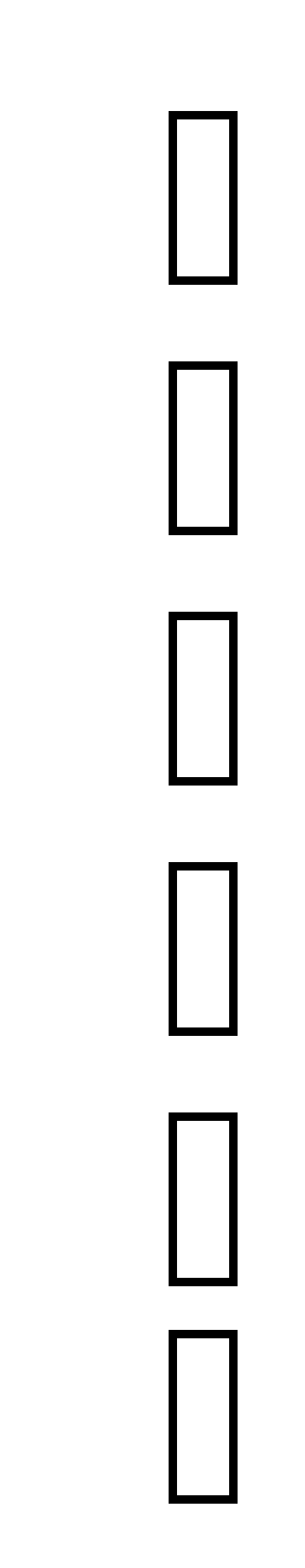

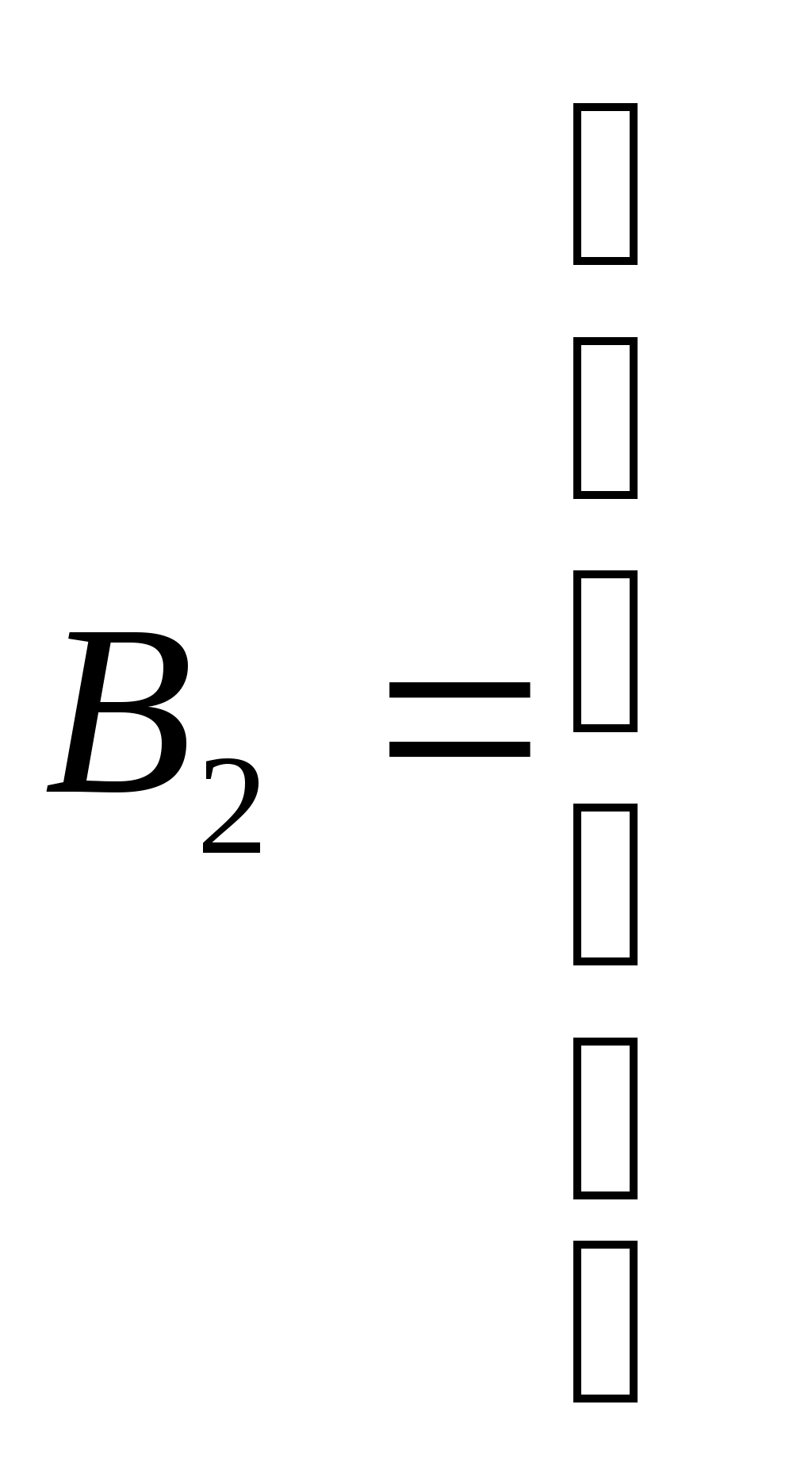
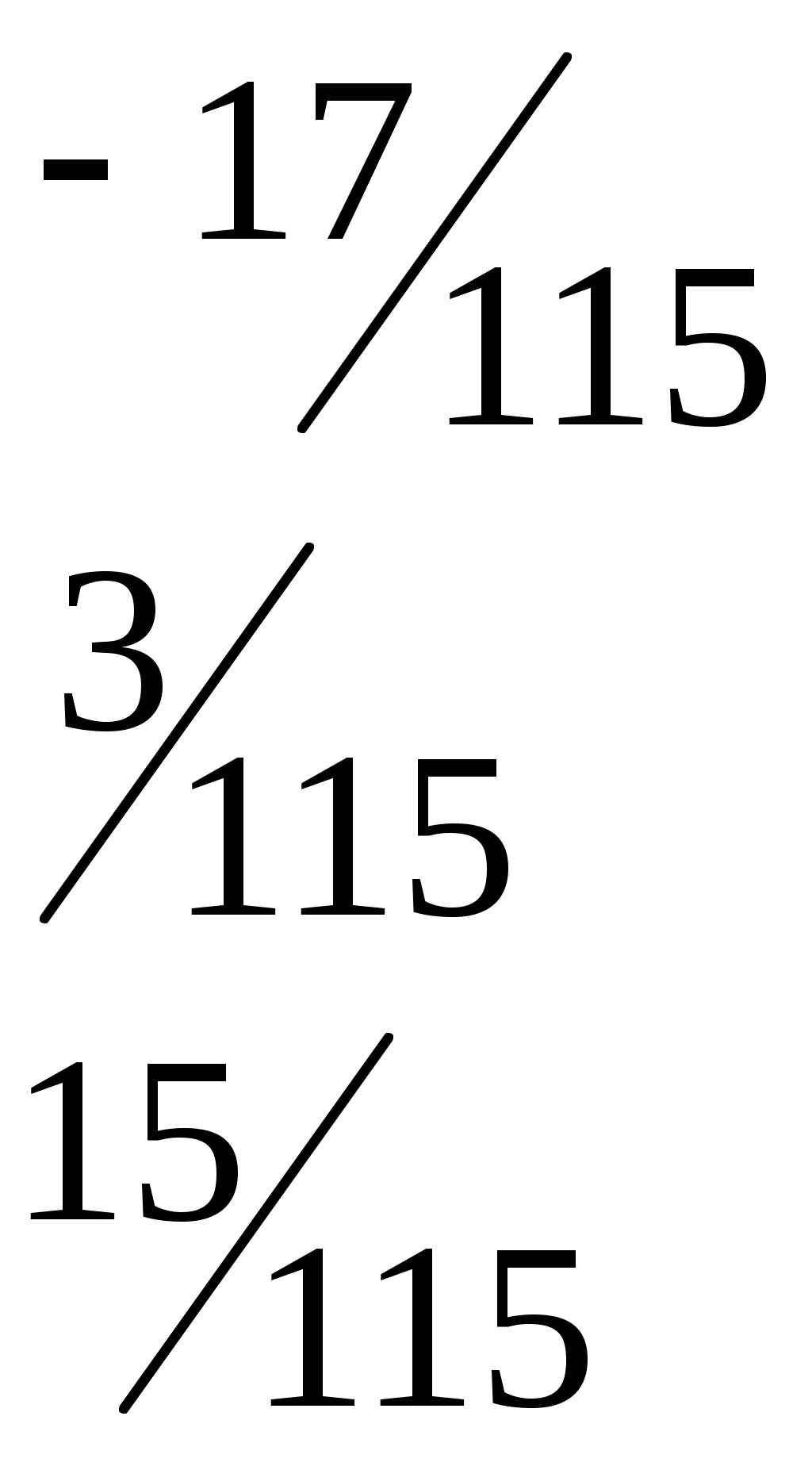
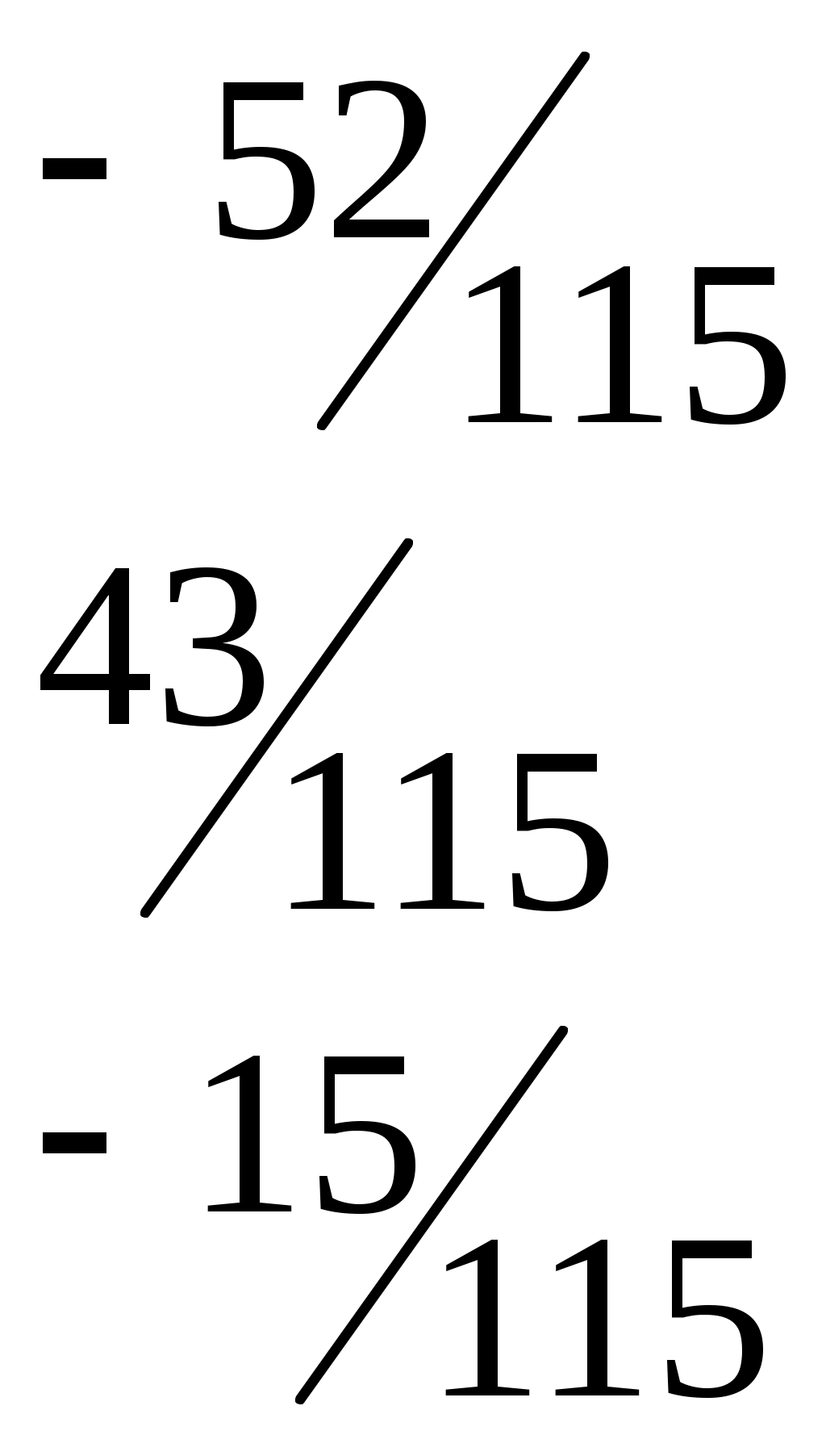
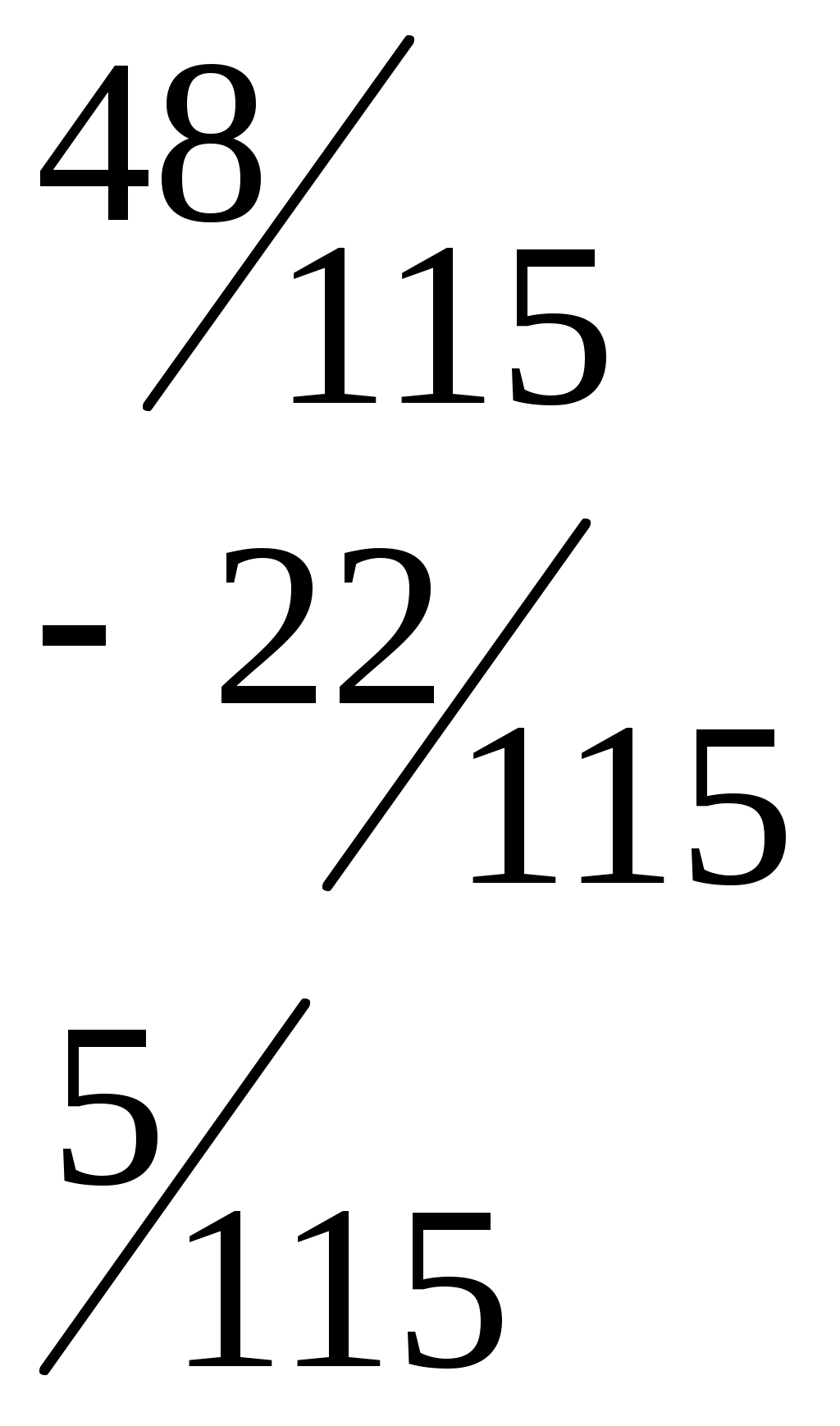
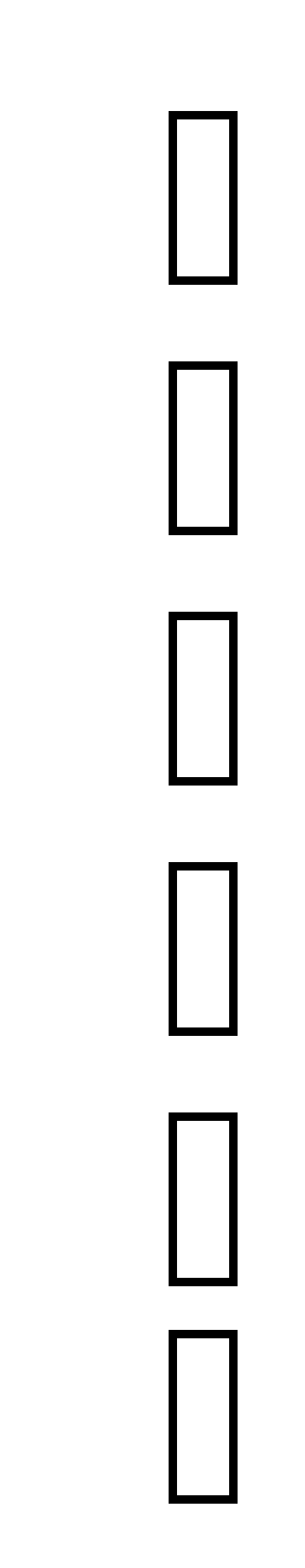
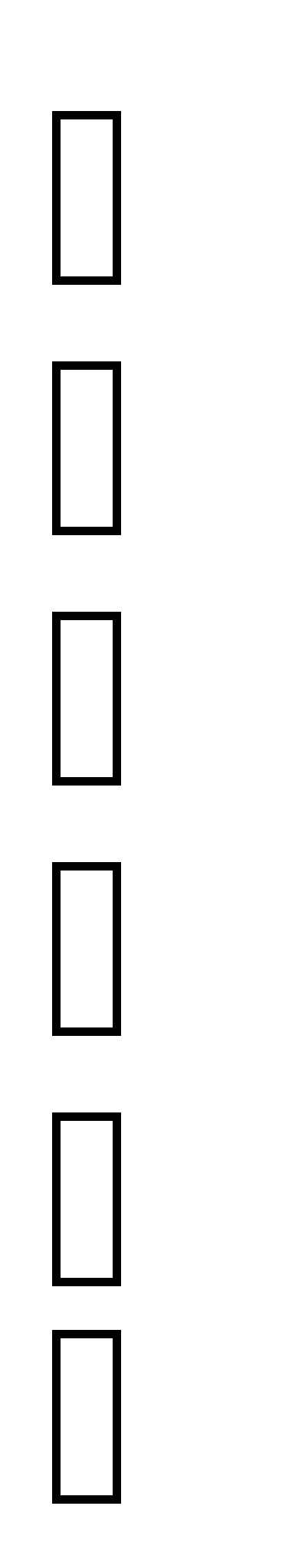
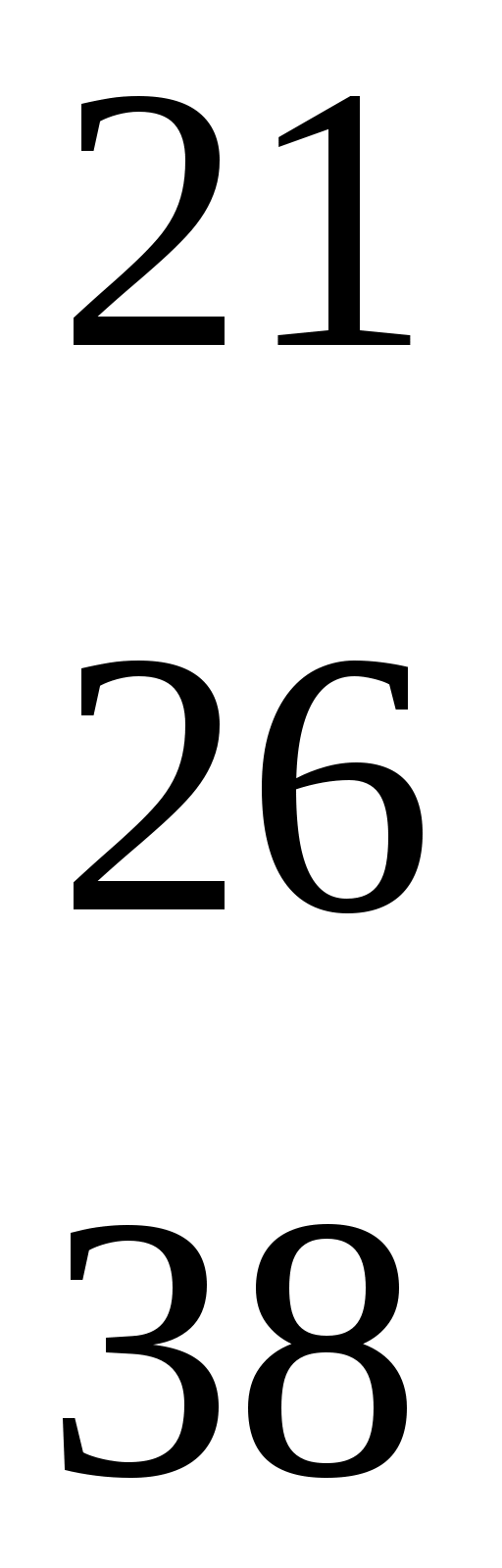
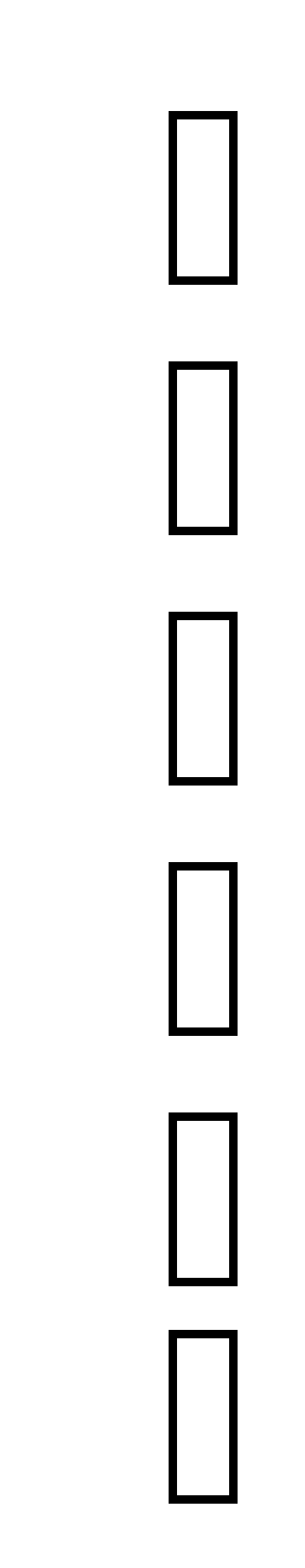 =
= 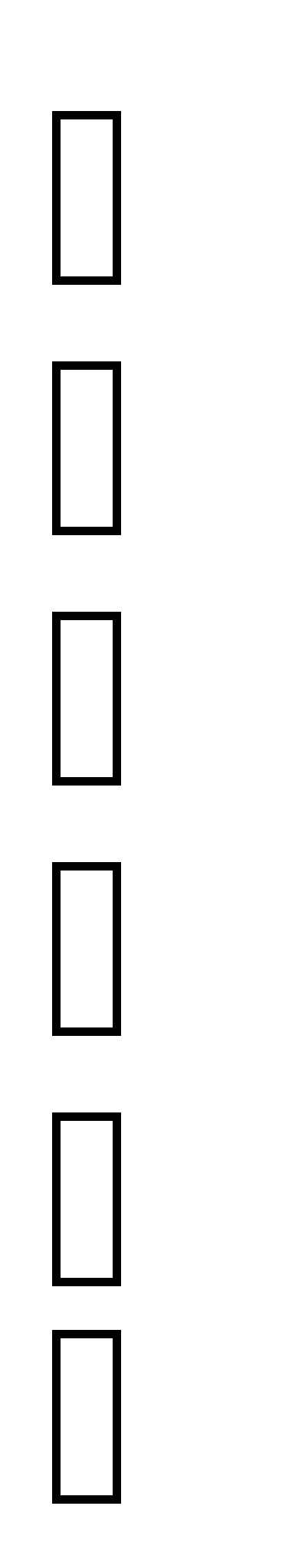
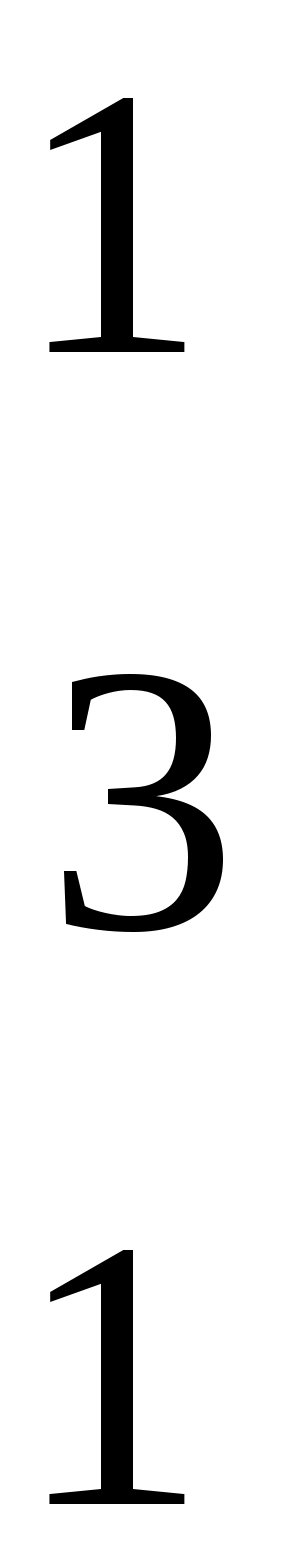
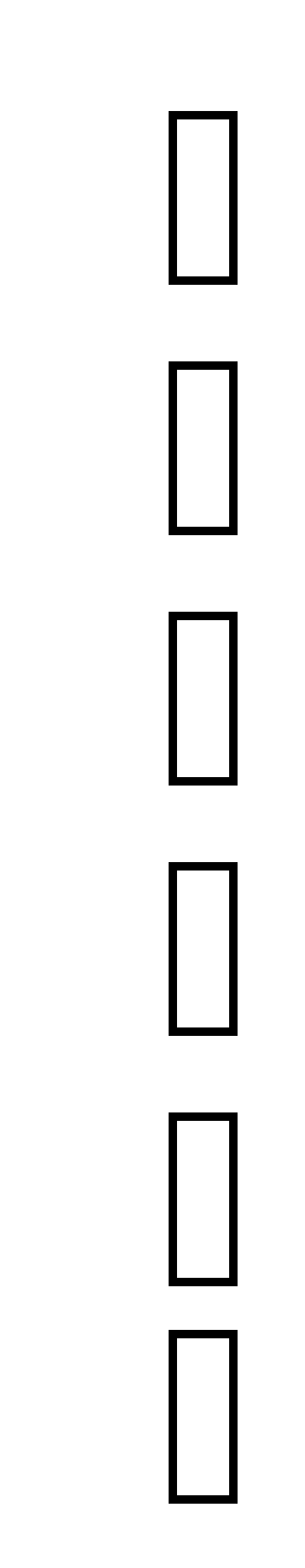
6.Получаем числовой эквивалент расшифрованного слова:
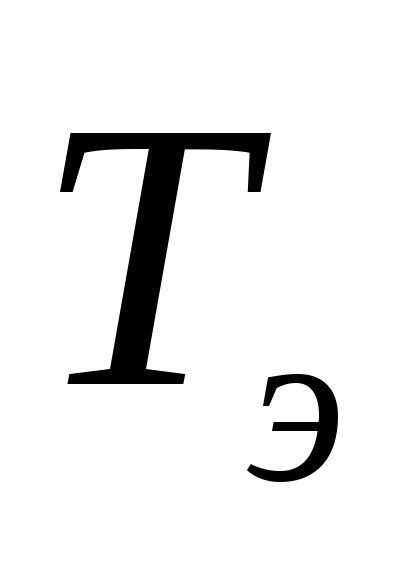 =<8,1,2,1,3,1>, который заменяется символами, в результате получается исходное слово
=<8,1,2,1,3,1>, который заменяется символами, в результате получается исходное слово
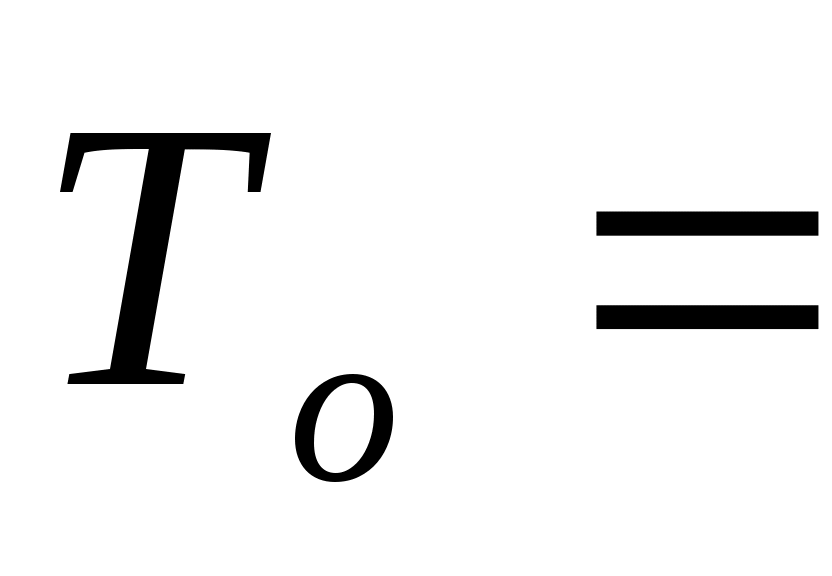 <ЗАБАВА>
<ЗАБАВА>
Пояснение к заданию 3
Асимметричная криптосистема RSA.
Расширенный алгоритм Евклида
-
Выбирают два больших простых числа pиq. Для большей криптостойкости pиqвыбирают равной длины.
-
Вычисляют произведение: n=pq
-
Вычисляют z=(p-1)(q-1) и выбирают число е взаимно простое с z, т.е. НОД (е,z)=1.
-
Для вычисления закрытого (секретного) ключа d решается сравнение
еd 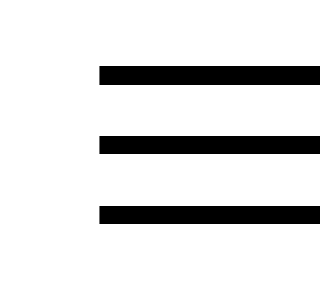 1modz (1)
1modz (1)
Решение (1) имеет вид 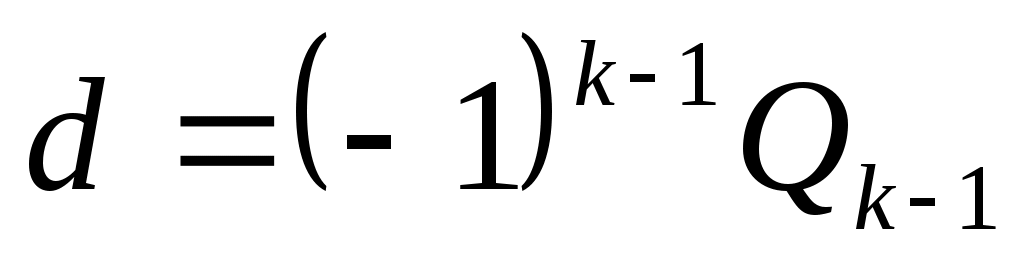
Для вычисления ключа dвоспользуемся расширенным алгоритмом Евклида. Для этого число 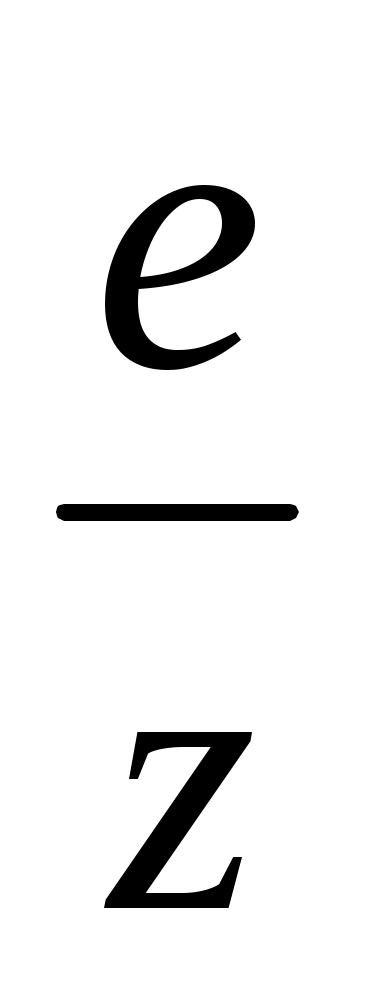 обращается в конечную цепную дробь:
обращается в конечную цепную дробь:
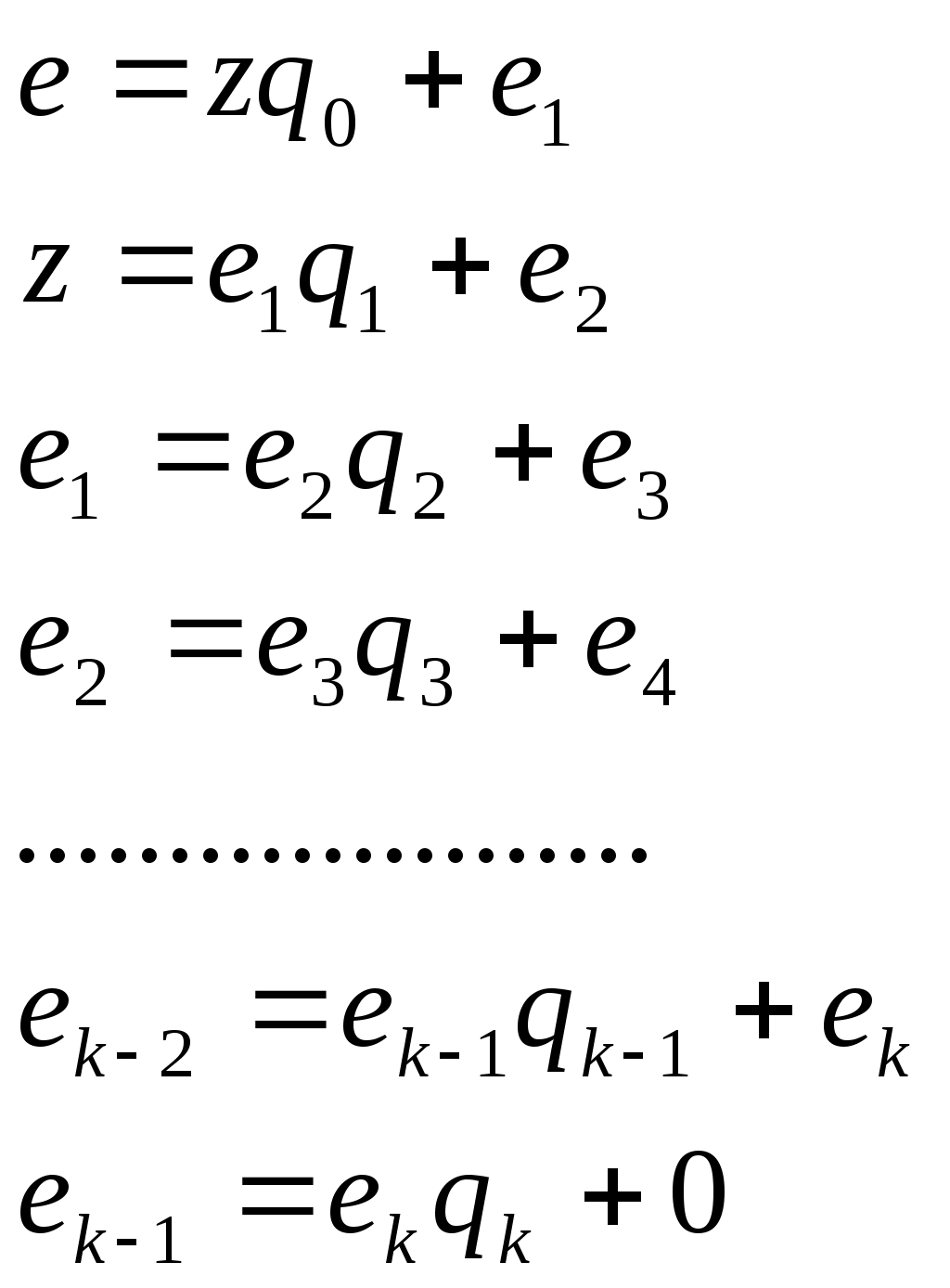
Цепная дробь имеет вид: 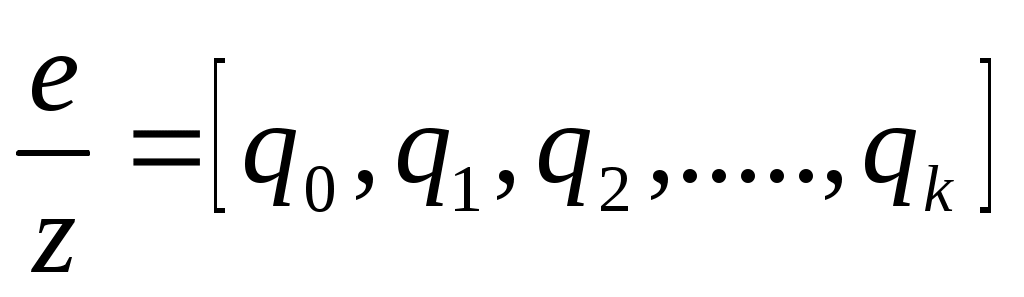 , а последовательности
, а последовательности 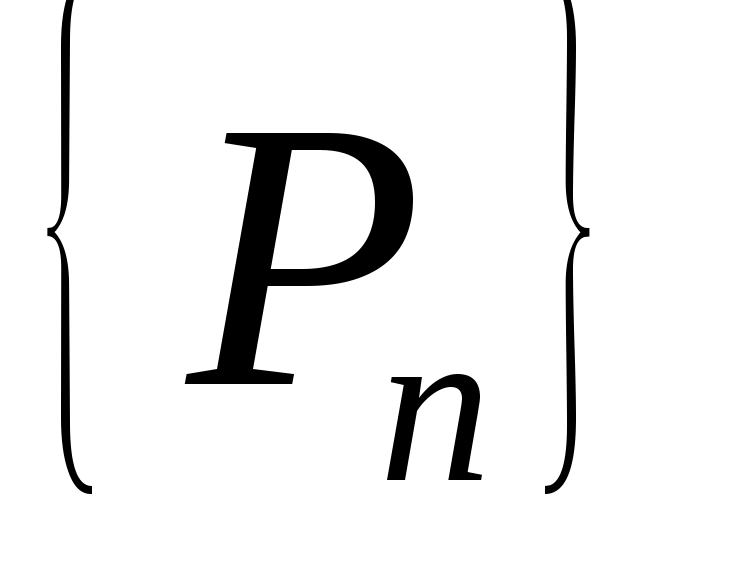 и
и 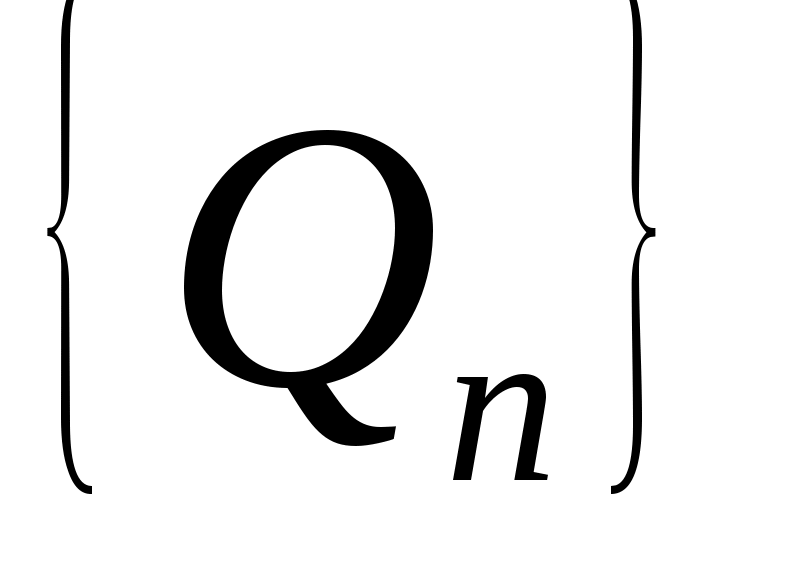 числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:
числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:
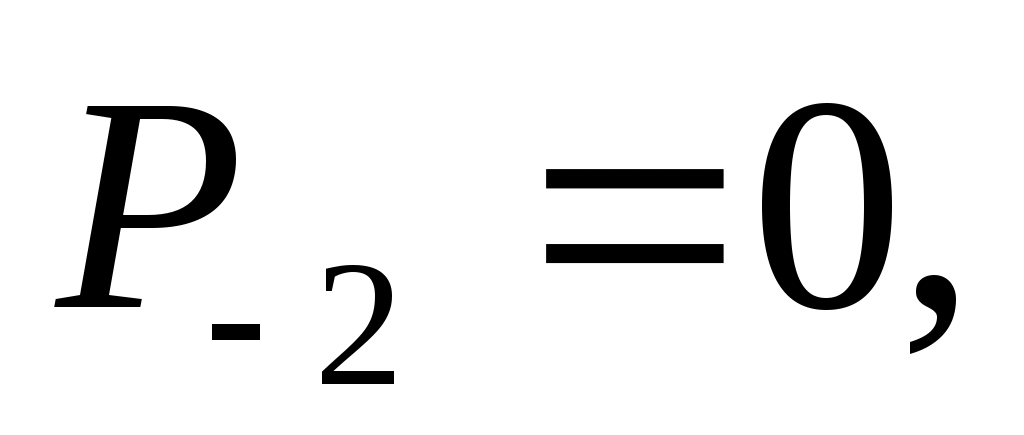
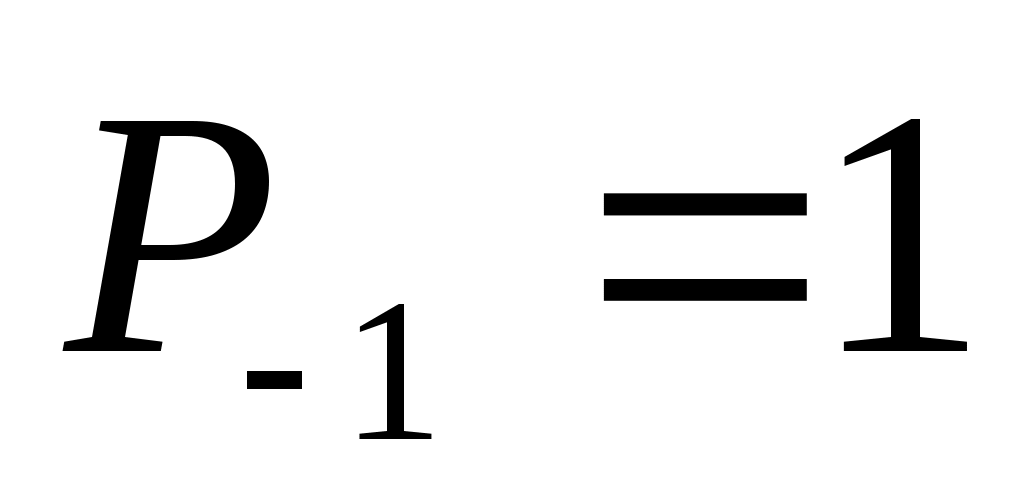 ,
, 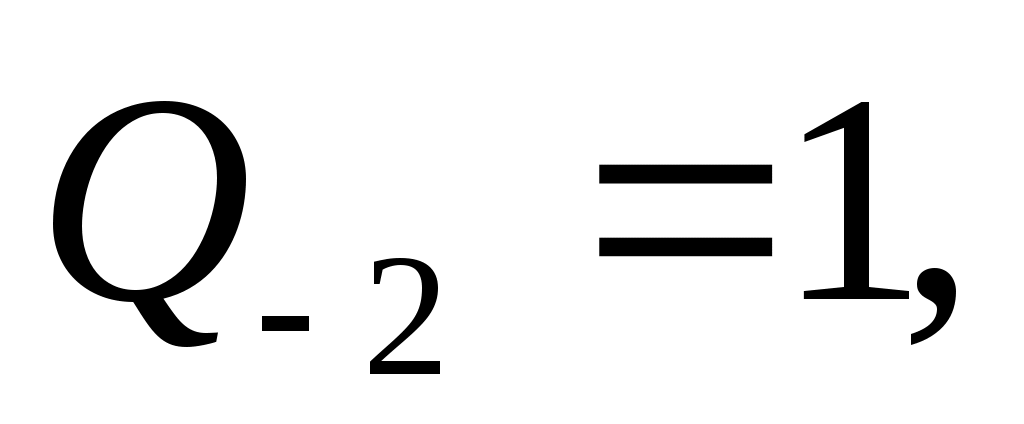
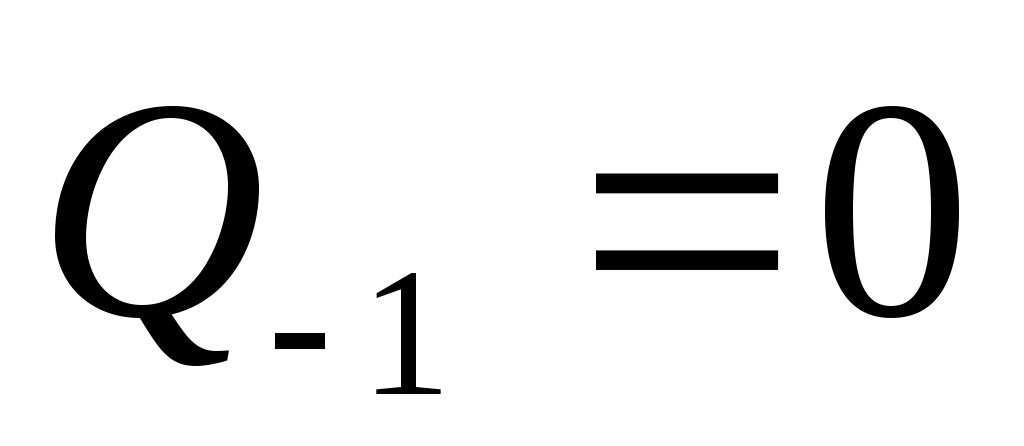 .
.
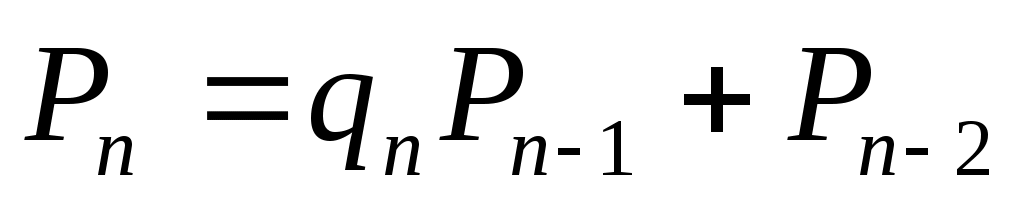 ,
, 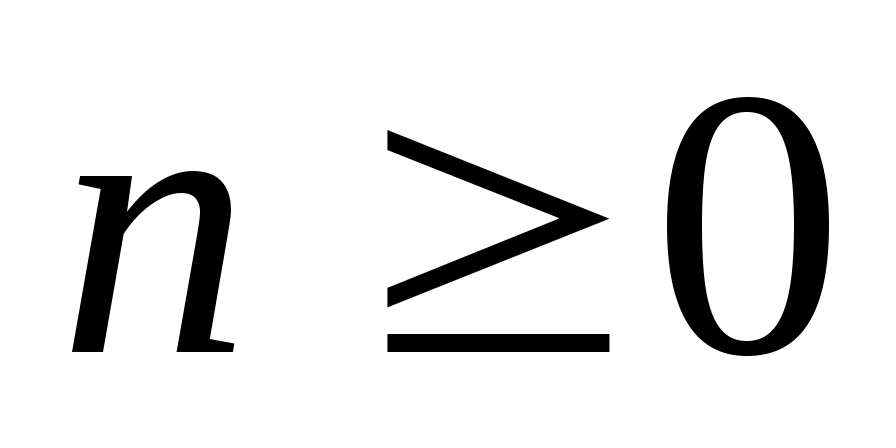
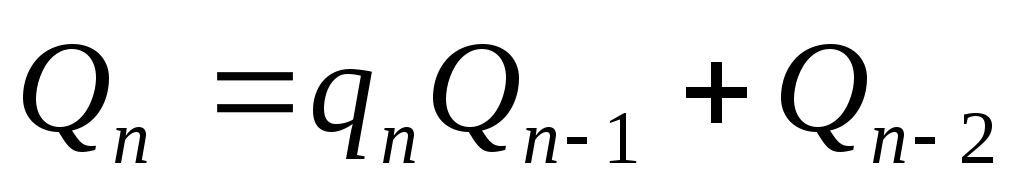 ,
, 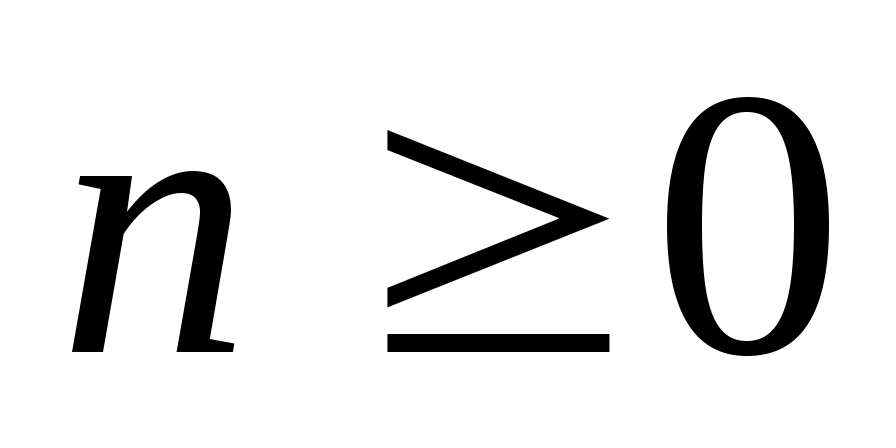
Их вычисления удобно оформить в виде таблицы:
1.3.5. Биграммный шифр Плейфейра
Шифр Плейфейра, изобретенный в 1854 г., является наиболее известным биграммным шифром замены. Он применялся Великобританией во время первой мировой войны. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.
Для удобства запоминания шифрующей таблицы отправителем и получателем сообщений можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей таблицей Трисемуса из предыдущей задачи ( рис. 1.5).
Процедура шифрования включает следующие шаги.
-
Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.
-
Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
2а.Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы А и Й в табл. на рис.2.6), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это – буквы АЙОВ. Пара букв АЙ отображается в пару ОВ. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста.)
2б.Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в.Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.)
Задача 1.10. Зашифровать биграммным шифром Плейфера текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Решение.Разобьём этот текст на биграммы:
ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы (рис. 1.5) в следующую последовательность биграмм шифртекста
ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ
При дешифровании применяется обратный порядок действий.
Шифрование биграммами резко повышает стойкость шифров к вскрытию. Хотя книга И.Трисемуса "Полиграфия" была относительно доступной, описанные в ней идеи получили признание лишь спустя три столетия. По всей вероятности, это было обусловлено плохой осведомленностью криптографов о работах богослова и библиофила Трисемуса в области криптографии.
Пояснение к заданию 2
Методы шифрования
2.1. Метод перестановок на основе маршрутов
Гамильтона
Этот метод реализуется путем выполнения следующих шагов.
Шаг 1. Исходный текст разбивается на блоки. Если длина шифруемого текста не кратна длине блока, то на свободные места последнего блока помещаются служебные символы-заполнители(например,*)
Шаг 2. Символами блока заполняется таблица, в которой для каждого порядкового номера символа в блоке отводится вполне определенное место (рис. 2.1).



Исходная
таблица
Маршрут 1
Маршрут 2
Рисунок 2.1 - Вариант 8-элементной таблицы и маршрутов
Гамильтона.
Шаг 3. Считывание символов из таблицы осуществляется по одному из маршрутов. Увеличение числа маршрутов повышает криптостойкость шифра. Маршруты выбирают либо последовательно, либо их очерёдность задаётся ключом К.
Шаг 4. Зашифрованная последовательность символов разбивается на блоки фиксированной длины L. Величина L может отличаться от длины блоков, на которые разбивается исходный текст на шаге 1.
Расшифрование производится в обратном порядке.
Задача 2.1. Требуется зашифровать текст 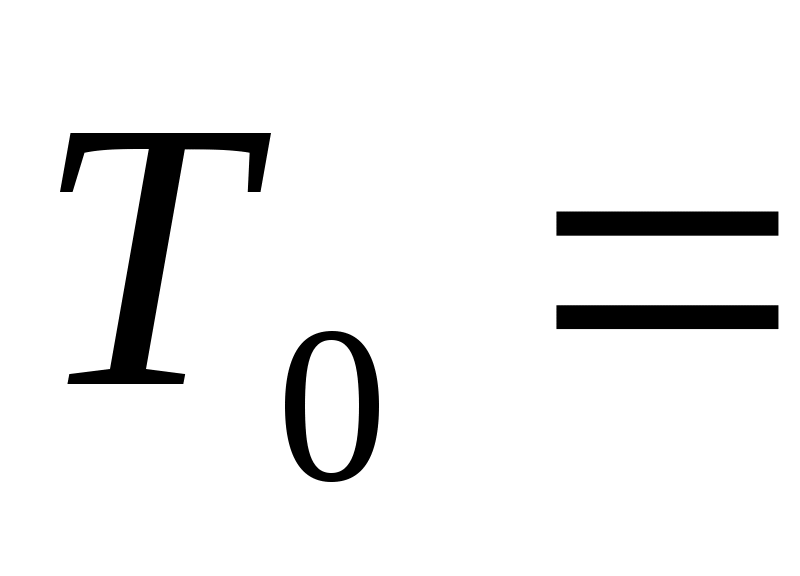 <МЕТОДЫ ПЕРЕСТАНОВКИ>. Ключ и длины зашифрованных блоков равны: К=<2,1,1>, L=4. Для шифрования использовать таблицу и два маршрута, представленные на рис.2.1.
<МЕТОДЫ ПЕРЕСТАНОВКИ>. Ключ и длины зашифрованных блоков равны: К=<2,1,1>, L=4. Для шифрования использовать таблицу и два маршрута, представленные на рис.2.1.
Решение. Воспользуемся вышеизложенной методикой построения шифра по шагам.
Шаг 1. Исходный текст разбивается на 3 блока:
Блок 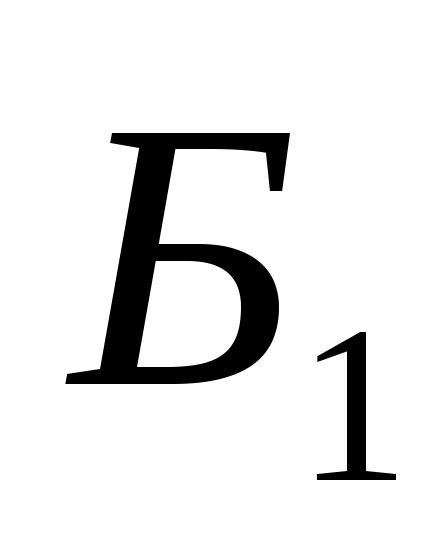 =<МЕТОДЫ П>
=<МЕТОДЫ П>
Блок 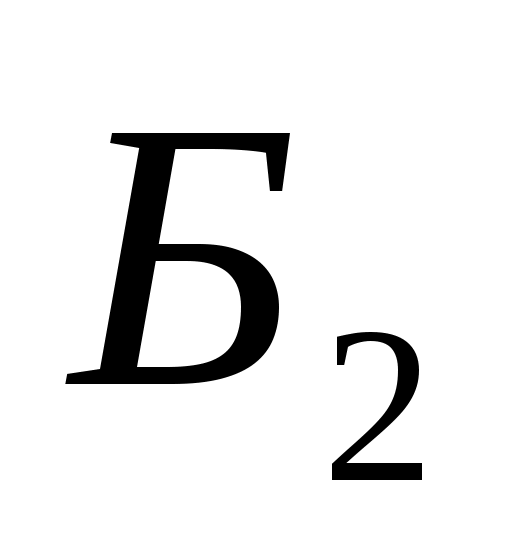 =<ЕРЕС ТАНО>
=<ЕРЕС ТАНО>
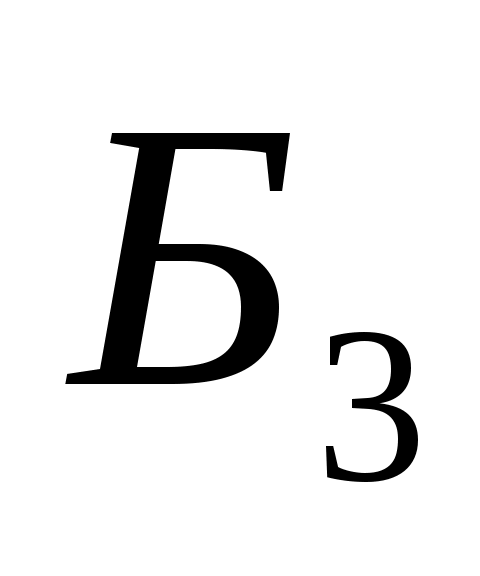 =<ВКИ*****>
=<ВКИ*****>
Шаг 2. Заполняется 3 матрицы с маршрутами 2,1,1 (рис.2.2.)


Маршрут 2

Маршрут 1
Маршрут 1
Рисунок 2.2 - Шифрование с помощью маршрутов Гамильтона.
Шаг 3. Получение шифртекста путём расстановки символов в соответствии с маршрутами.
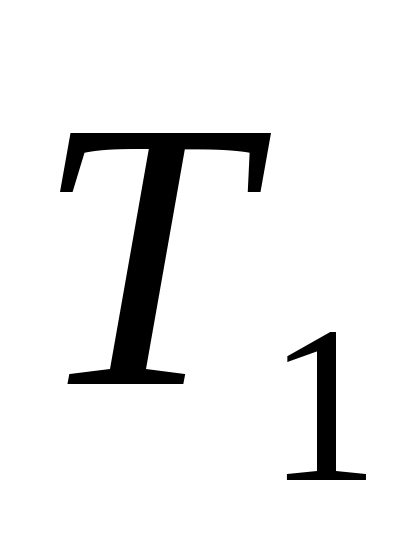 =<ОП_ТМЕЫДЕСРЕТАОНИ*КВ****>
=<ОП_ТМЕЫДЕСРЕТАОНИ*КВ****>
Шаг4. Разбиение на блоки шифртекста
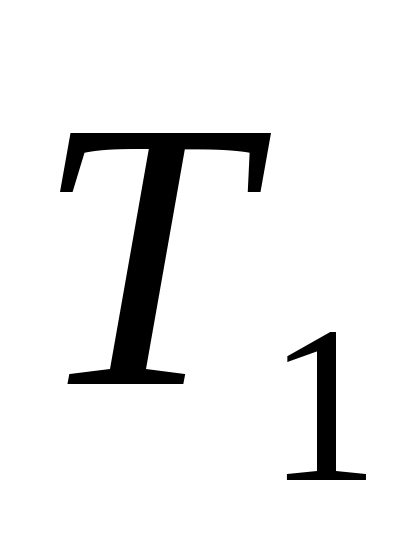 =<ОП_Т МЕЫД ЕСРЕ ТАОН И*КВ ****>
=<ОП_Т МЕЫД ЕСРЕ ТАОН И*КВ ****>
Возможно применение и других маршрутов.
2.2. Аналитические методы шифрования
Среди аналитических методов наибольшее распространение получили методы, основанные на использовании матриц. Зашифрование К-го блока исходной информации, представленного в виде вектора 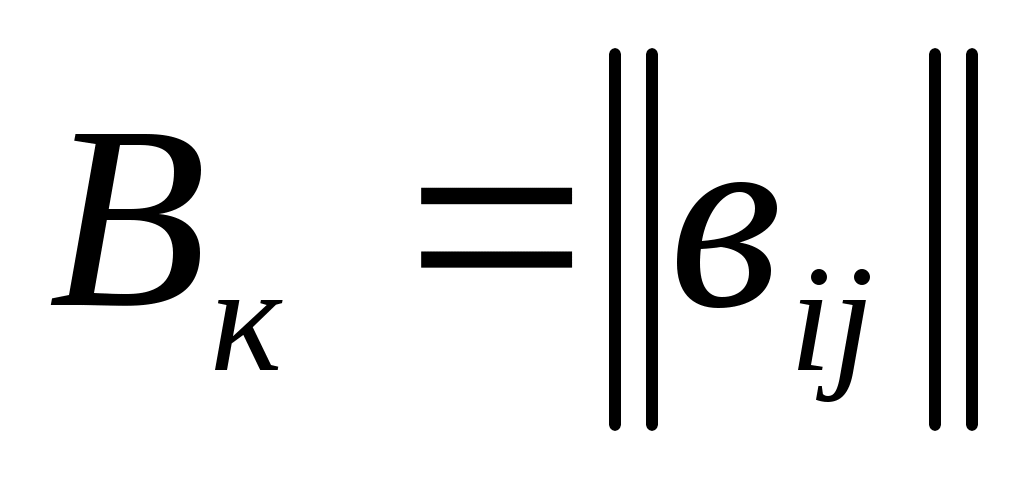 осуществляется путём перемножения матрицы ключа
осуществляется путём перемножения матрицы ключа 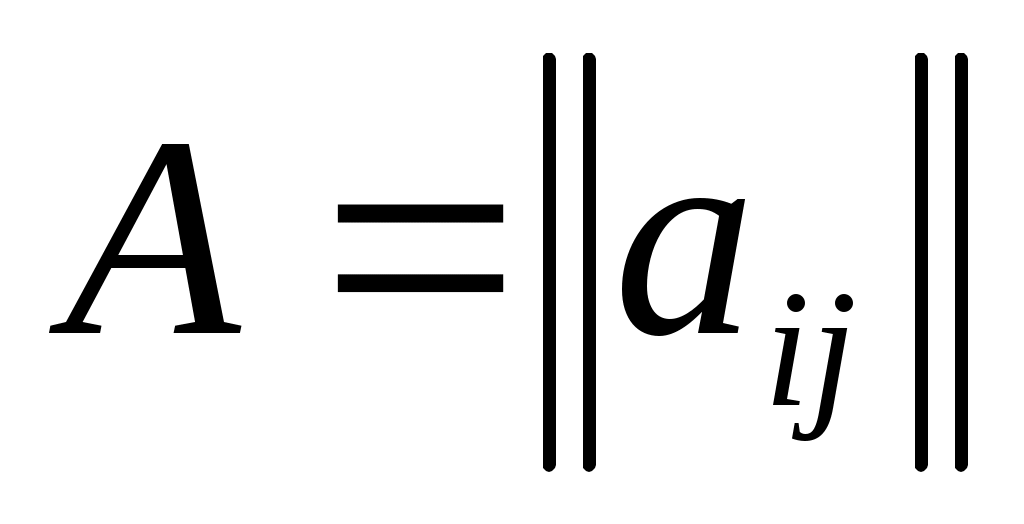 и вектора
и вектора 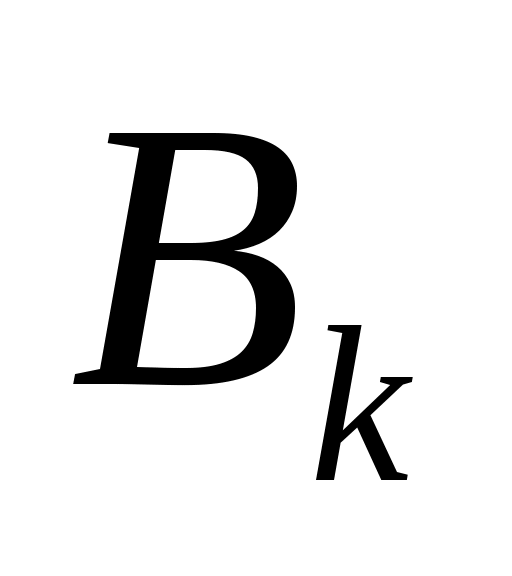 . В результате перемножения получается блок шифртекста в виде вектора
. В результате перемножения получается блок шифртекста в виде вектора 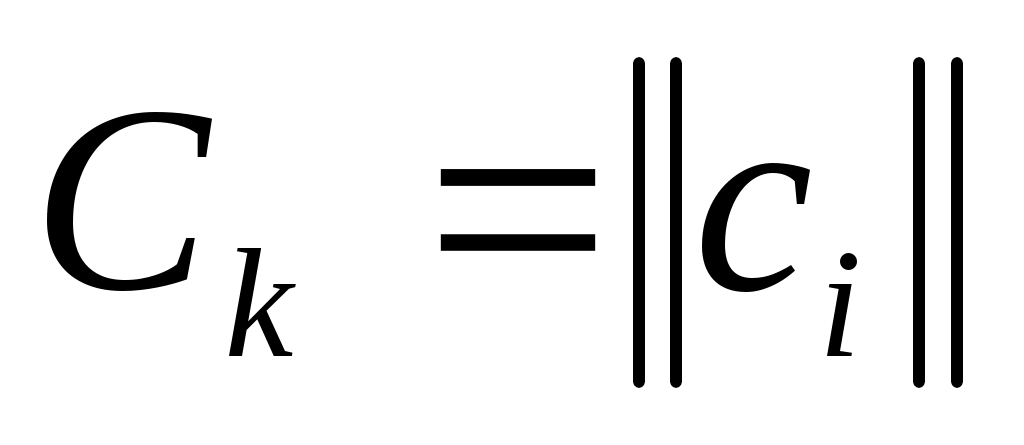 , где элементы вектора
, где элементы вектора 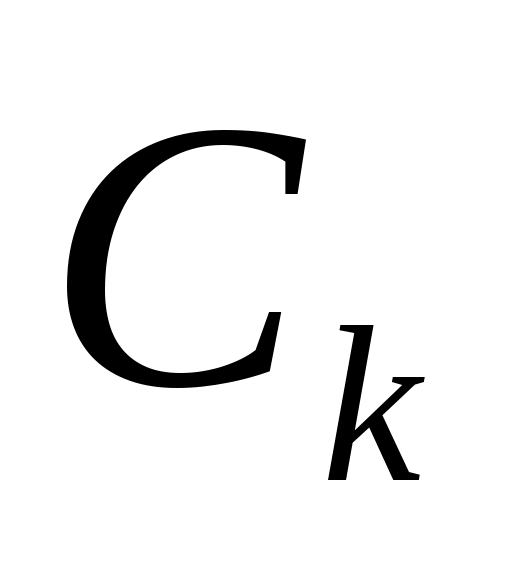 определяются по формуле:
определяются по формуле:
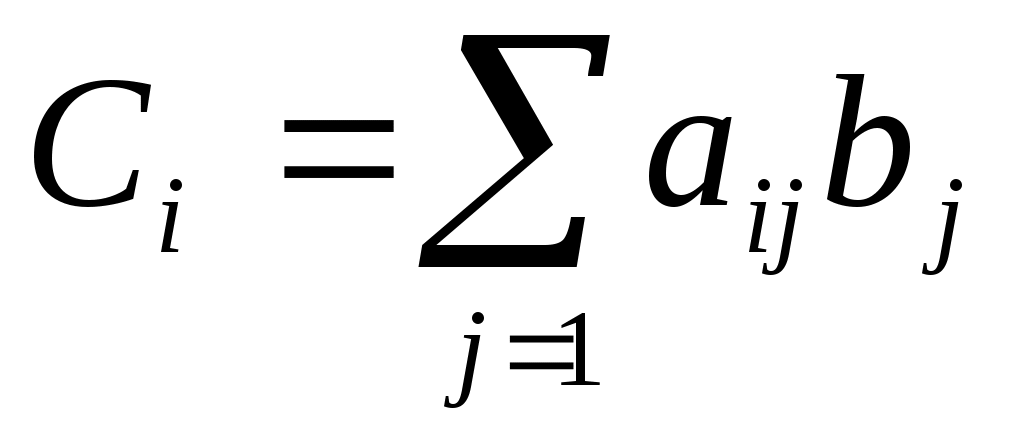 .
.
Расшифрование информации осуществляется путём последовательного перемножения векторов 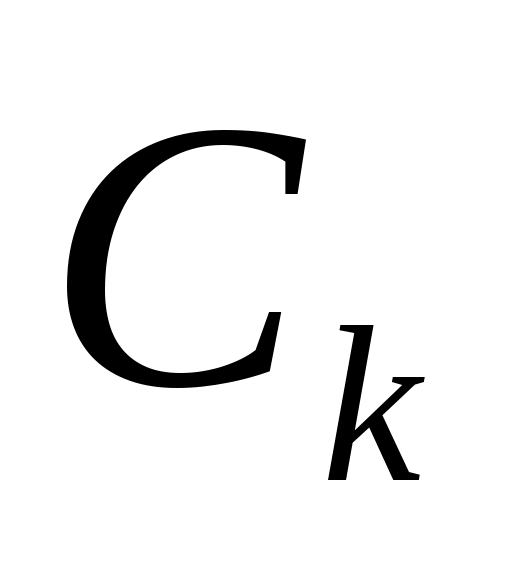 и обратной матрицы
и обратной матрицы 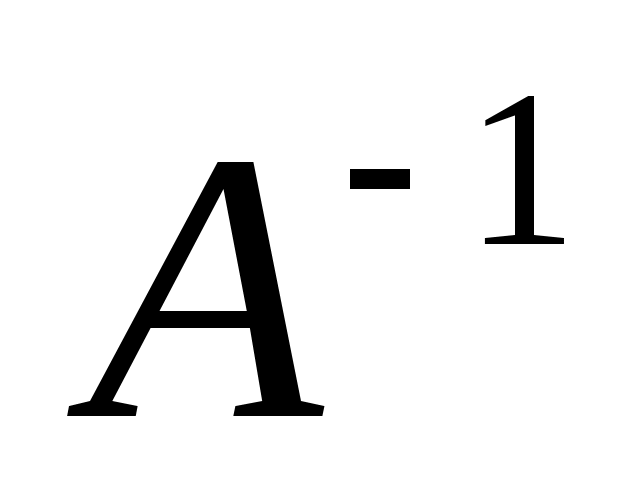 .
.
Задача 2.2. Требуется зашифровать слово 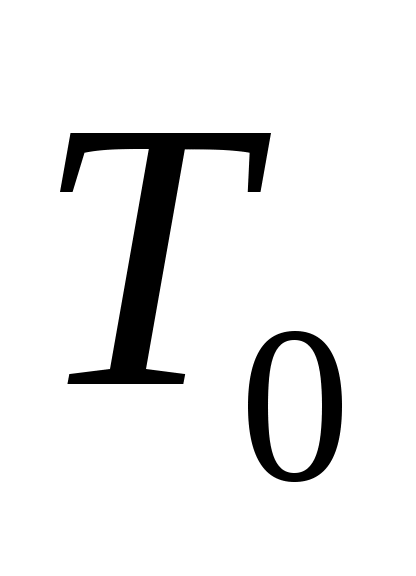 =<ЗАБАВА> с помощью матрицы-ключа А.
=<ЗАБАВА> с помощью матрицы-ключа А.
A=


Решение.
1.Определим числовой эквивалент исходного слова как последовательность соответствующих порядковых номеров букв слова 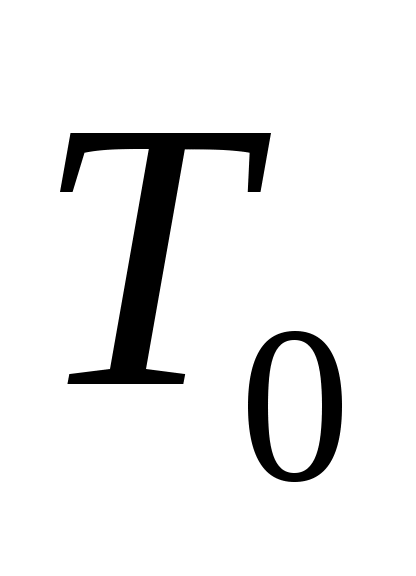 :
:
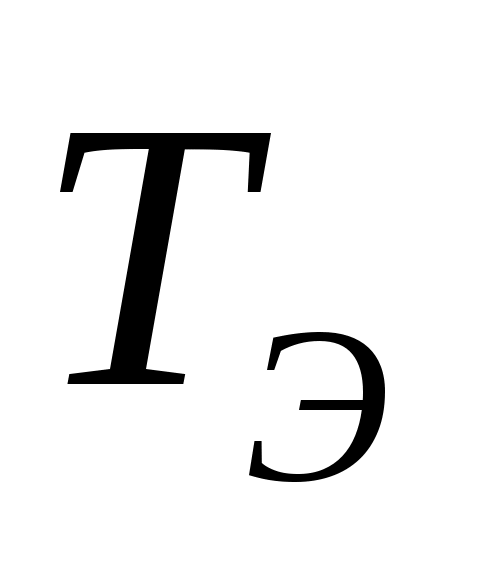 =<8,1,2,1,3,1>
=<8,1,2,1,3,1>
2.Разобьём 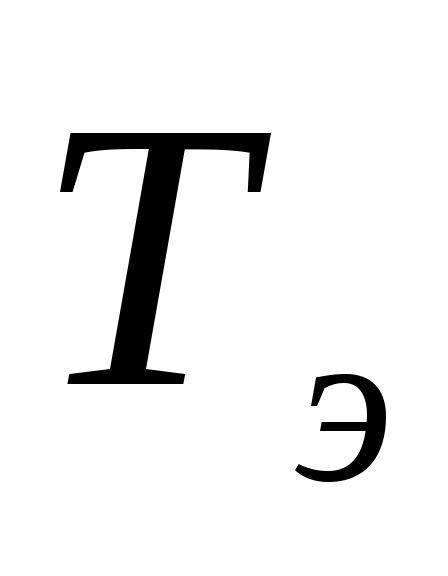 на два вектора
на два вектора 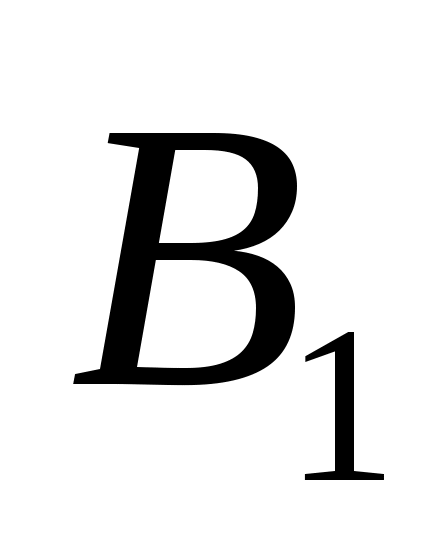
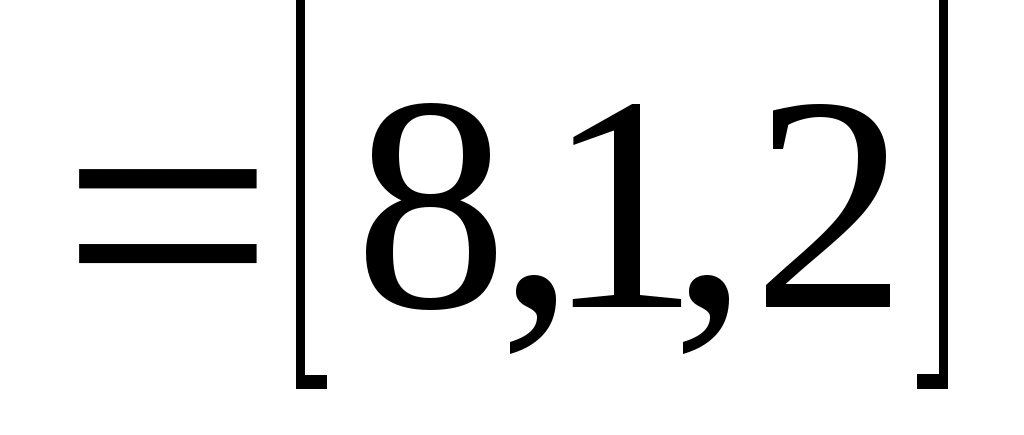 и
и 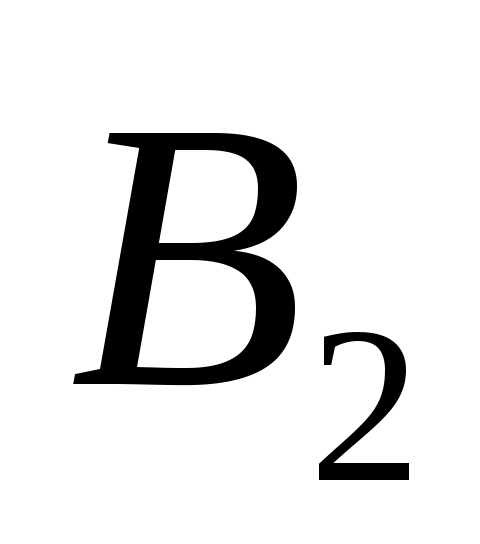
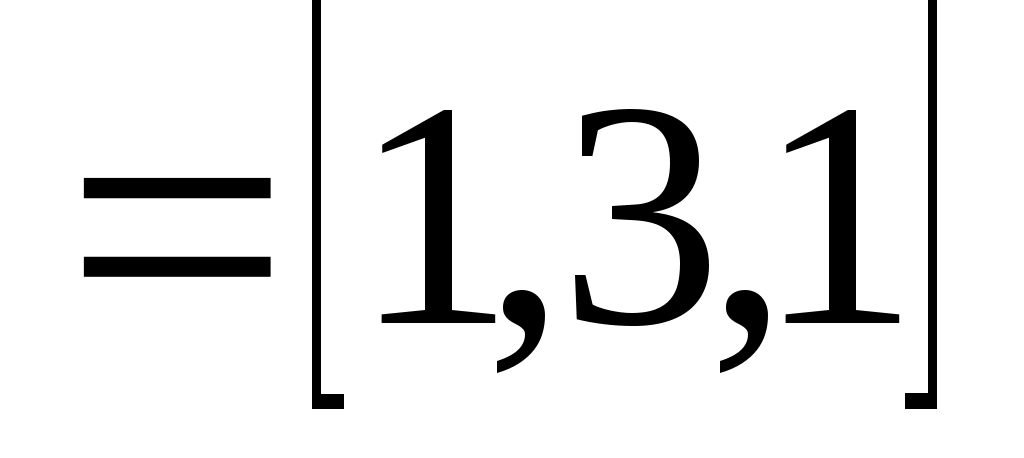
3. Умножим матрицу А на векторы 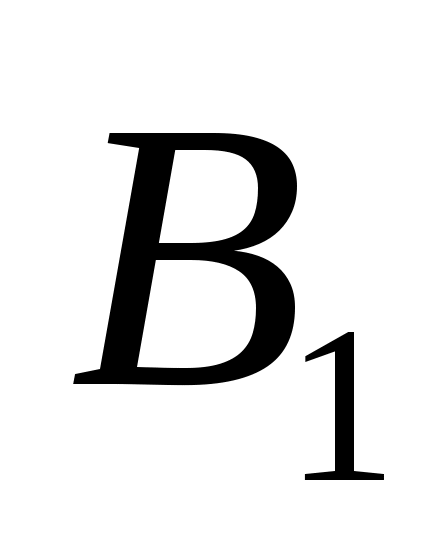 и
и 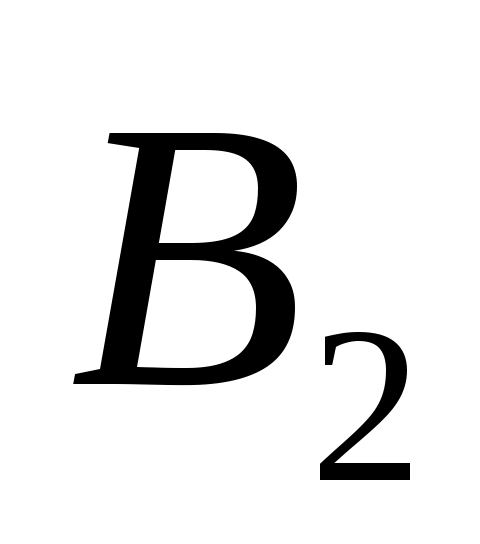 :
:
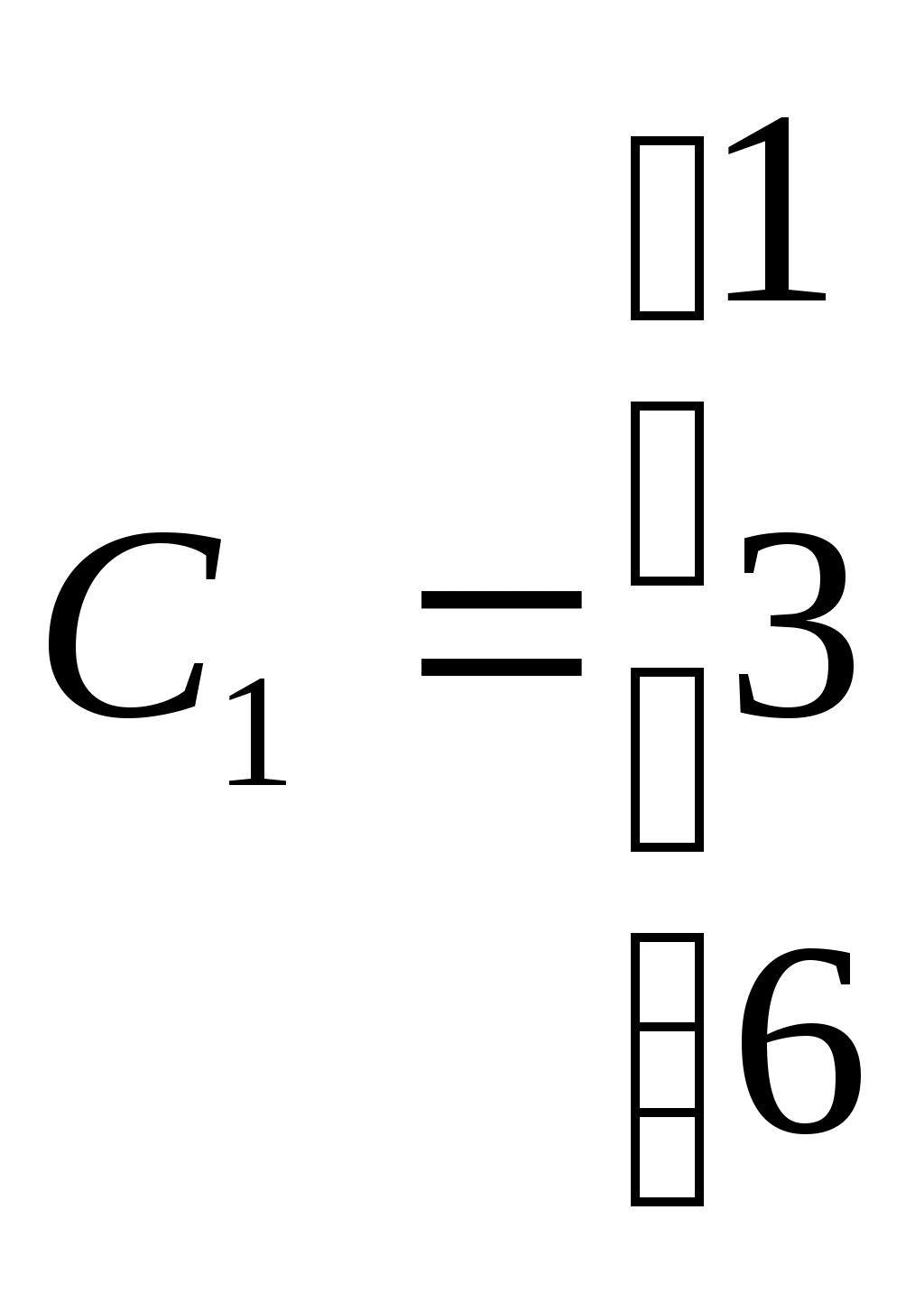


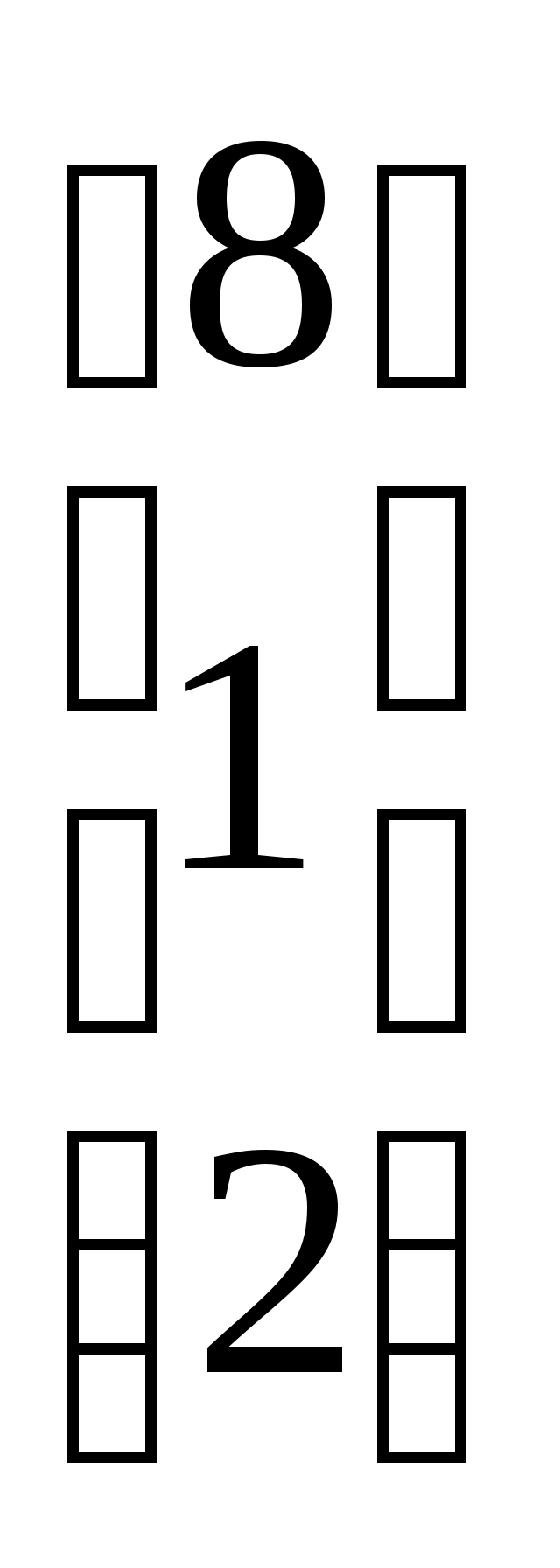 =
= 
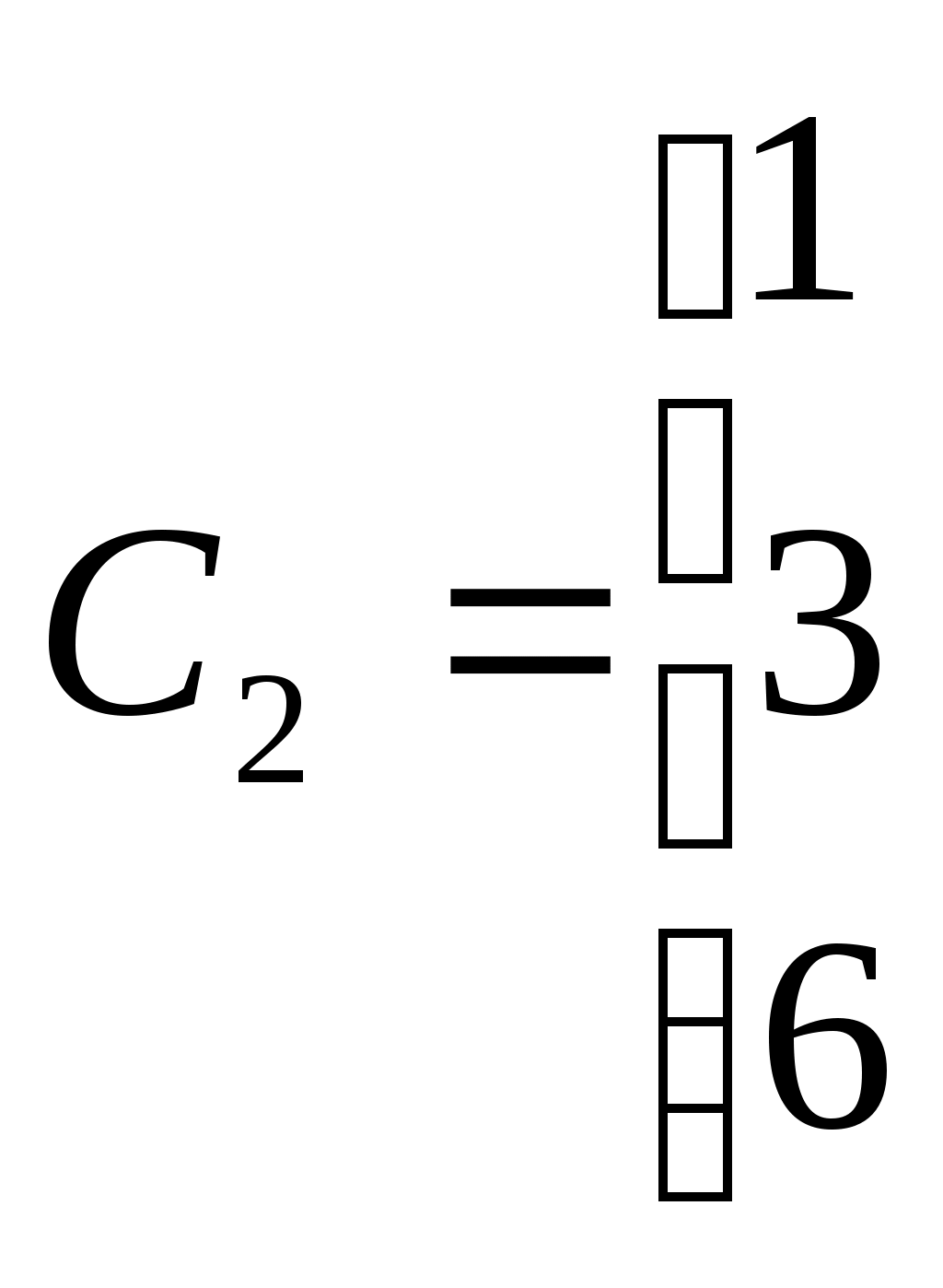


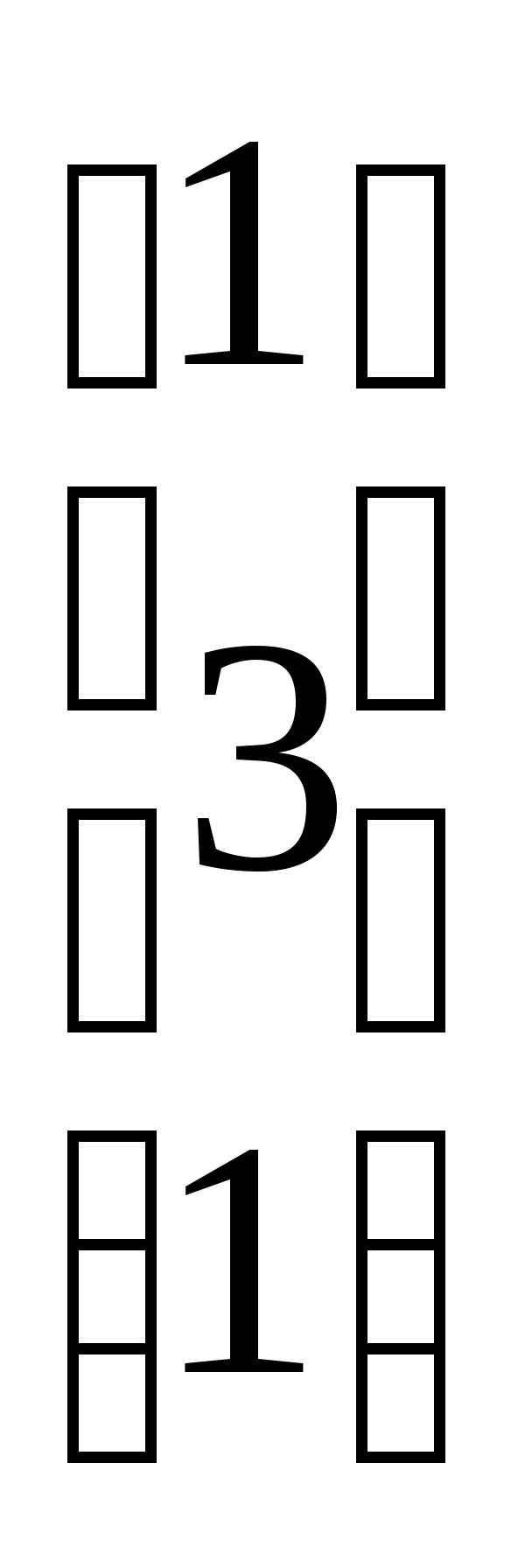 =
= 
4. Зашифрованное слово запишем в виде последовательности чисел 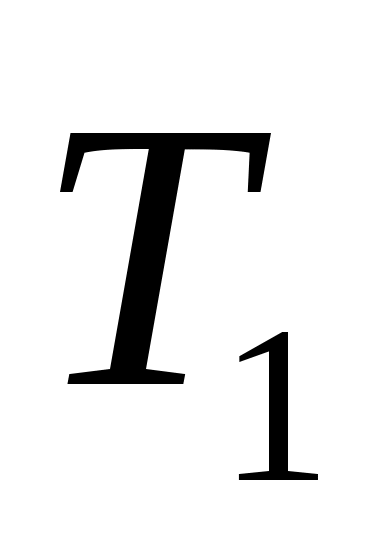 =<28,35,67,21,26,38>.
=<28,35,67,21,26,38>.
Задача 2.3. Расшифровать текст, полученный в задаче 2.2.
Решение.
1.Вычисляется определитель 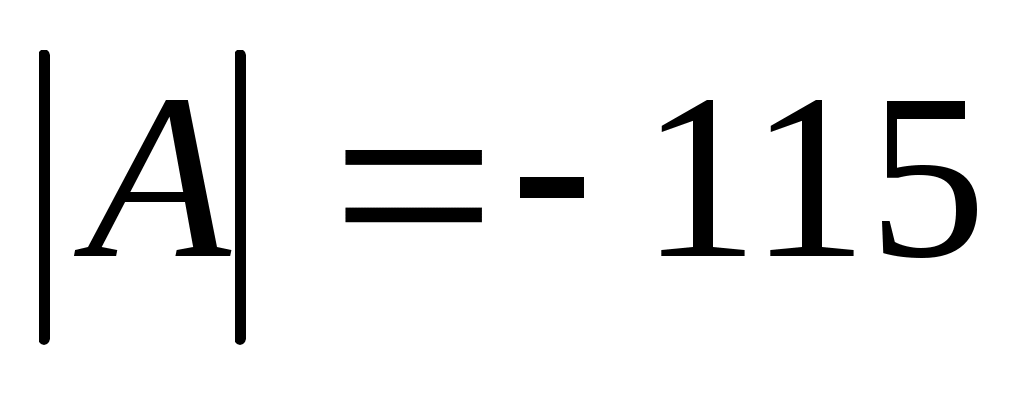 .
.
2.Определяется присоединённая матрица  , каждый элемент которой является алгебраическим дополнением элемента
, каждый элемент которой является алгебраическим дополнением элемента  матрицы А:
матрицы А:
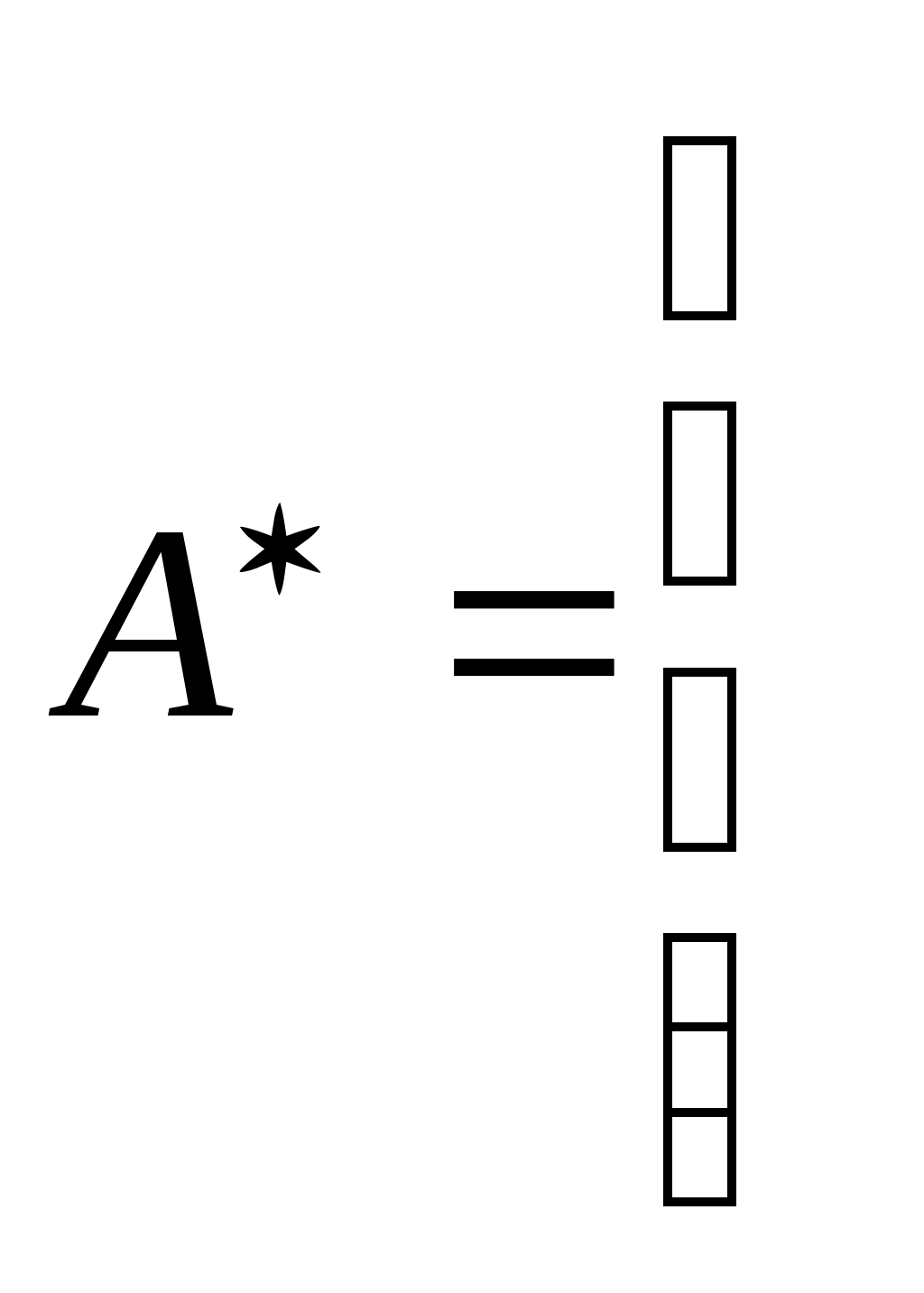
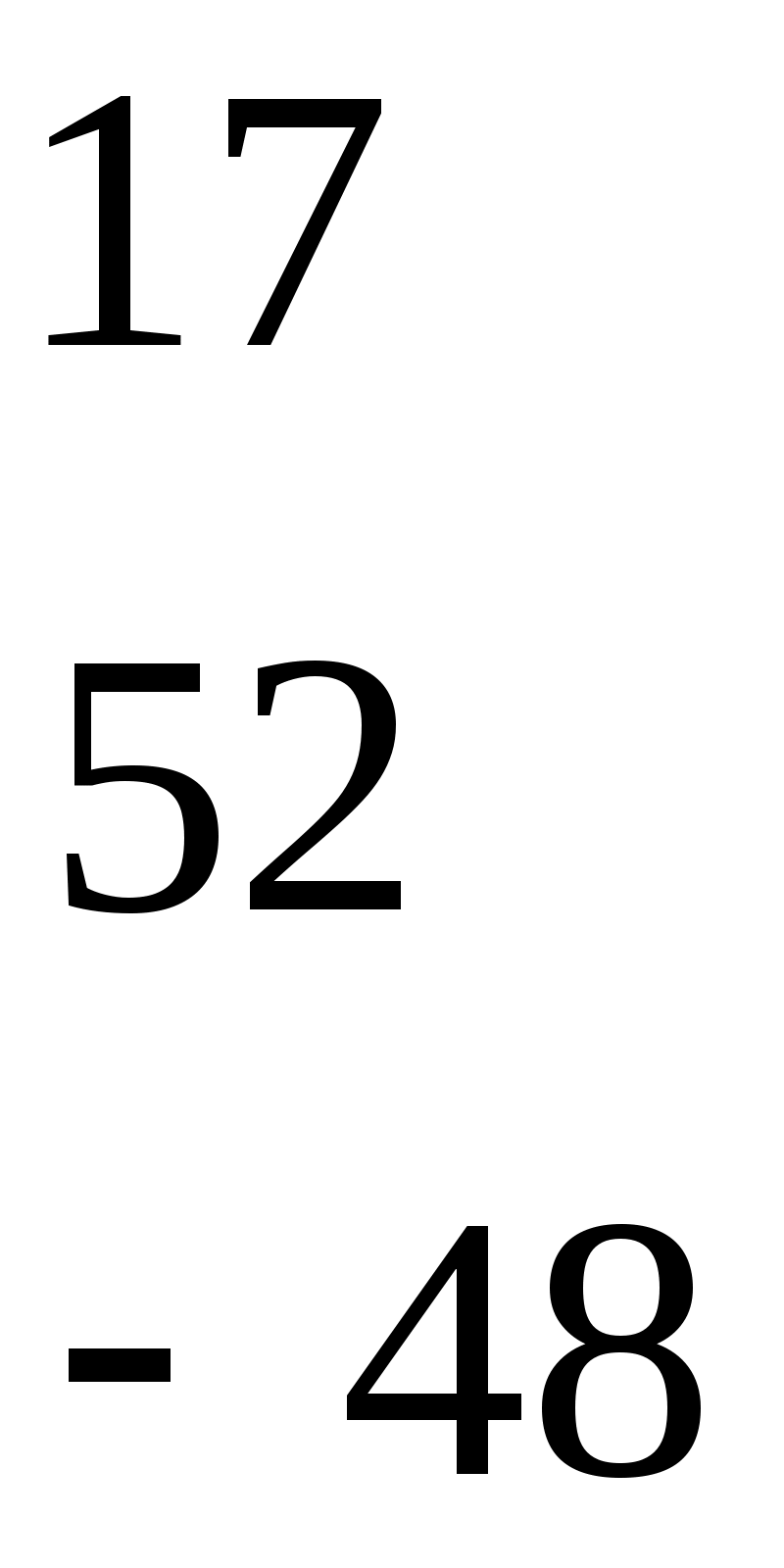
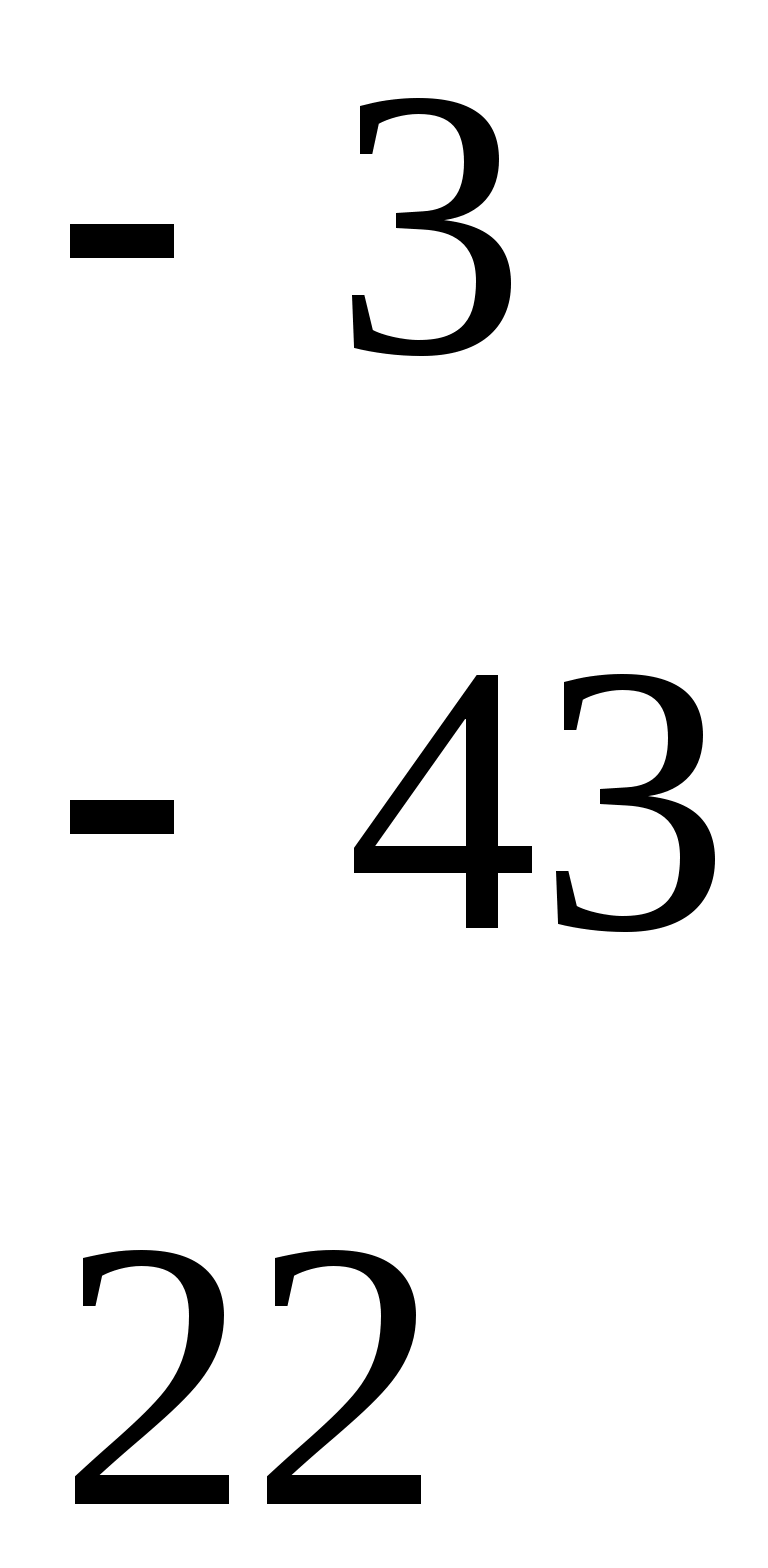
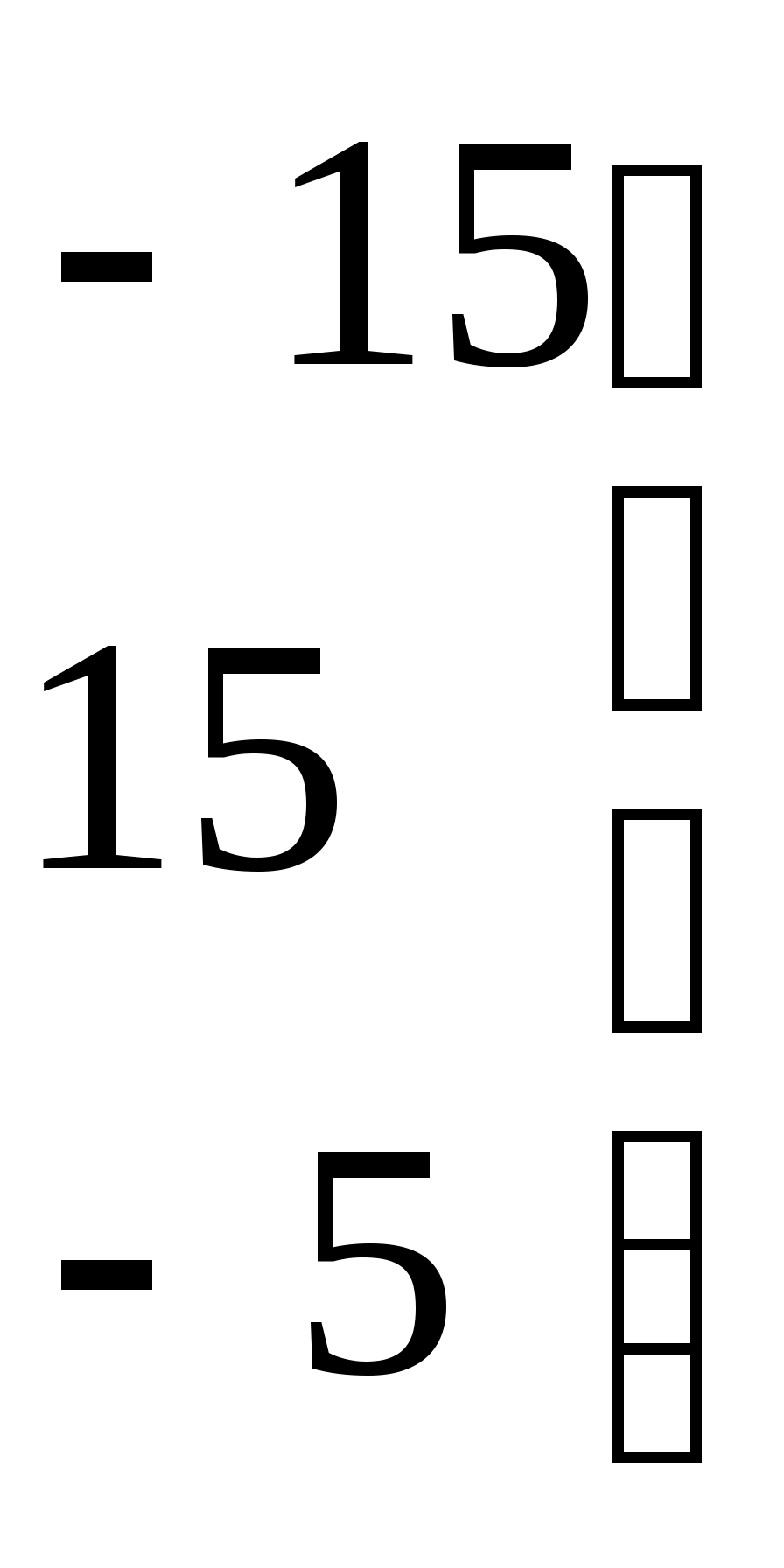
3.Получается транспонированная матрица 
 =
=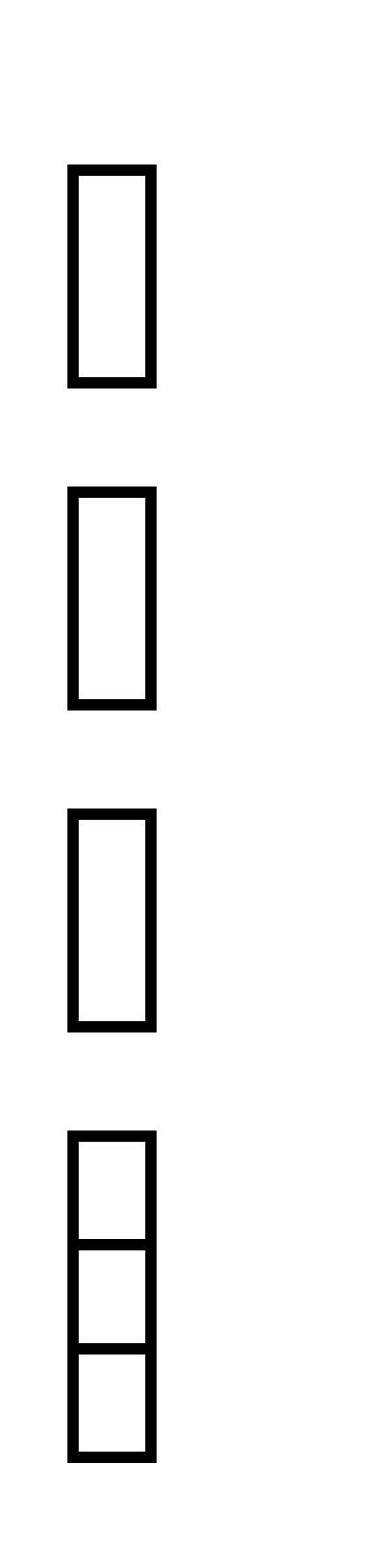
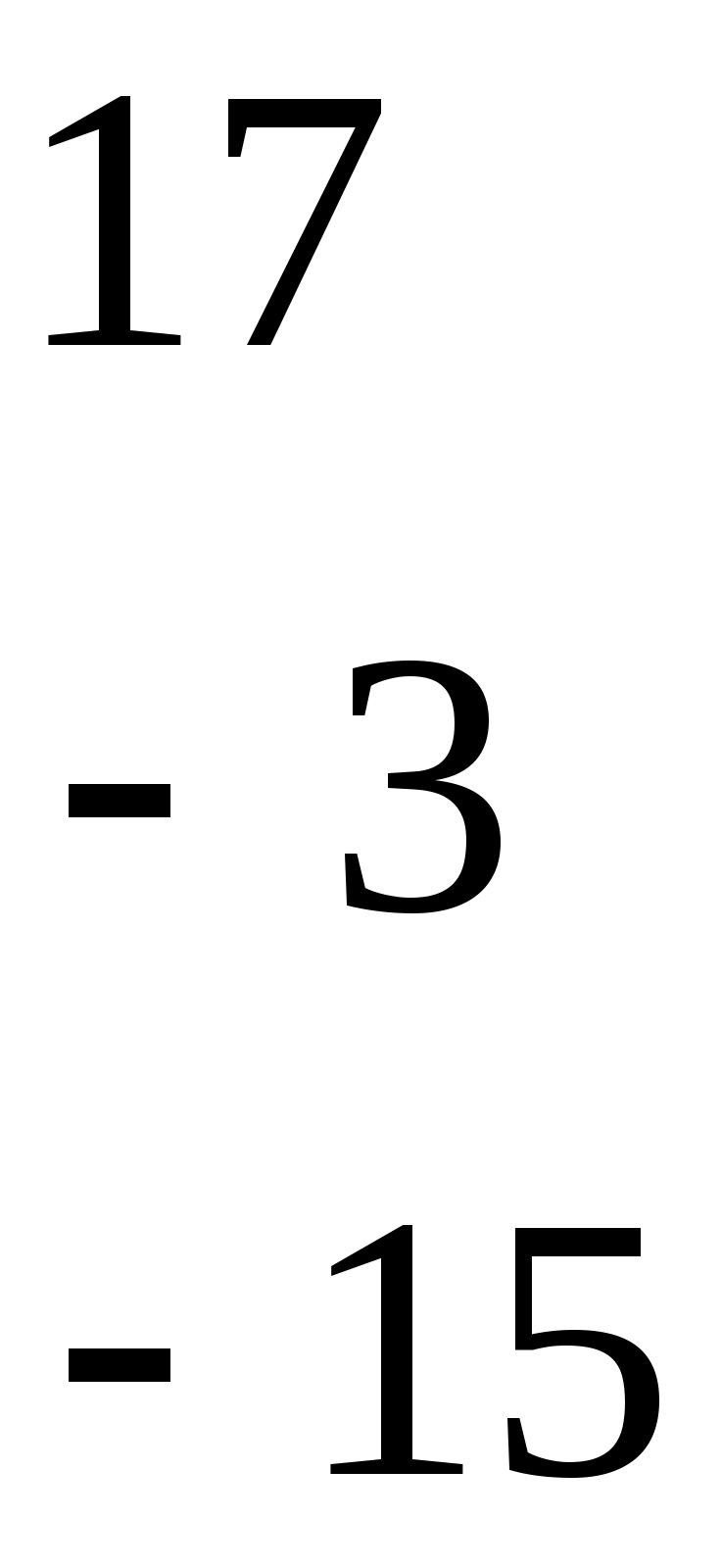
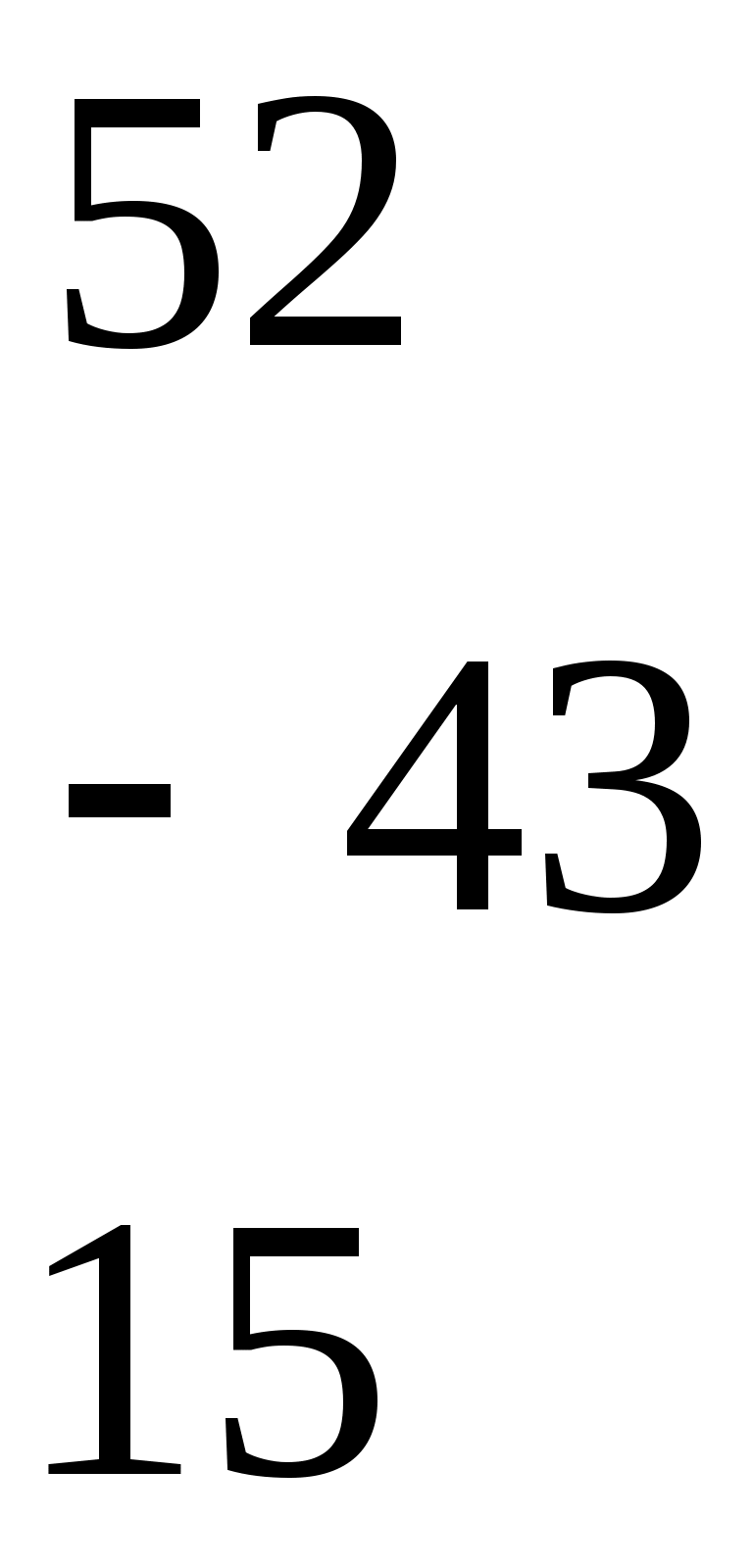
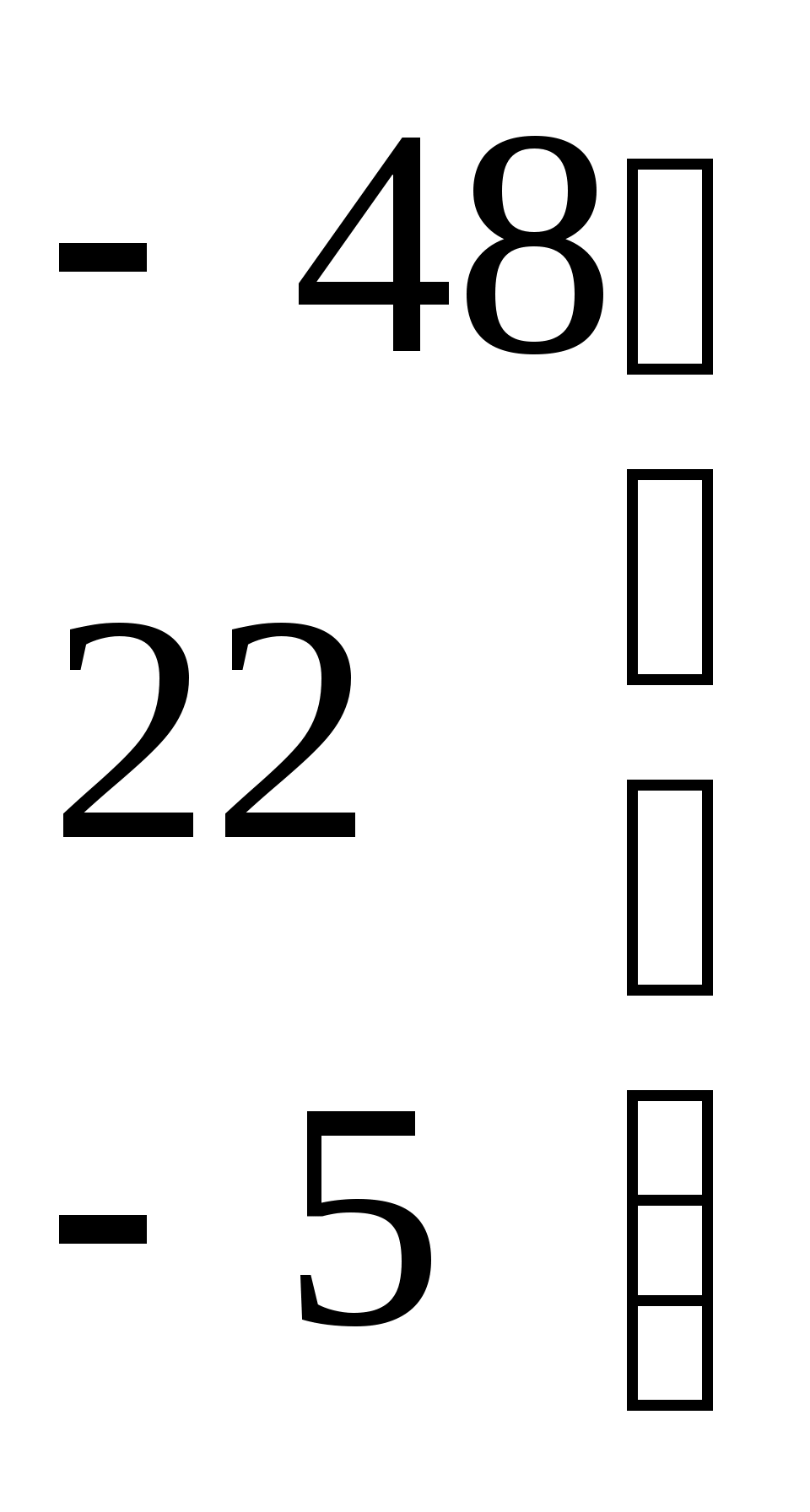
4.Вычисляется обратная матрица 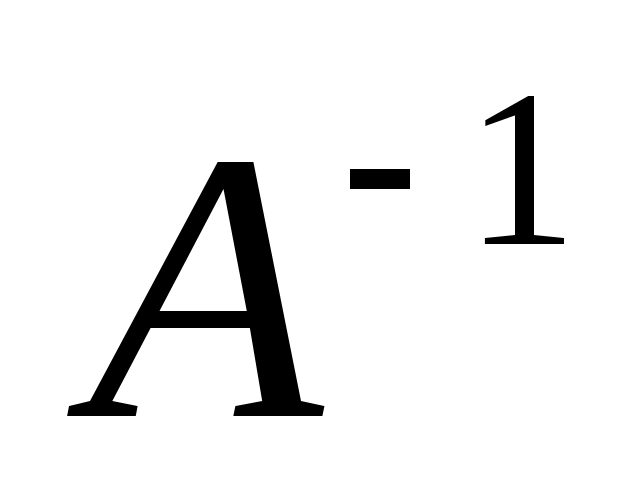 по формуле:
по формуле:
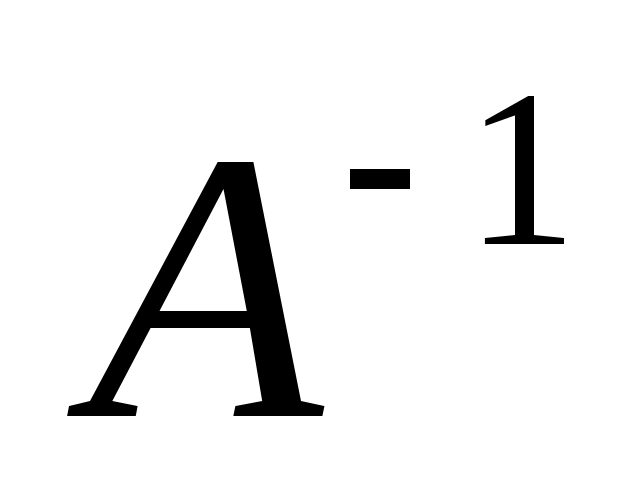 =
= ,
,
В результате вычислений обратная матрица имеет вид:
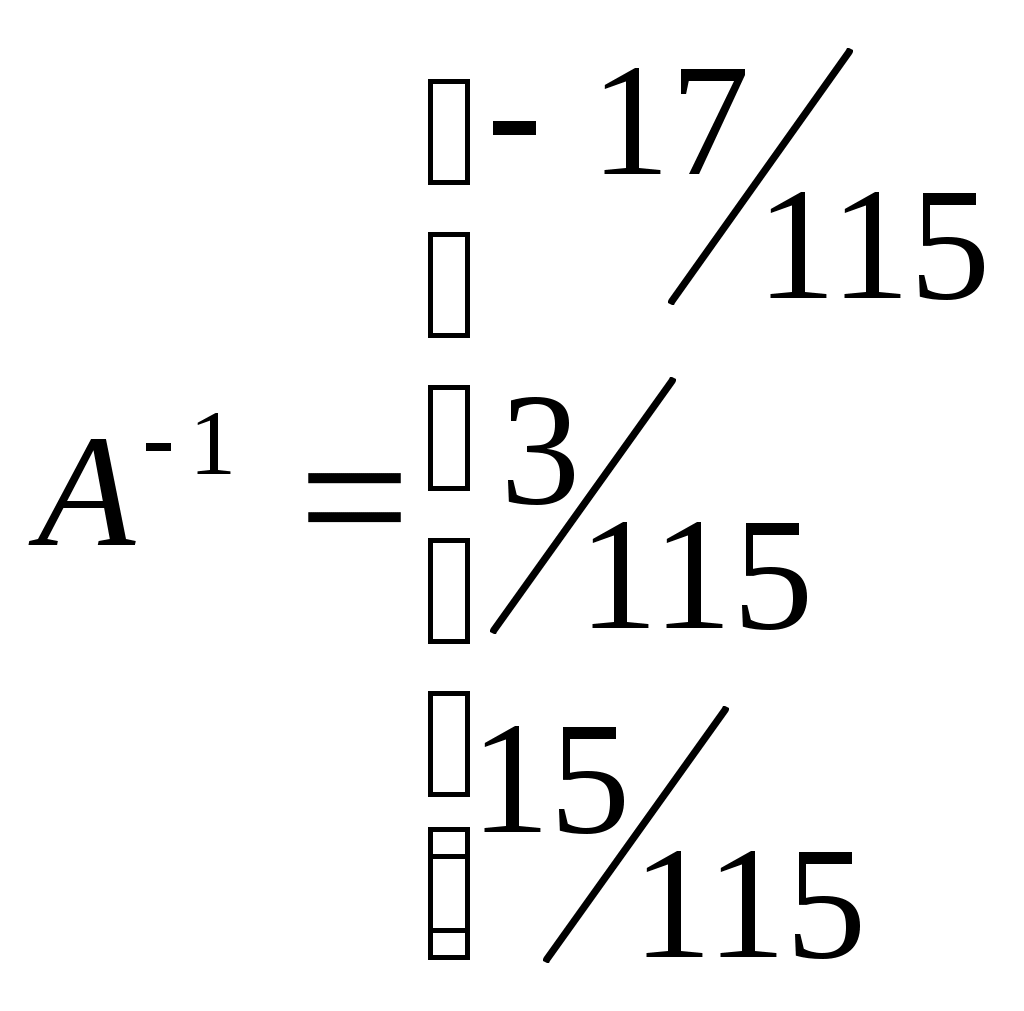
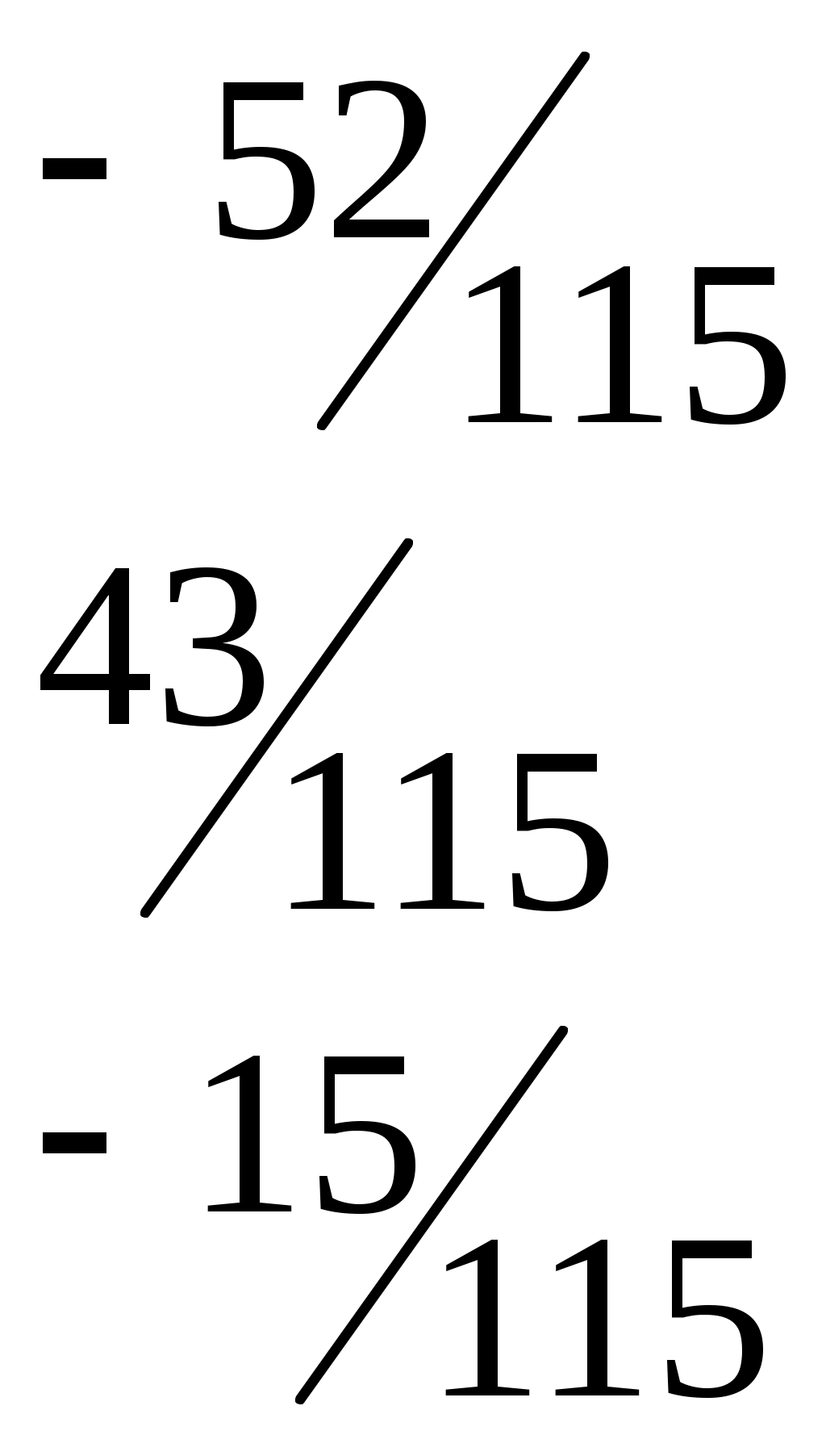
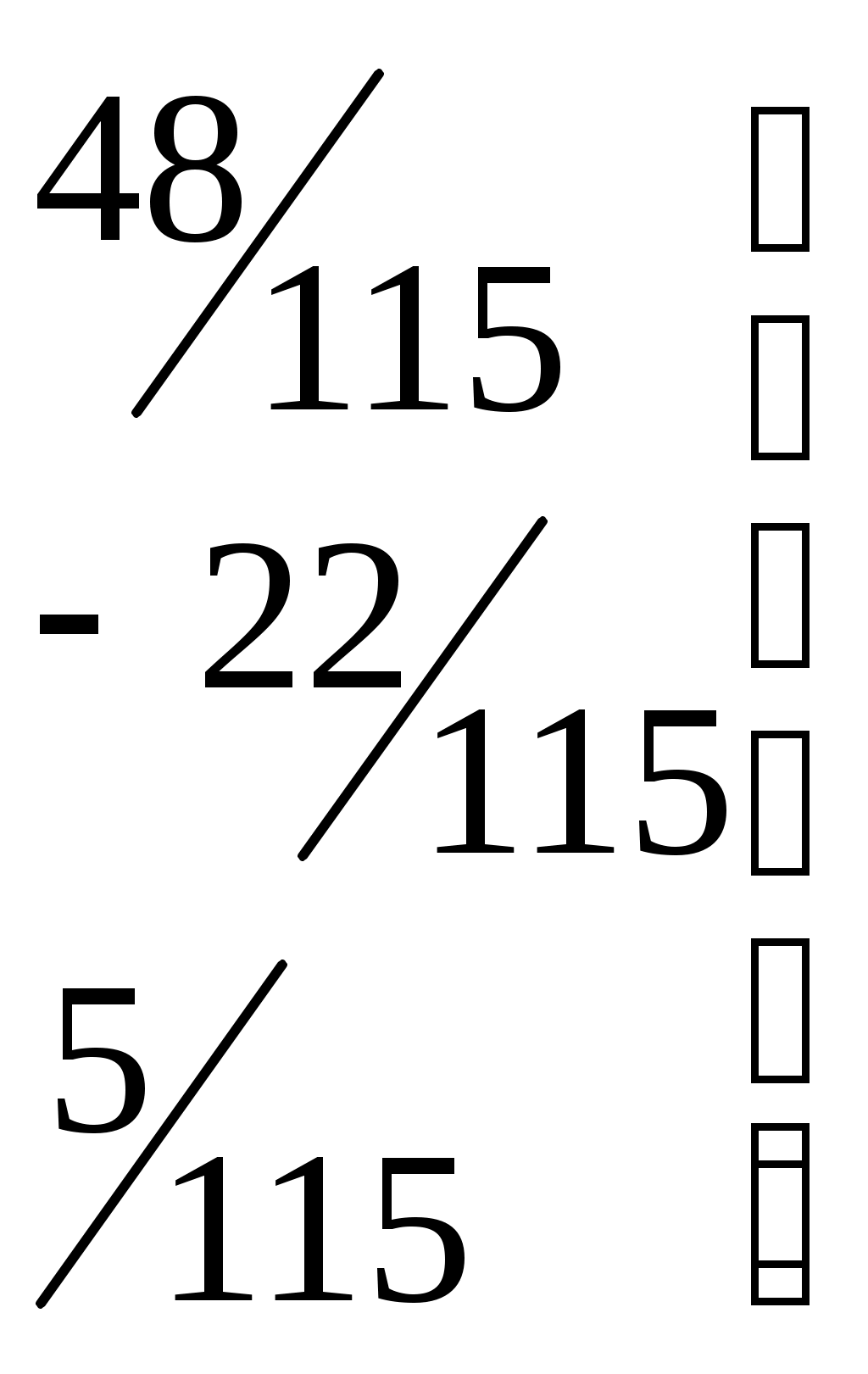
5.Определяются векторы 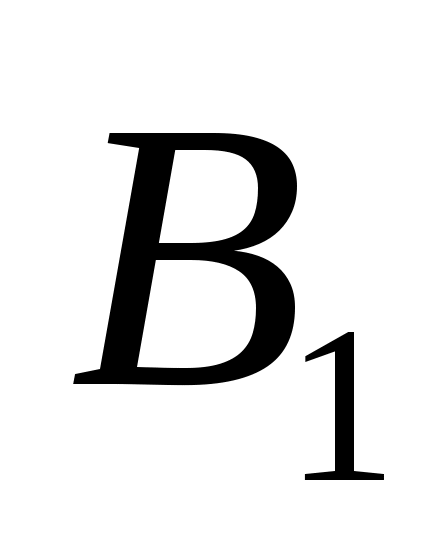 и
и 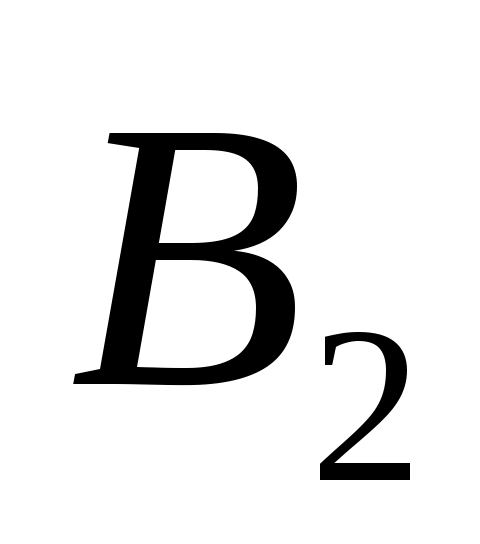 :
:
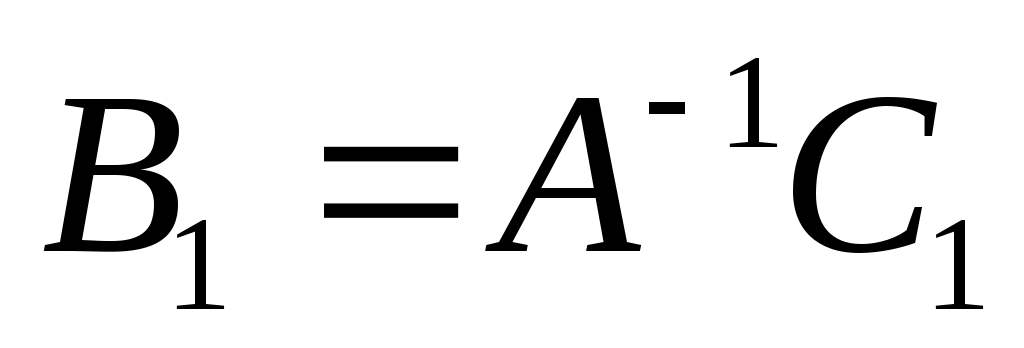 ;
; 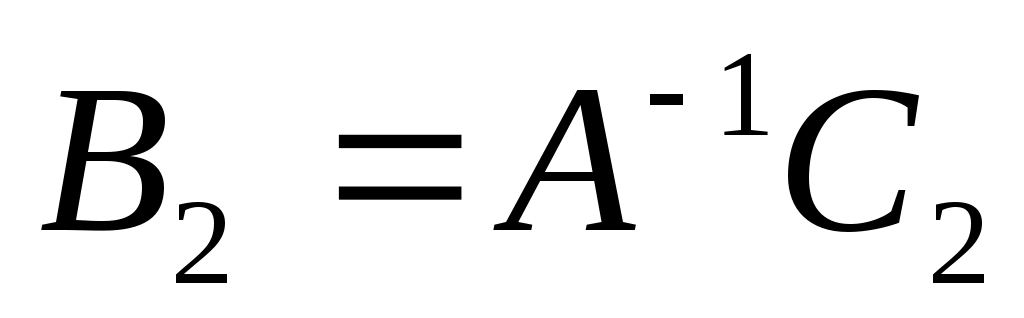
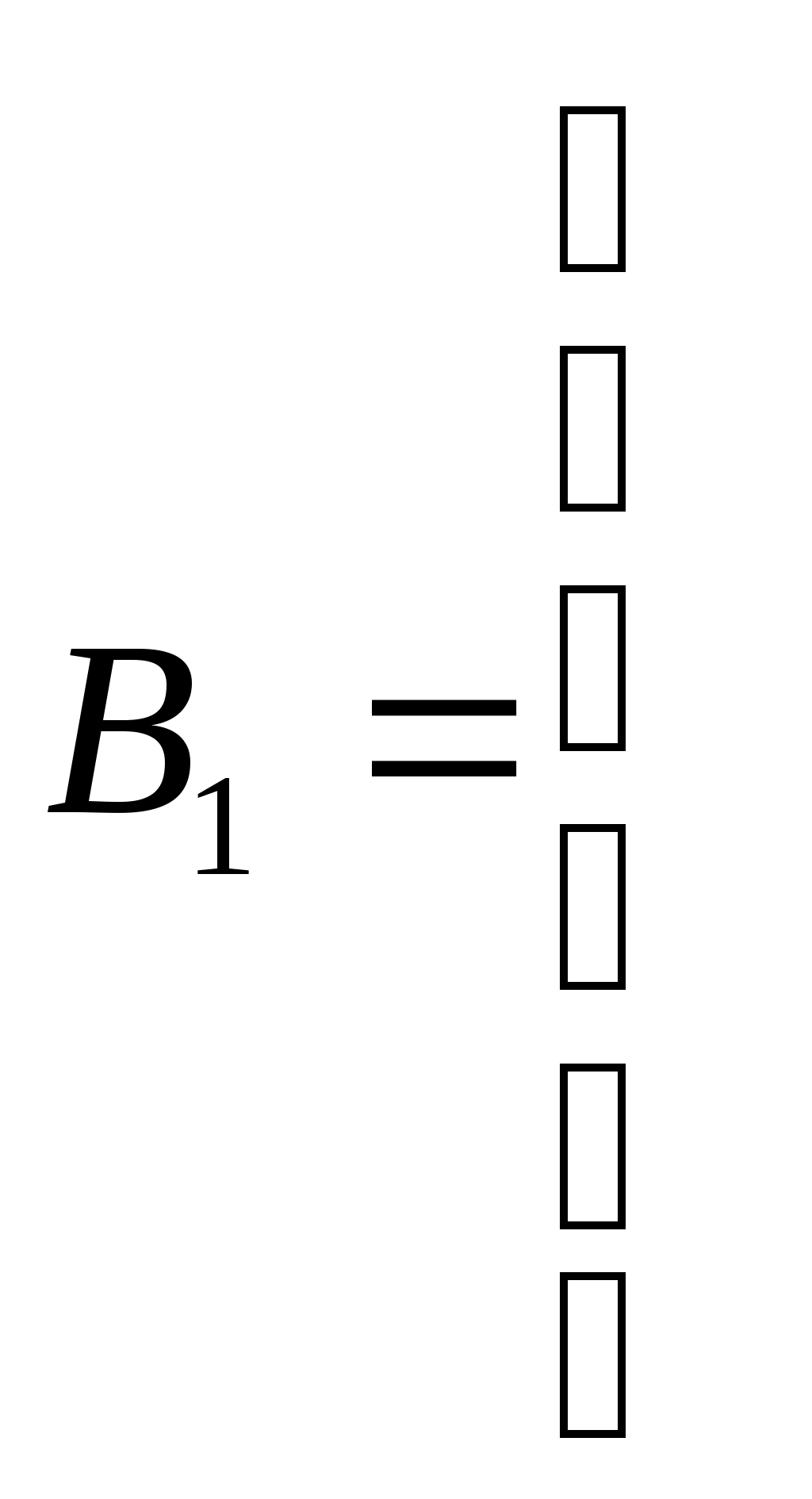
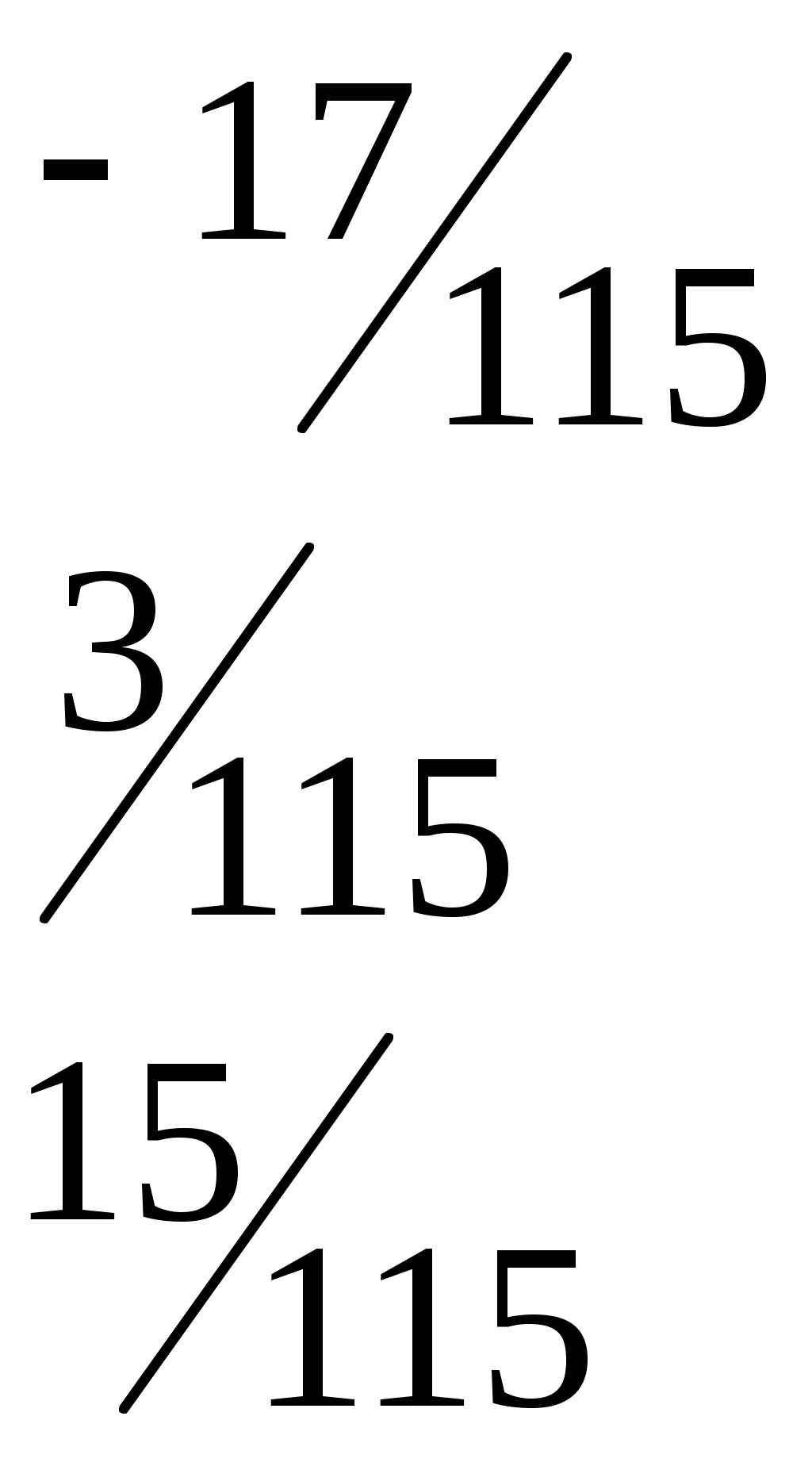
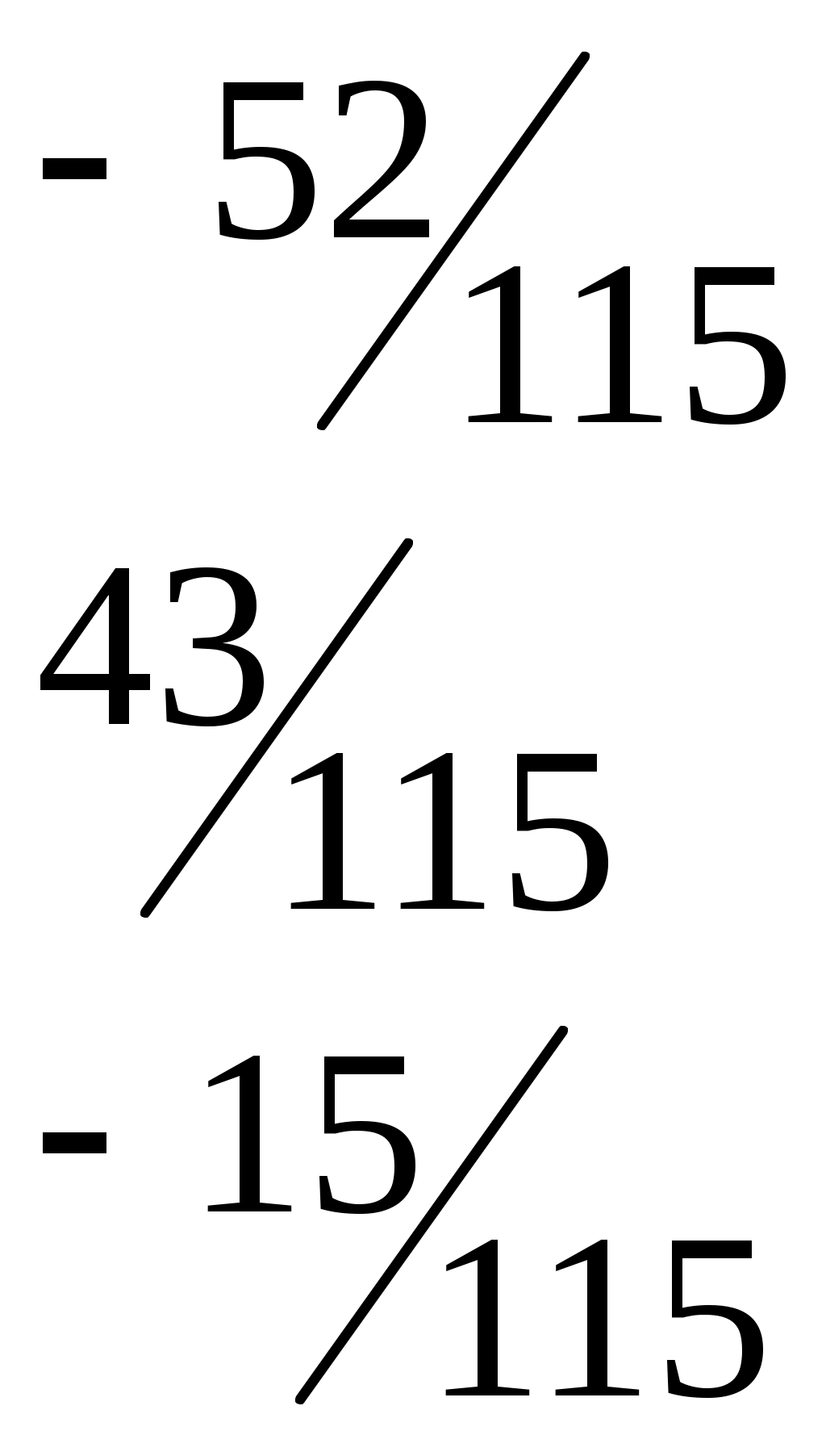
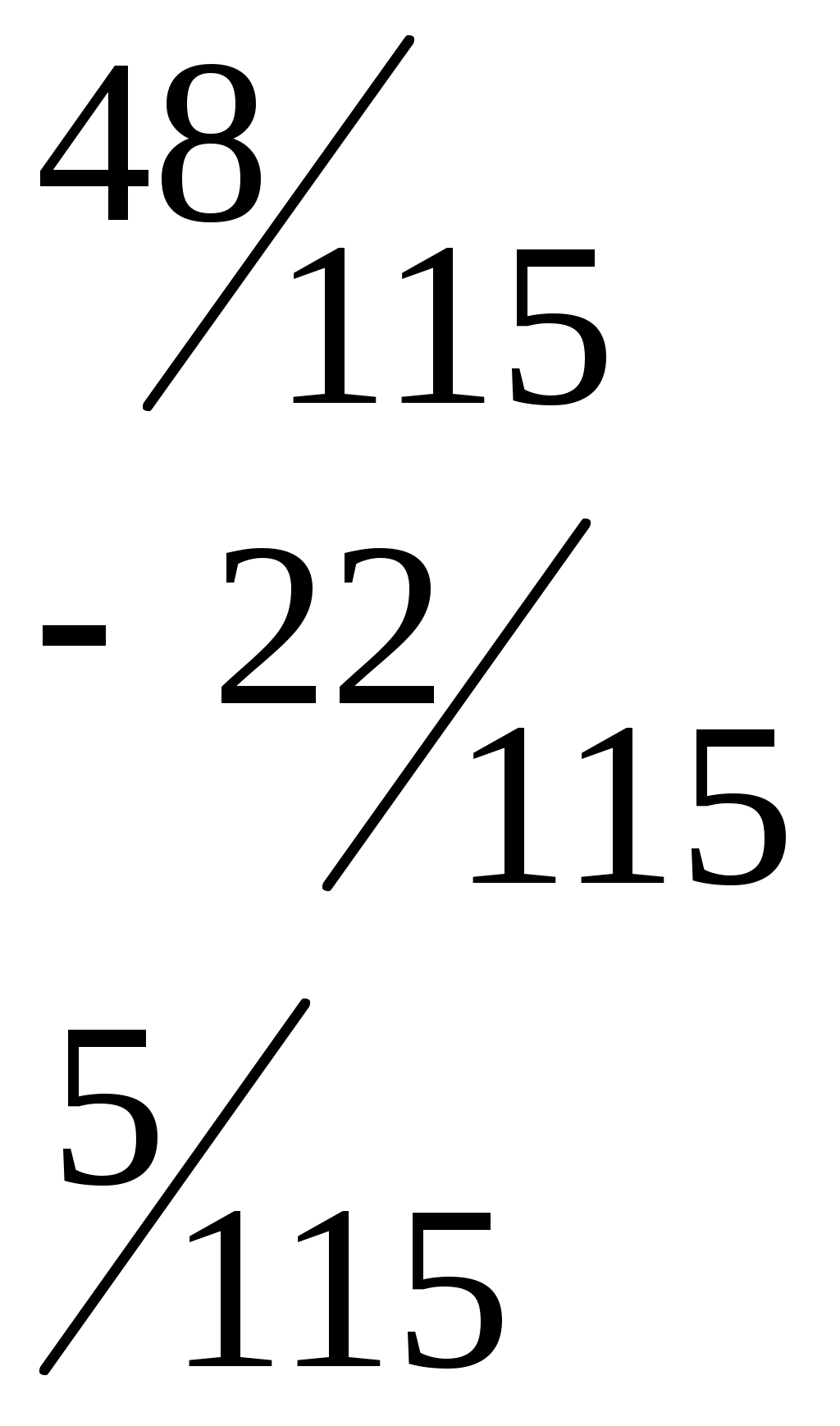
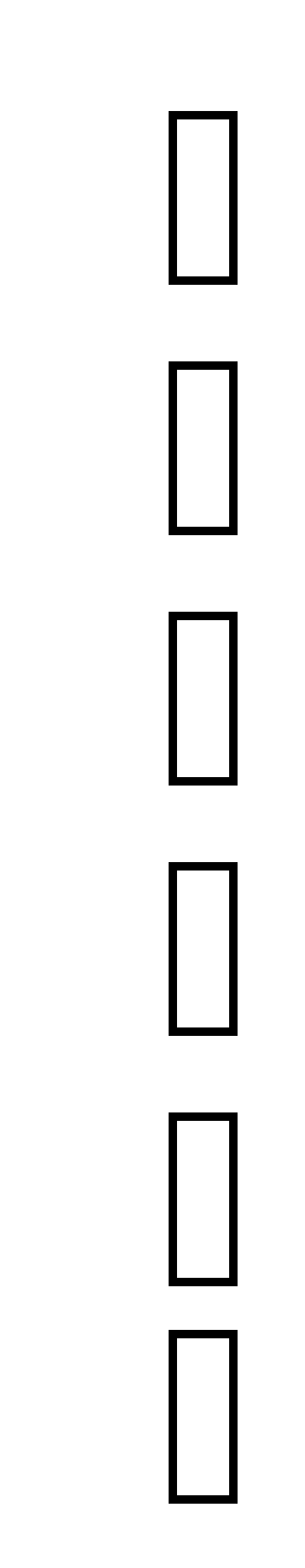
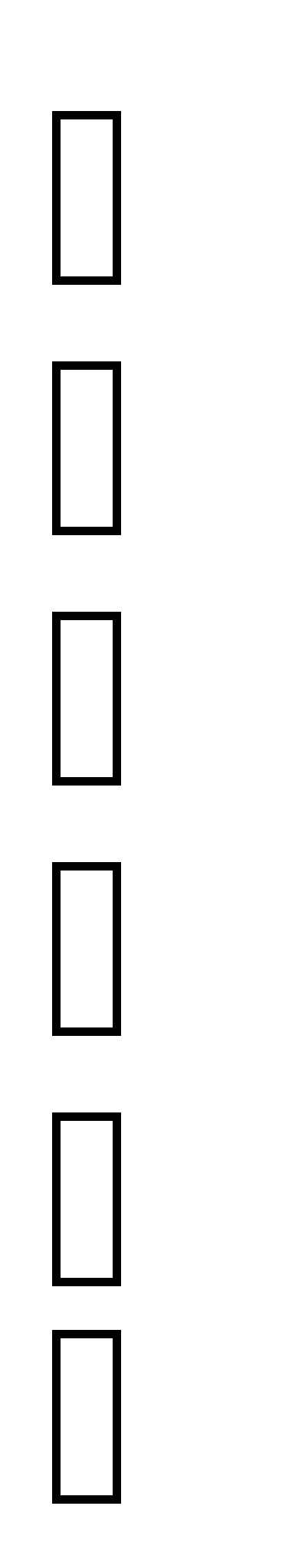
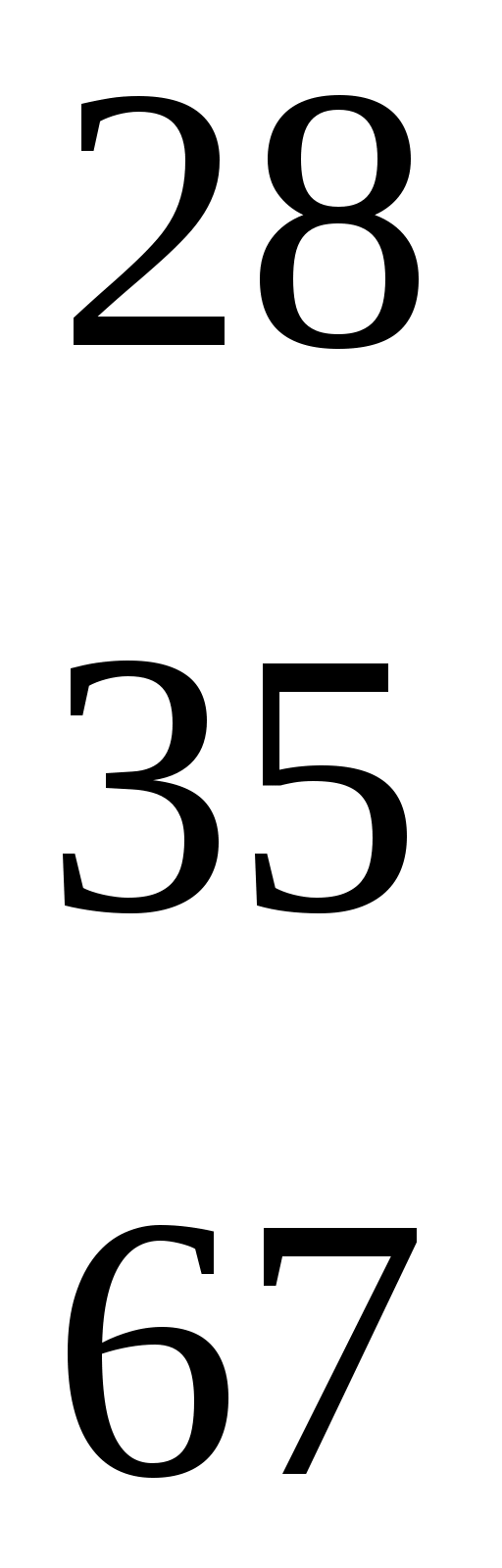
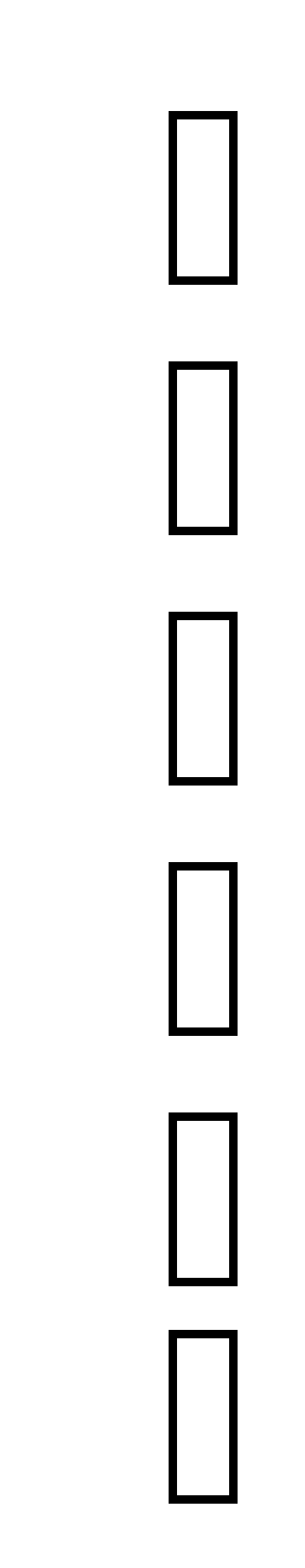 =
= 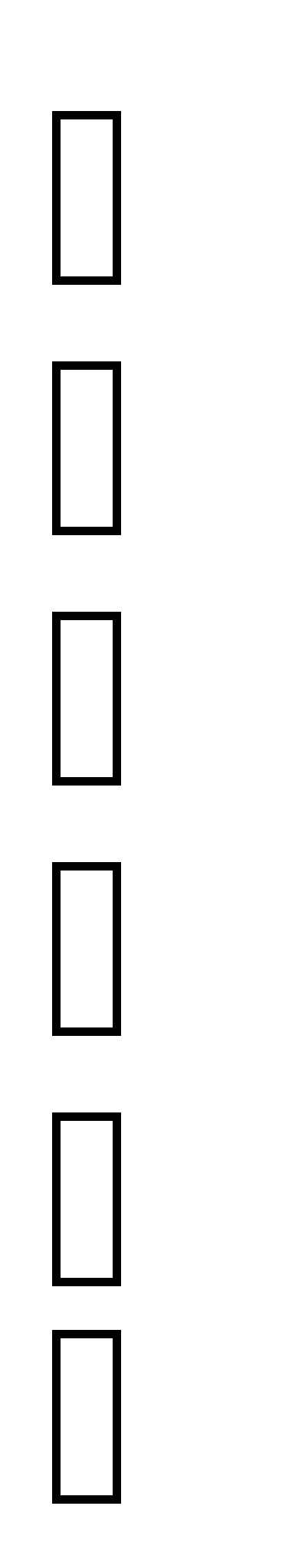
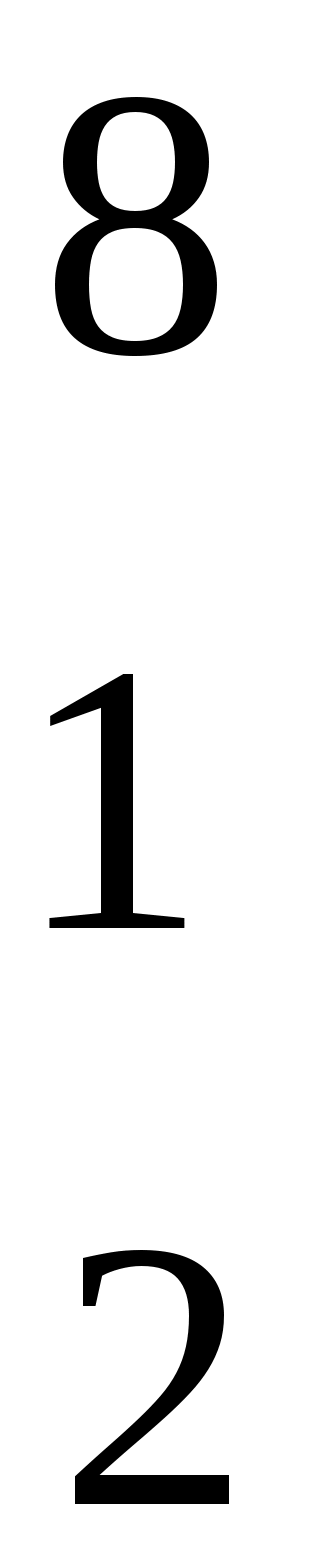
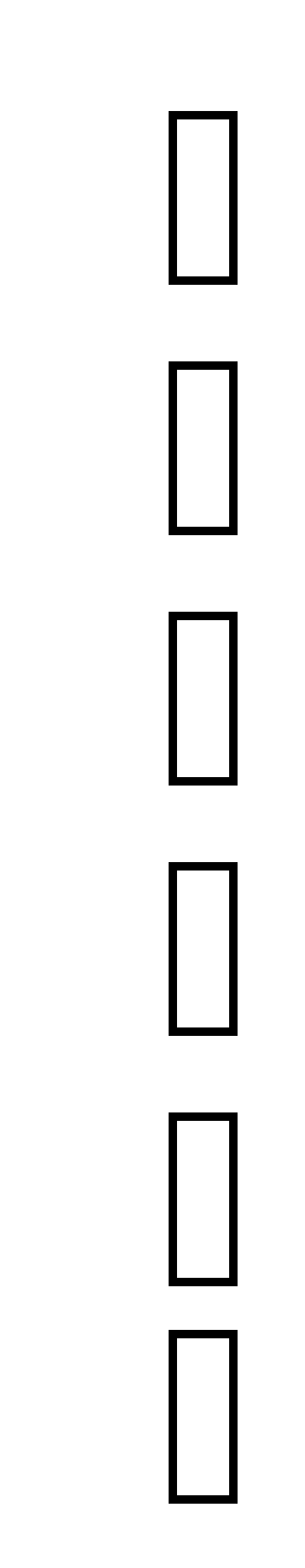

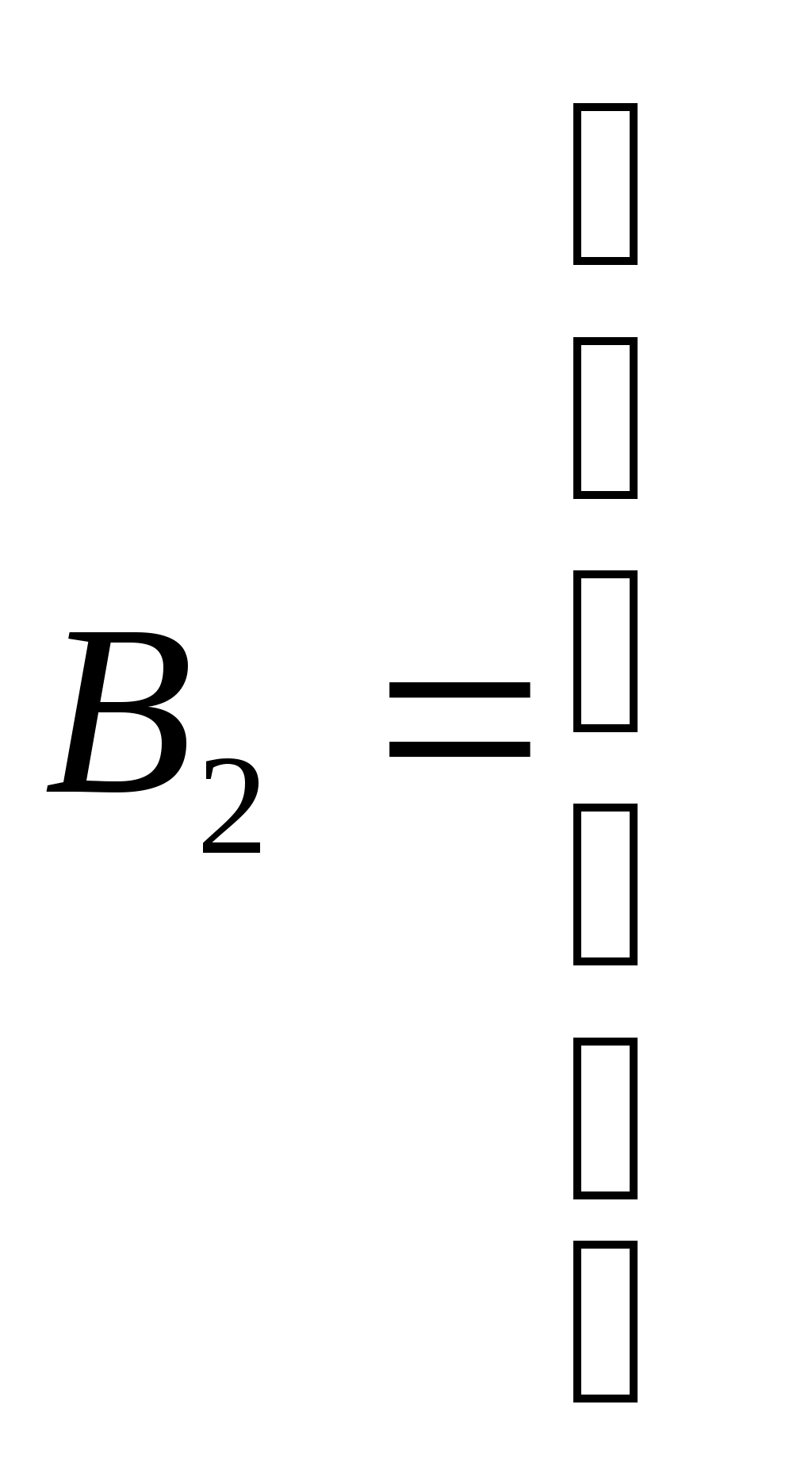
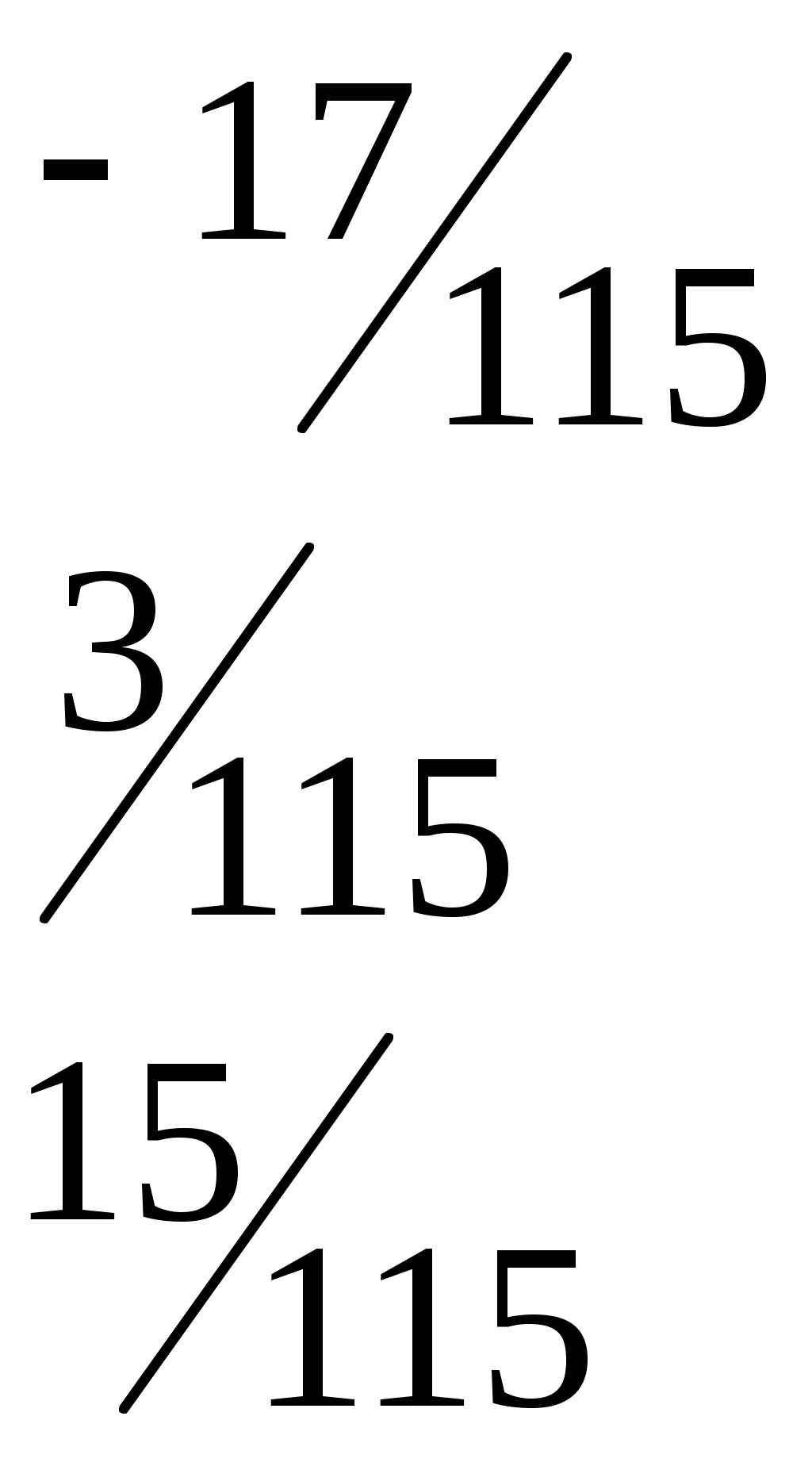
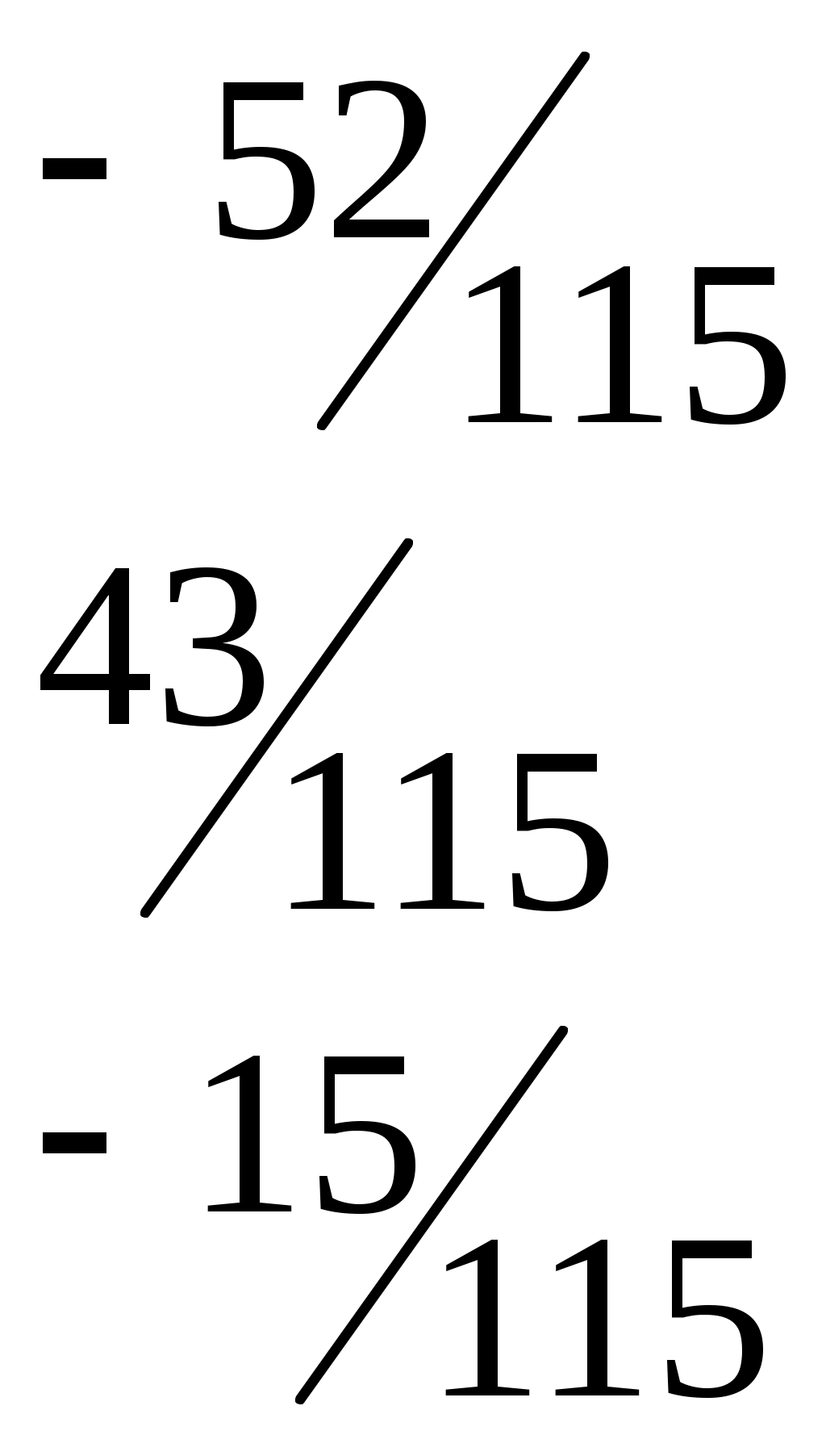
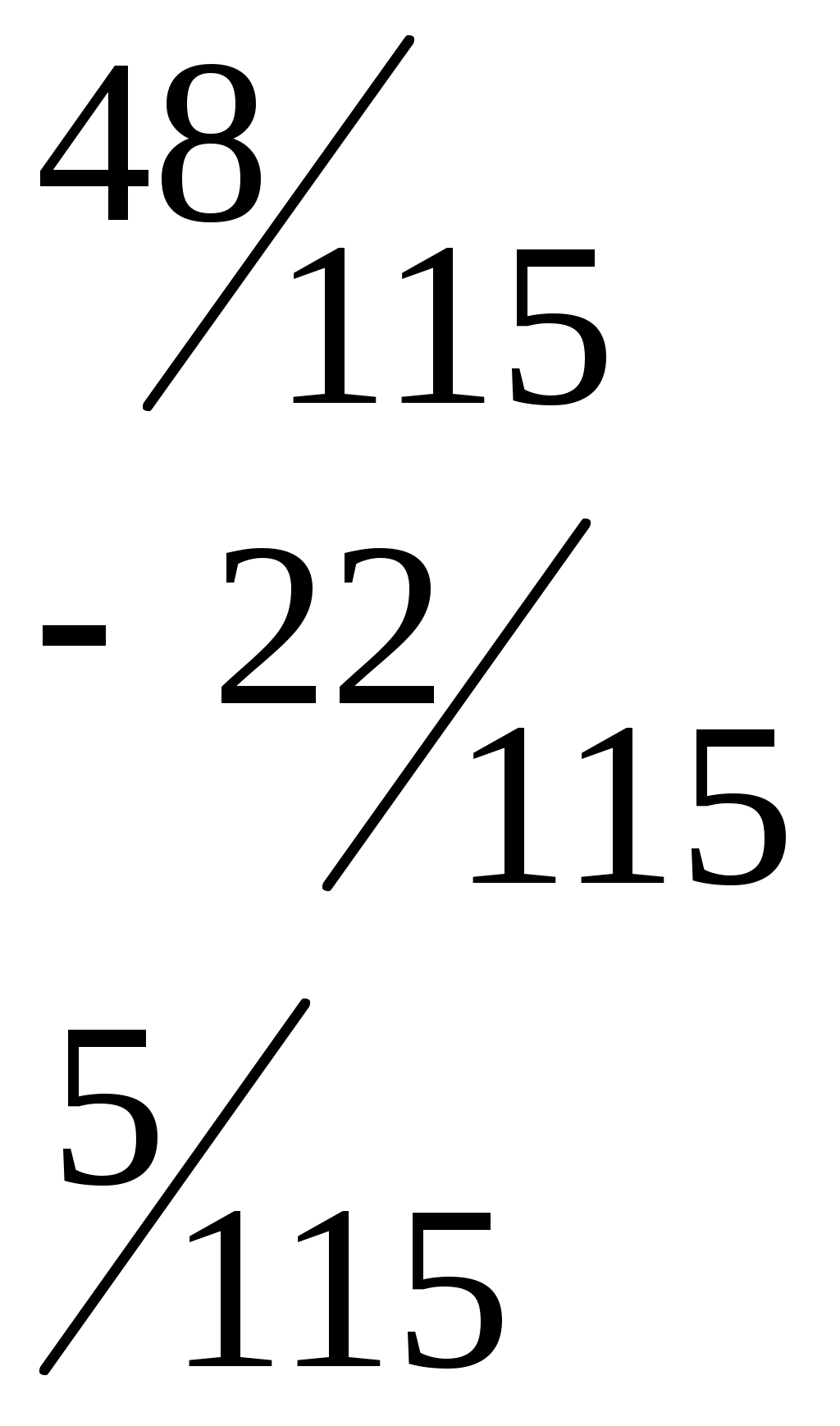
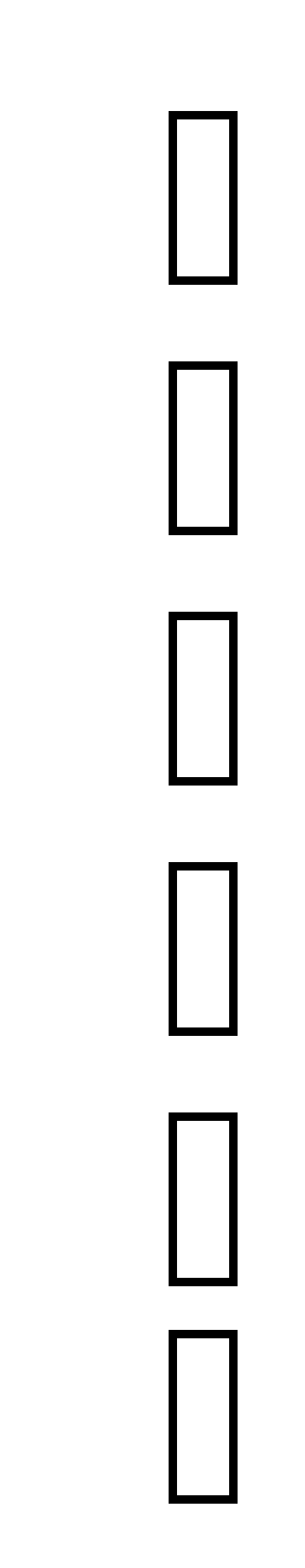
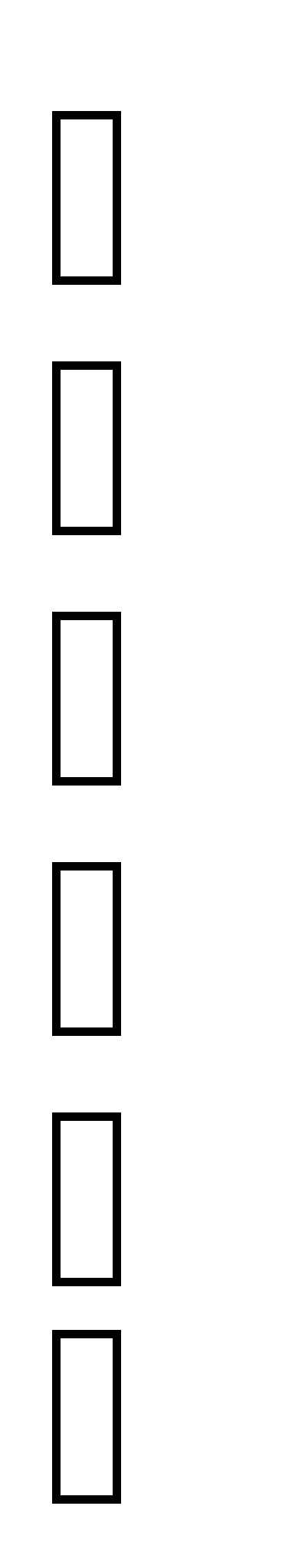
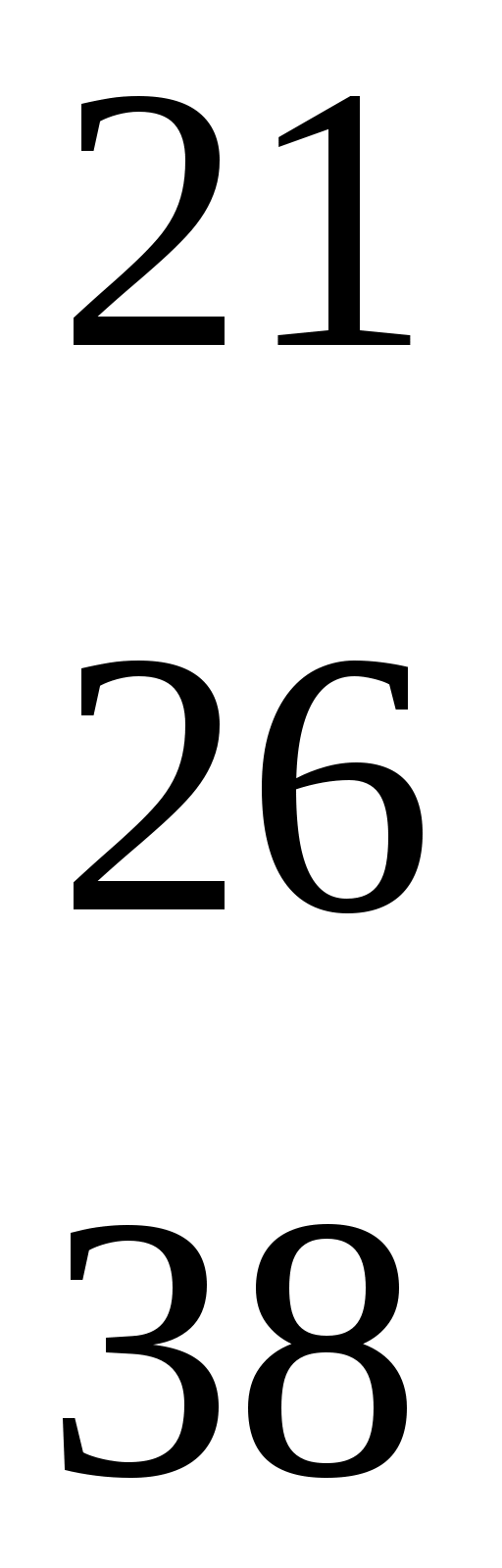
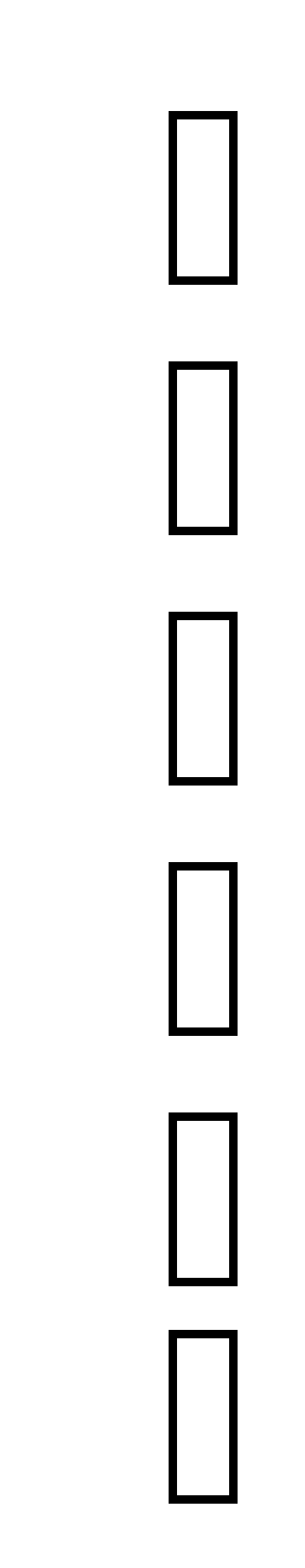 =
= 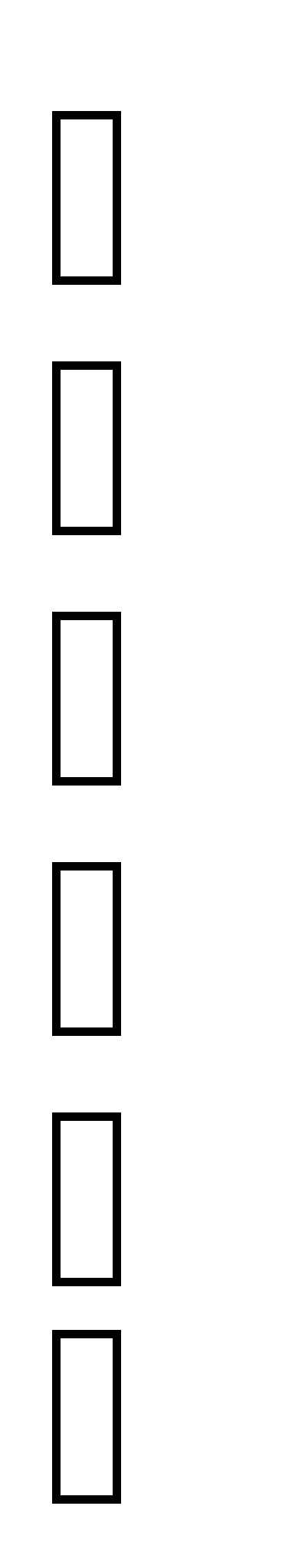
6.Получаем числовой эквивалент расшифрованного слова:
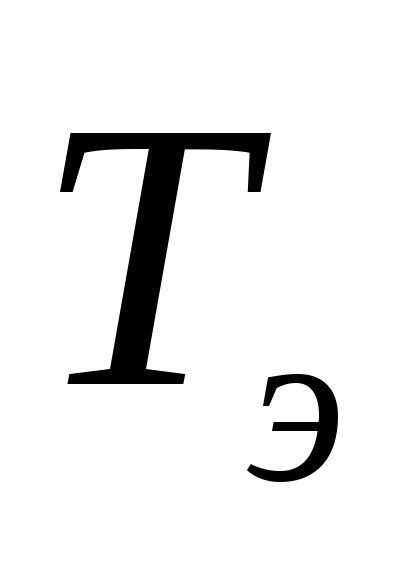 =<8,1,2,1,3,1>, который заменяется символами, в результате получается исходное слово
=<8,1,2,1,3,1>, который заменяется символами, в результате получается исходное слово
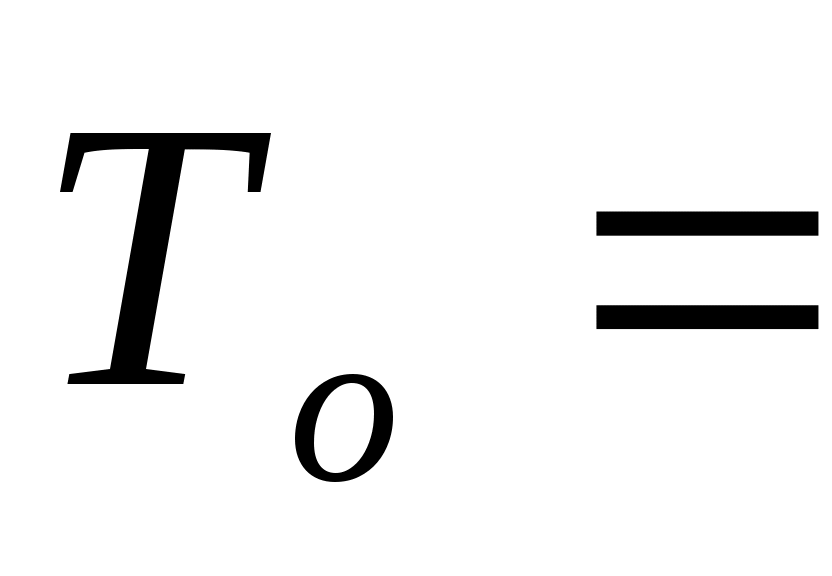 <ЗАБАВА>
<ЗАБАВА>
Пояснение к заданию 3
Асимметричная криптосистема RSA.
Расширенный алгоритм Евклида
-
Выбирают два больших простых числа pиq. Для большей криптостойкости pиqвыбирают равной длины.
-
Вычисляют произведение: n=pq
-
Вычисляют z=(p-1)(q-1) и выбирают число е взаимно простое с z, т.е. НОД (е,z)=1.
-
Для вычисления закрытого (секретного) ключа d решается сравнение
еd 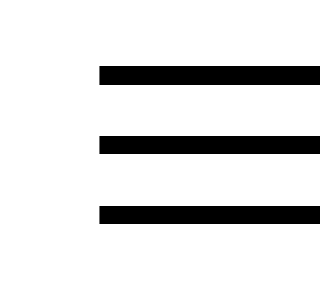 1modz (1)
1modz (1)
Решение (1) имеет вид 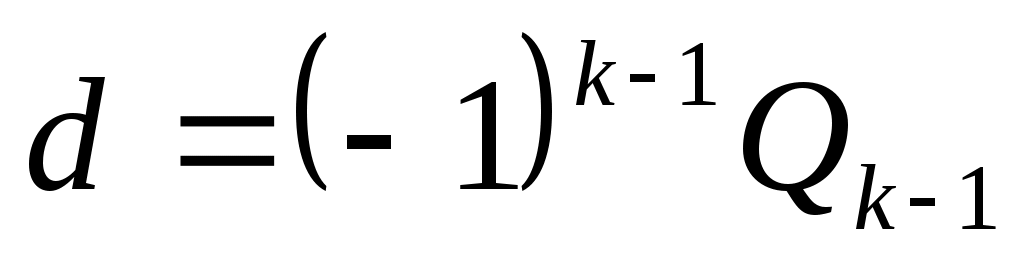
Для вычисления ключа dвоспользуемся расширенным алгоритмом Евклида. Для этого число 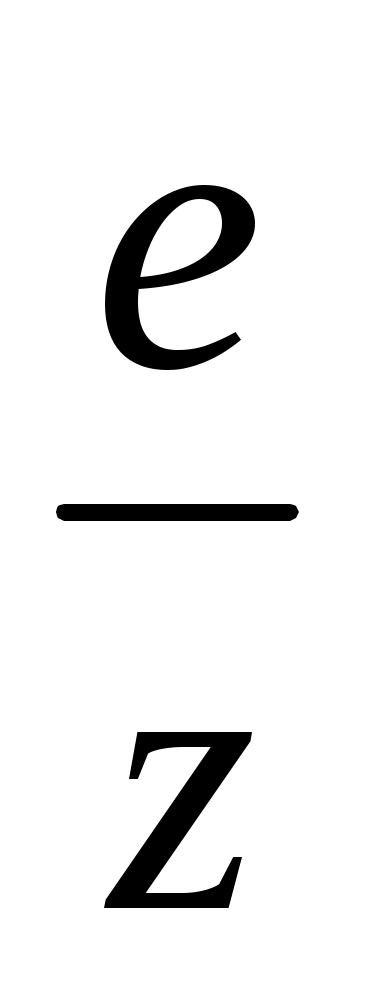 обращается в конечную цепную дробь:
обращается в конечную цепную дробь:
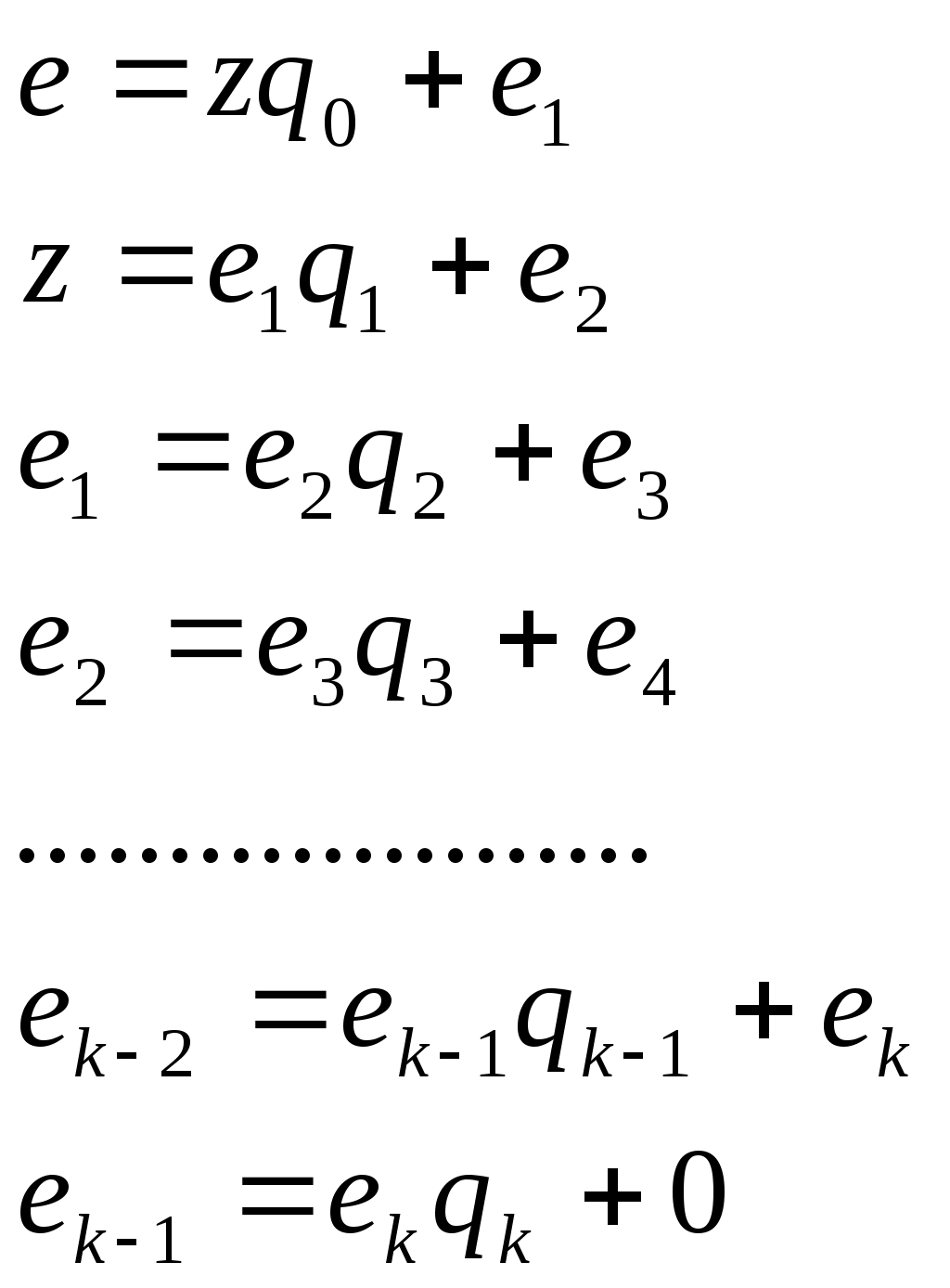
Цепная дробь имеет вид: 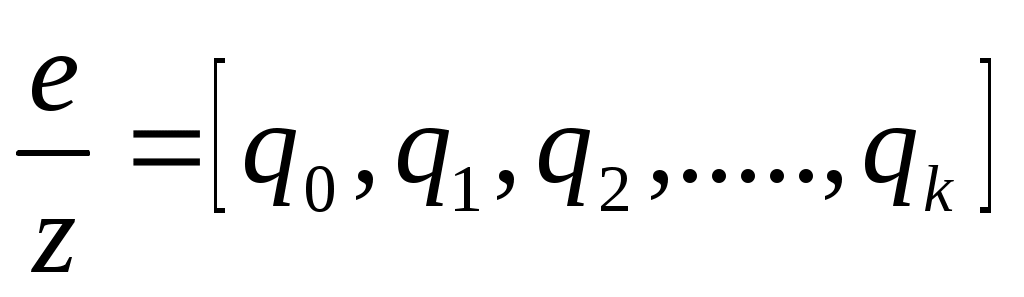 , а последовательности
, а последовательности 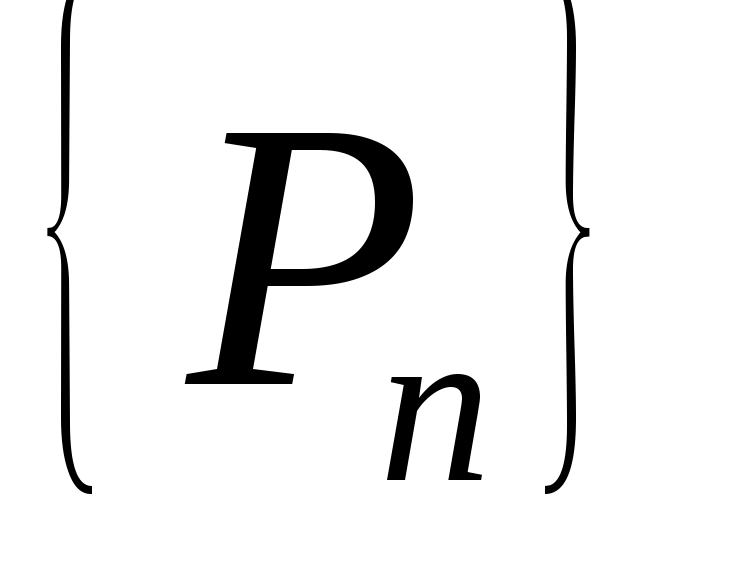 и
и 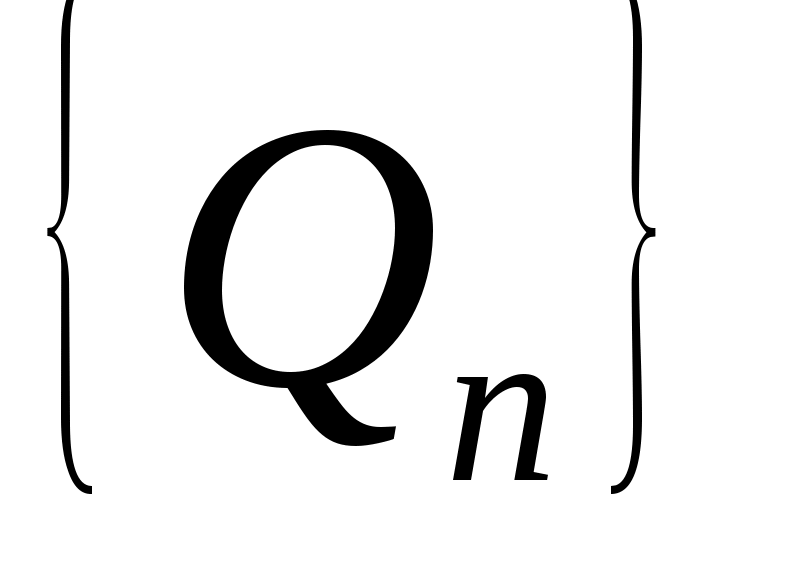 числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:
числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:
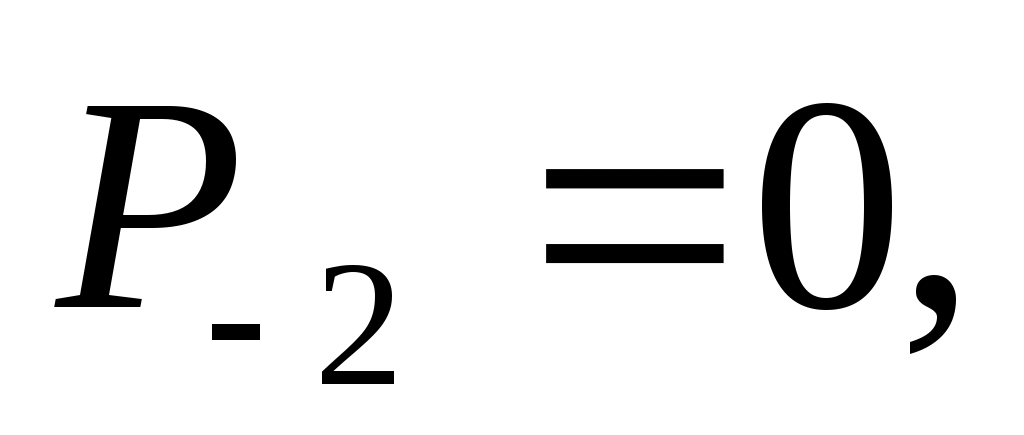
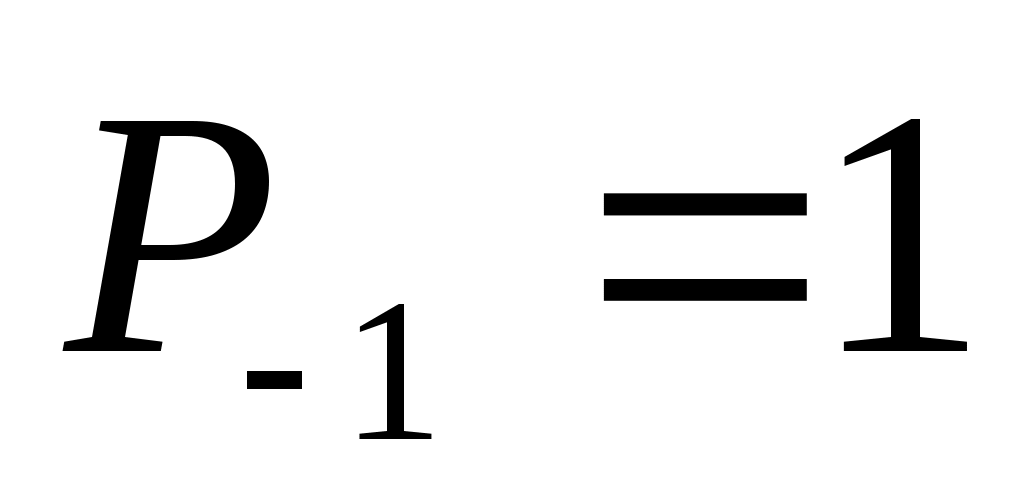 ,
, 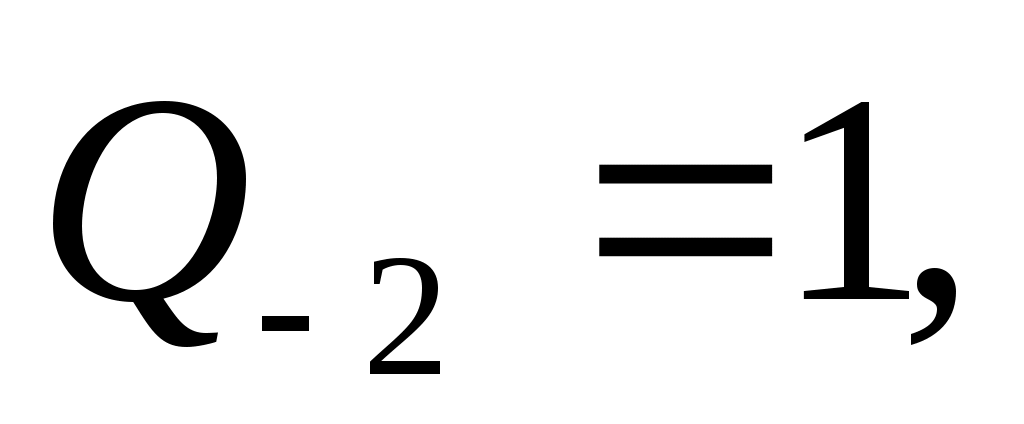
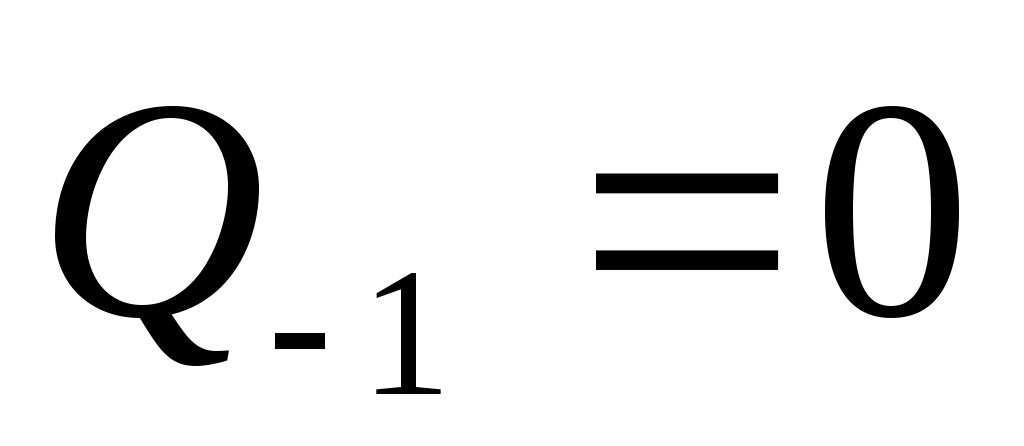 .
.
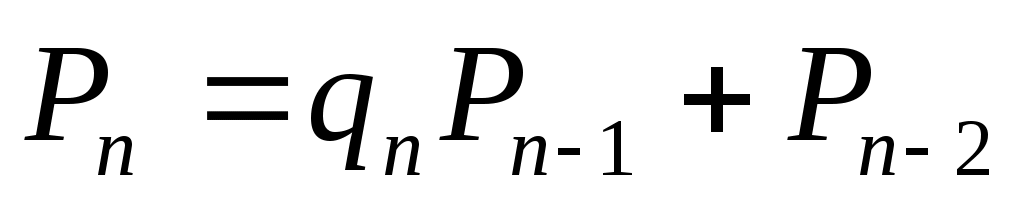 ,
, 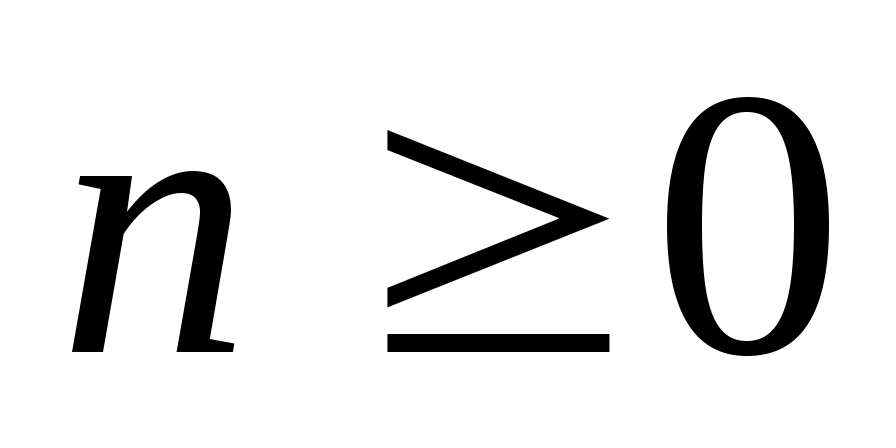
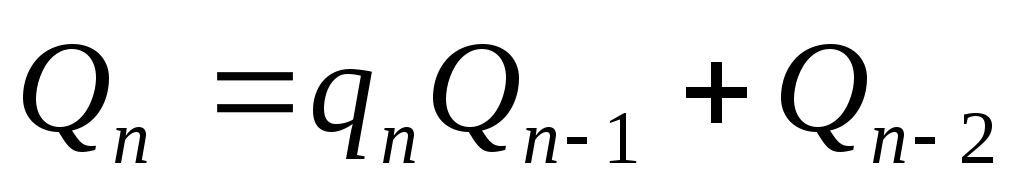 ,
, 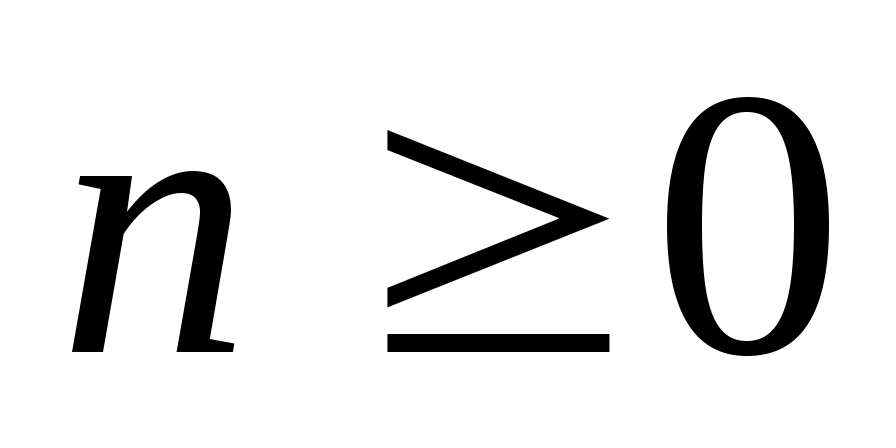
Их вычисления удобно оформить в виде таблицы:
1.3.5. Биграммный шифр Плейфейра
Шифр Плейфейра, изобретенный в 1854 г., является наиболее известным биграммным шифром замены. Он применялся Великобританией во время первой мировой войны. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.
Для удобства запоминания шифрующей таблицы отправителем и получателем сообщений можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей таблицей Трисемуса из предыдущей задачи ( рис. 1.5).
Процедура шифрования включает следующие шаги.
-
Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок. -
Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
2а.Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы А и Й в табл. на рис.2.6), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это – буквы АЙОВ. Пара букв АЙ отображается в пару ОВ. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста.)
2б.Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в.Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.)
Задача 1.10. Зашифровать биграммным шифром Плейфера текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Решение.Разобьём этот текст на биграммы:
ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы (рис. 1.5) в следующую последовательность биграмм шифртекста
ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ
При дешифровании применяется обратный порядок действий.
Шифрование биграммами резко повышает стойкость шифров к вскрытию. Хотя книга И.Трисемуса "Полиграфия" была относительно доступной, описанные в ней идеи получили признание лишь спустя три столетия. По всей вероятности, это было обусловлено плохой осведомленностью криптографов о работах богослова и библиофила Трисемуса в области криптографии.
Пояснение к заданию 2
Методы шифрования
2.1. Метод перестановок на основе маршрутов
Гамильтона
Этот метод реализуется путем выполнения следующих шагов.
Шаг 1. Исходный текст разбивается на блоки. Если длина шифруемого текста не кратна длине блока, то на свободные места последнего блока помещаются служебные символы-заполнители(например,*)
Шаг 2. Символами блока заполняется таблица, в которой для каждого порядкового номера символа в блоке отводится вполне определенное место (рис. 2.1).



Исходная
таблица
Маршрут 1
Маршрут 2
Рисунок 2.1 - Вариант 8-элементной таблицы и маршрутов
Гамильтона.
Шаг 3. Считывание символов из таблицы осуществляется по одному из маршрутов. Увеличение числа маршрутов повышает криптостойкость шифра. Маршруты выбирают либо последовательно, либо их очерёдность задаётся ключом К.
Шаг 4. Зашифрованная последовательность символов разбивается на блоки фиксированной длины L. Величина L может отличаться от длины блоков, на которые разбивается исходный текст на шаге 1.
Расшифрование производится в обратном порядке.
Задача 2.1. Требуется зашифровать текст
Решение. Воспользуемся вышеизложенной методикой построения шифра по шагам.
Шаг 1. Исходный текст разбивается на 3 блока:
Блок
Блок
Шаг 2. Заполняется 3 матрицы с маршрутами 2,1,1 (рис.2.2.)


Маршрут 2

Маршрут 1
Маршрут 1
Рисунок 2.2 - Шифрование с помощью маршрутов Гамильтона.
Шаг 3. Получение шифртекста путём расстановки символов в соответствии с маршрутами.
Шаг4. Разбиение на блоки шифртекста
Возможно применение и других маршрутов.
2.2. Аналитические методы шифрования
Среди аналитических методов наибольшее распространение получили методы, основанные на использовании матриц. Зашифрование К-го блока исходной информации, представленного в виде вектора
Расшифрование информации осуществляется путём последовательного перемножения векторов
Задача 2.2. Требуется зашифровать слово
A=
Решение.
1.Определим числовой эквивалент исходного слова как последовательность соответствующих порядковых номеров букв слова
2.Разобьём
3. Умножим матрицу А на векторы
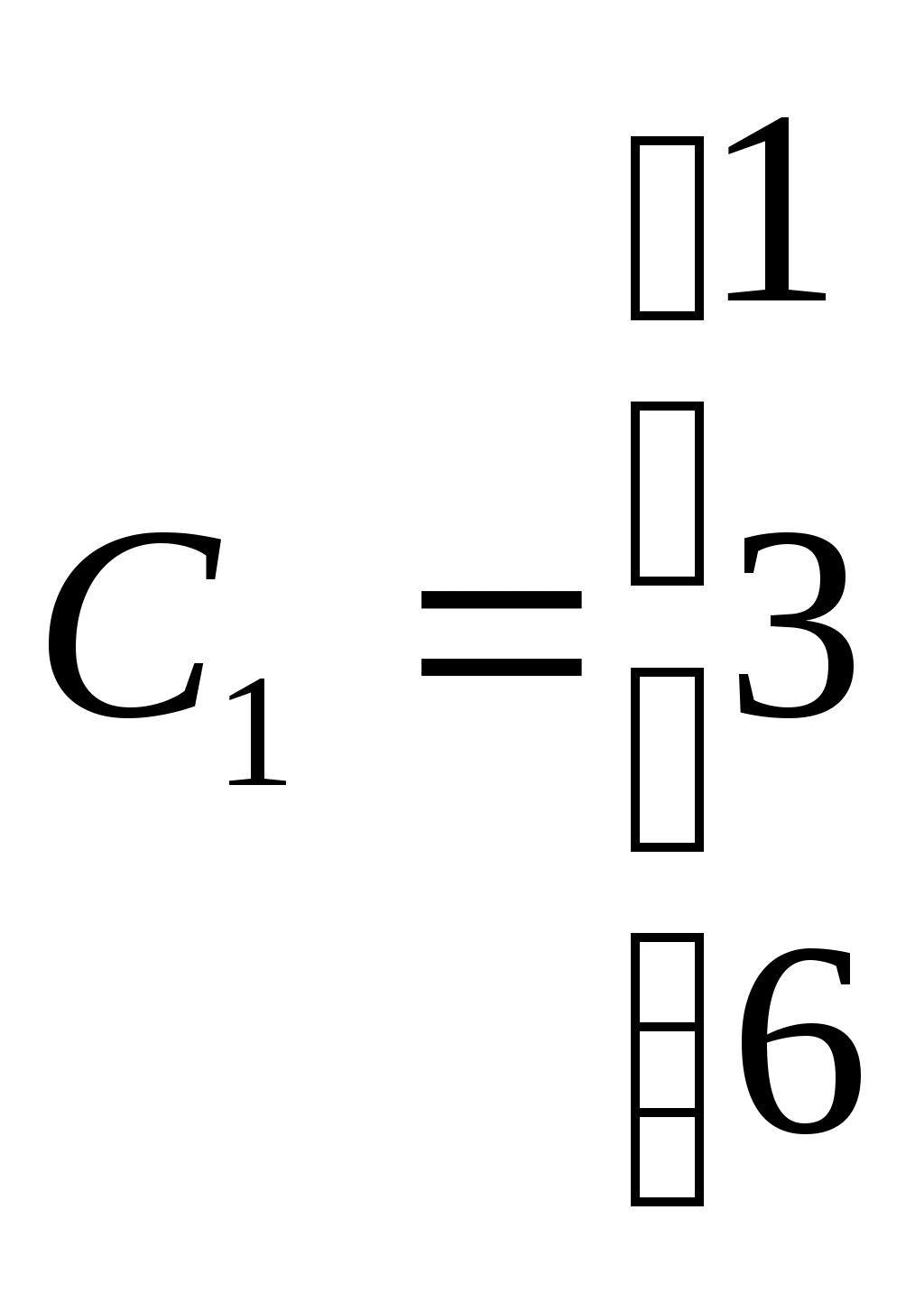
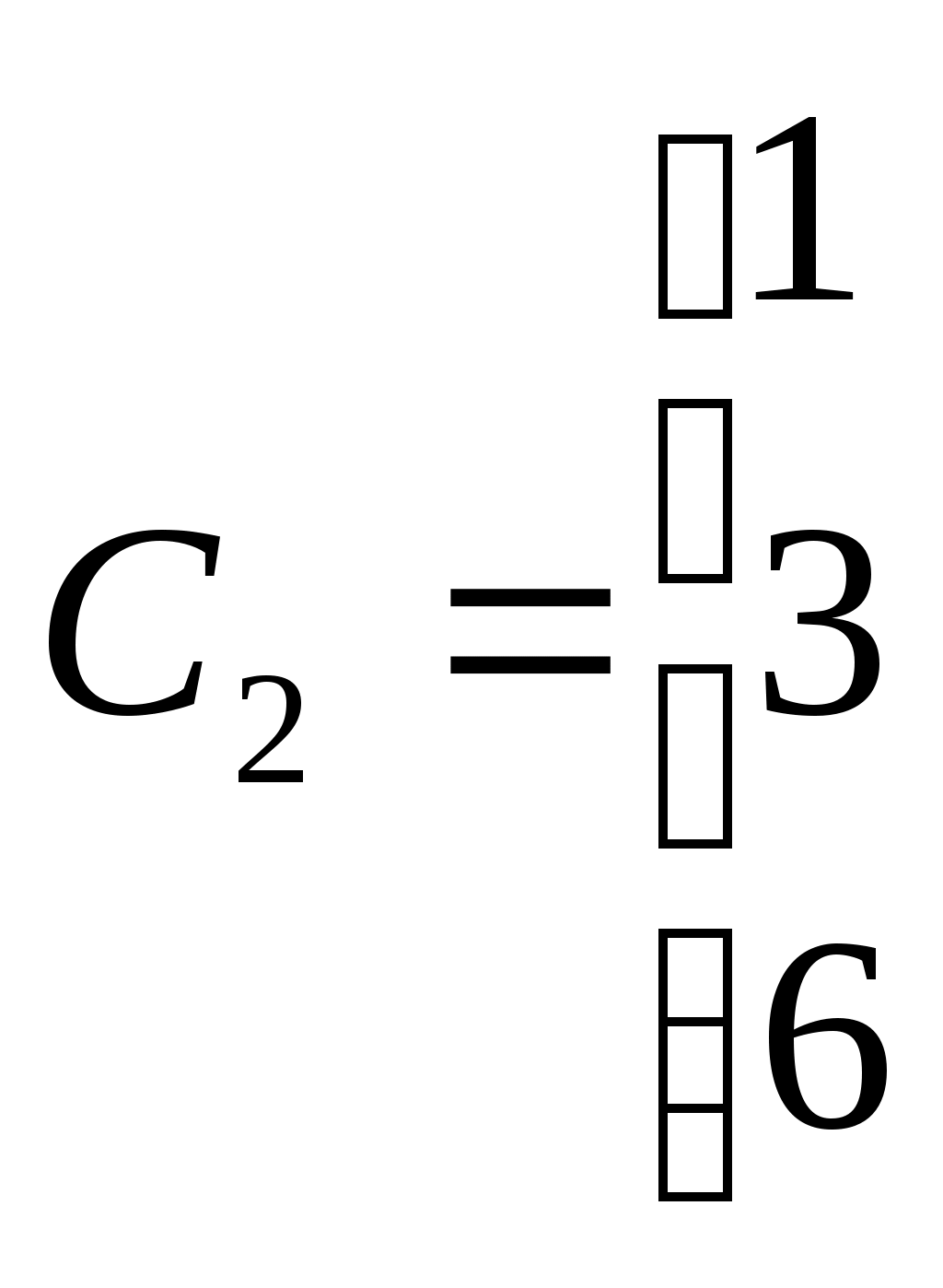
4. Зашифрованное слово запишем в виде последовательности чисел
Задача 2.3. Расшифровать текст, полученный в задаче 2.2.
Решение.
1.Вычисляется определитель
2.Определяется присоединённая матрица
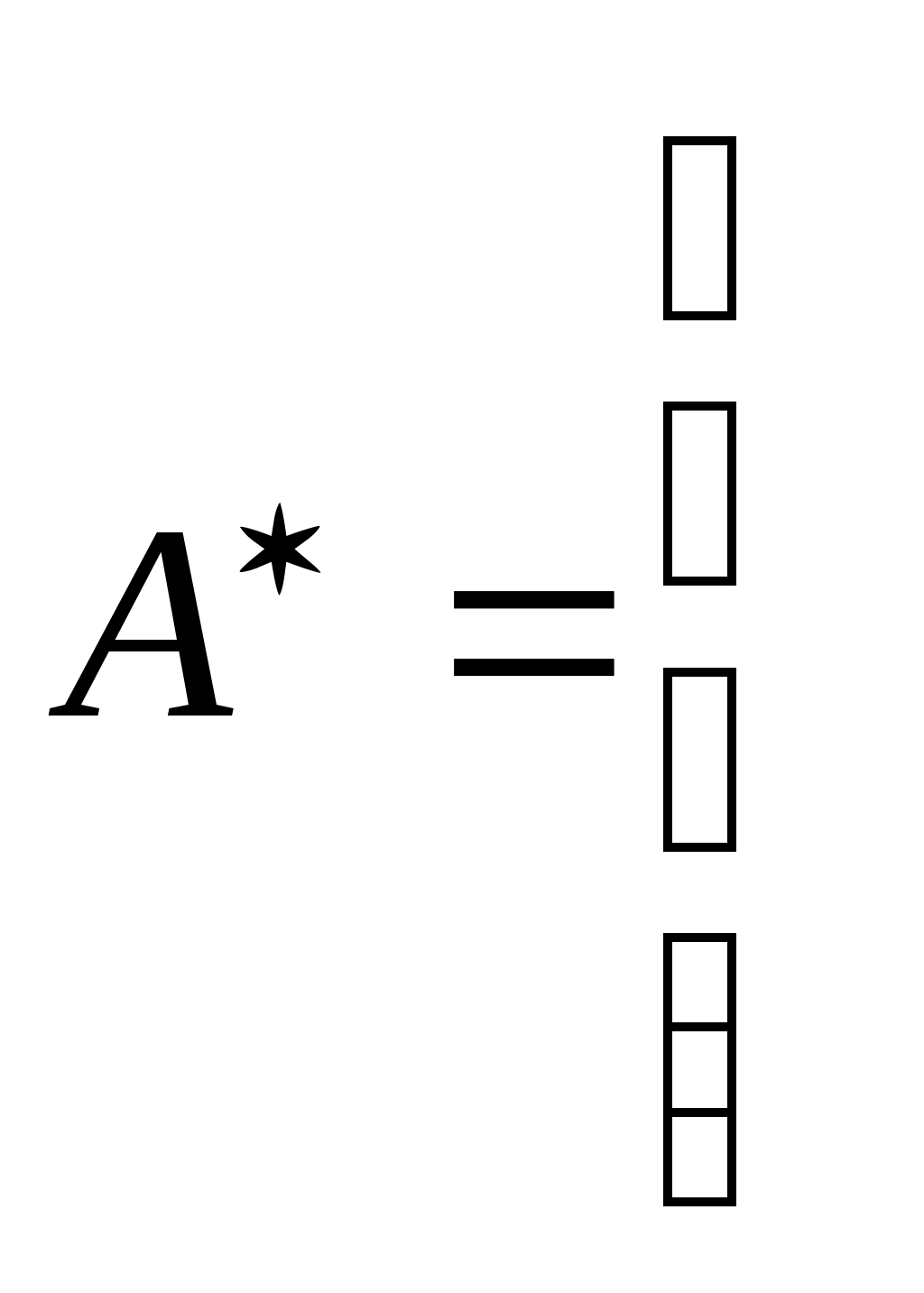
3.Получается транспонированная матрица
4.Вычисляется обратная матрица
В результате вычислений обратная матрица имеет вид:
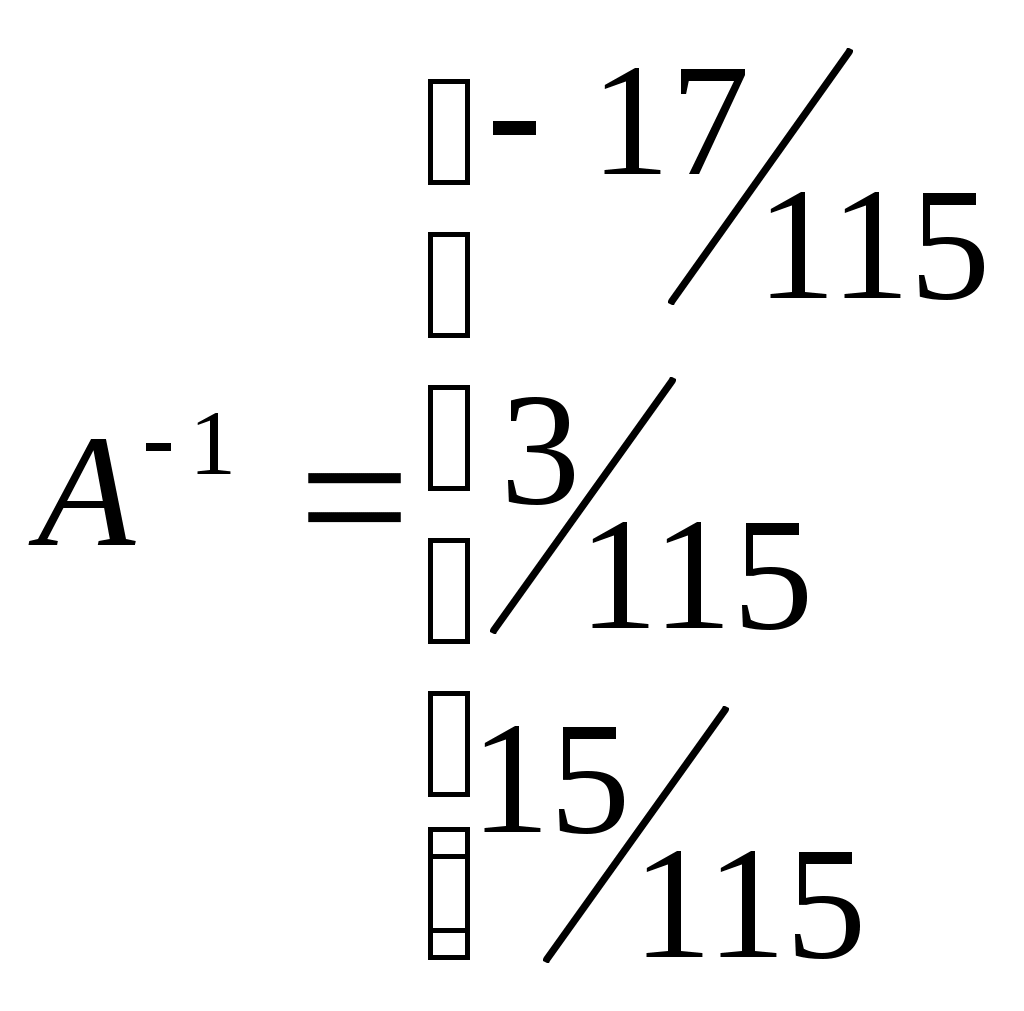
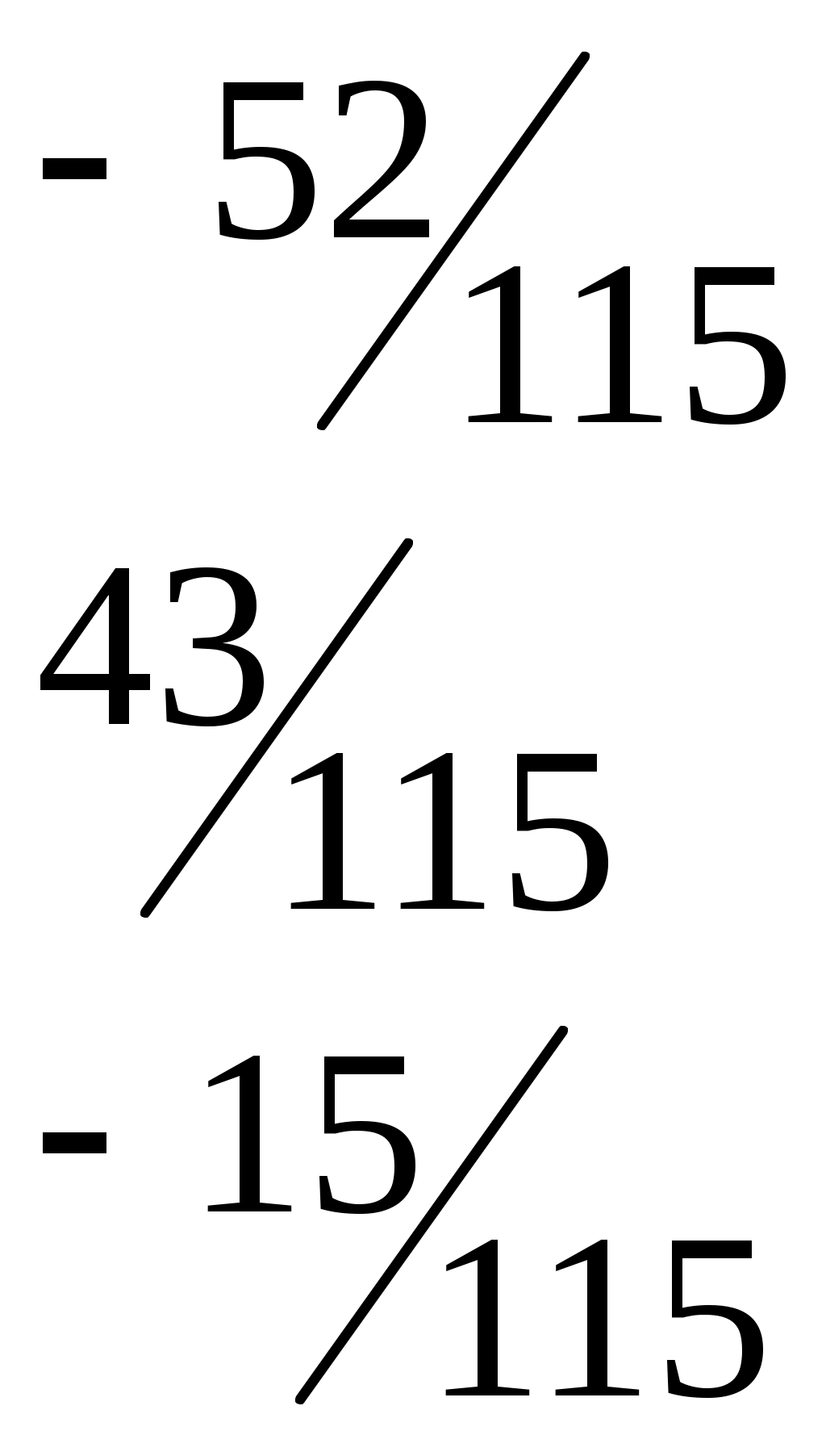
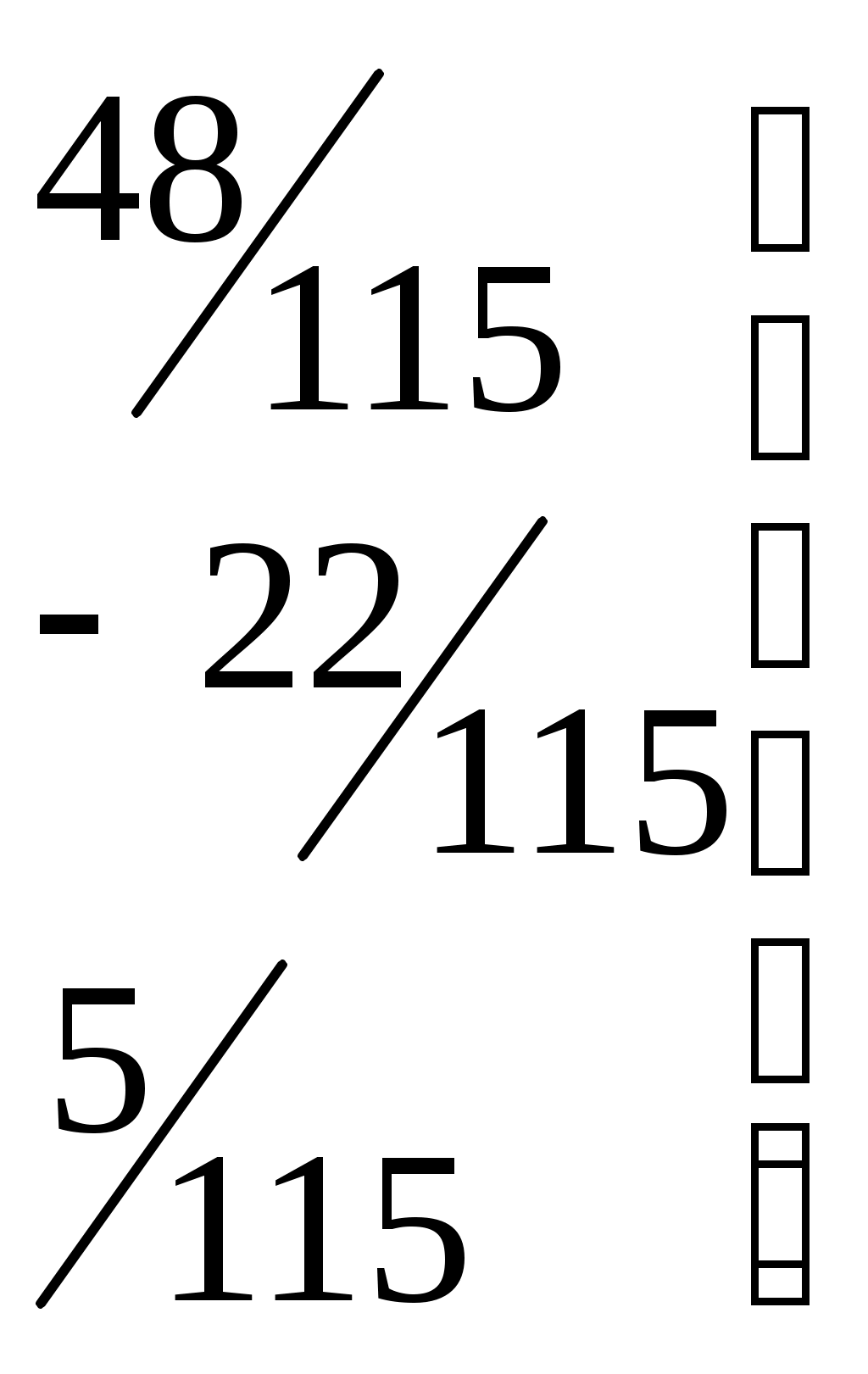
5.Определяются векторы
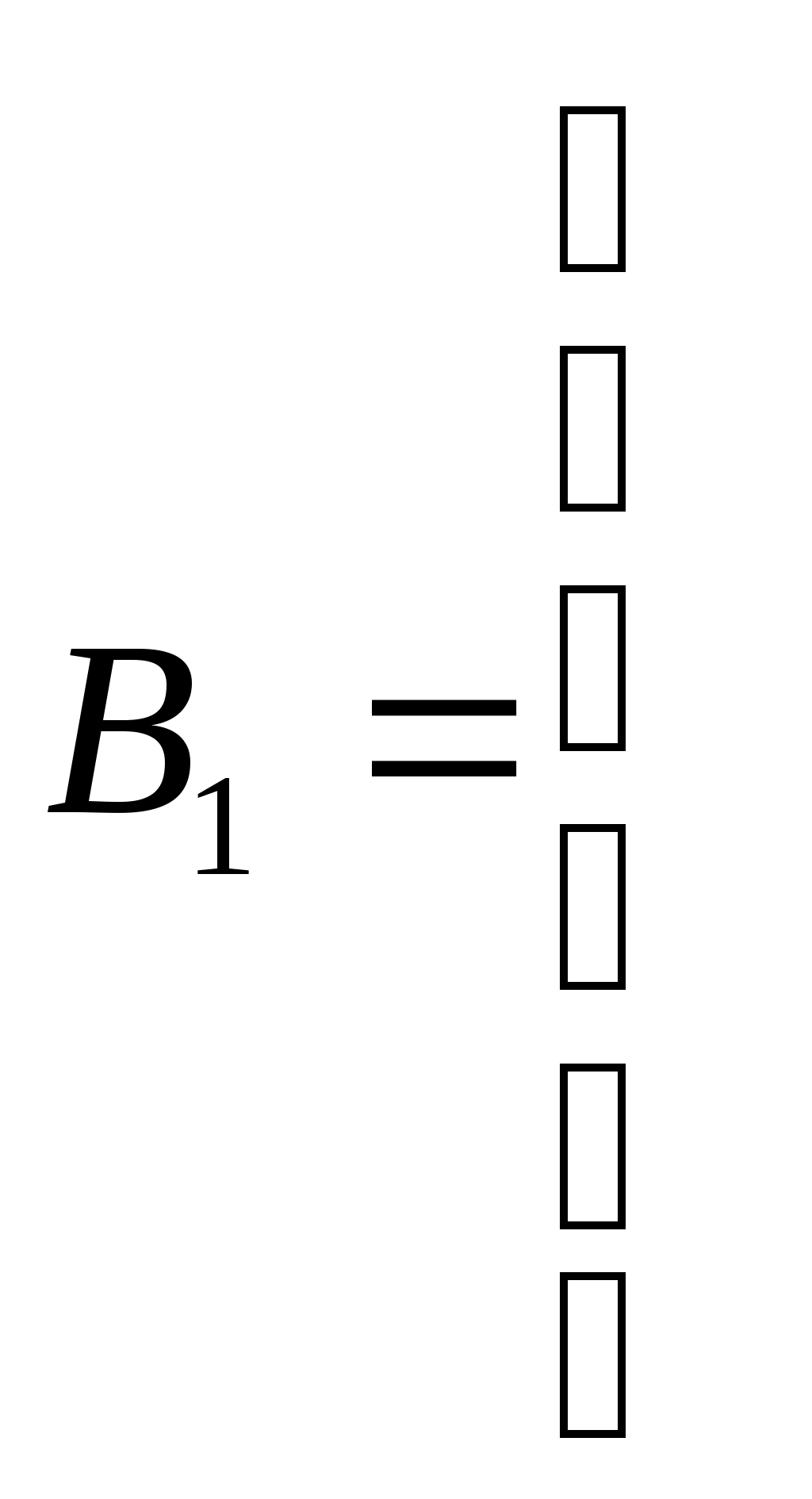
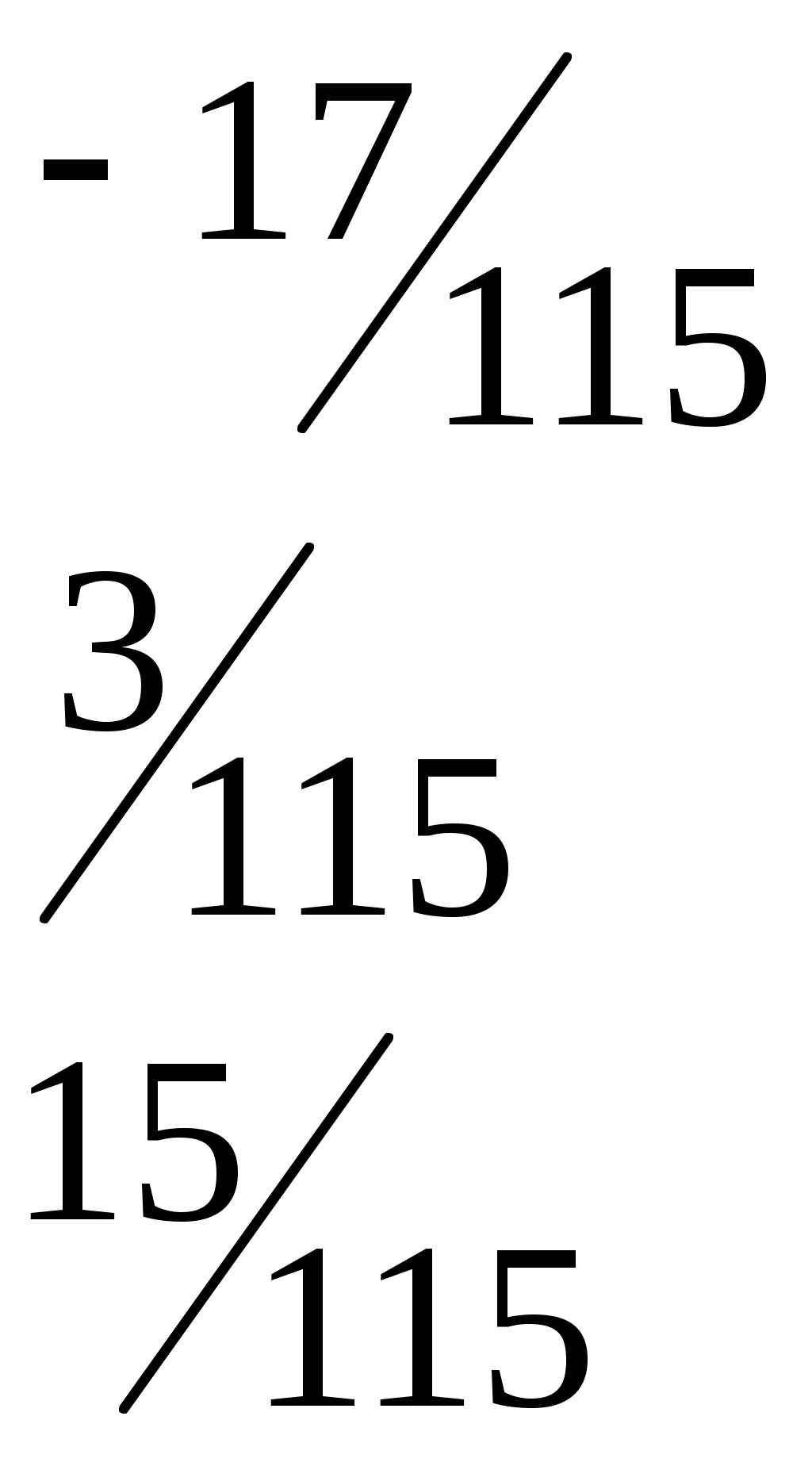
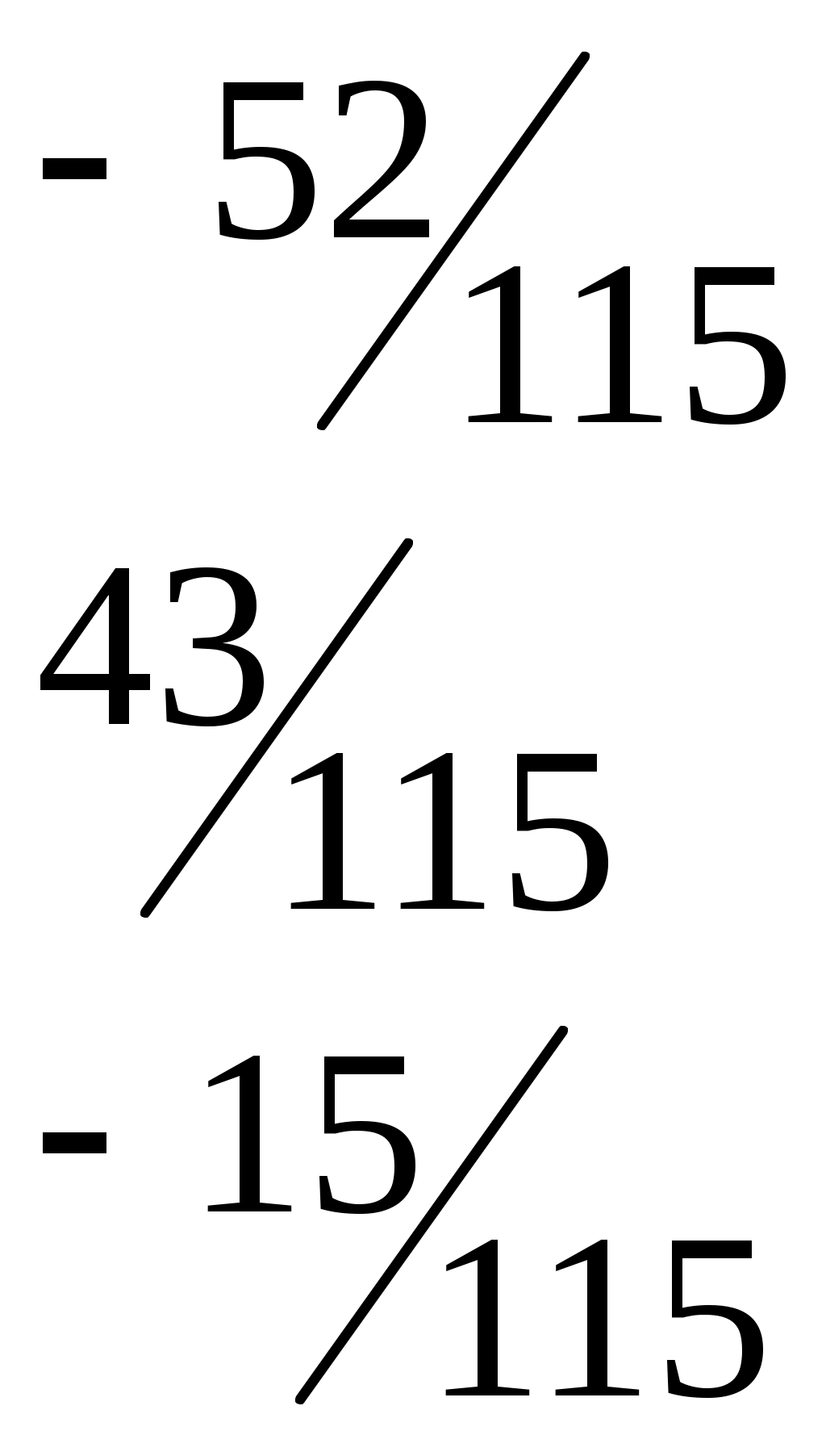
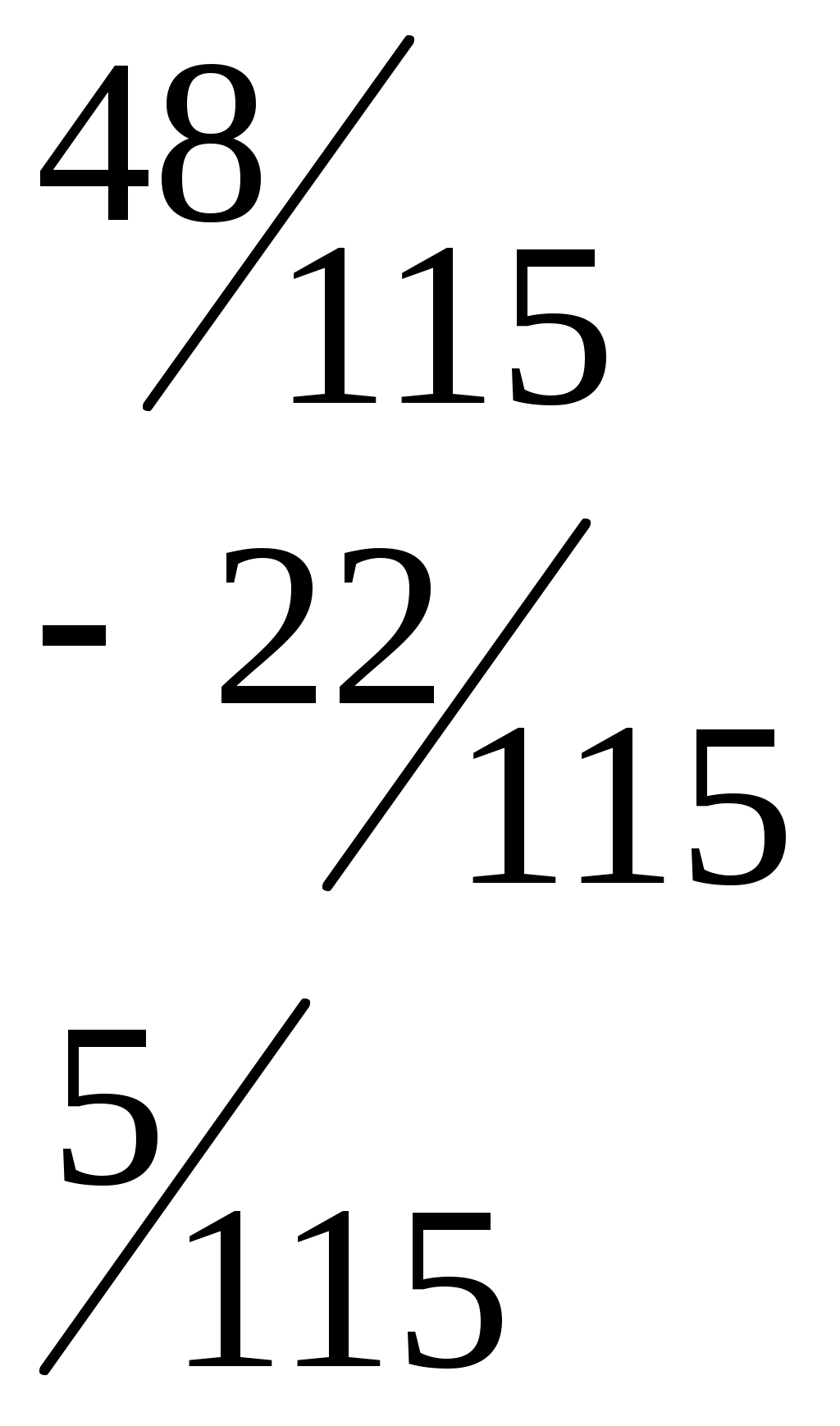
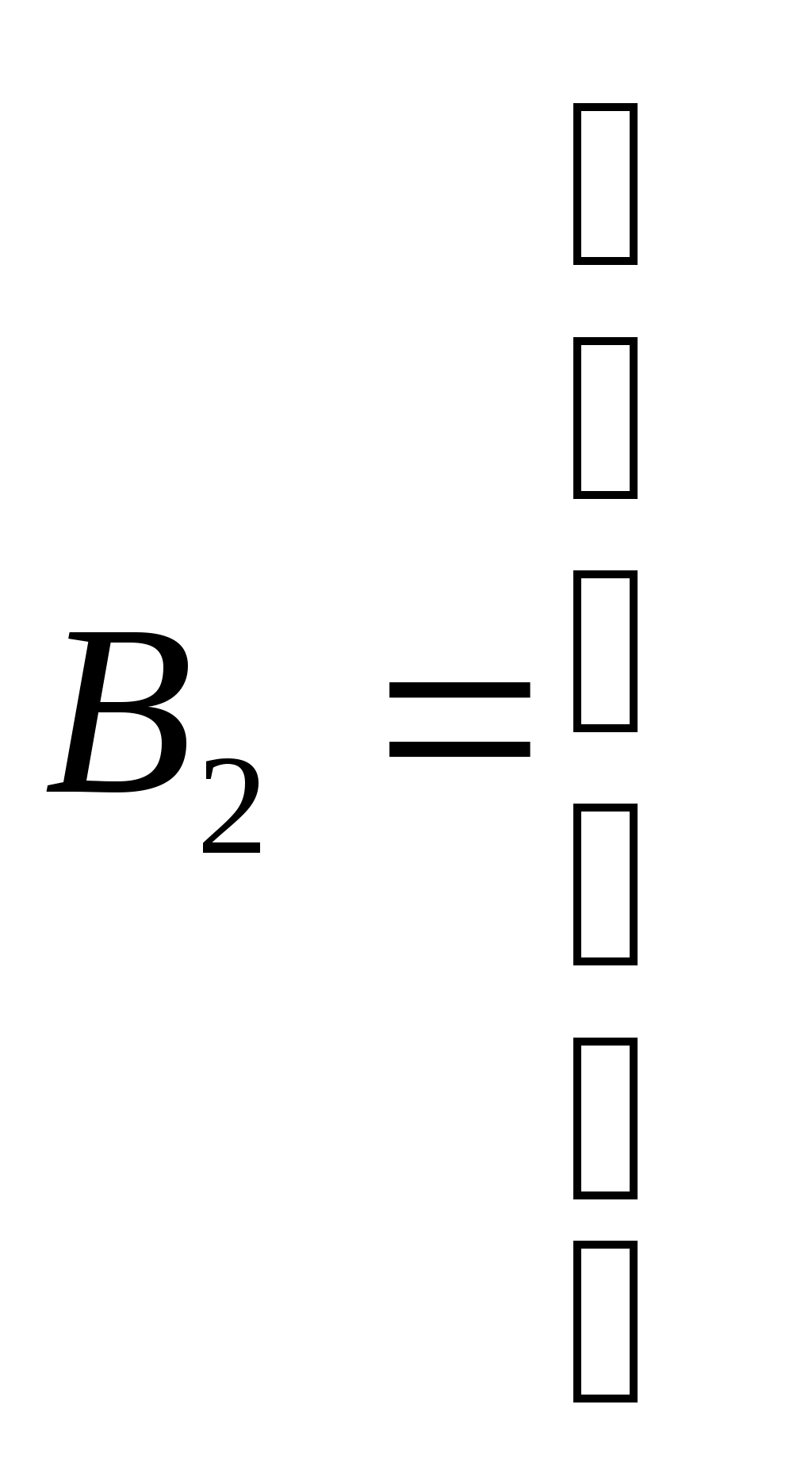
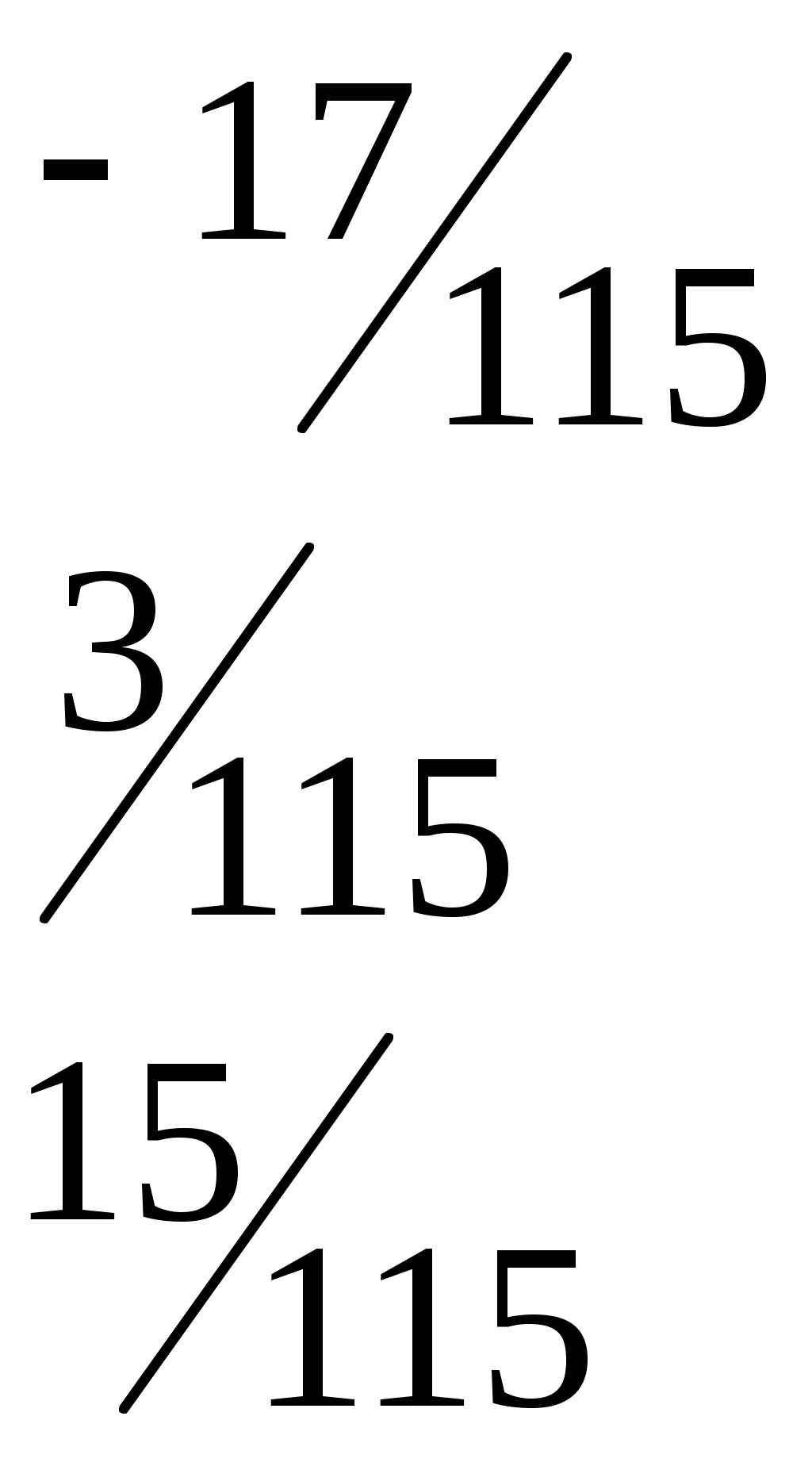
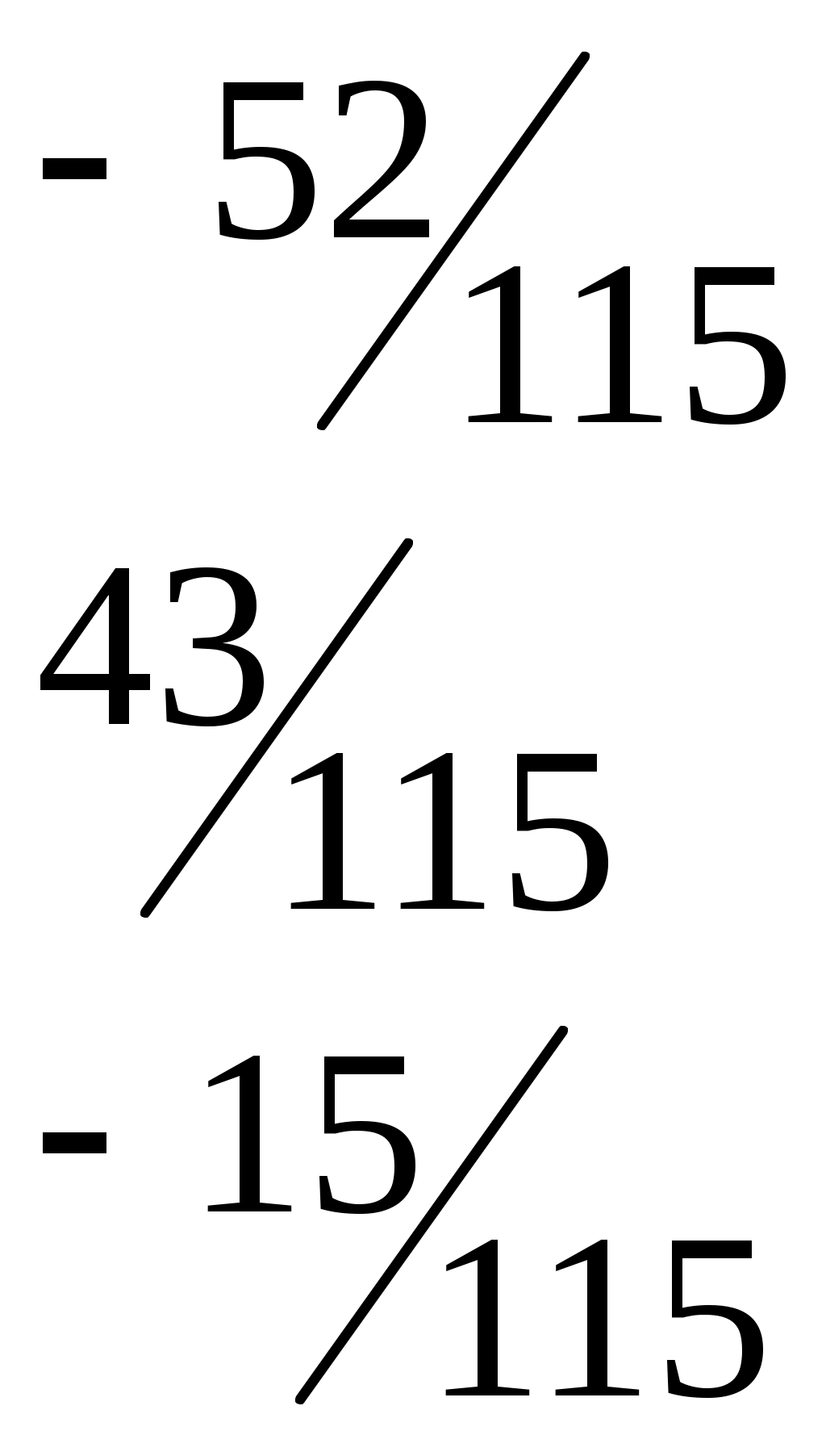
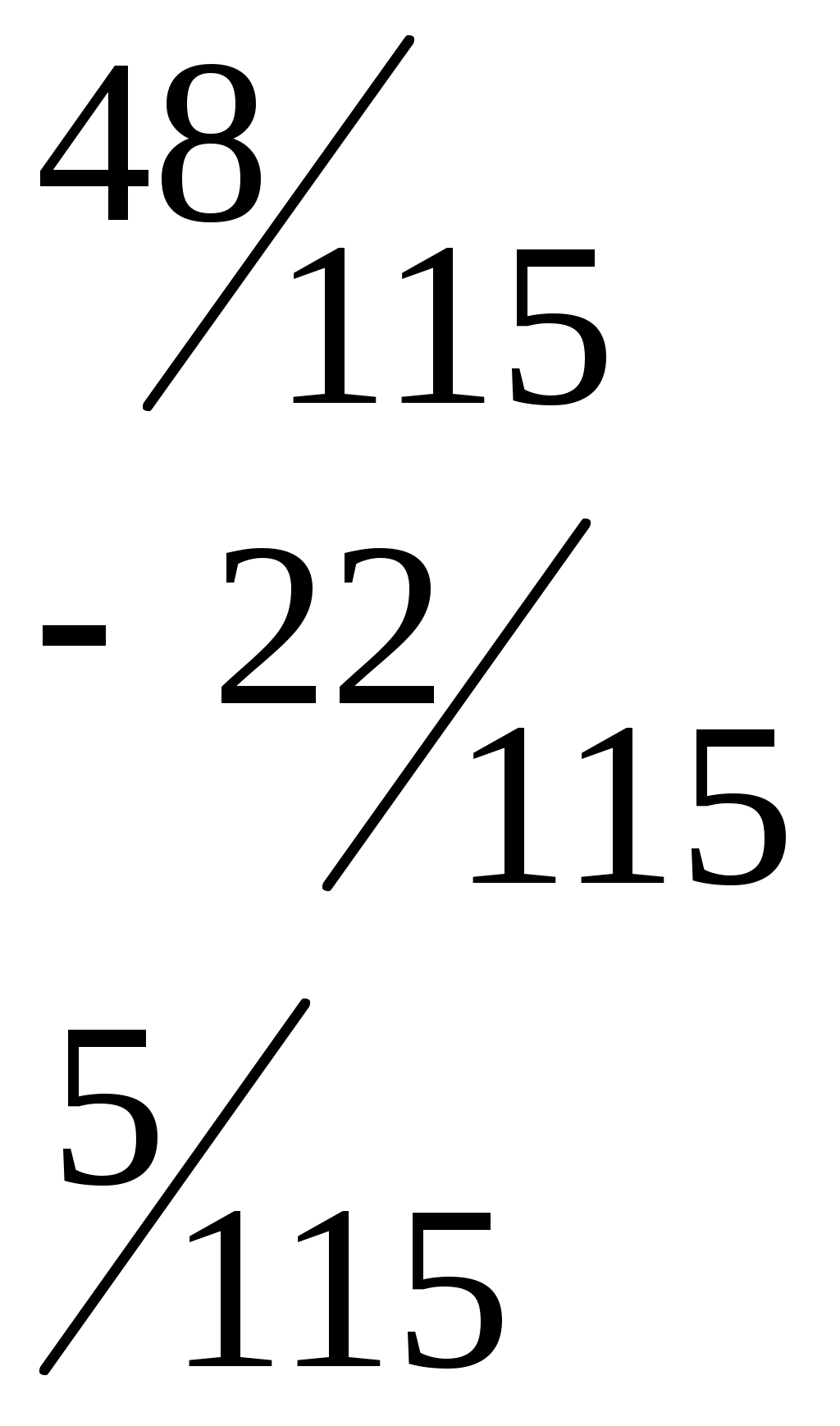
6.Получаем числовой эквивалент расшифрованного слова:
Пояснение к заданию 3
Асимметричная криптосистема RSA.
Расширенный алгоритм Евклида
-
Выбирают два больших простых числа pиq. Для большей криптостойкости pиqвыбирают равной длины. -
Вычисляют произведение: n=pq -
Вычисляют z=(p-1)(q-1) и выбирают число е взаимно простое с z, т.е. НОД (е,z)=1. -
Для вычисления закрытого (секретного) ключа d решается сравнение
еd
Решение (1) имеет вид
Для вычисления ключа dвоспользуемся расширенным алгоритмом Евклида. Для этого число
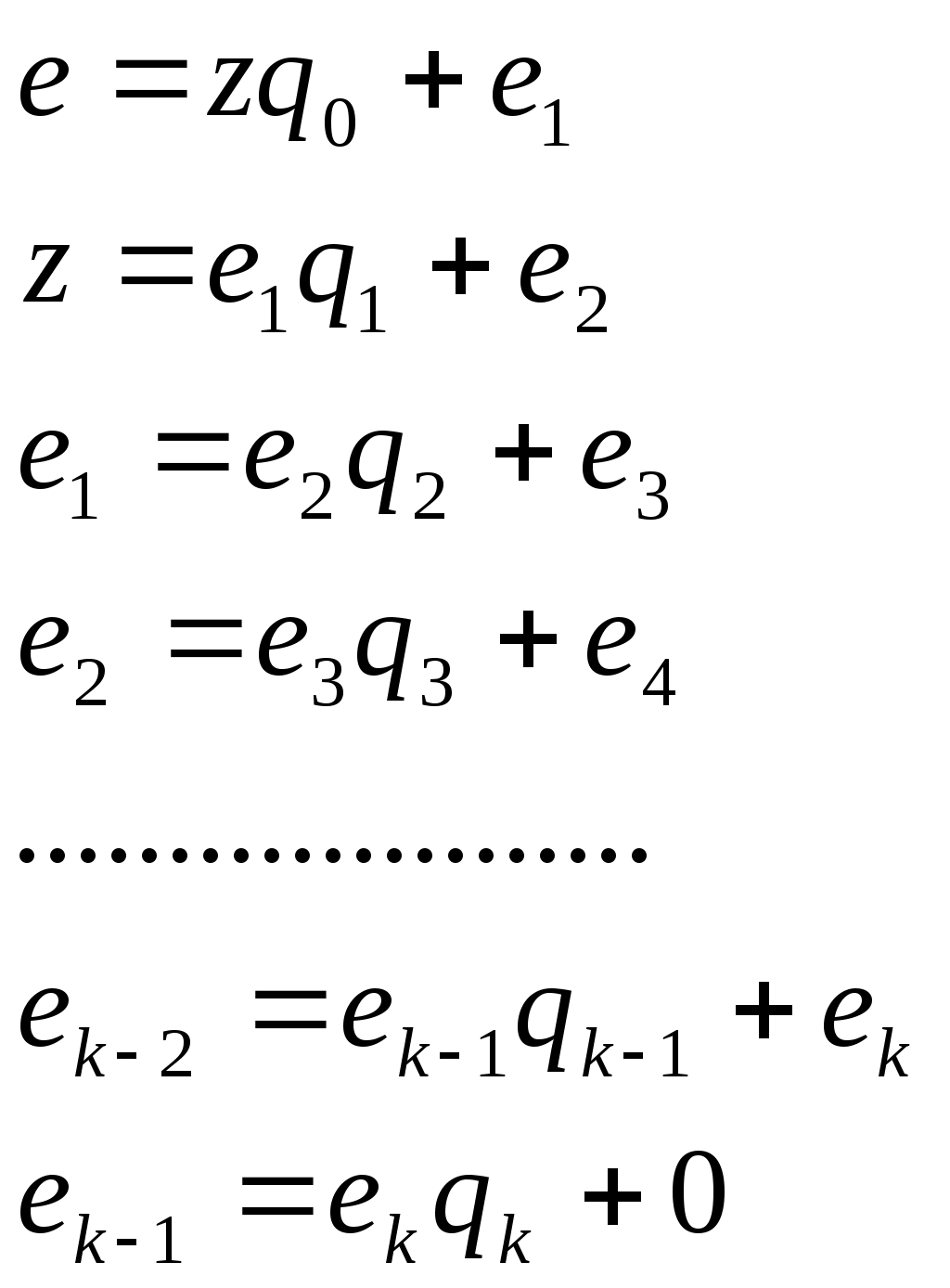
Цепная дробь имеет вид:
Их вычисления удобно оформить в виде таблицы:
| n | -2 | -1 | 0 | 1 | 2 | ……………. | k-1 | k |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
Задача 3.1.
Пусть выбраны простые числа р =47 и q=71 и открытый ключ е=79.
Требуется выполнить шифрование и дешифрование в асимметричной криптосистеме RSA сообщения:
688 232 687 966 668 3
Укажите последовательность операций.
Решение.
1.
2. Найдём секретный ключ
Воспользуемся расширенным алгоритмом Евклида:
79=3220*0+79,
3220=79*40+60,
79=60*1+19,
60=19*3+3,
19=3*6+1,
3=1*3+0.
Результаты вычислений сведём в таблицу:
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
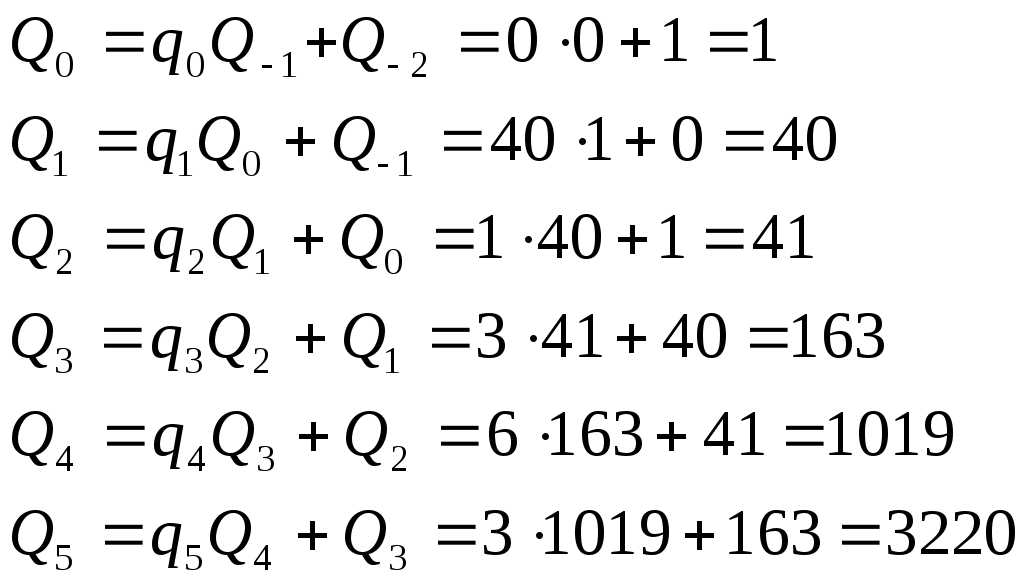
к=5
В самом деле
Следовательно, d=1019.
-
Разобьём сообщение на блоки mi, которые должны иметь длину, меньшую, чем п= pq = 47.17 =3337.
-
Затем шифруем блоки: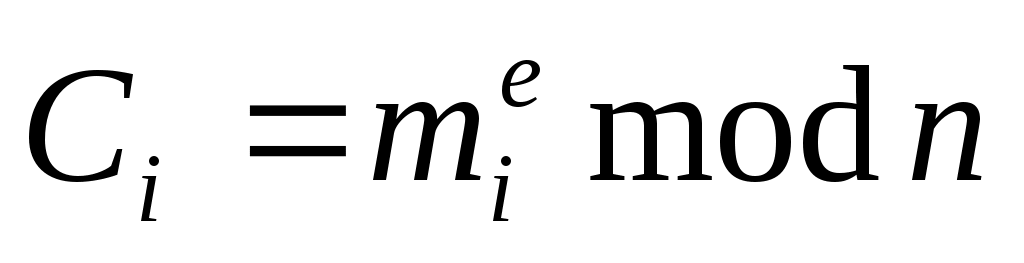
Получим криптограмму: С=(
=1570