Файл: Методические указания и контрольные задания по дисциплине информационная безопасность для студентов направления 09. 03. 02.doc

Ключ К может использоваться в качестве общего секретного ключа (ключа шифрования ключей) в симметричной криптосистеме. Кроме того, обе стороны А и В могут шифровать сообщения, используя следующее преобразование шифрования (типа RSA): С = Е_K (М) = М^К (mod N).




Для выполнения расшифрования получатель сначала нахо-

дит ключ расшифрования К* с помощью сравнения

К  К*  1 (mod N –1),

а затем восстанавливает сообщение

М = D_K (C) = C^K*(mod N).
Задача 5.1

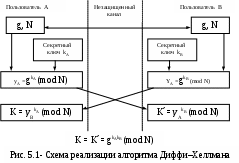
Реализовать алгоритм открытого распределения ключей Диффи-Хеллмана при следующих начальных условиях: модуль N=47, примитивный элемент g=23, секретные ключи пользователей А и В: K_А=12, К_В=33 соответственно.
Решение. Для того, чтобы иметь общий секретный ключ К, пользователи А и В сначала вычисляют значения частных открытых ключей:

y_A = (mod N)= 23¹²(mod 47) = 27 ,

y_В = (mod N)= 23³³(mod 47) = 33

После того, как пользователи А и В обменяются своими значениями y_A и y_В , они вычисляют общий секретный ключ

К = (mod N)= (mod N)= 33¹²(mod 47)= 27³³ (mod 47)= =23^12*33 (mod 47)= 25 .

Кроме того, они находят секретный ключ расшифрования, решая следующее сравнение:

К  К*  1 (mod N –1),

откуда К* = 35.

Если сообщение М =16, то криптограмма:

С = М^К =16²⁵(mod 47) = 21.

Получатель восстанавливает сообщение :

М = С^К* = 21³⁵(mod 47) =16.

Злоумышленник, перехватив значения N, g, y_А и y_В, тоже хотел бы определить значение ключа К. Очевидный путь для решения этой задачи состоит в вычислении такого значения k_А по N, g, y_А, что mod N = y_А (поскольку в этом случае, вычислив k_А, можно найти К= mod N). Однако нахождение k_А по N, g и y_А – задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой.

Выбор значений N и g может иметь существенное влияние на безопасность этой системы. Модуль N должен быть большим и простым числом. Число (N –1)/2 также должно быть простым числом. Число g желательно выбирать таким, чтобы оно было примитивным элементом множества Z

---

_N.

Алгоритм открытого распределения ключей ДиффиХеллмана позволяет обойтись без защищенного канала для передачи ключей. Однако, работая с этим алгоритмом, необходимо иметь гарантию того, что пользователь А получил открытый ключ именно от пользователя В, и наоборот. Эта проблема решается с помощью электронной подписи, которой подписываются сообщения об открытом ключе.

---

П Р И Л О Ж Е Н И Е

ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ

Модулярная арифметика

Модулярная арифметика часто изучается в школе как "арифметикачасов". Если отсчитать 14 часов от 3 часов после полудня, то получится 5 часов утра следующего дня:

3 +14 º 5 (mod 12)

или

(3 +14) mod 12 = 5.

Это арифметика по модулю 12.

Обычная запись в модулярной арифметике

a º b (mod n)

читается так: "a сравнимо с b по модулю n". Это соотношение справедливо дляцелых значений a,b и n ¹ 0, если, и только если

a = b + k * n

для некоторого целого k.

Отсюда, в частности, следует

n | (a – b).

Это читается как "n делит (a – b )".

Если a º b (mod n),

то b называют вычетом числа a по модулю n.

Операцию нахождения вычета числа a по модулю n

a (mod n)

называют приведением числа a по модулю n или приведением по модулю.

В нашем примере

(3 +14) mod 12 =17 mod 12 = 5

или

17 º 5 (mod 12),

число 5 является вычетом числа 17 по модулю 12.

Набор целых чисел от 0 до (n –1) называют полным набором вычетов по модулю n. Это означает, что для любого целого a (a > 0) его вычет r по модулю n есть некоторое целое число в интервале от 0 до (n –1), определяемое из соотношения

r = a – k * n,

где k – целое число.

Например, для n =12 полный набор вычетов:

{0, 1, 2, …, 11}.

Обычно предпочитают использовать вычеты

r Î {0, 1, 2, …, n –1},

но иногда полезны вычеты в диапазоне целых:

.

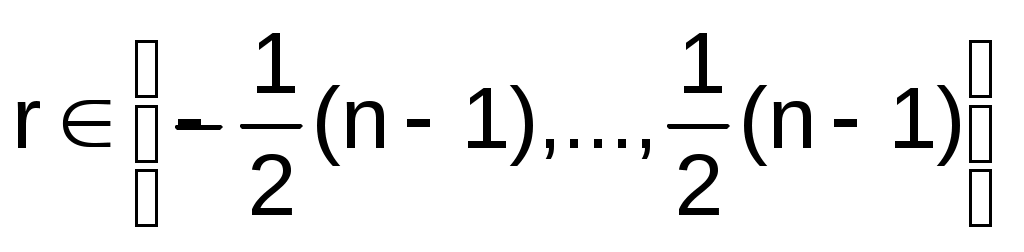Заметим, что

–12 (mod 7) º –5 (mod 7) º 2 (mod 7) º 9 (mod 7) и т.д.

Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.

Фактически мы можем либо сначала приводить по модулю n, а затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n является гомоморфным отображением из кольца целых в кольцо целых по модулю n:

(a + b) mod n = [a (mod n) + b (mod n)] mod n,

(a – b) mod n = [a (mod n) – b (mod n)] mod n,

---

(a * b) mod n = [a (mod n) * b (mod n)] mod n,

[a * (b + c)] mod n = {[a * b (mod n)] + [a * c (mod n)]} mod n.

Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата.

Для модуля n длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее

2k бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.

Вычисление степени числа a по модулю n

a^x mod n

можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).

Например, если нужно вычислить

a⁸ mod n,

не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:

(a * a * a * a * a * a * a * a) mod n.

Вместо этого выполняют три малых умножения и три малых приведения по модулю:

((a² mod n)² mod n)² mod n.

Тем же способом вычисляют

a¹⁶ mod n = (((a² mod n)² mod n)² mod n)² mod n.

Вычисление

a^x mod n,

где x не является степенью 2, лишь немного сложнее. Двоичная запись числа x позволяет представить число x как сумму степеней 2:

x = 25₍₁₀₎ ® 1 1 0 0 1₍₂₎, поэтому 25 = 2⁴ + 2³ + 2⁰.

Тогда

a²⁵ mod n = (a*a²⁴) mod n = (a*a⁸ *a¹⁶) mod n =

= a * ((a²)²)² * (((a²)²)²)² mod n = ((((a² * a)²)²)² * a) mod n.

При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a² mod n) * a) mod n)² mod n)² mod n)² mod n) * a) mod n.

Этот метод уменьшает трудоемкость вычислений до 1,5хk операций в среднем, где k – длина числа в битах.

Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n, целесообразно использовать алгоритмы быстрого возведения в степень.
Вычисление обратных величин

В арифметике действительных чисел нетрудно вычислить мультипликативную обратную величину a

---

^–1 для ненулевого a:

a^–1 =1/a или a * a^–1 =1.

Например, мультипликативная обратная величина от числа 4 равна 1/4, поскольку

4 * =1.

В модулярной арифметике вычисление обратной величины является более сложной задачей. Например, решение сравнения

4 * x º1 (mod 7)

эквивалентно нахождению таких значений x и k, что

4 * x º 7 * k +1,

где x и k – целые числа.

Общая формулировка этой задачи – нахождение такого целого числа x, что

a * x (mod n) =1.

Можно также записать

a^–1 º x (mod n).

Решение этой задачи иногда существует, а иногда его нет. Например, обратная величина для числа 5 по модулю 14 равна 3, поскольку

5 * 3 =15 º 1 (mod 14).

С другой стороны, число 2 не имеет обратной величины по модулю 14.

Вообще сравнение

a^–1 º x (mod n)

имеет единственное решение, если a и n – взаимно простые числа.

Если числа a и n не являются взаимно простыми, тогда сравнение

a^–1 º x (mod n)

не имеет решения.

Сформулируем основные способы нахождения обратных величин. Пусть целое число a Î {0, 1, 2, …, n – 1}.

Если НОД (a, n) =1, то a * i (mod n) при i= 0, 1, 2, …, n –1 является перестановкой множества {0, 1, 2, …, n – 1}.

Например, если a = 3 и n = 7 (НОД (3,7) =1), то

3 * i (mod 7) при i= 0, 1, 2, …, 6

является последовательностью 0, 3, 6, 2, 5, 1, 4, т.е. перестановкой множества {0, 1, 2, …, 6}.

Это становится неверным, когда НОД (a, n) ¹ 1. Например, если a = 2 и n = 6, то

2 * i (mod 6) º 0, 2, 4, 0, 2, 4 при i= 0, 1, 2, …, 5.

Если НОД (a,n) =1, тогда существует обратное число a^–1, 0 < a^–1 < n, такое, что

a * a^–1 º1 (mod n).

Действительно, a * i (mod n) является перестановкой 0, 1, ..., n –1, поэтому существует i, такое, что

a * i º1 (mod n).

Как уже отмечалось, набор целых чисел от 0 до n –1 называют полным набором вычетов по модулю n. Это означает, что для любого целого числа a (a > 0) его вычет r = a (mod n) – это некоторое целое число в интервале от 0 до n –1.

Выделим из полного набора вычетов подмножество вычетов, взаимно простых с n. Такое подмножество называют приведенным набором вычетов.

Пример. Пусть модуль n =11 – простое число. Полный набор вычетов по модулю 11

{0, 1, 2, …, 10}.

При формировании приведенного набора вычетов из них удаляется только один элемент – 0. Приведенный набор вычетов по модулю 11 имеет 11 – 1 = 10 элементов.

---