Файл: Структурный анализ механизма.docx

Скачать файл (0,63Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 80

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Коэффициенты запаса прочности по нормальным напряжениям

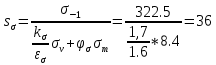
Коэффициенты запаса прочности по касательным напряжениям

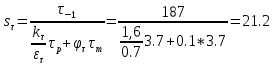
Результирующий коэффициент запаса прочности для сечения A-A

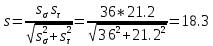
Сечение К - К

Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом

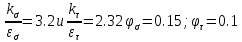
Изгибающий момент

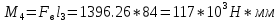
Осевой момент сопротивления

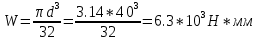
Амплитуда нормальных напряжений

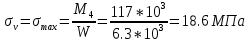
Полярный момент сопротивления

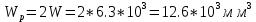
Амлитуда и среднее напряжение цикла касательных напряжений

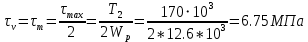
Коэффициент запаса прочности по касательным напряжениям

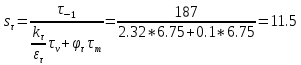
Коэффициент запаса прочности по нормальным напряжениям

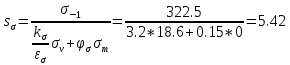
Результирующий коэффициент запаса прочности для сечения К-К

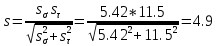
Сечение Л – Л

Концентрация напряжений обусловлена переходом от  40 мм к  38 мм: при

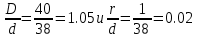
Коэффициенты концентрация напряжений k_=2.08 и k_=1.24;

Масштабные факторы _ =0.85; _ =0.73;

Внутренние силовые факторы те же, что и для сечениия Л-Л.

Осевой момент сопротивления сечения

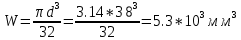
Амплитуда нормальных напряжений

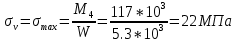
Полярный момент сопротивления

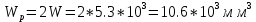
Амплитуда и среднее напряжение цикла касательных напряжений

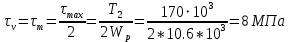
Коэффициент запаса прочности по касательным напряжениям

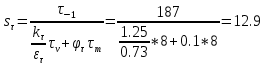
Коэффициент запаса прочности по нормальным напряжениям

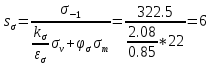
Результирующий коэффициент запаса прочности для сечения Л-Л

Сечение Б – Б

Концентрация напряжений обусловлена наличием шпоночной канавки:

k =1,75 и k = 1,6;  = 0,85;  = 0,73.

Изгибающий момент (положим х1 = 60 мм)

Внутренние силовые факторы те же, что и для сечения Б-Б

Осевой момент сопротивления качения

Амплитуда нормальных напряжений

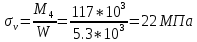
Полярный момент сопротивления

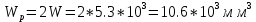
Амплитуда и среднее напряжение цикла касательных напряжений

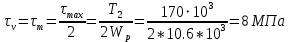
Коэффициент запаса прочности по нормальным напряжениям

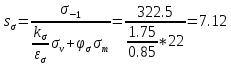
Коэффициент запаса прочности по касательным напряжениям

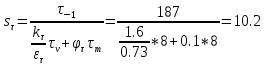
Результирующий коэффициент запаса прочности для сечения Б-Б

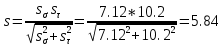
Сведем результаты проверки в таблицу:

Сечение	А-А	К-К	Л-Л	Б-Б
Коэф. s	18.3	4.9	5.44	5.84

Расчетное значение s должно быть не ниже допускаемого [s] = 2,5.

Во всех сечениях s > [s]
2 Расчёт валов на усталостную прочность

11.Уточненный расчет валов

Уточненный расчет состоит в определении коэффициентов запаса прочности s для опасных сечений и сравнении их с допускаемыми значениями [s]. Прочность соблюдена при s  [s]. Будем производить расчет для предположительно опасных сечений каждого из валов.

Среднее значение _в = 780 МПа. Предел выносливости при симметричном цикле изгиба

При симметричном цикле изгиба:

σ_-1 ≈ 0,43 * σ_в = 0,43 * 750 = 322.5 МПа;

При симметричном цикле касательных напряжений:

τ_-1 ≈ 0,58 * σ_-1 = 0,58 * 322,5 = 187 МПа;

Расчет сечений тихоходного вала на сопротивление усталости

Материал- углеродистая сталь 45

Механические характеристики выбранного материала:

Н/мм²;

Н/мм²;

Коэффициент

В расчетах валов принимают, что нормальные напряжения изменяются по симметричному циклу

, а касательные напряжения – по от нулевого циклу

.

Амплитуду напряжений цикла в опасном сечении вычисляют по формулам:

;

;

где

;

- моменты сопротивления сечения вала при изгибе и кручении;

- результирующий изгибающий момент;

- крутящий момент.

Сечение А.

Это сечение при передаче вращающего момента от электродвигателя через муфту рассчитываем на кручение. Концентрацию напряжений вызывает наличие шпоночной канавки.

Коэффициент запаса прочности

Где амплитуда и среднее напряжение:

При d=18мм; b=6; t₁=3,5

Принимаем k_τ=1.6 ; ψ_τ ≈0.1

Коэффициент запаса прочности

ГОСТ 16162-78 указывает на то, чтобы конструкция редукторов предусматривала возможность восприятия радиальной консольной нагрузки, приложенной в середине посадочной части вала. Величина этой нагрузки для одноступенчатых зубчатых редукторов на быстроходном валу должна быть

Приняв у ведущего вала длину посадочной части под муфту равной длине полумуфты l = 50 мм (муфта УВП для валов диаметром 20 мм), получим изгибающий момент в сечении А – А от консольной нагрузки

Коэффициент запаса прочности по нормальным напряжениям

Результирующий коэффициент запаса прочности

получился близким к коэффициенту запаса

= 6,83. Это незначительное расхождение свидетельствует о том, что консольные участки валов, рассчитанные по крутящему моменту и согласованные с расточками стандартных полумуфт, оказываются прочными и что учет консольной нагрузки не вносит существенных изменений. Фактическое расхождение будет еще меньше, так как посадочная часть вала обычно бывает короче, чем длина полумуфты, что уменьшает значения изгибающего момента и нормальных напряжений. Такой большой коэффициент запаса прочности (6.3 или 6.831) объясняется тем, что диаметр вала был увеличен при конструировании для соединения его стандартной муфтой с валом электродвигателя. По той же причине проверять прочность в сечениях Б — Б и В — В нет необходимости.

Сечение А — А

Диаметр вала в этом сечении 50 мм. Концентрация напряжений обусловлена наличием шпоночной канавки: k_ =1,75 и k_ = 1,6; масштабные факторы _ = 0,82; _ = 0,70; коэффициенты _  0, 15 и _  0,1.

Крутящий момент Т₂=