Файл: Оглавление Введение Основные понятия и определения тмм.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 152
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;  , причём выполнение условия
, причём выполнение условия  решается при
решается при
рис. 97 моментном (динамическом) уравновешивании, которое называется уравновешиванием второго рода.
10.2. Уравновешивание с помощью противовесов на звеньях механизма
Рассмотрим последовательность статического уравновешивания на примере четырёхшарнирного механизма (рис. 98, а). Заменяем массы звеньев 1, 2, 3 сосредоточенными массами в точках A, B, C, D, причём в силу неподвижности точек A и D, массы, сосредоточенные в этих точках, можно не учитывать.
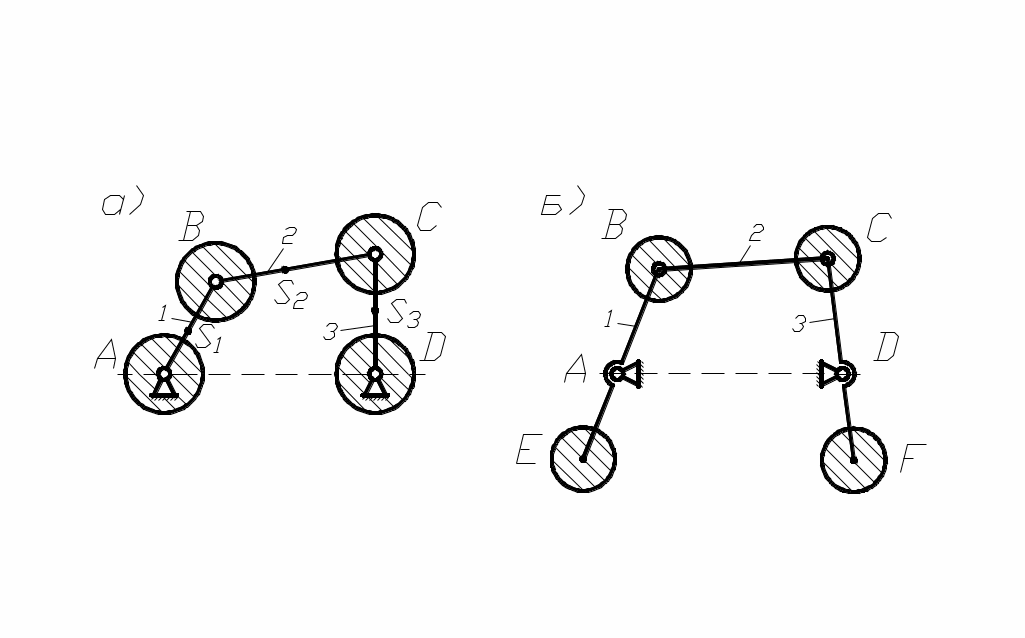
рис. 98
Приведённые массы в точках В и С равны:
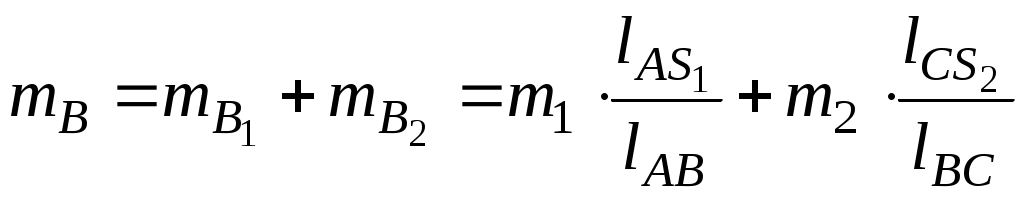 ;
;
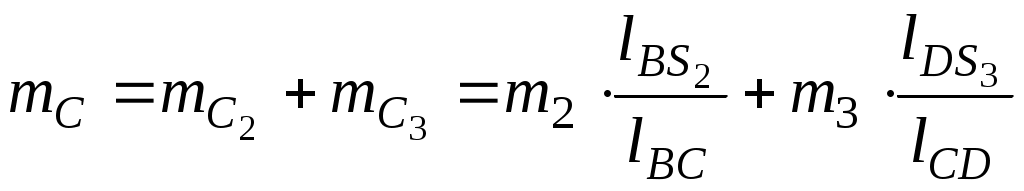 .
.
Так как заменяющие массы mB и mC совершают вращательное движение, то для уравновешивания сил инерции необходимы противовесы с массами mЕ и mF, определяемыми из условий (рис. 98, б):
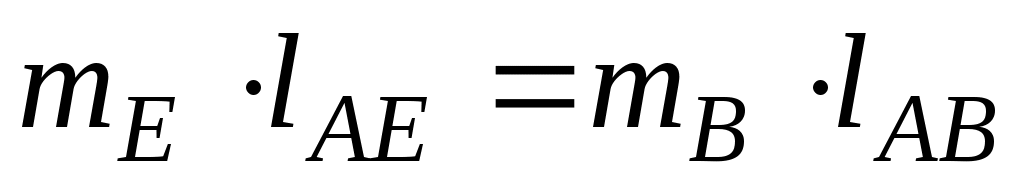 ;
; 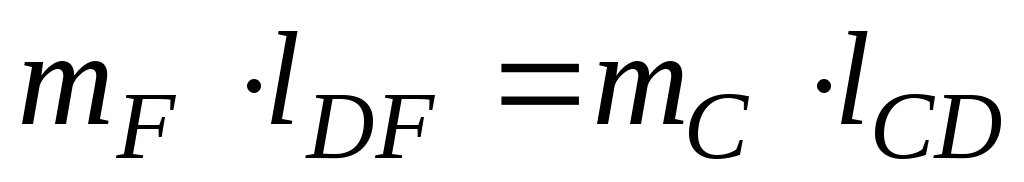 ,
,
где, задавая длины противовесов, можно получить их массы и наоборот.
Рассмотрим моментное уравновешивание на примере четырёхшарнирного механизма. Его приближённое моментное уравновешивание можно осуществить после статического уравновешивания, введя в схему механизма два одинаковых дополнительных противовеса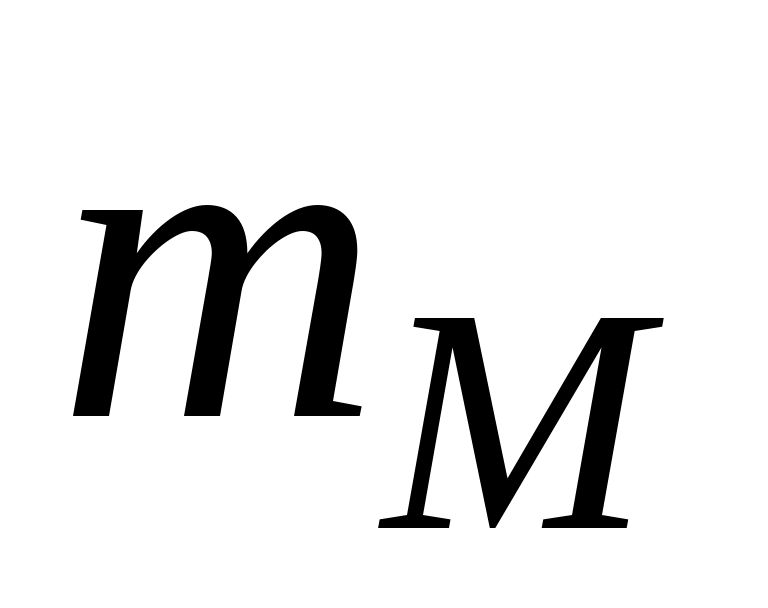 (рис. 99),
(рис. 99), 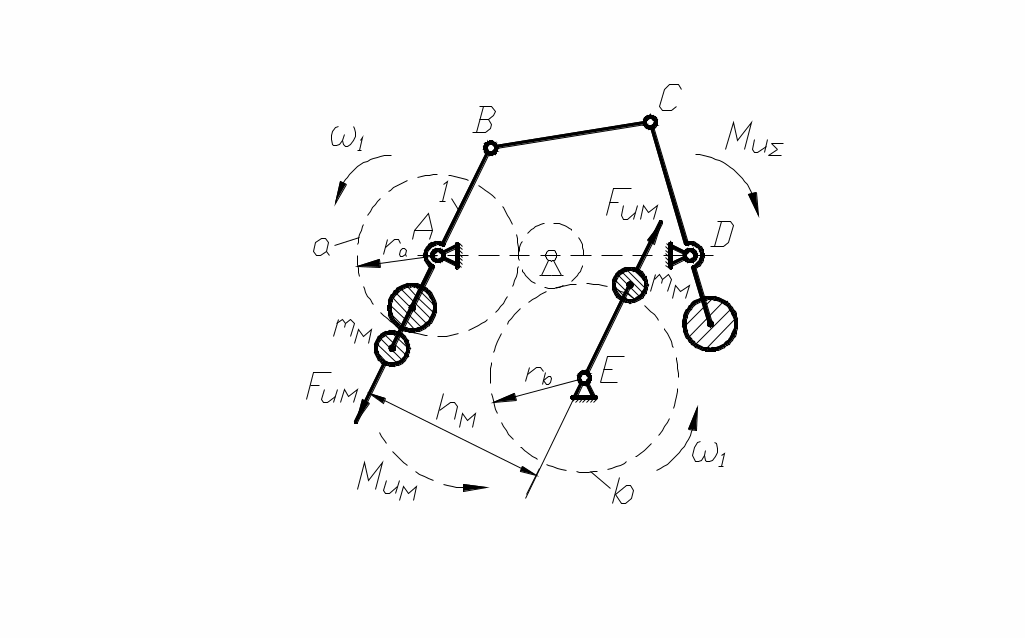 соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой скоростью
соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой скоростью 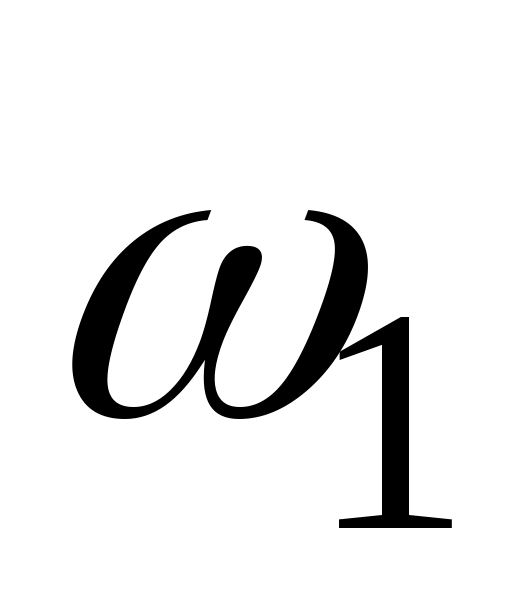 , а равное ему колесо “b”
, а равное ему колесо “b”
рис. 99 вращается с той же угловой скоростью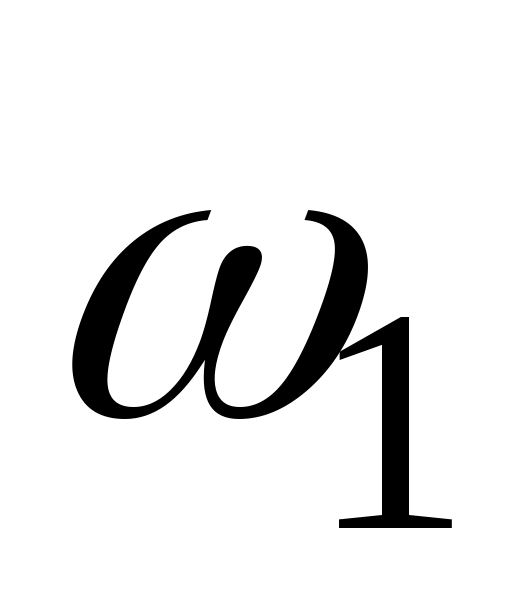 , но угловые координаты противовесов отличаются на 1800, поэтому момент пары сил инерции от противовесов
, но угловые координаты противовесов отличаются на 1800, поэтому момент пары сил инерции от противовесов 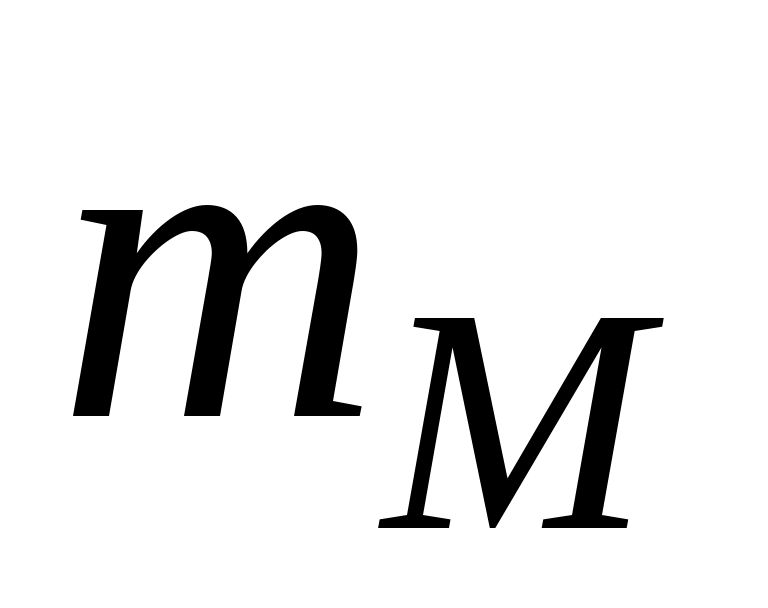
равен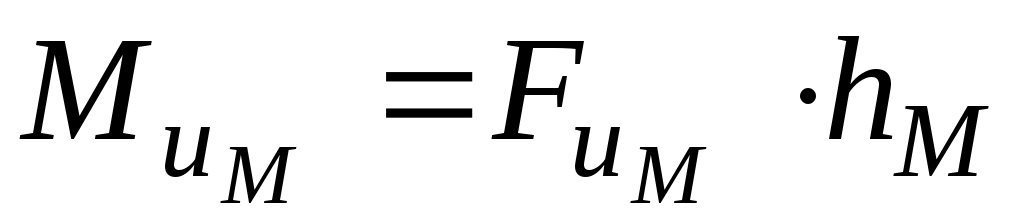 . Подбирая положение точки E, можно обеспечить направление
. Подбирая положение точки E, можно обеспечить направление 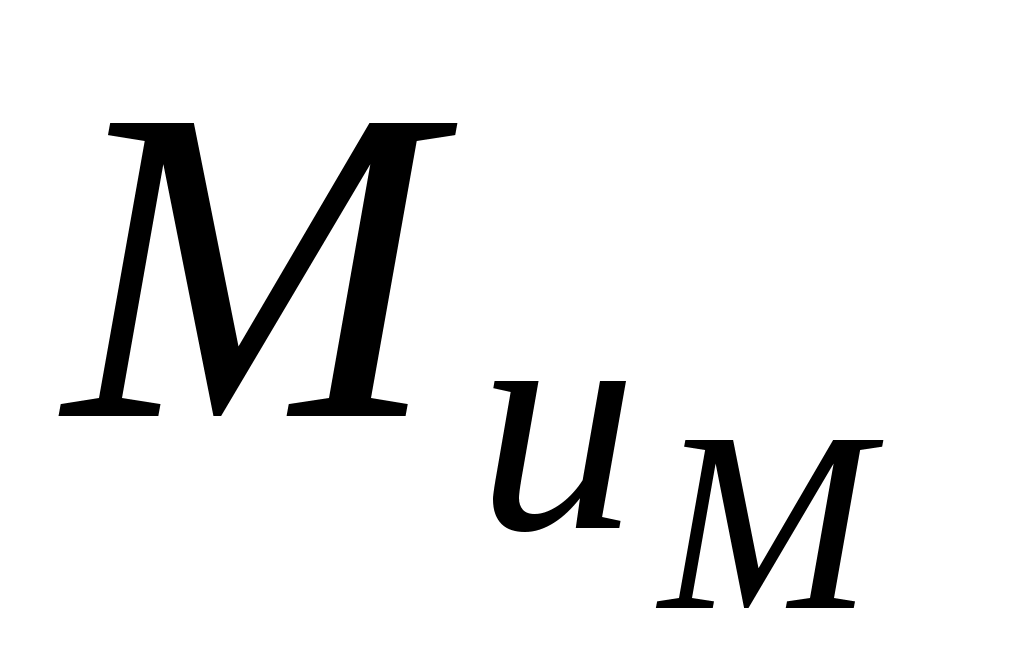 , противоположное направлению
, противоположное направлению 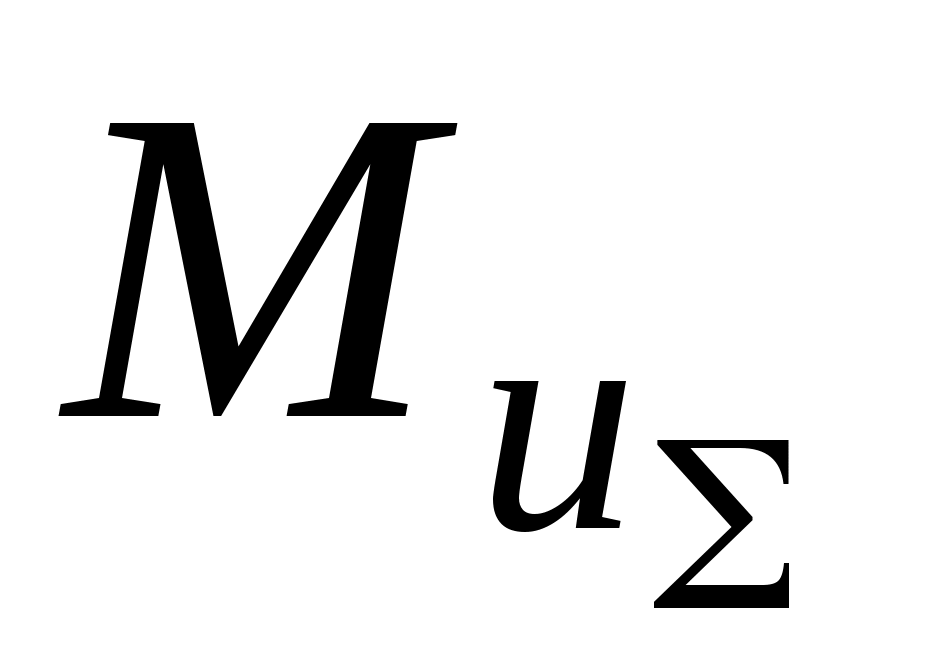 , а массу противовесов
, а массу противовесов  определяют из условия
определяют из условия 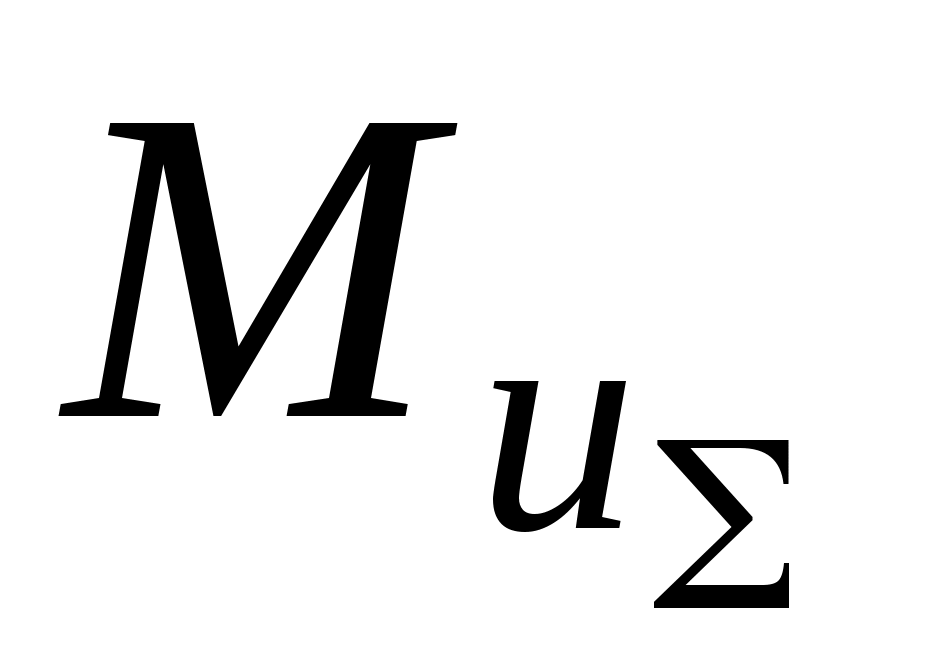 =
= 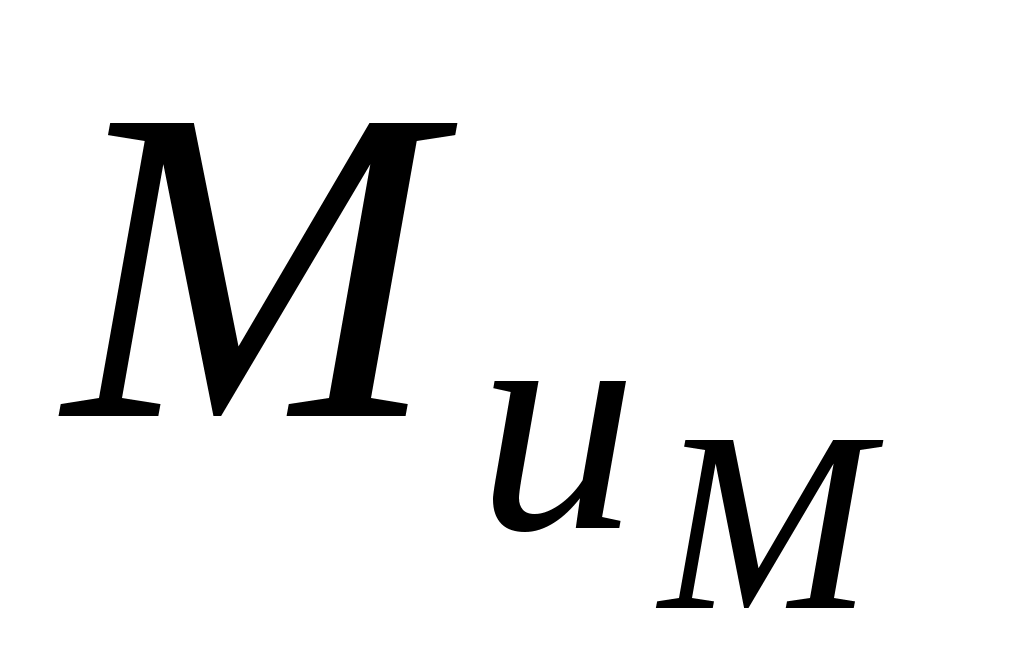 .
.
10.3. Уравновешивание вращающихся масс (роторов)
Ротором в теории балансировки называется любое вращающееся тело. В связи с появлением быстроходных машин возникла проблема уравновешивания быстровращающихся деталей. Так, например, скорость некоторых турбин, валов гироскопов, суперцентрифуг достигает 3÷50 тысяч об/мин и малейшее смещение центра масс с геометрической оси вращения вызывает появление больших сил инерции, т.е. вибрационных явлений в машине и фундаменте.
Различают статическое уравновешивание (статическая балансировка) вращающихся роторов и динамическое. Статическая балансировка достигается тем, что центр тяжести вращающейся детали переводят в неподвижную точку. Такое уравновешивание применяется для плоских деталей, длина которых мала по сравнению с диаметром. Если такую деталь заменить сосредоточенной массой m, вращающейся относительно неподвижного центра вращения (рис. 100, а), то можно записать уравнение динамики:
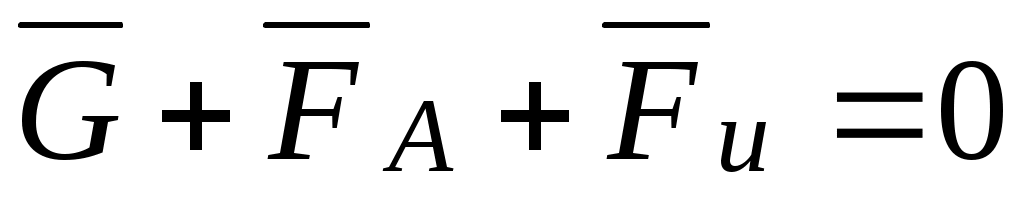 ,
,
г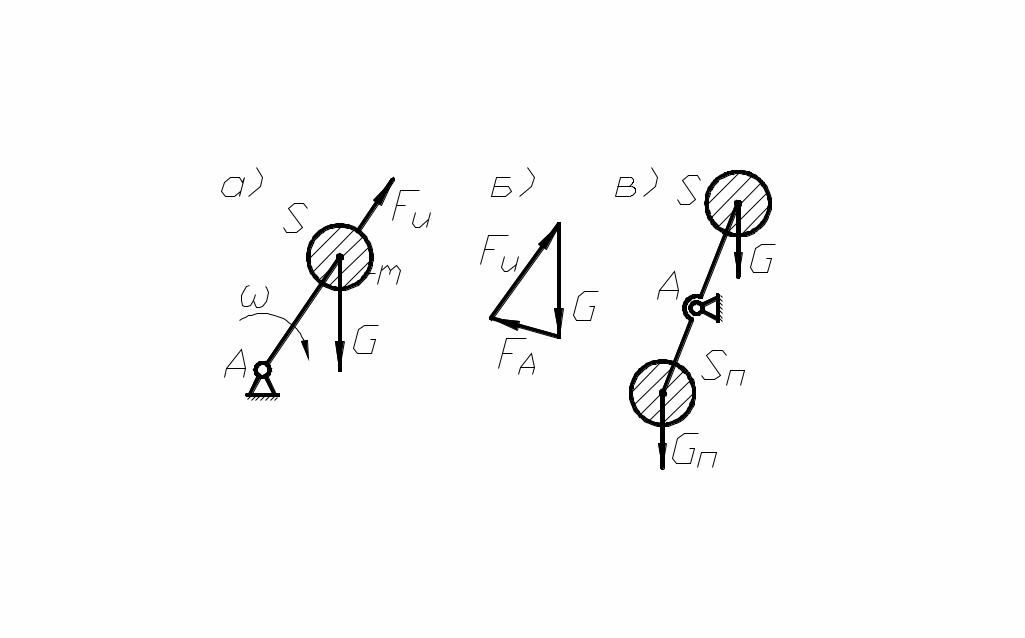 де G – вес; FA – реакция в опоре;
де G – вес; FA – реакция в опоре;
Fu – сила инерции, равная:
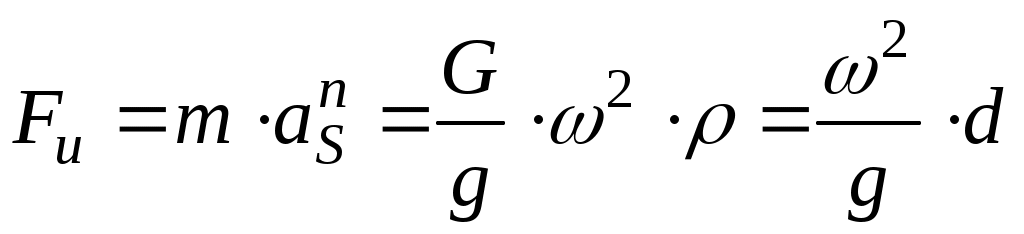 .
.
Здесь g– ускорение силы тяжести;
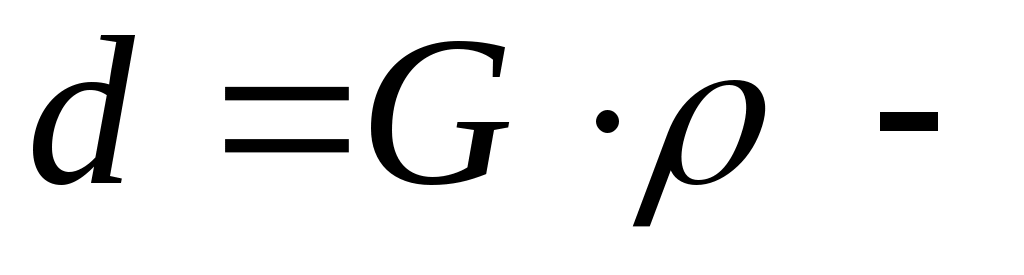 дисбаланс (
дисбаланс (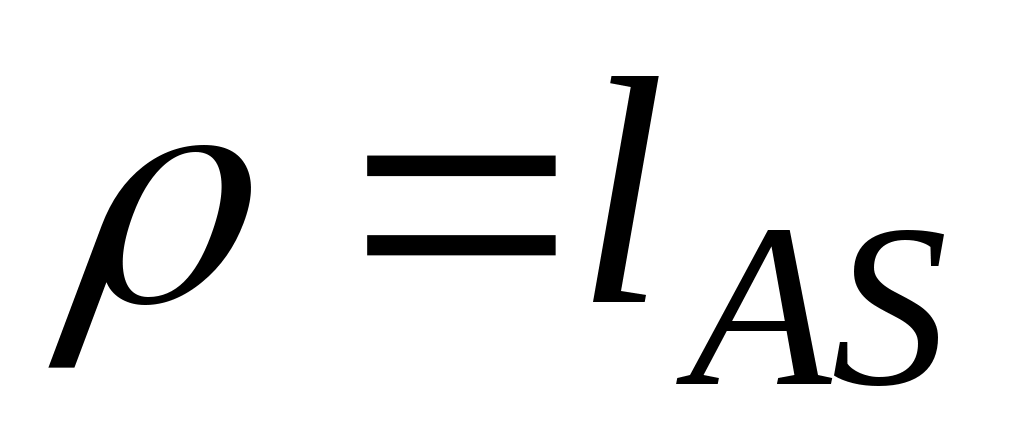 ), который характеризует неуравновешенность и направлен так же
), который характеризует неуравновешенность и направлен так же
рис. 100 как сила инерции Fu.
План сил в данном положении (рис. 100, б) показывает, что FA – величина переменная по направлению и создаёт динамические нагрузки и вибрацию. Если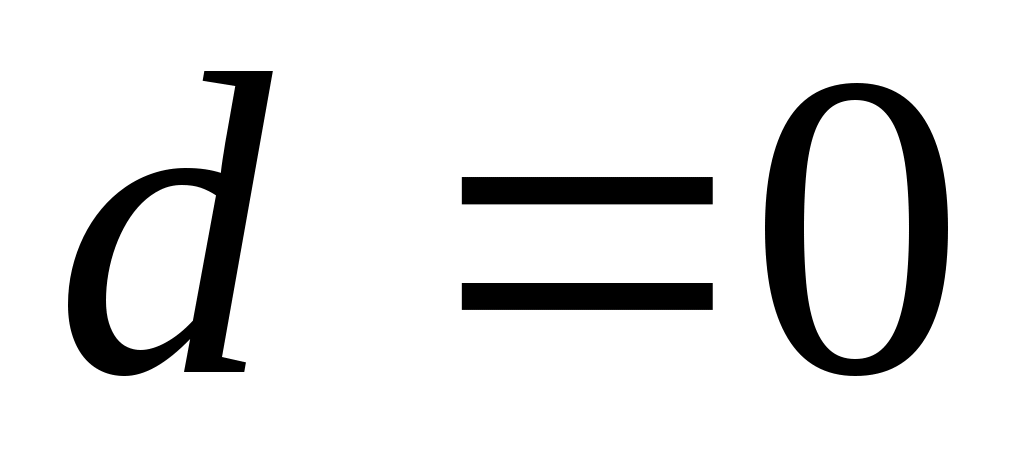 , то
, то 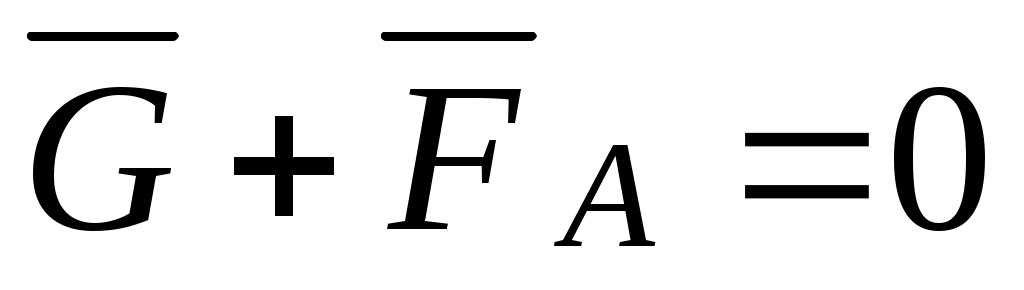 и динамические нагрузки отсутствуют. Для этого необходимо уравновесить дисбаланс установкой массы противовеса с противоположной стороны (рис. 100, в). Тогда дисбалансы будут уравновешены и Gп определяется из условия
и динамические нагрузки отсутствуют. Для этого необходимо уравновесить дисбаланс установкой массы противовеса с противоположной стороны (рис. 100, в). Тогда дисбалансы будут уравновешены и Gп определяется из условия 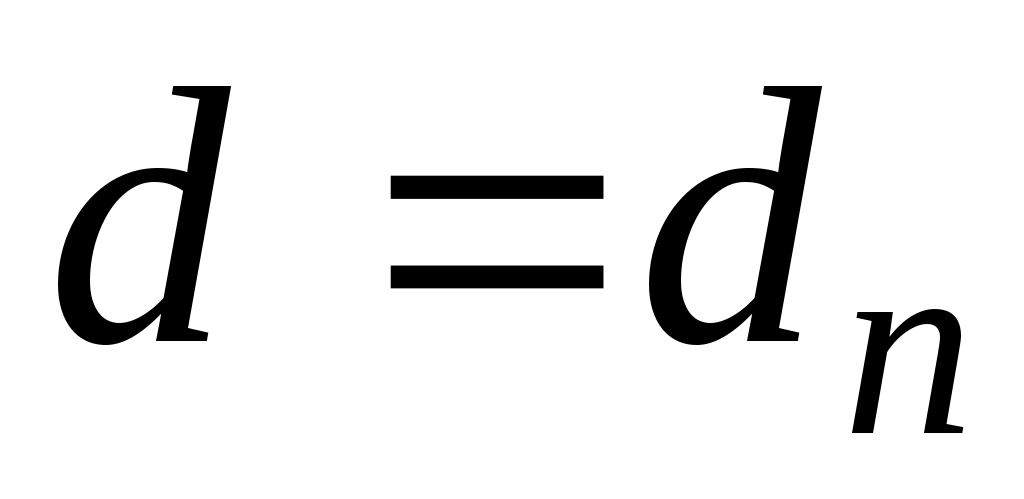
, т.е.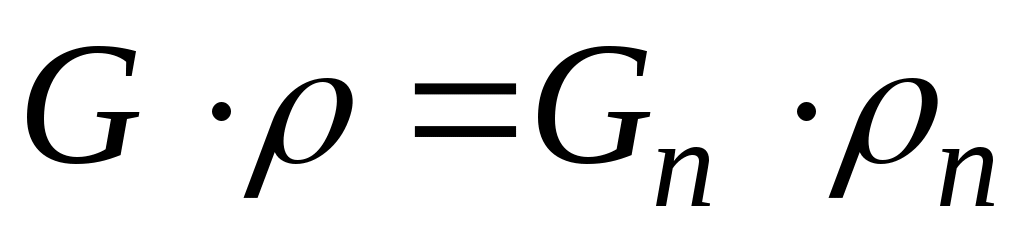 , где
, где 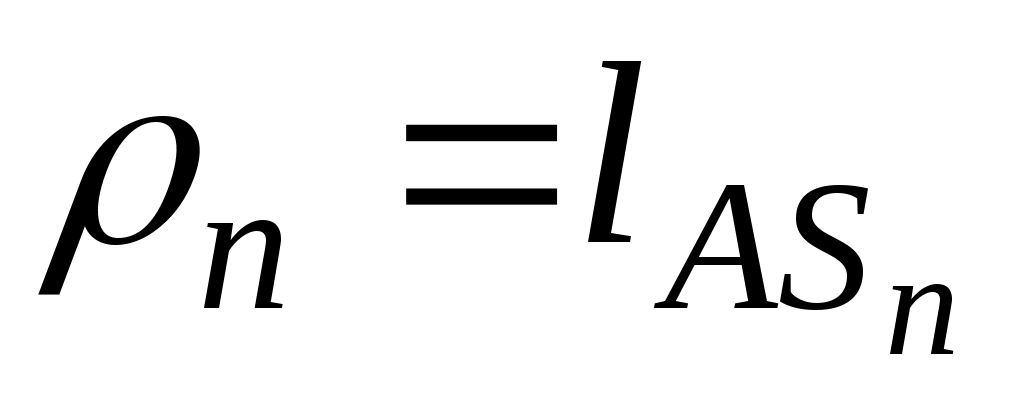 .
.
Рассмотрим уравновешивание неплоской детали, которую можно представить, например, в виде двух грузов G1 и G2 (рис. 101, а). В этом случае возникают
реакции, вызванные неуравновешенностью как сил, так и моментов от сил инерции. Причём момент от сил инерции относительно точки А равен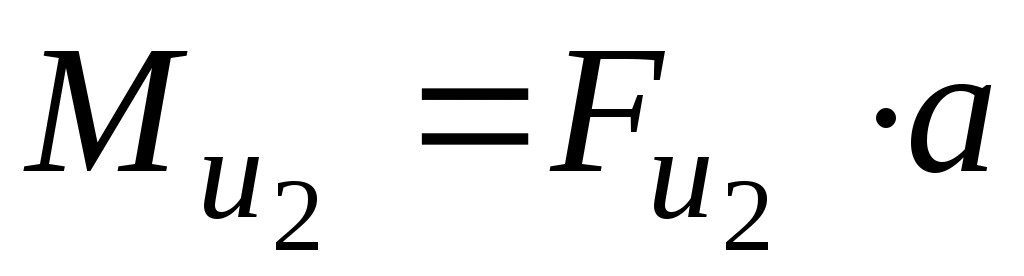 и характеризуется дисбалансом
и характеризуется дисбалансом 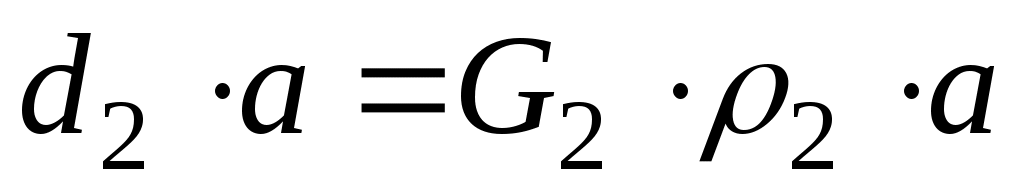 .
.
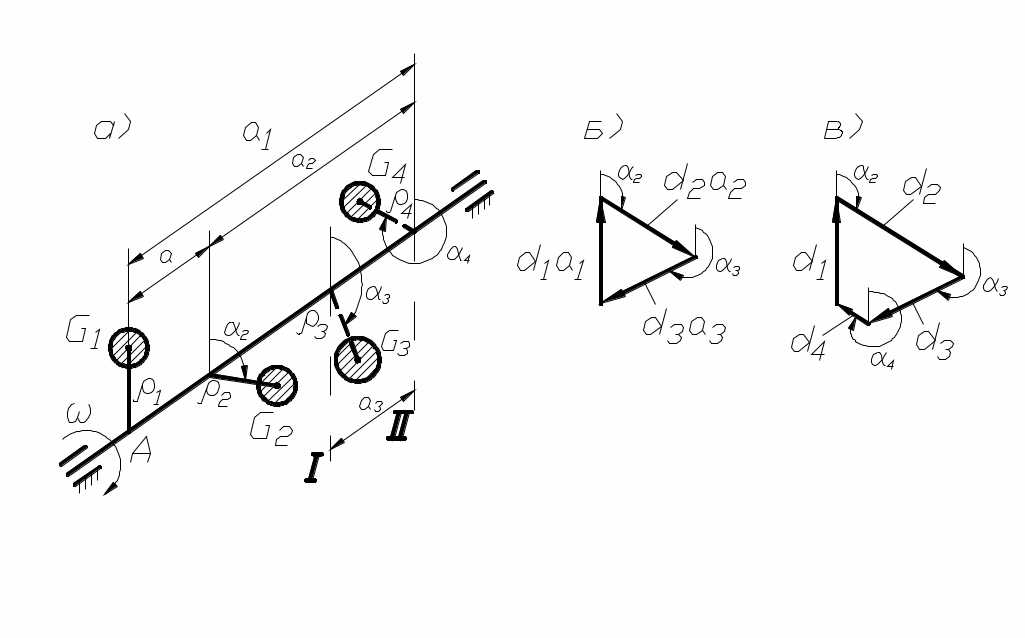
рис. 101
В этом случае динамические нагрузки на опоры возникают даже если проведена статическая балансировка, когда центр тяжести грузов 1 и 2 совпадает с центром вращения. Уравновешивание моментов от сил инерции вращающихся деталей будет обеспечена динамической балансировкой.
Полное уравновешивание системы можно осуществить двумя дополнительными грузами G3 и G4, установленными в разных плоскостях I и II, называемых плоскостями исправления. При этом должны выполняться условия:
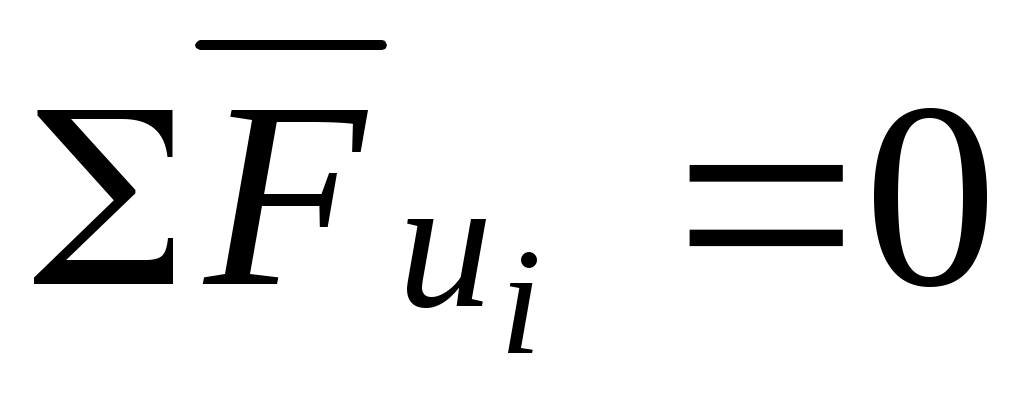 или
или 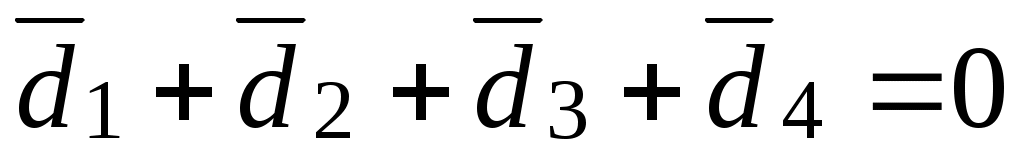 ;
;
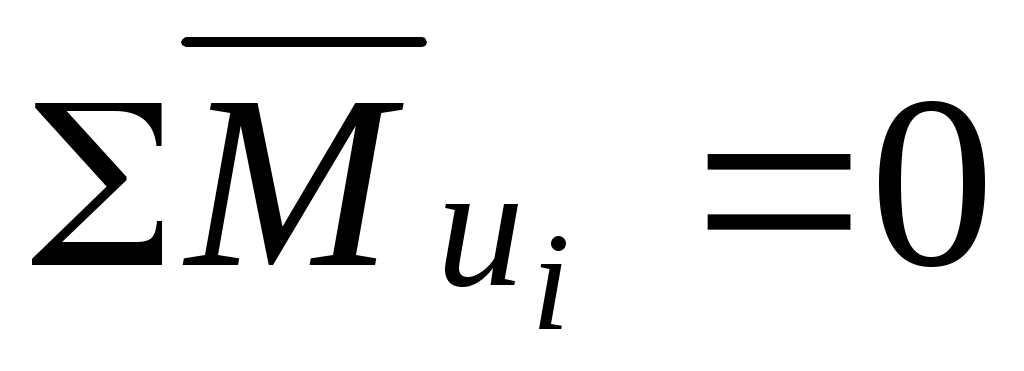 или
или 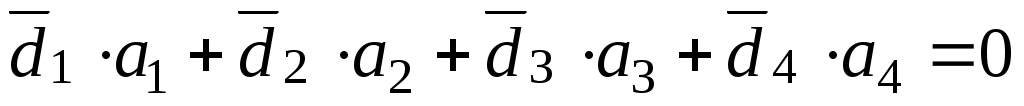 .
.
Совместное решение указанных уравнений, например, графическим путём (рис. 101, б, в) позволяет найти вес и положение противовесов G3 и G4.
Балансировка вращающихся масс осуществляется на специальных балансировочных станках, при этом исключается неуравновешенность, вызванная неточностью изготовления детали.
Список книг по дисциплине “Теория механизмов и машин”
1. Артоболевский И. И. ТММ./учебник для вузов/.-4-е изд., перераб. и доп.-М.: Наука, 1988.
2. Артоболевский И. И. Сборник задач по ТММ./для машин. Спец.вузов/2-е изд., стереотипное.-М.:Наука, 1975,1973.
3. Баранов Г. Г. Курс ТММ./для авиац. спец. вузов/.Изд. 5-е, стереотип.-М.: Машиностроение, 1975.
4. Безвесельный Е. С. Курсовое проектирование по ТММ в примерах. -Харьков: изд-во Харьк.ун-та, 1960.
5. Безвесельный Е. С. Вопросы и задачи по ТММ:-Киев, 1977.
6. Белоконев И. М. ТММ: Методы автоматизированного проектирования. Уч. пособие для техн.вузов.-Киев:Выща школа, 1990.
7. Ковалев Н. А. ТММ и детали машин. Краткий курс/для немашин. спец. вузов/изд-е 2-е, испр.-М.: Высш.шк., 1973.
8. Кореняко А. С. ТММ. Учебник для втузов. Изд.3-е, перераб.-Киев:Выща Щкола, 1976.
9. Курсовое проектирование по ТММ./Уч.пособие для инж.-техн.спец.вузов/ Под редакцией Г. Н. Девойно-Минск: 1986.
10. Курсовое проектирование по ТММ. Уч.пособие для механ. И машиностр. Спец. вузов. Под ред. А. С. Кореняко-М.-Л.:Машин-е, 1964, 1970.
11. Левитская О. Н., Левитский Н. И. Курс ТММ./Уч.пособие для механ.спец. вузов/ 2-е изд., перераб. и доп.-М.:Наука, 1990.
12. Машнев М. М. ТММ и детали машин./Уч.пособие для немашин.спец. вузов/2-е изд., перераб. и доп., Л.: Машин-е,1980.
13. ТММ. Проектирование./Уч.пособие для машин. Спец. вузов/Под общей редакцией О. Н. Кульбачного.-1970.
14. ТММ. Сборник контрольных работ и курсовых проектов. Под общей ред. Н. В. Алехновича. Уч.пособие для студ.-заочников механ.спец.вузов-Минск: Выща шк., 1970.
15. ТММ и механика машин. Учебник для вузов. Под ред. Фролова К. В. 2-е изд., перераб. и доп.-М.: Высшая школа, 1998.
16. ТММ./ Учебник для вузов/Под ред. Фролова К. В.-1987.
17. Юдин В. А., Петрокас Л. В. ТММ: Учебник,2-е изд.,перераб. и доп.-М.: Высшая школа, 1977.
рис. 97 моментном (динамическом) уравновешивании, которое называется уравновешиванием второго рода.
10.2. Уравновешивание с помощью противовесов на звеньях механизма
Рассмотрим последовательность статического уравновешивания на примере четырёхшарнирного механизма (рис. 98, а). Заменяем массы звеньев 1, 2, 3 сосредоточенными массами в точках A, B, C, D, причём в силу неподвижности точек A и D, массы, сосредоточенные в этих точках, можно не учитывать.
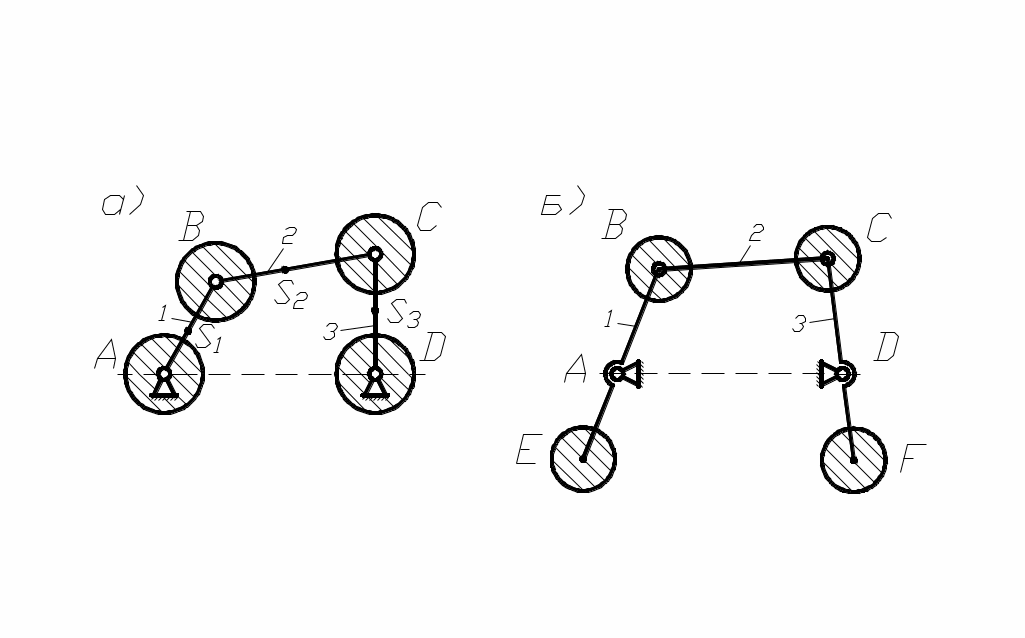
рис. 98
Приведённые массы в точках В и С равны:
Так как заменяющие массы mB и mC совершают вращательное движение, то для уравновешивания сил инерции необходимы противовесы с массами mЕ и mF, определяемыми из условий (рис. 98, б):
где, задавая длины противовесов, можно получить их массы и наоборот.
Рассмотрим моментное уравновешивание на примере четырёхшарнирного механизма. Его приближённое моментное уравновешивание можно осуществить после статического уравновешивания, введя в схему механизма два одинаковых дополнительных противовеса
 соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой скоростью
соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой скоростью рис. 99 вращается с той же угловой скоростью
равен
10.3. Уравновешивание вращающихся масс (роторов)
Ротором в теории балансировки называется любое вращающееся тело. В связи с появлением быстроходных машин возникла проблема уравновешивания быстровращающихся деталей. Так, например, скорость некоторых турбин, валов гироскопов, суперцентрифуг достигает 3÷50 тысяч об/мин и малейшее смещение центра масс с геометрической оси вращения вызывает появление больших сил инерции, т.е. вибрационных явлений в машине и фундаменте.
Различают статическое уравновешивание (статическая балансировка) вращающихся роторов и динамическое. Статическая балансировка достигается тем, что центр тяжести вращающейся детали переводят в неподвижную точку. Такое уравновешивание применяется для плоских деталей, длина которых мала по сравнению с диаметром. Если такую деталь заменить сосредоточенной массой m, вращающейся относительно неподвижного центра вращения (рис. 100, а), то можно записать уравнение динамики:
г
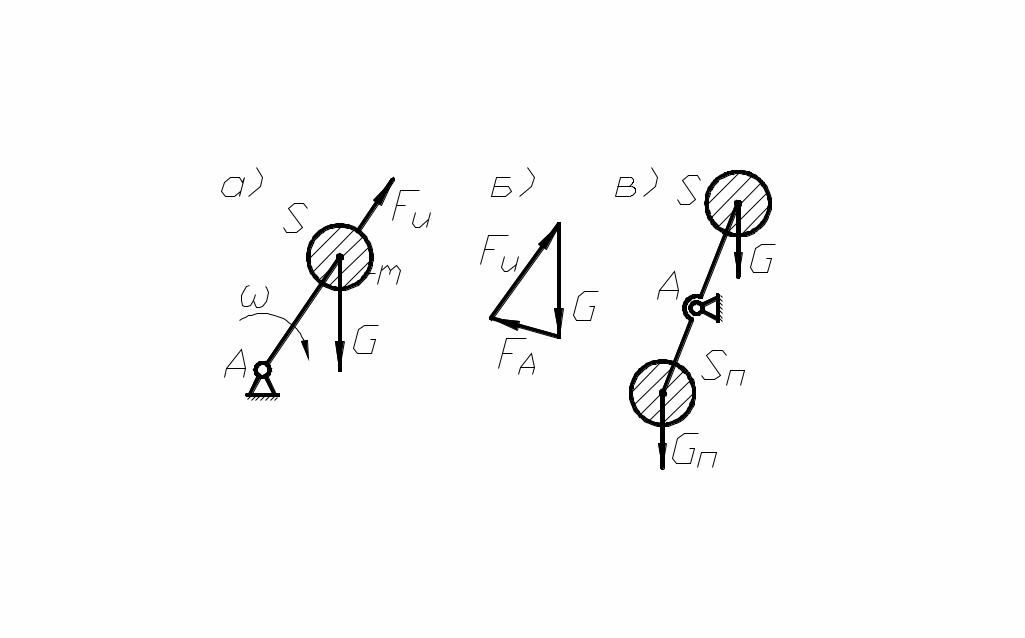 де G – вес; FA – реакция в опоре;
де G – вес; FA – реакция в опоре; Fu – сила инерции, равная:
Здесь g– ускорение силы тяжести;
рис. 100 как сила инерции Fu.
План сил в данном положении (рис. 100, б) показывает, что FA – величина переменная по направлению и создаёт динамические нагрузки и вибрацию. Если
, т.е.
Рассмотрим уравновешивание неплоской детали, которую можно представить, например, в виде двух грузов G1 и G2 (рис. 101, а). В этом случае возникают
реакции, вызванные неуравновешенностью как сил, так и моментов от сил инерции. Причём момент от сил инерции относительно точки А равен

рис. 101
В этом случае динамические нагрузки на опоры возникают даже если проведена статическая балансировка, когда центр тяжести грузов 1 и 2 совпадает с центром вращения. Уравновешивание моментов от сил инерции вращающихся деталей будет обеспечена динамической балансировкой.
Полное уравновешивание системы можно осуществить двумя дополнительными грузами G3 и G4, установленными в разных плоскостях I и II, называемых плоскостями исправления. При этом должны выполняться условия:
Совместное решение указанных уравнений, например, графическим путём (рис. 101, б, в) позволяет найти вес и положение противовесов G3 и G4.
Балансировка вращающихся масс осуществляется на специальных балансировочных станках, при этом исключается неуравновешенность, вызванная неточностью изготовления детали.
Список книг по дисциплине “Теория механизмов и машин”
1. Артоболевский И. И. ТММ./учебник для вузов/.-4-е изд., перераб. и доп.-М.: Наука, 1988.
2. Артоболевский И. И. Сборник задач по ТММ./для машин. Спец.вузов/2-е изд., стереотипное.-М.:Наука, 1975,1973.
3. Баранов Г. Г. Курс ТММ./для авиац. спец. вузов/.Изд. 5-е, стереотип.-М.: Машиностроение, 1975.
4. Безвесельный Е. С. Курсовое проектирование по ТММ в примерах. -Харьков: изд-во Харьк.ун-та, 1960.
5. Безвесельный Е. С. Вопросы и задачи по ТММ:-Киев, 1977.
6. Белоконев И. М. ТММ: Методы автоматизированного проектирования. Уч. пособие для техн.вузов.-Киев:Выща школа, 1990.
7. Ковалев Н. А. ТММ и детали машин. Краткий курс/для немашин. спец. вузов/изд-е 2-е, испр.-М.: Высш.шк., 1973.
8. Кореняко А. С. ТММ. Учебник для втузов. Изд.3-е, перераб.-Киев:Выща Щкола, 1976.
9. Курсовое проектирование по ТММ./Уч.пособие для инж.-техн.спец.вузов/ Под редакцией Г. Н. Девойно-Минск: 1986.
10. Курсовое проектирование по ТММ. Уч.пособие для механ. И машиностр. Спец. вузов. Под ред. А. С. Кореняко-М.-Л.:Машин-е, 1964, 1970.
11. Левитская О. Н., Левитский Н. И. Курс ТММ./Уч.пособие для механ.спец. вузов/ 2-е изд., перераб. и доп.-М.:Наука, 1990.
12. Машнев М. М. ТММ и детали машин./Уч.пособие для немашин.спец. вузов/2-е изд., перераб. и доп., Л.: Машин-е,1980.
13. ТММ. Проектирование./Уч.пособие для машин. Спец. вузов/Под общей редакцией О. Н. Кульбачного.-1970.
14. ТММ. Сборник контрольных работ и курсовых проектов. Под общей ред. Н. В. Алехновича. Уч.пособие для студ.-заочников механ.спец.вузов-Минск: Выща шк., 1970.
15. ТММ и механика машин. Учебник для вузов. Под ред. Фролова К. В. 2-е изд., перераб. и доп.-М.: Высшая школа, 1998.
16. ТММ./ Учебник для вузов/Под ред. Фролова К. В.-1987.
17. Юдин В. А., Петрокас Л. В. ТММ: Учебник,2-е изд.,перераб. и доп.-М.: Высшая школа, 1977.