б) разработка эскизного проекта, включающего выбор схемы и компоновку основных узлов конструкции;

в) разработка технического проекта, где осуществлены основные расчеты и представлены сборочный чертеж и др. документация.

При проектировании сложных механизмов обычно стремятся выделить из общей схемы отдельные, более простые типовые механизмы, проектирование которых имеет свои закономерности. К таким широко используемым в технике механизмам относятся: рычажные (стержневые), кулачковые, фрикционные, зубчатые и др., причем с точки зрения строения, кинематики и динамики любой механизм можно заменить условным рычажным механизмом с последующим его анализом, поэтому структура, кинематика и динамика рычажных механизмов рассматривается наиболее подробно.
3. Структурная классификация и виды механизмов

3.1. Классификация кинематических пар




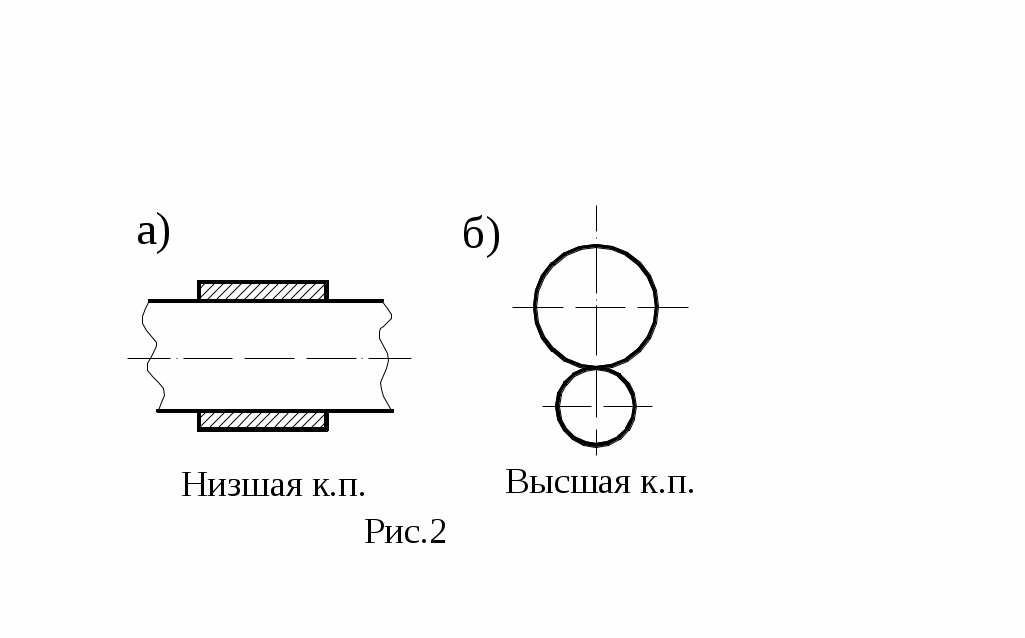
Подвижные соединения двух звеньев, называемые кинематической парой (к.п.), классифицируются по разным признакам, например, по характеру соприкосновения звеньев – на низшие, когда контакт происходит по поверхности, и высшие, когда контакт звеньев осуществляется по линии или в точке (рис.2, а, б).

Преимуществом низших к.п. является возможность передачи значительных усилий при малом износе, а достоинством высших к.п. возможность воспроизводить достаточно сложные относительные движения.


Низшие к.п. могут быть поступательными, вращательными, плоскими и пространственными, а также классифицироваться по числу условий связи, накладываемых на звенья при соединении их в к.п.

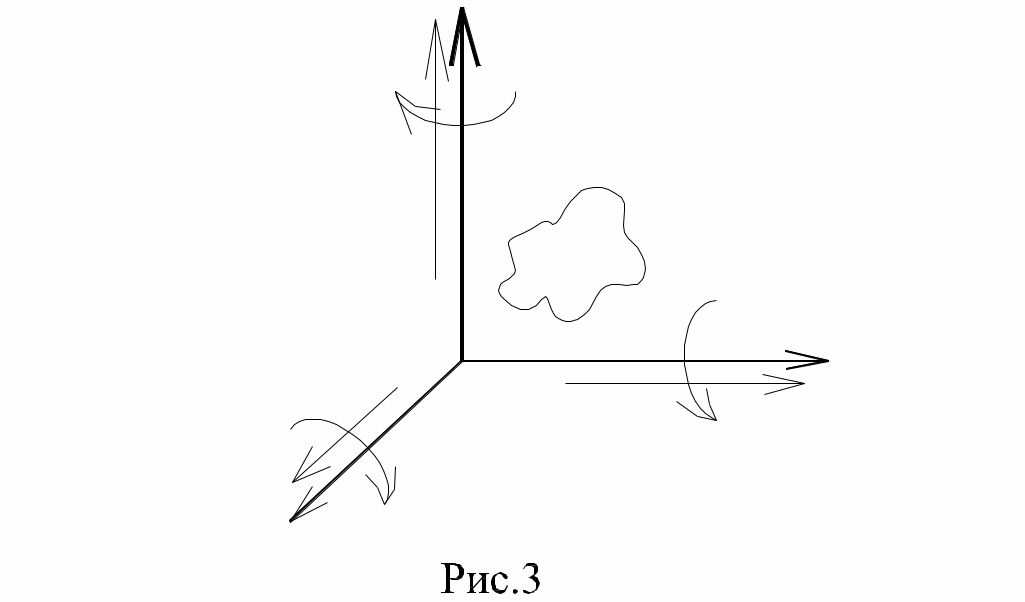
Любое тело в декартовой системе координат (рис.3) имеет 6 степеней свободы или подвижности (W=6), часть из которых уничтожается в к.п., при этом класс к.п. определяется числом накладываемых связей (6-S),

где S – число относительных движений звеньев в к.п. Например, на рис. 4а-д

п
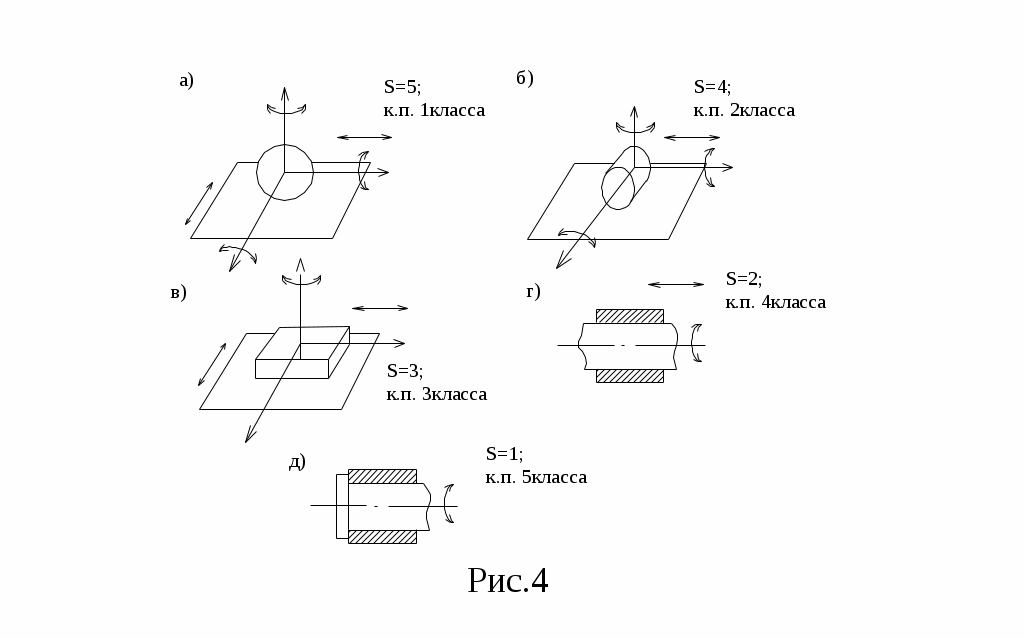
риведены к.п. различных классов.
К 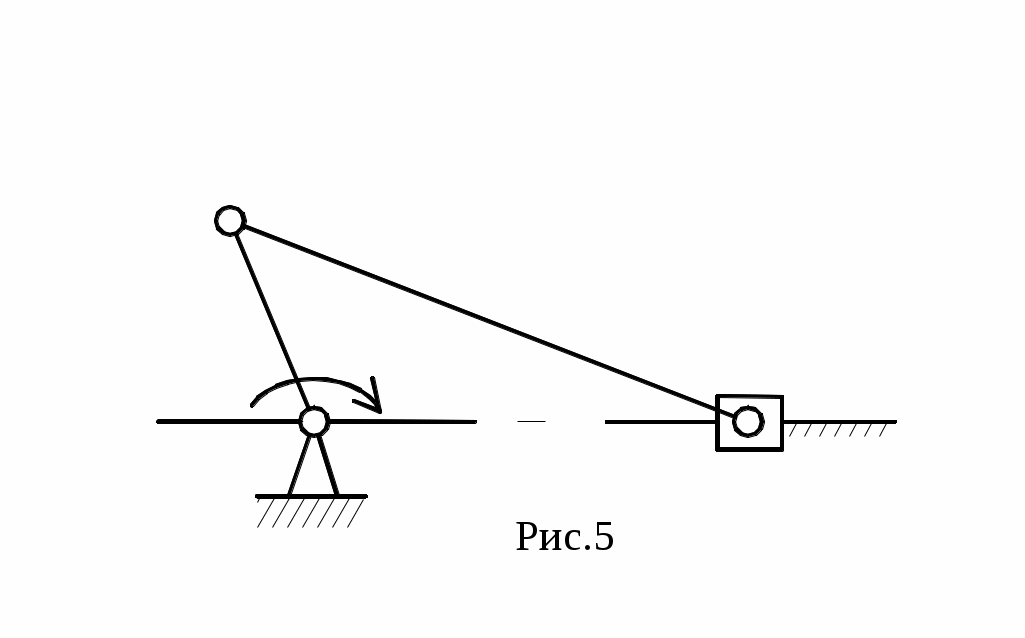инематические пары и звенья механизмов изображаются упрощенно (рис.5) при соблюдении ГОСТа на обозначения звеньев и к.п.

---

3.2. Кинематические цепи и их классификация
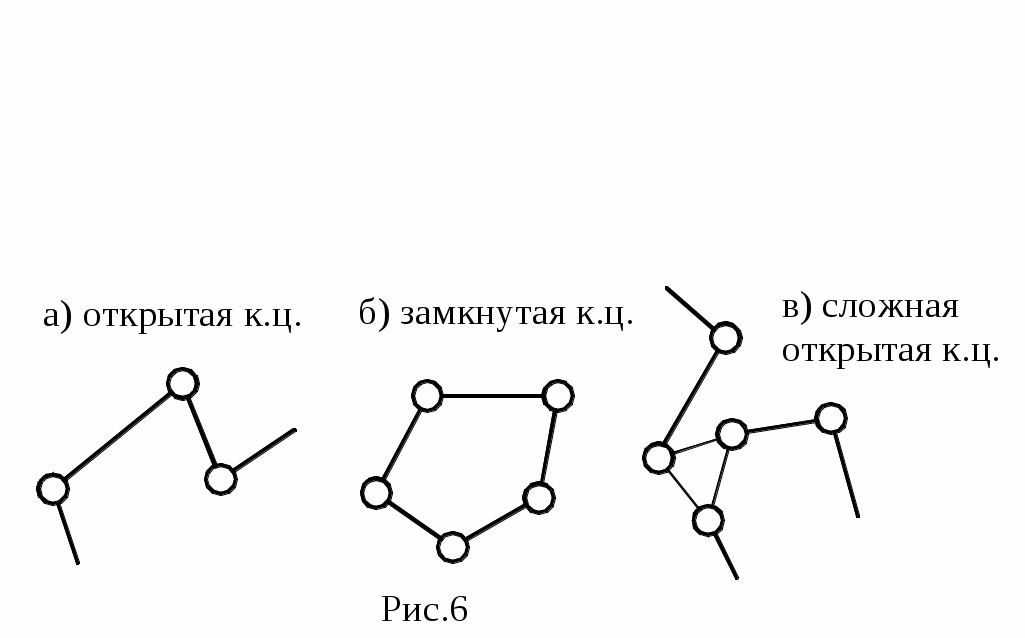
Любой механизм представляет собой кинематическую цепь (к.ц.) звеньев, соединенных в кинематические пары (к.п.). К.ц. могут быть простыми и сложными, открытыми и замкнутыми, плоскими и пространственными.

В простой к.ц. каждое из ее звеньев входит в состав одной или двух к.п., а в сложной к.ц. имеются звенья, входящие в состав трех и более к.п.


а) простая

открытая к.ц.

б) простая

замкнутая к.ц.

в) сложная

открытая к.ц.
В открытой к.ц. имеются звенья, входящие в состав одной к.п., а в замкнутой цепи каждое звено входит в состав 2-х и более к.п. (рис.6,а-в).





Если точки всех звеньев двигаются в одной или параллельных плоскостях, то к.ц. называется плоской, в противном случае к.ц. – пространственная (точки звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые).
3.3. Понятие о степени подвижности механизма
Если в пространственной к. ц., состоящей из «n» подвижных звеньев, имеются к.п. 1-ого, 2-ого,… 5-ого класса, число которых, соответственно, p₁,p₂,… p₅, то к. ц. имеет число степеней свободы, определяемое формулой А.П. Малышева.

W=6n-5p₅-4p₄-3p₃-2p₂-p₁ (3.1)

Так как любой механизм имеет одно неподвижное звено (стойку) и «n» подвижных звеньев, то формула (3.1) может использоваться для определения W пространственного механизма, где n – число подвижных звеньев, а W – степень подвижности механизма, показывающая сколько нужно иметь ведущих звеньев (двигателей) для получения определенного движения остальных его звеньев.

Для плоского механизма степень подвижности определяется по формуле Чебышева:

W=3n-2p₅-p₄, (3.2)

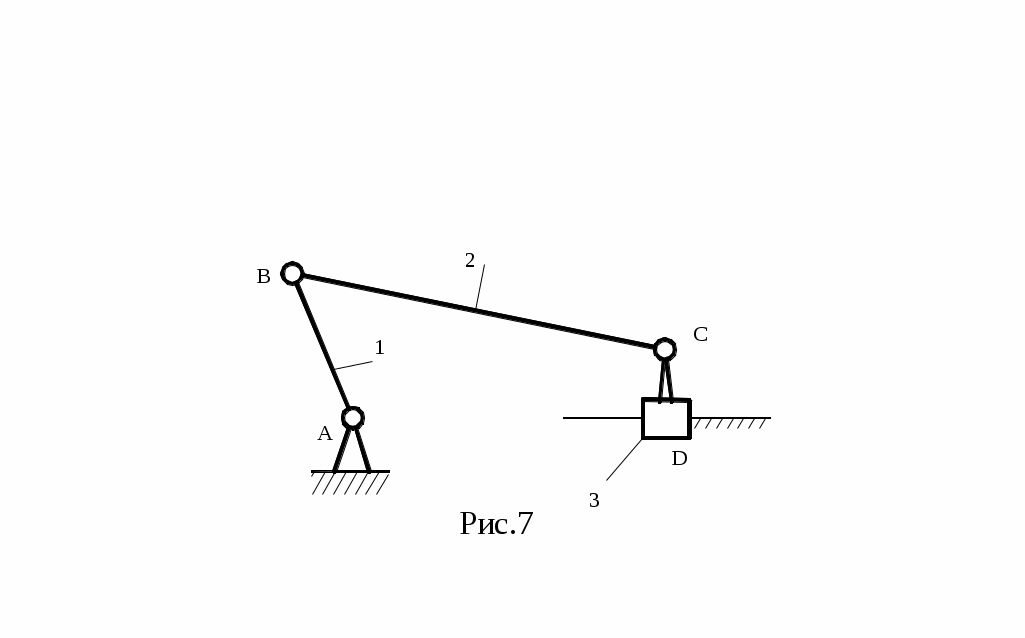При этом к.п. 5-ого класса существует в виде поступательных, вращательных и винтовых.

Например, кривошипно-ползунный плоский меха-низм (рис.7), в котором n=3; p₅=4; p₄=0,

имеет W=3·3-2·4-0=1.




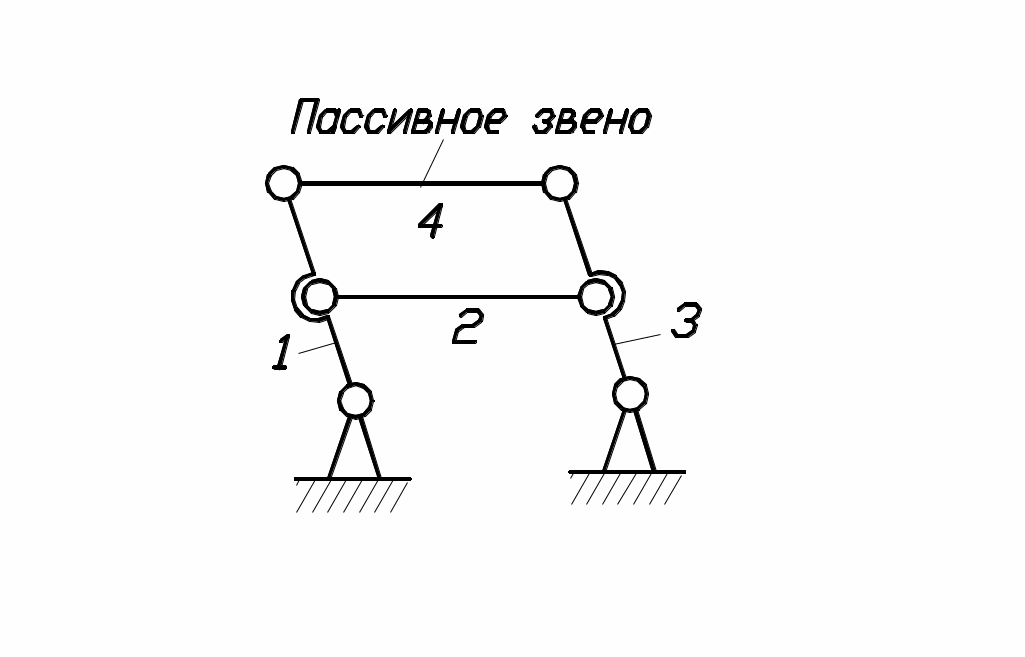
При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т.е. звеньев, устраняемых без формального ущерба для кинематики анализируемого механизма (рис.8).

---

а) W=3·4-2·6-0=0 – с пассивным звеном,

б) W=3·3-2·4-0=1 – фактически.

Кроме того, необходимо учитывать возможность наличия избыточных связей,

Рис. 8 которые не реализуются в реальном механизме, а их число q определяется разностью между числом связей в к.п. действительного и формально возможного механизмов.

На рис. 9, а показан действительный механизм, а на рис. 9, б – формально возможный механизм, имеющий функциональное назначение, аналогичное действительному механизму, но где все связи, в отличие от действительного механизма, реализованы.


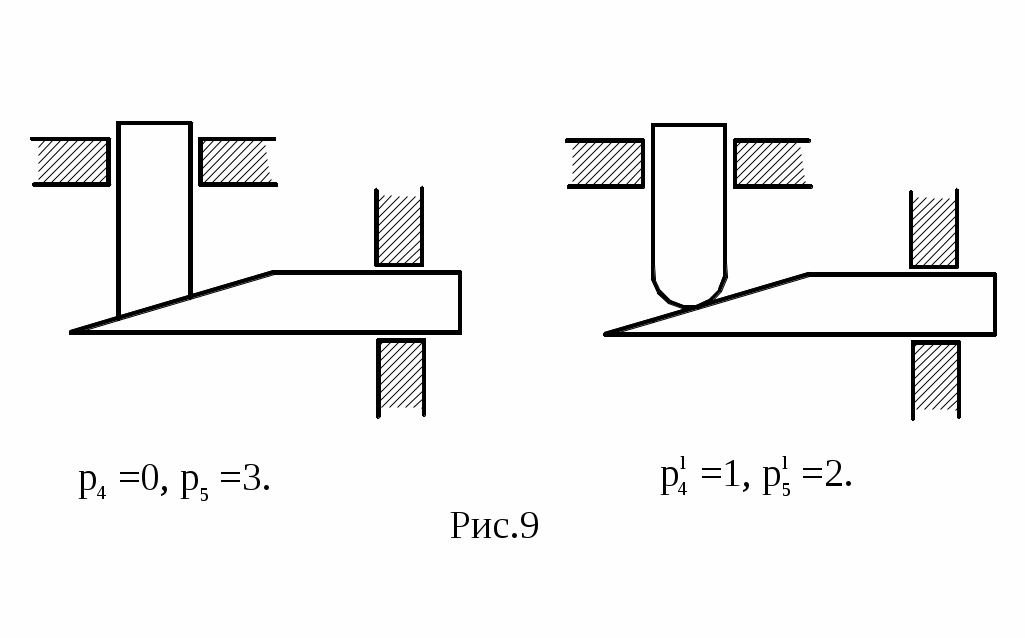
Число избыточных связей q в действительном механизме равно:

q=(2p₅+p₄)-(2p^/₅+p^/₄)=(2·3+0)-(2·2+1)=1,

т.е. степень подвижности действительного механизма равна:

W=3n-2p₅-p₄+q=3·2-2·3-0+1=1.

В общем случае пространственного механизма:

W=6n-i·p_i+q, (i от 1 до 5).

---

3.4. Структурный анализ механизмов

Основной принцип образования рычажных механизмов был сформулирован в 1914 году профессором Л. В. Ассуром и заключается в следующем.

Схема любого механизма может быть составлена последовательным присоединением к входным (начальным) звеньям и стойке к.ц. с нулевой степенью подвижности. Такие к. ц. называются структурными группами Ассура. Примеры различных групп Ассура показаны на рис.10.

Начальное звено со стойкой образует простейший механизм 1-ого класса (рис.11).

Путем присоединения к таким механизмам различных групп Ассура можно получить механизм любой сложности.

Группы Ассура классифицируются по числу к.п., которыми они присоединяются к основному механизму. Это число определяет порядок группы. Кроме того, группа Ассура имеет класс, определяемый числом к.п., образующих наиболее сложный замкнутый контур.








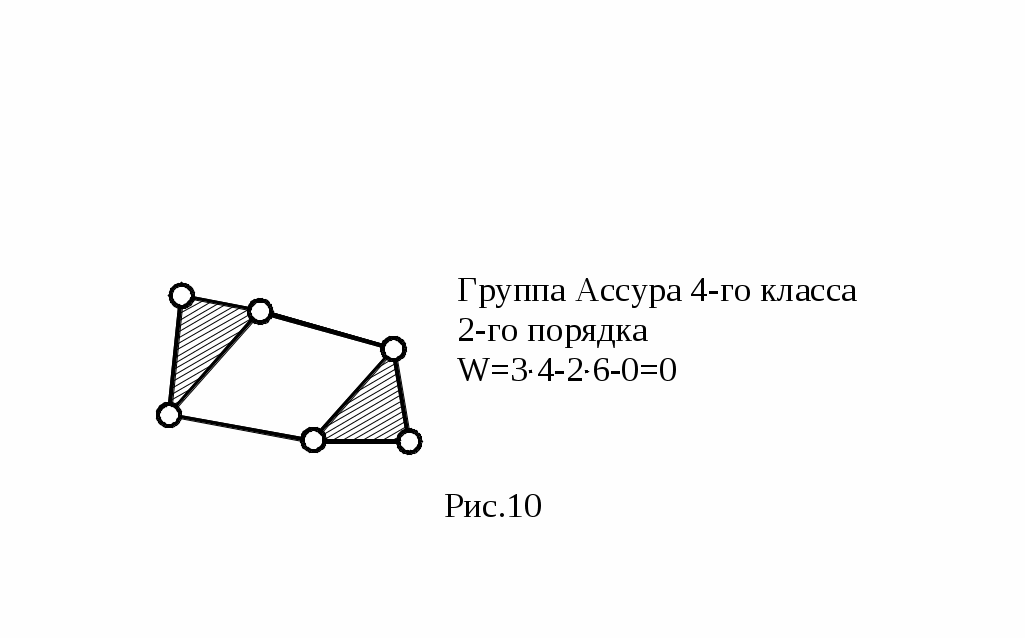
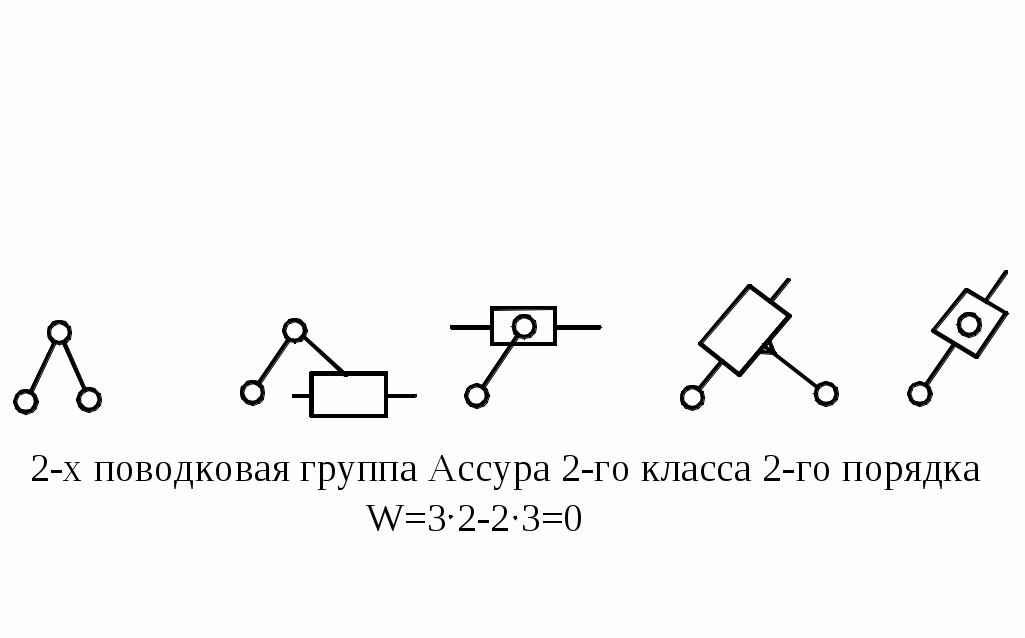
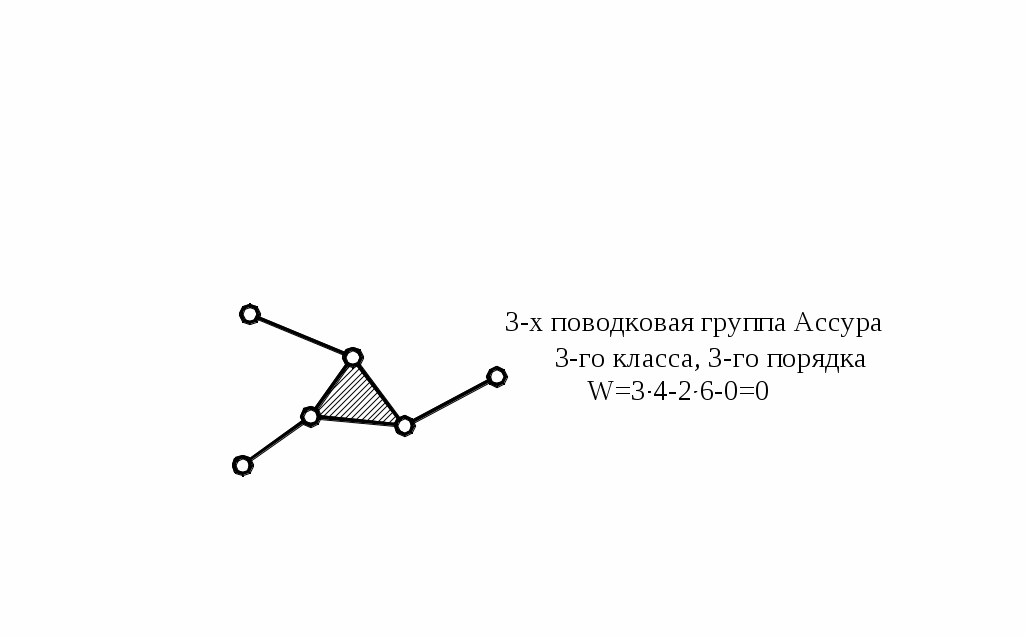
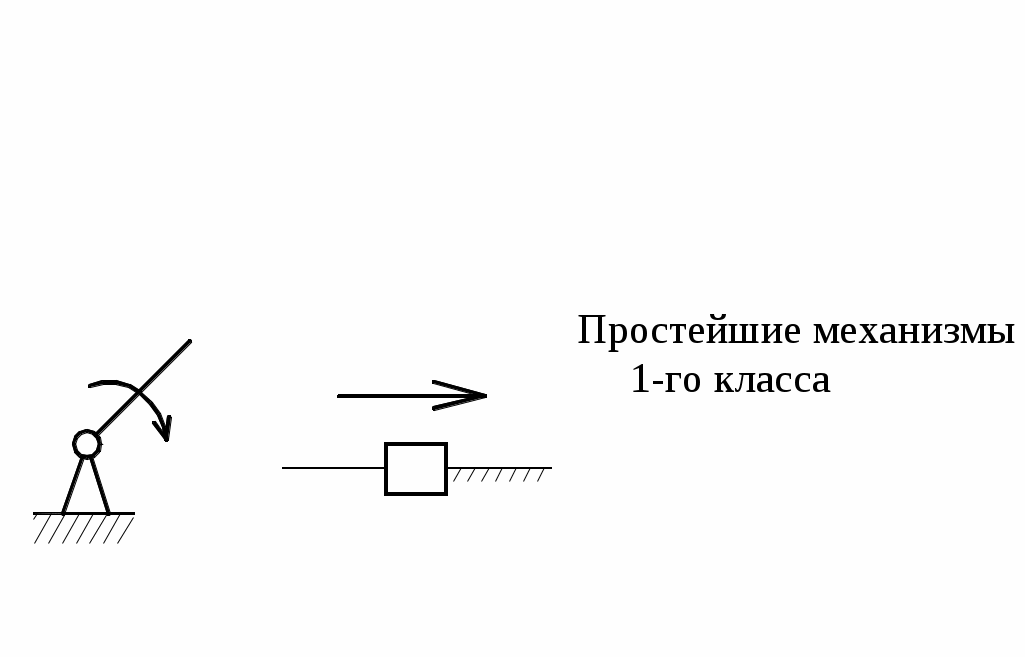
Рис. 11

С
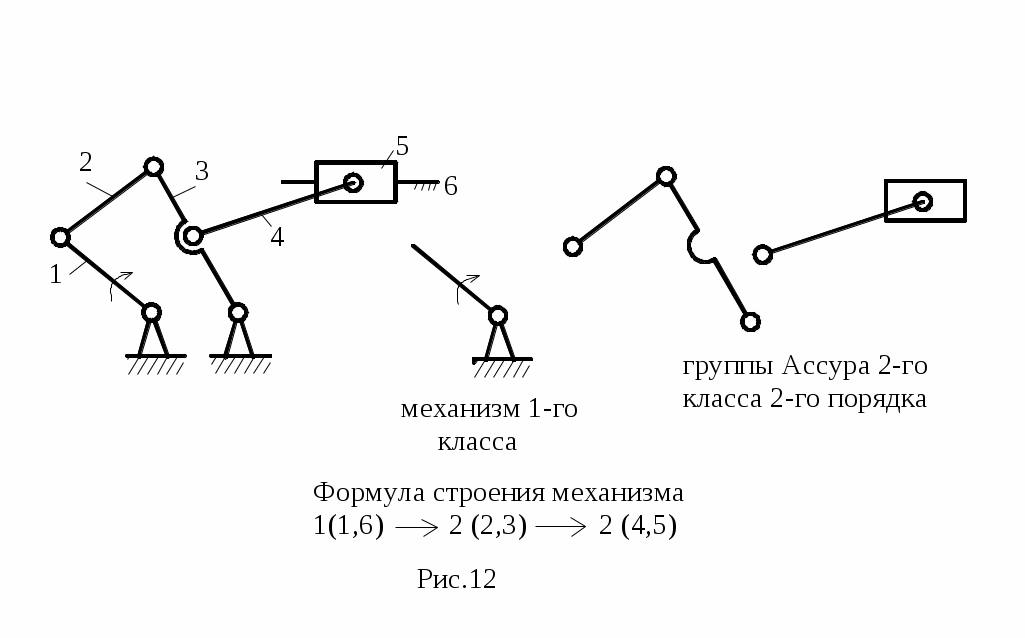
остав и последовательность присоединения групп Ассура в механизме можно выразить его формулой строения. Механизм в целом классифицируется по группе наивысшего класса. На рис.12 показан пример такой классификации.
3.5. Виды механизмов и их структурные схемы
Среди всего многообразия конструкций механизмов различают: стержневые (рычажные), кулачковые, фрикционные, зубчатые механизмы, механизмы с гибкими звеньями (например, ременные передачи) и др. виды.

Менее распространенные классификации подразумевают наличие механизмов с низшими или высшими парами в плоском или пространственном исполнении и т.д.


Учитывая возможность условного превращения практически любого механизма с высшими парами в рычажный, в дальнейшем наиболее подробно рассматривается именно эти механизмы, а структурные схемы других механизмов изложены в соответствующих разделах.

---

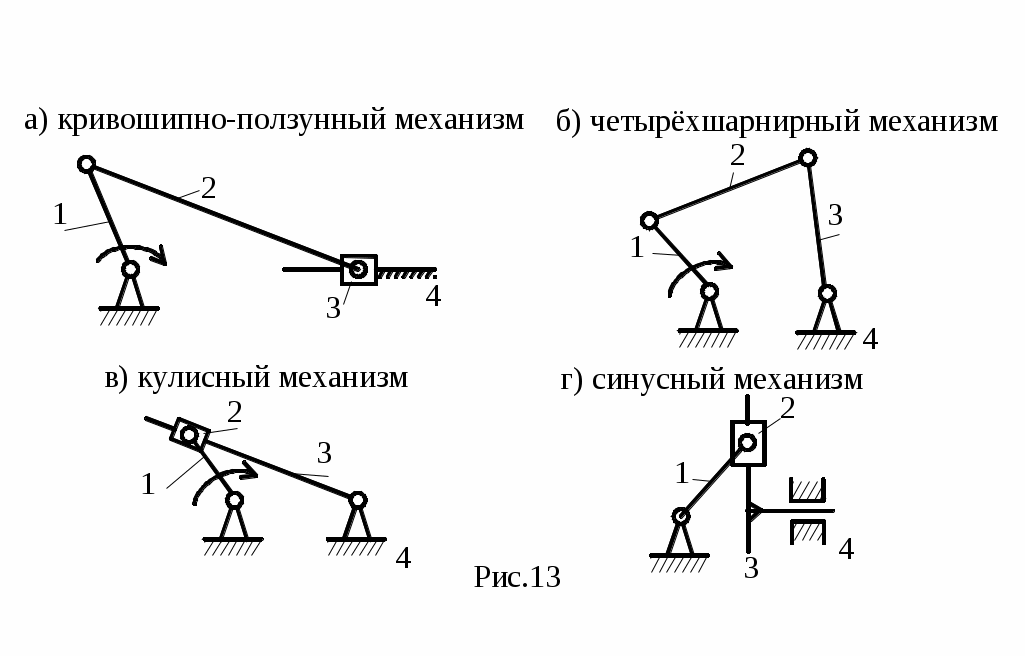
Среди рычажных механизмов наиболее распространенны так называемые четырехзвенные, примеры которых представлены на рис.13, а-г.

В этих механизмах встречаются однотипные звенья: кривошип – звено, совершающее полнооборотное вращательное движение вокруг неподвижной оси; коромысло – звено, совершающее неполнооборотное вращательное движение вокруг неподвижной оси; ползун – звено, совершающее поступательное движение относительно стойки; камень – звено, совершающее поступательное движение относительно подвижной направляющей, называемой кулисой; шатун – звено, совершающее плоскопараллельное движение.
4. Кинематический анализ рычажных механизмов
Кинематический анализ механизмов включает вопросы изучения звеньев с геометрической точки зрения, т.е. без учета действующих сил. Для этого используются графические, аналитические и экспериментальные методы исследования.

Одним из наглядных методов является графоаналитический, который включает:

а) построение планов положения механизма; б) определение скоростей и ускорений характерных точек или звеньев механизма.

При графических построениях на чертеже изображаются длины звеньев, скорости, ускорения и др. величины в определенном масштабе, характеризуемом масштабным коэффициентом:

=значение параметра/длина отрезка.

Например, вектор pa длиной 10 мм изображает скорость V=20 м/с. Тогда _v=20/10=2 м·с^-1/мм.
4.1. Построение планов положения механизма
Графическое изображение взаимного расположения звеньев механизма, соответствующее заданному моменту времени, называется планом положений или планом механизма.

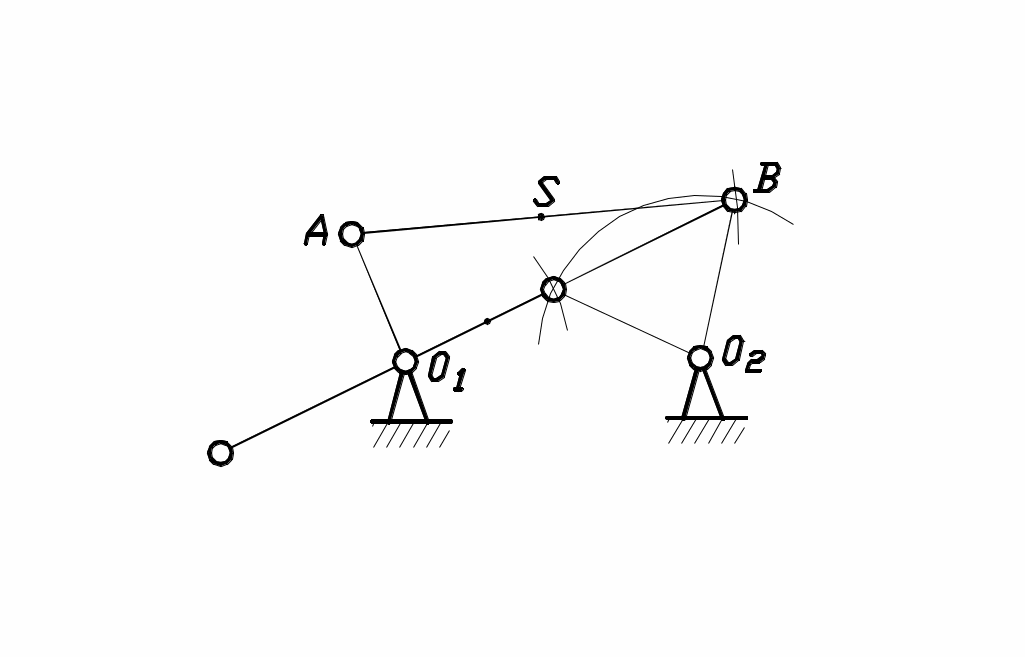Планы положения строятся в определенном масштабе методом засечек в соответствии с формулой строения механизма, При этом должны быть заданы линейные размеры всех звеньев (рис.14).

После построения нескольких совмещенных планов механизма

Рис. 14 при необходимости можно определить графически траектории характерных точек звеньев, имеющих сложное движение, например, центра тяжести S шатуна AB (рис.14).
4.2. Определение скоростей и ускорений механизма методом планов
Метод планов является одним из самых наглядных. Определению подлежат линейные скорости и ускорения отдельных точек и угловые скорости и ускорения звеньев. При этом предварительно составляются векторные уравнения для скоростей и ускорений точек звеньев, совершающих сложное движение, например:

---

Смотрите также файлы

• Новостная справка за прошедшую неделю о событиях на Донбассе.docx

• Цель занятия закрепление знаний о нормативноправовых основах взаимодействии воспитателя с сотрудниками детского сада, формирование умения применять полученные знания на практике Задание 1.docx

• Guardians of Cloudia.docx

• "политика".docx

• Вавававававававакваапмвпвапвававававававававававаавваваававвааылзщвчсвва.docx