Файл: Оглавление Введение Основные понятия и определения тмм.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 142
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
включает условие отсутствия подреза у колёс с внешним зубчатым венцом и условие отсутствия заедания (интерференции) во внутреннем зацеплении. Эти условия имеют вид:

значение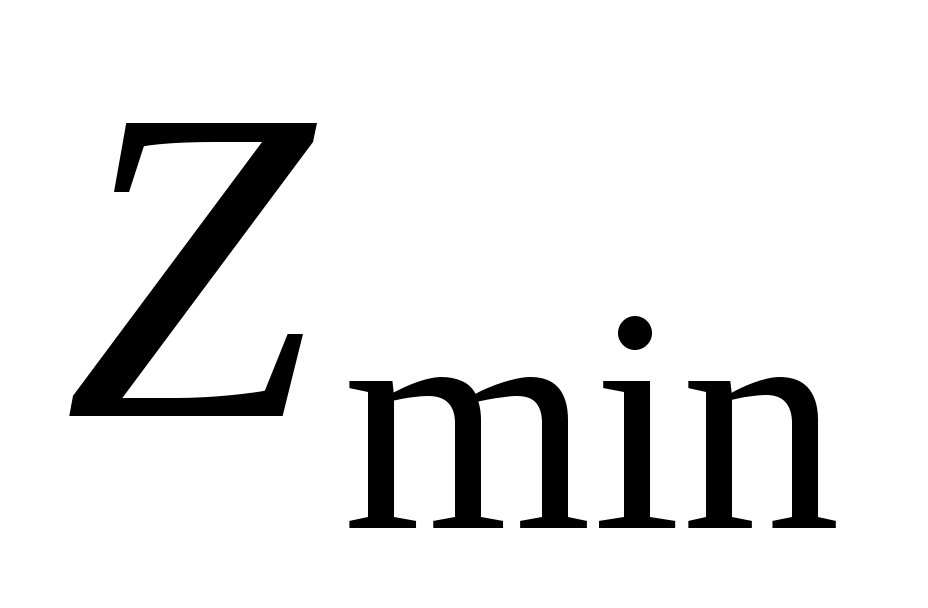 можно принять равным:
можно принять равным:
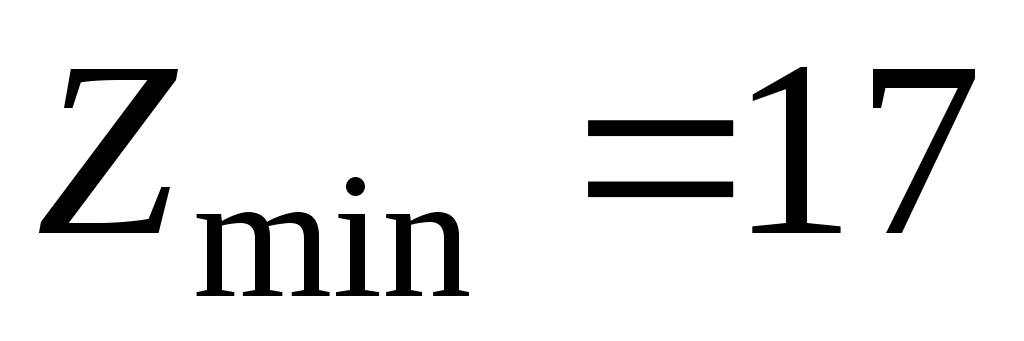 - для колёс с внешним зацеплением;
- для колёс с внешним зацеплением;
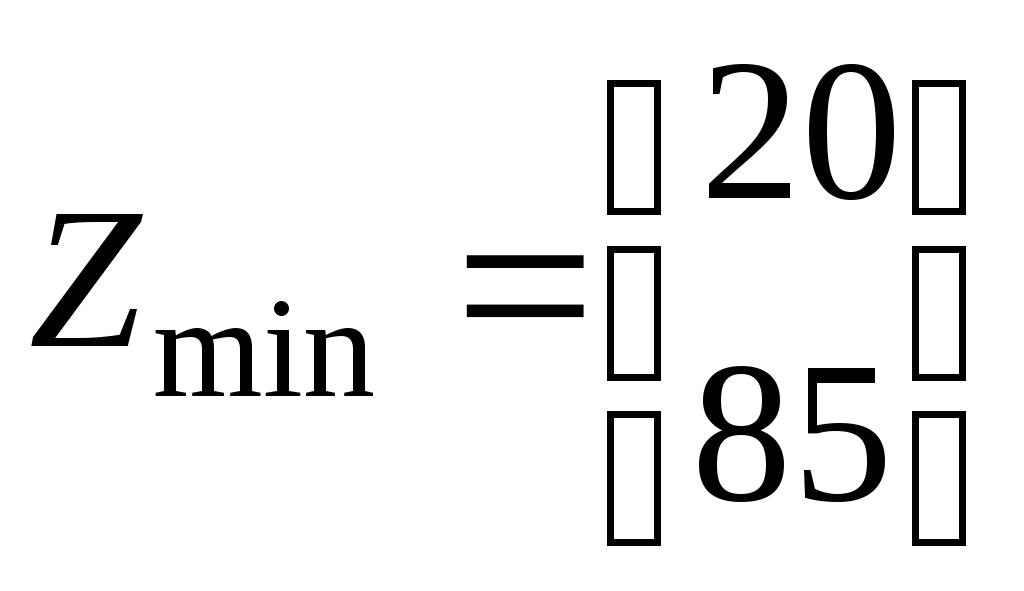 - для колёс с внутренним зацеплением.
- для колёс с внутренним зацеплением.
8.17.2. Методы синтеза эпициклических механизмов
Задача подбора чисел зубьев колёс для эпициклическиого механизма в общей постановке является оптимизационной ввиду множества возможных решений. Её можно считать типичной задачей дискретного нелинейного программирования, если за критерий оптимальности принять габариты или вес механизма, а ограничениями на целочисленные параметры Z1, Z2,… будут условия (а-д). Такую задачу можно решать различными методами, например, численными методами направленного перебора, когда варьируются Z1, Z2,… с целью минимизации габаритов или веса при соблюдении ограничений. Такая задача может быть решена с помощью ЭВМ.
Применяются упрощённые методы, позволяющие найти одно из конструктивно допустимых решений. Один из таких методов – метод сомножителей.
Представим числа зубьев в виде нескольких сомножителей:
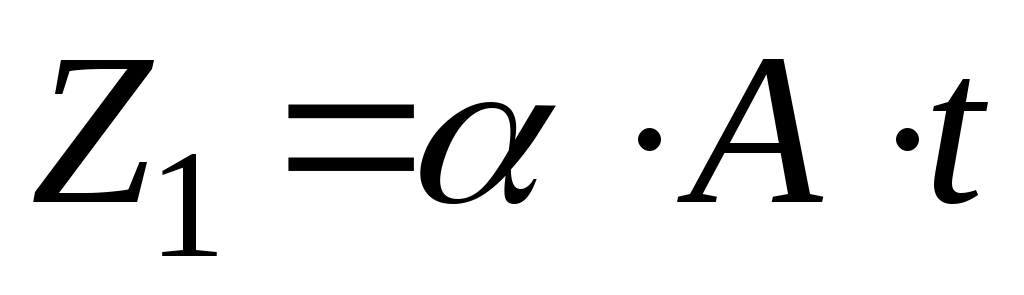 ;
; 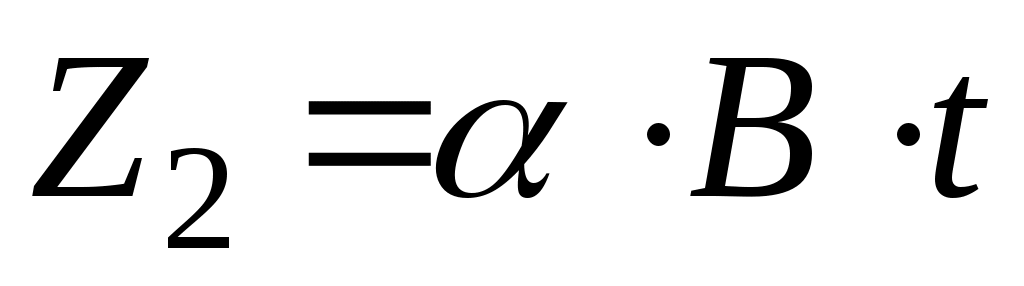 ;
; 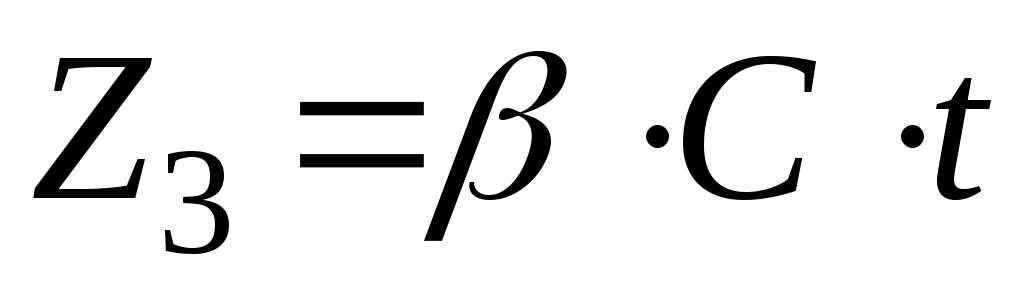 ;
; 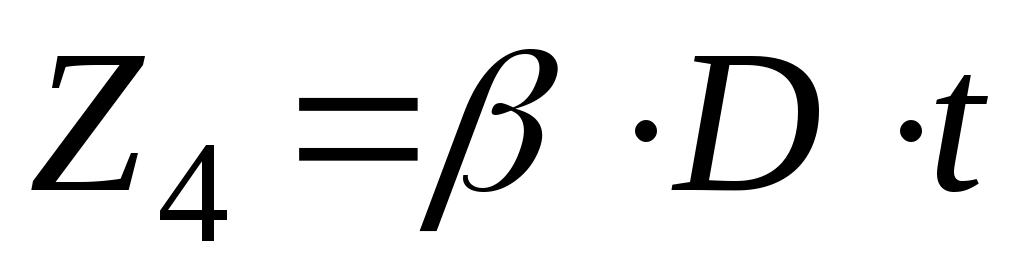 .
.
Из условия (б)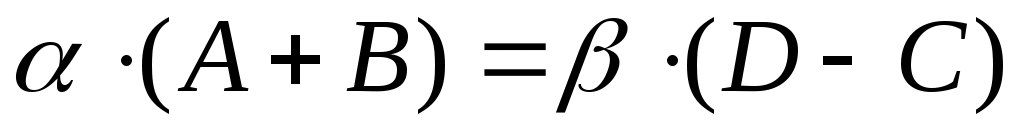 . Это уравнение превращается в тождество при:
. Это уравнение превращается в тождество при: 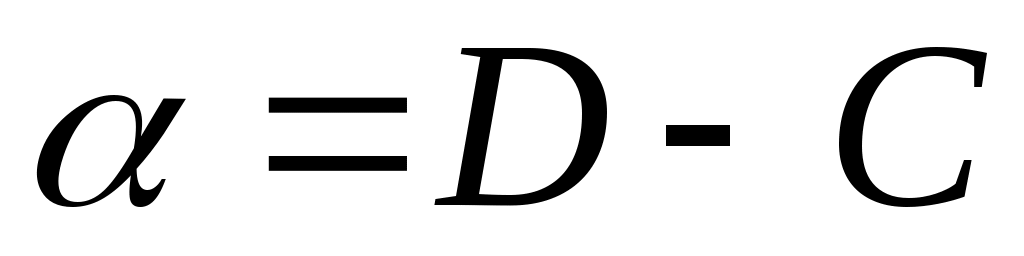 ;
;  .
.
Тогда: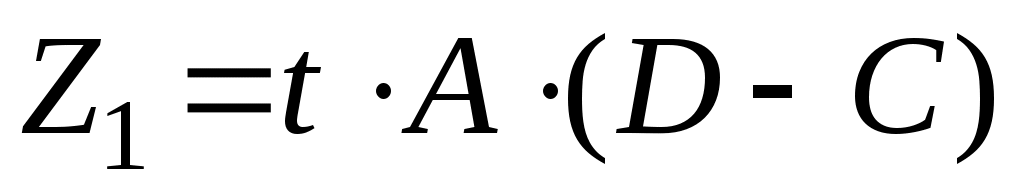 ;
; 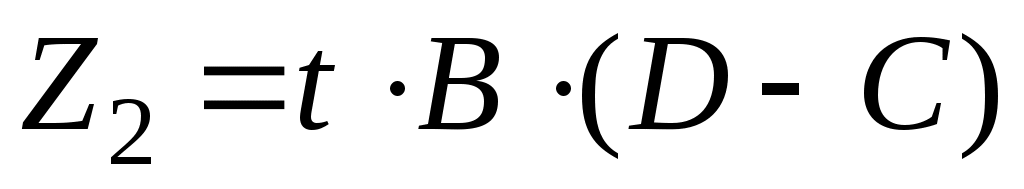 ;
;
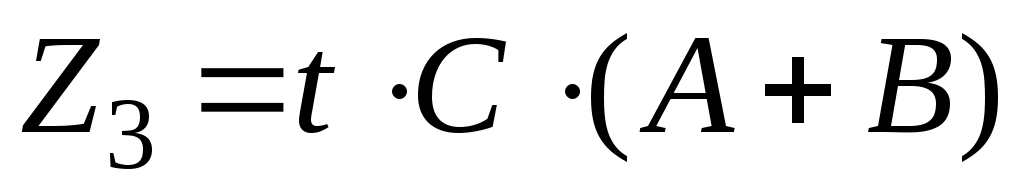 ;
; 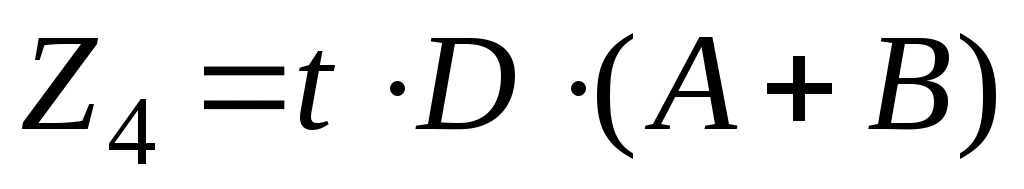 .
.
Подставив эти выражения в условие (а), получим: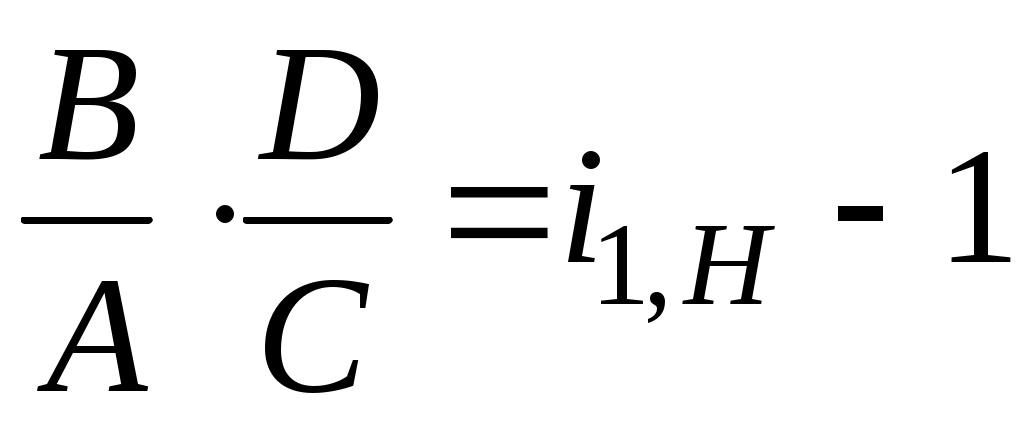 .
.
Таким образом, величину (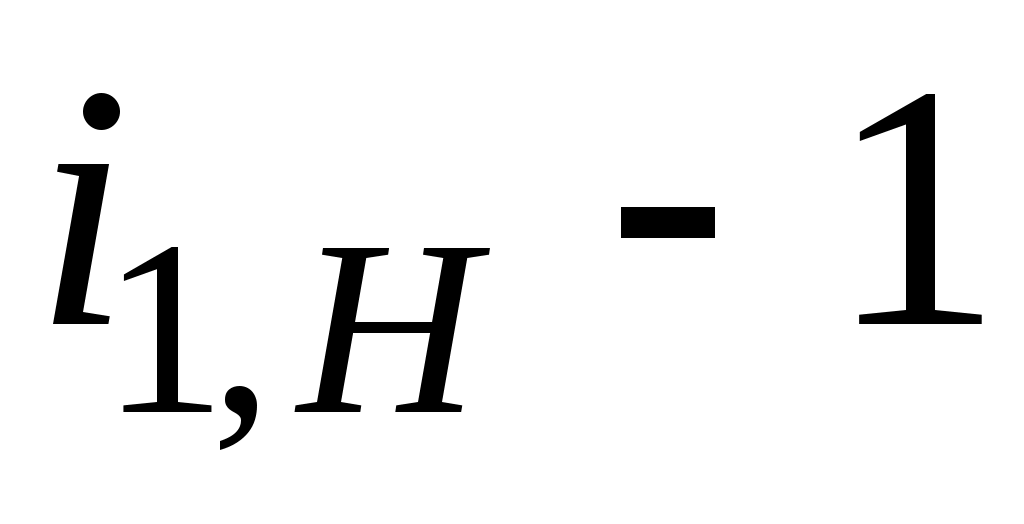 ) можно представить в виде нескольких сомножителей (A, B, C, D). Далее определяются значения t, обеспечивающие выполнение условий сборки и правильного зацепления и выбирается одно из этих значений. Например, из условия сборки (г)
) можно представить в виде нескольких сомножителей (A, B, C, D). Далее определяются значения t, обеспечивающие выполнение условий сборки и правильного зацепления и выбирается одно из этих значений. Например, из условия сборки (г)
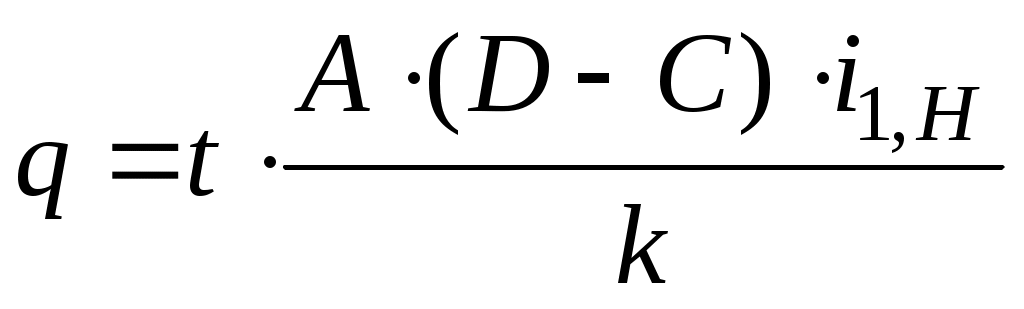
выбираются значения t, обеспечивающие целочисленность q. После этого можно определить числа зубьев.
Пример: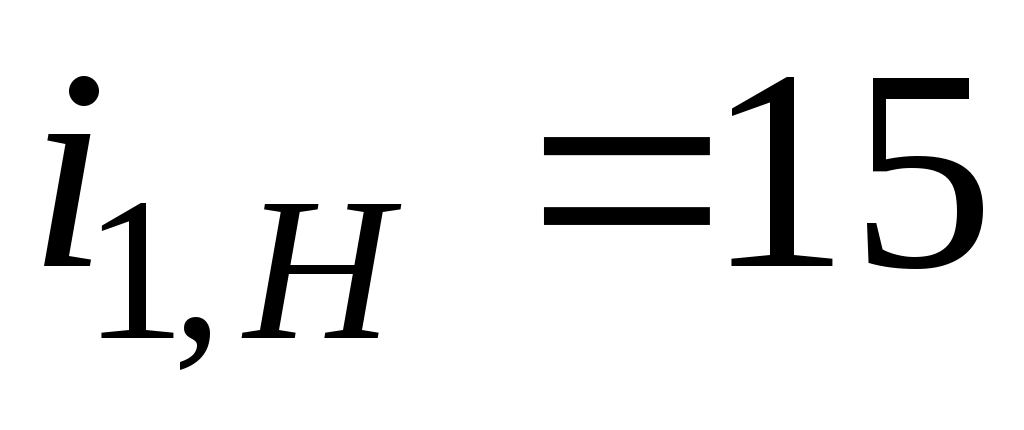 ;
; 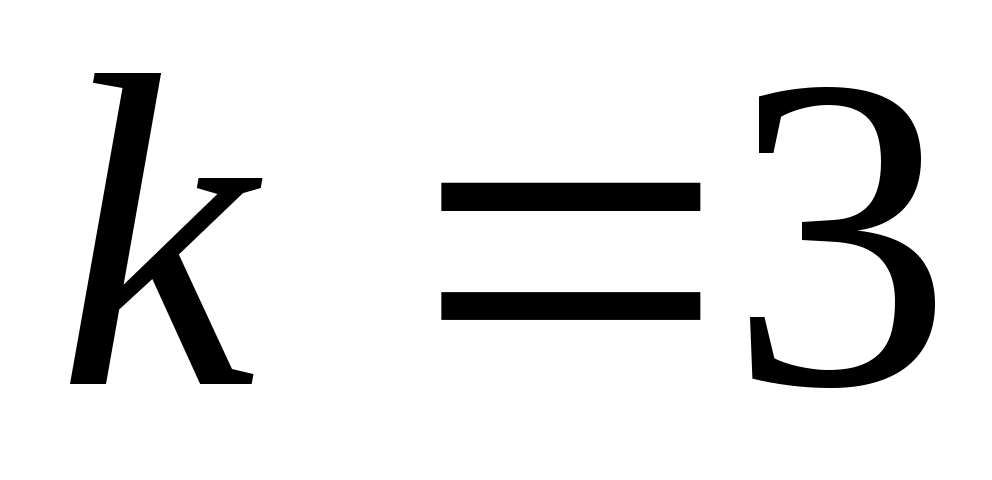 .
.
Представим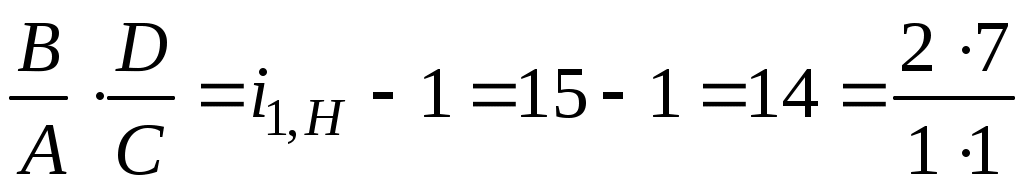 , т.е. А=1; В=2; С=1; D=7. Тогда
, т.е. А=1; В=2; С=1; D=7. Тогда
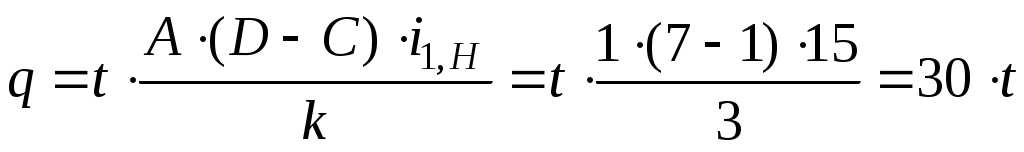 ,
,
следовательно условие сборки выполняется при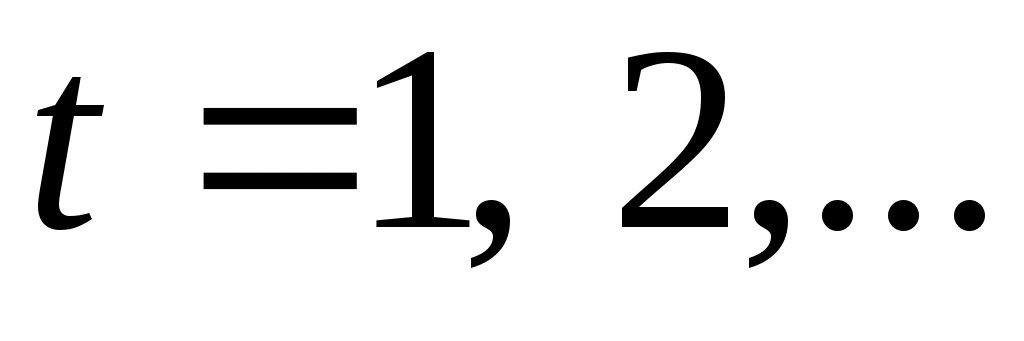 Так как при
Так как при 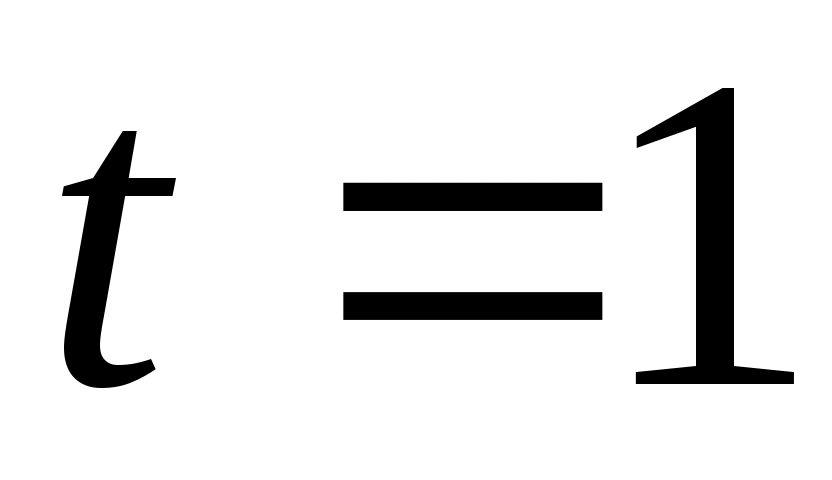 :
:
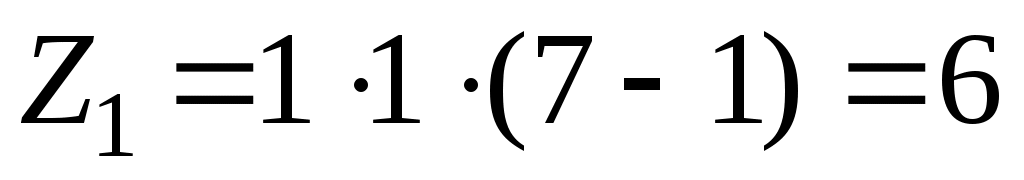 ;
; 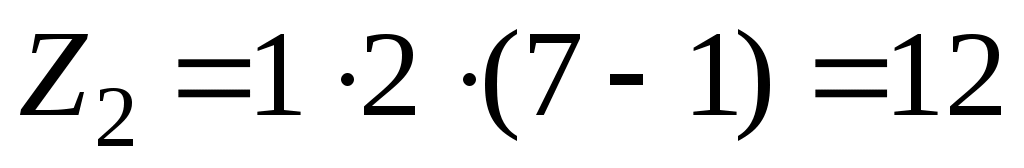 ;
; 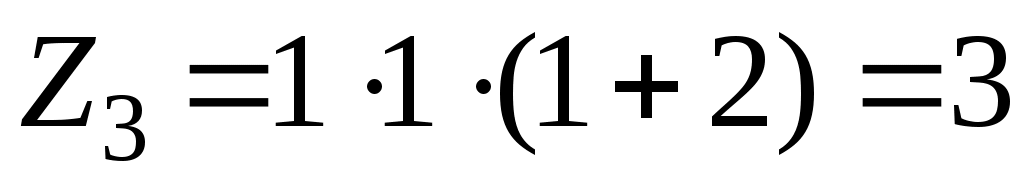 ;
; 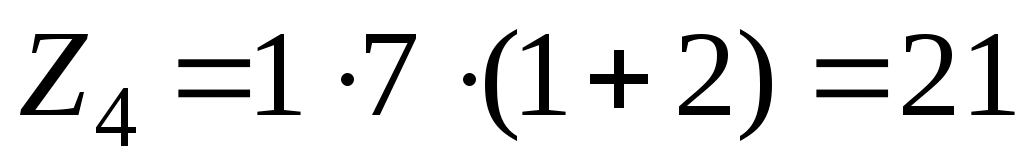 , то с учётом условий правильного зацепления, когда
, то с учётом условий правильного зацепления, когда 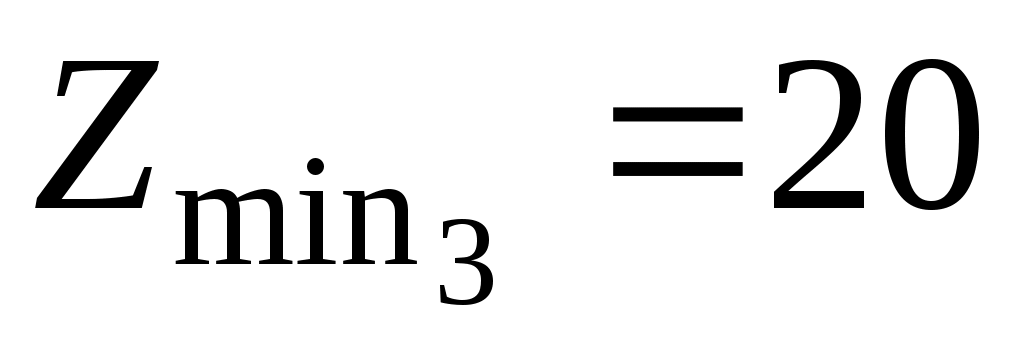 , принимаем
, принимаем 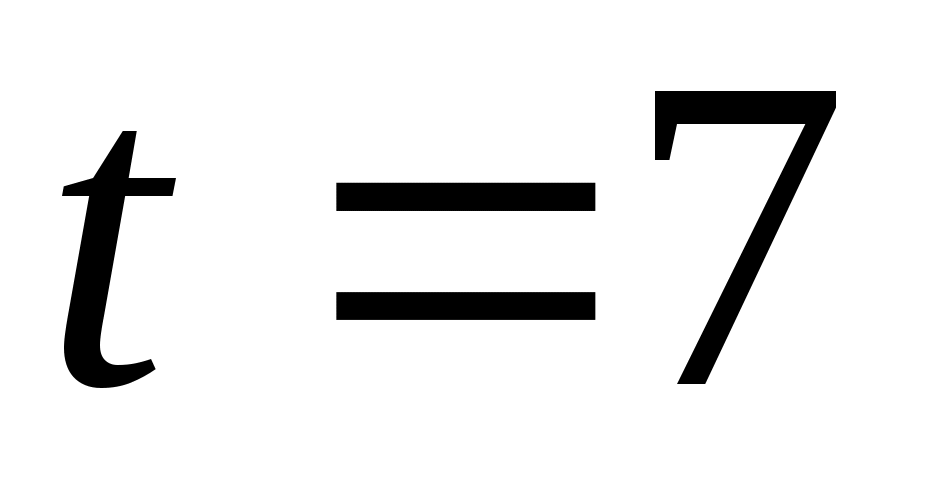 . Тогда
. Тогда 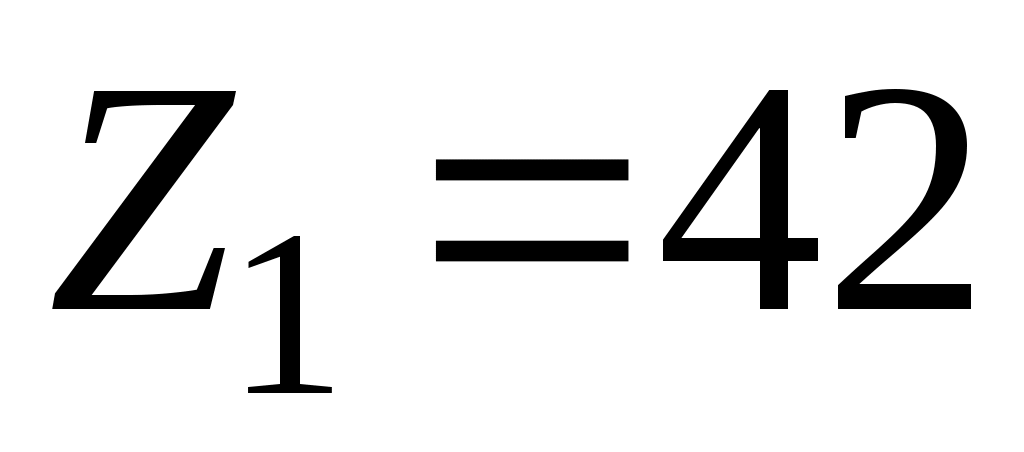 ;
; 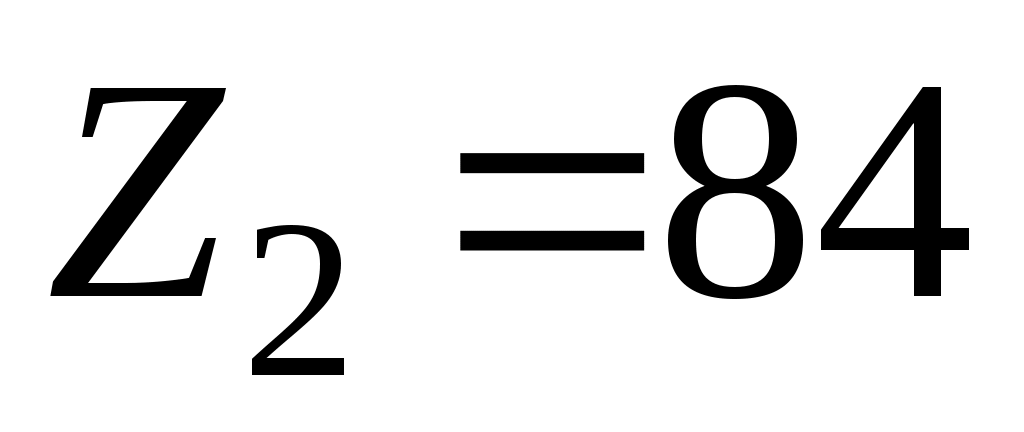 ;
; 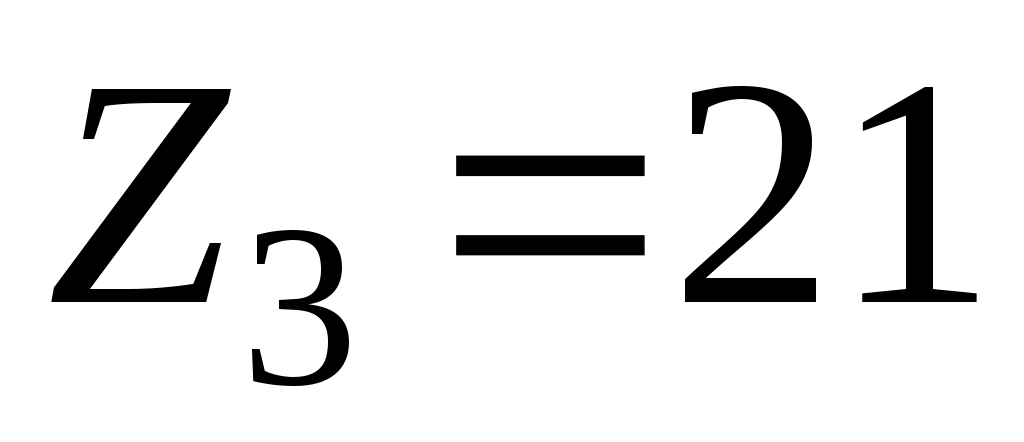 ;
; 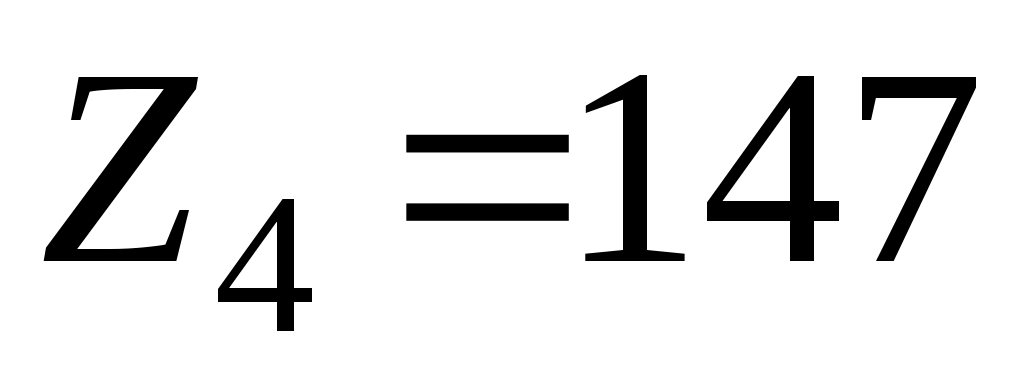 .
.
9. Трение в кинематических парах
9.1. Виды трения
Когда одно тело соприкасается с другим, то независимо от их физического состояния (твёрдое, жидкое, газообразное) возникает явление, называемое трением. В зависимости от характера относительного движения тел различают трение скольжения и трение качения. Сила, препятствующая относительному движению контактирующих тел, называется силой трения. Вектор этой силы лежит в плоскости, касательной к поверхности тел в зоне их контакта.
Сила трения скольжения уменьшается, если соприкасающиеся тела смазаны специальными смазочными материалами, причём, если материал – жидкость, полностью разделяющая контактирующие поверхности, то трение называется жидкостным. При совершенном отсутствии смазки имеет место сухое трение. Если смазывающая жидкость не полностью разделяет трущиеся поверхности, то трение называется полужидкостным или полусухим в зависимости от того, какой из двух видов трения преобладает.
Применяемые смазки делятся на несколько видов: твёрдые, жидкие, газовые; при этом смазка может быть: гидро- или газостатической, когда она поступает под давлением в зазор между трущимися телами, а также гидро- или газодинамической, когда она разделяет трущиеся поверхности в результате давления, самовозникающего в слое жидкости при относительном движении тел.
Сцепление и трение широко используется в современной технике. Благодаря сцеплению движутся различные транспортные средства. Принцип действия фрикционной, ременной и других передач основан на использовании трения. Распространение получила сварка трением. Вместе с тем трение отрицательно сказывается там, где оно вызывает потери энергии
9.2. Трение скольжения в поступательных парах
Сила трения на поверхности соприкосновения двух звеньев направлена в сторону, противоположную скорости относительного движения и приближённо может быть определена по формуле Кулона
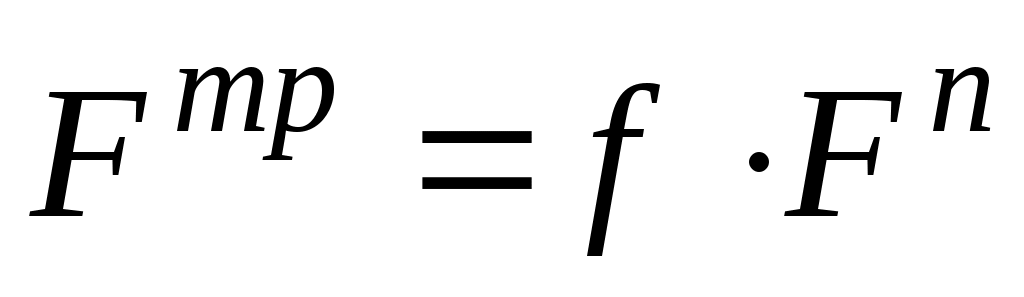 ,
,
где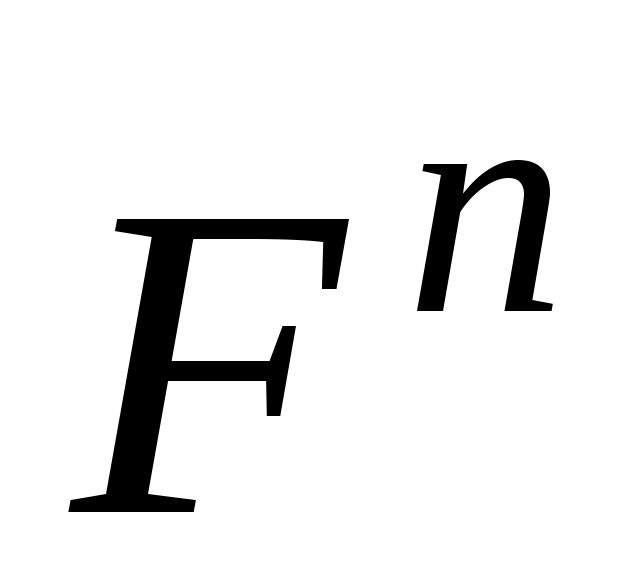
– сила реакции, нормальная к поверхности контакта;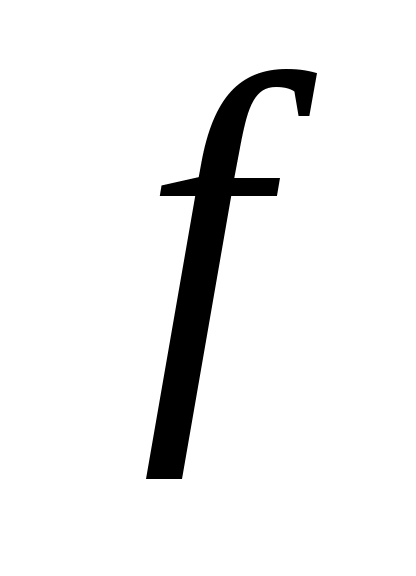 - коэффициент трения скольжения (величина, постоянная в определённом диапазоне скоростей и удельных давлений).
- коэффициент трения скольжения (величина, постоянная в определённом диапазоне скоростей и удельных давлений).
Коэффициент трения зависит от многих факторов (чистоты поверхности, наличия и качества смазки, материала тел и др.) и определяется экспериментально.
Сила трения покоя (сила сцепления), т.е. сила, которую надо преодолеть, чтобы тело привести в движение обычно больше силы трения скольжения, поэтому различают коэффициент сцепления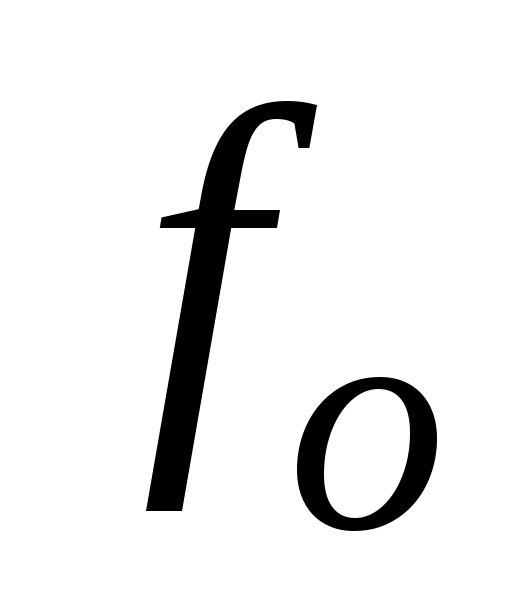 и коэффициент трения скольжения
и коэффициент трения скольжения 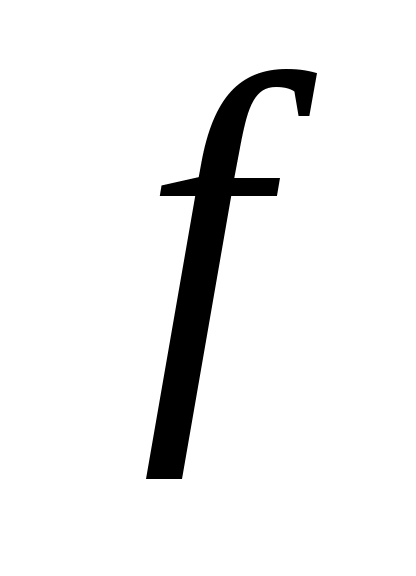 .
.
С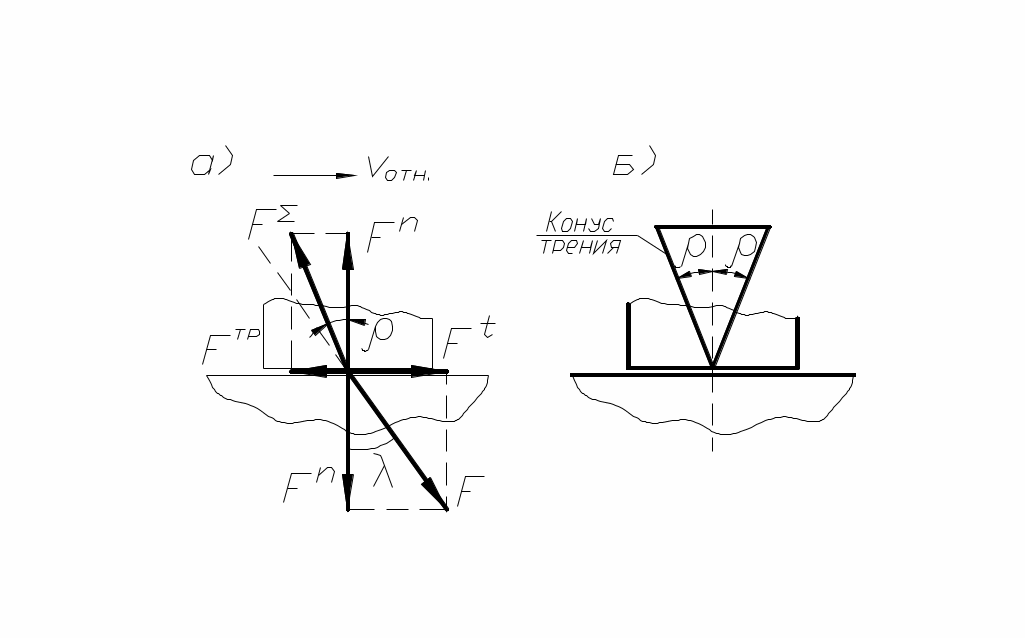 ила трения возникает как результат действия внешних сил F, поэтому она является реактивной силой, в результате действия которой суммарная реакция
ила трения возникает как результат действия внешних сил F, поэтому она является реактивной силой, в результате действия которой суммарная реакция 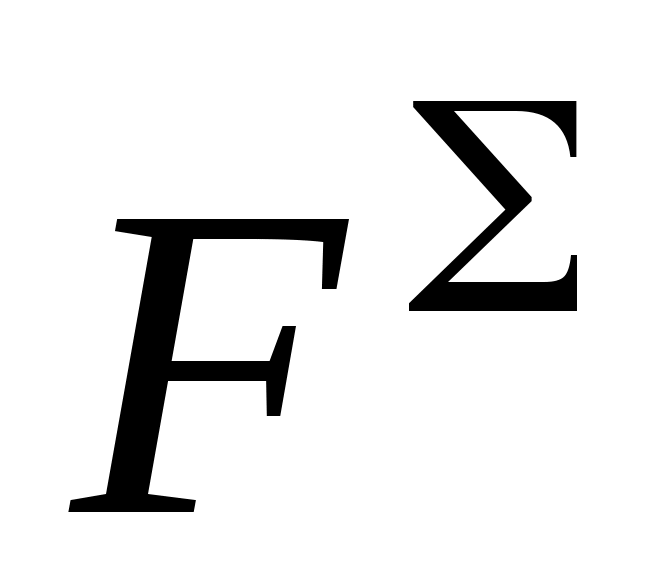 отклоняется на угол
отклоняется на угол 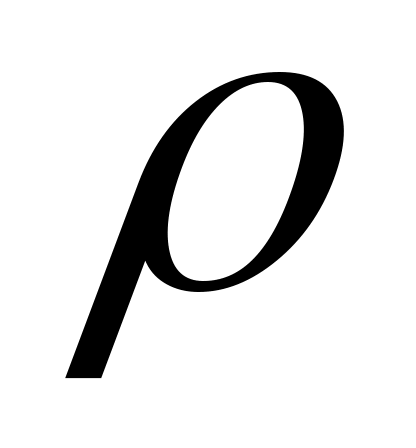 от нормали к трущимся поверхностям (рис. 92, а). При этом
от нормали к трущимся поверхностям (рис. 92, а). При этом 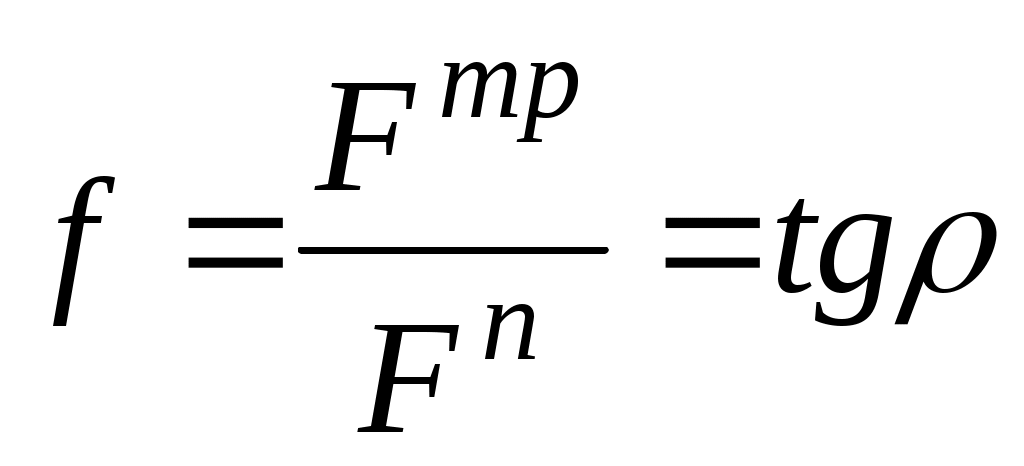 . Угол
. Угол 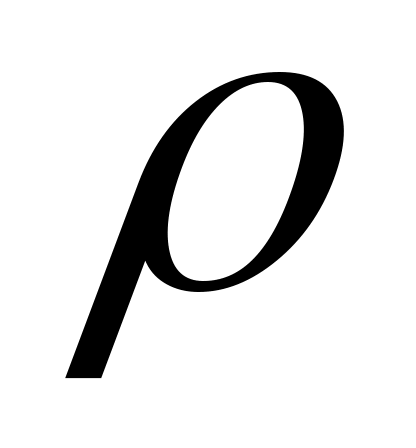 называется углом трения скольжения.
называется углом трения скольжения.
Если построить конус с углом при вершине 2·ρ (рис. 92, б), то получим конус трения. Движение возможно при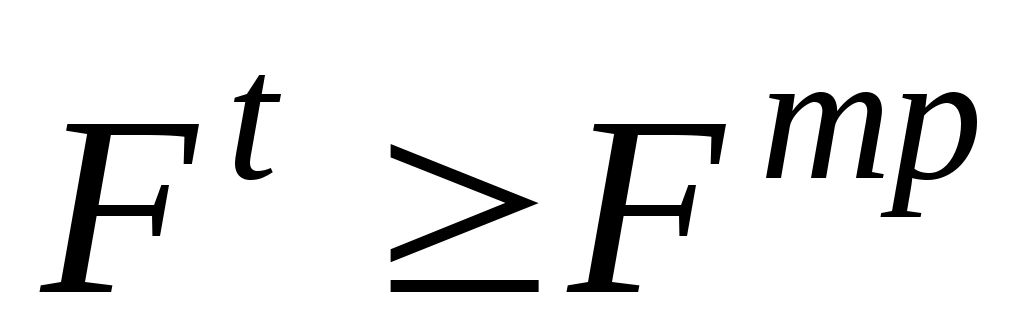 или при
или при
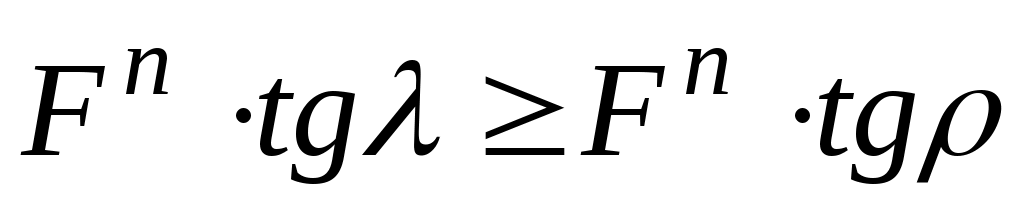 ,
,
т.е. при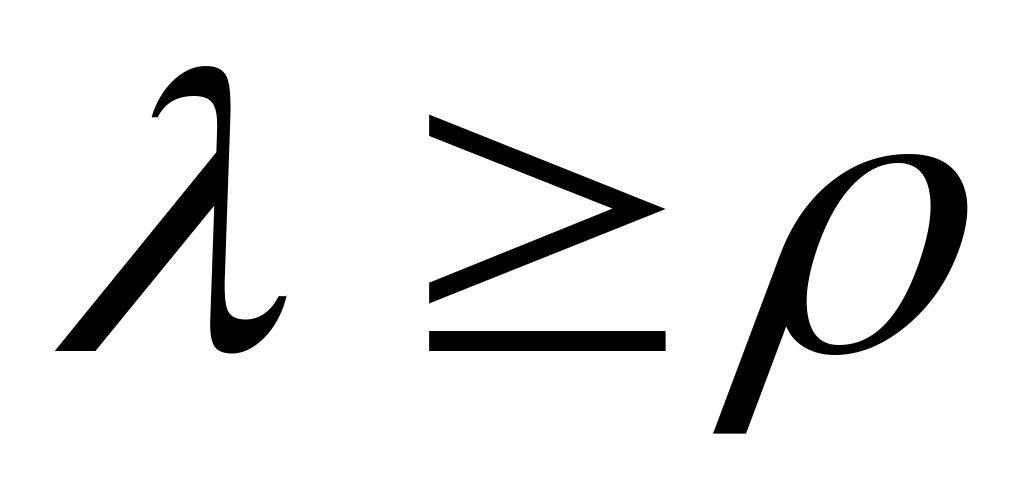 , причём, если
, причём, если 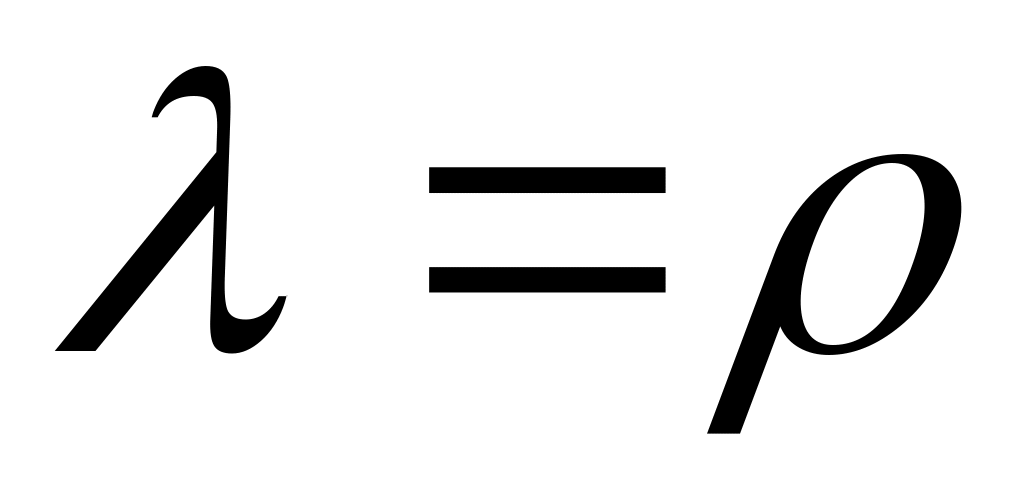 , то движение происходит с
, то движение происходит с 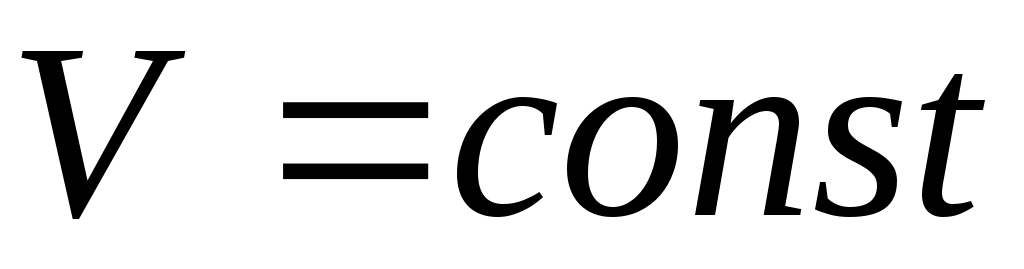 .
.
рис. 92
В общем случае движение возможно, если сила внешнего воздействия F находится за пределами конуса трения.
Мощность, затрачиваемая на трение скольжения равна:
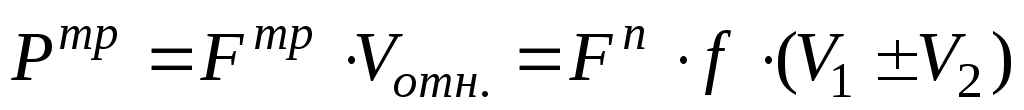 ,
,
где знак зависит от направления скоростей.
9.3. Трение скольжения во вращательных парах
Вращательные кинематические пары, образуемые цапфами валов и их опорами, широко распространены в машиностроении. Цапфами называются части валов и осей, посредством которых они опираются на подшипники. Трение цапф в подшипниках удобно оценивать величиной момента сил трения скольжения относительно оси вращения (рис. 93):
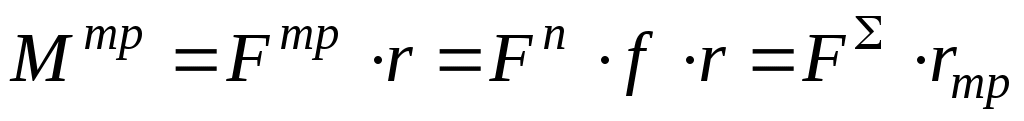
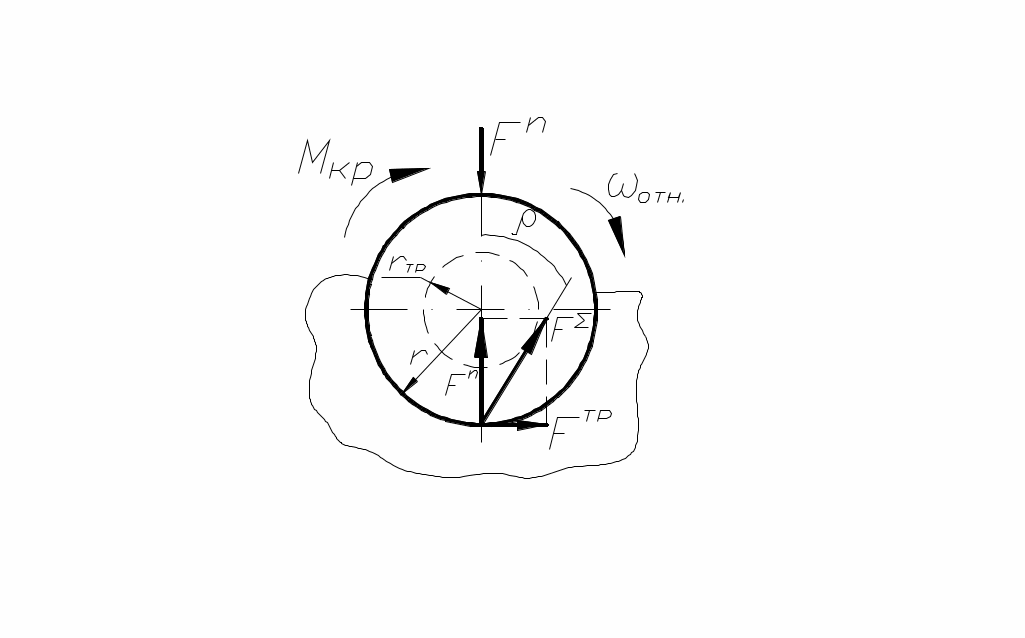 ,
,
где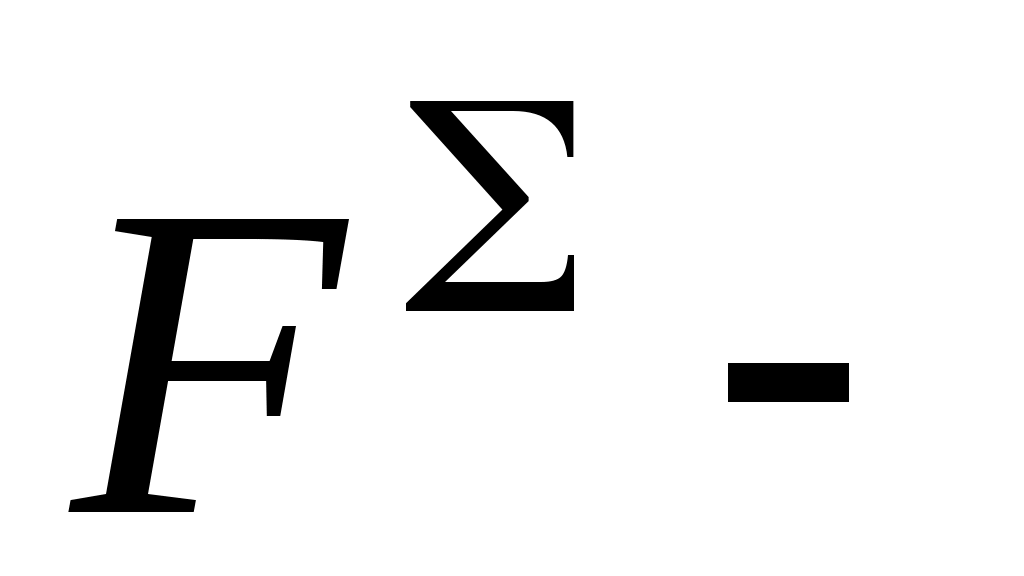 полная реакция;
полная реакция;
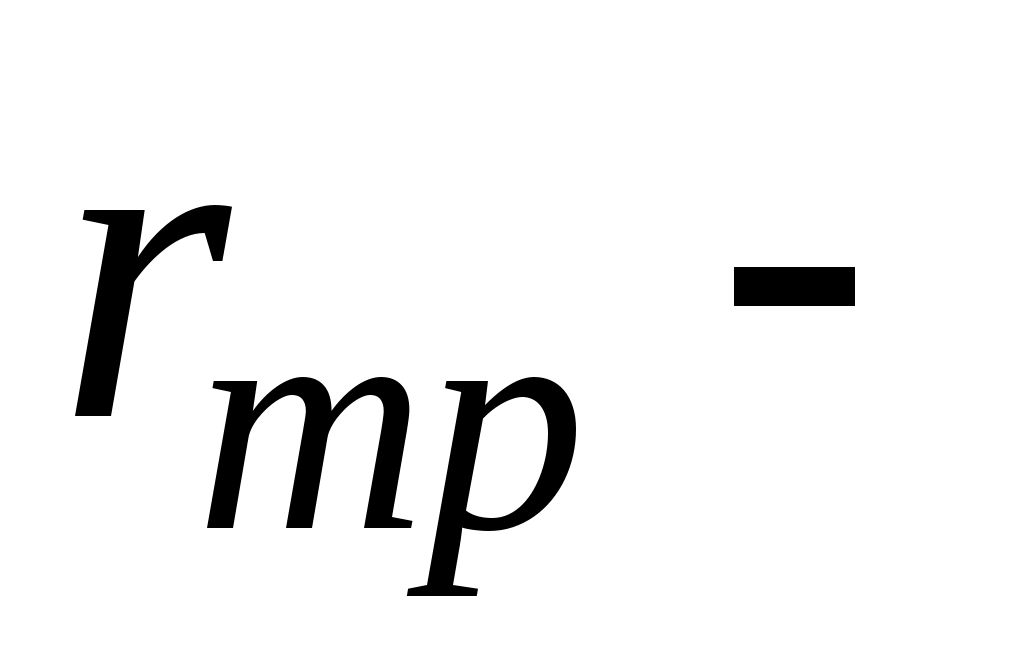 радиус круга трения, равный:
радиус круга трения, равный:
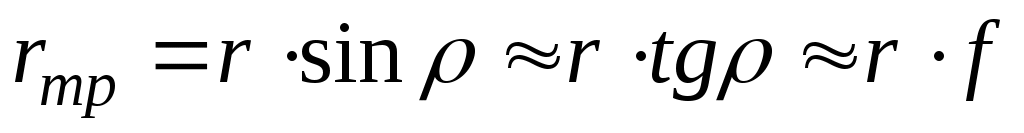 .
.
Мощность, затрачиваемая на трение, равна:
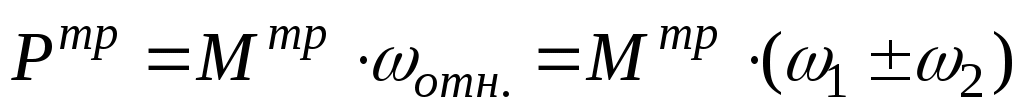 .
.
рис. 93
9.4. Трение качения
В случаях идеально твёрдых тел, одно из которых катится по поверхности другого, соприкосновение их происходит по линии или в точке и сопротивление качению отсутствует, так как линии действия сил совпадают (рис. 94, а) и сумма моментов относительно точки А равна
совпадают (рис. 94, а) и сумма моментов относительно точки А равна 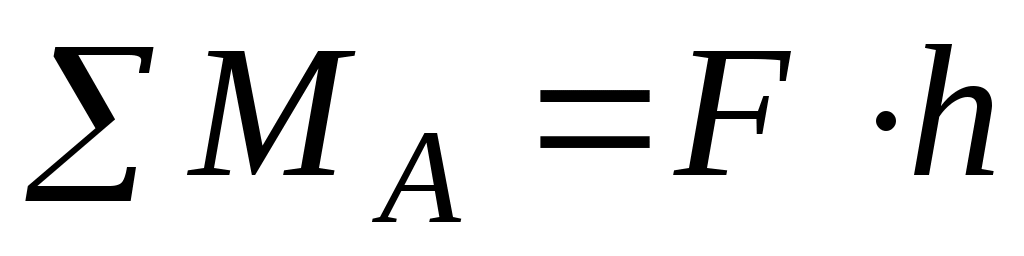 . В действительности соприкосновение происходит не по линии, а по поверхности вследствие деформаций (рис. 94, б) и сумма моментов (
. В действительности соприкосновение происходит не по линии, а по поверхности вследствие деформаций (рис. 94, б) и сумма моментов (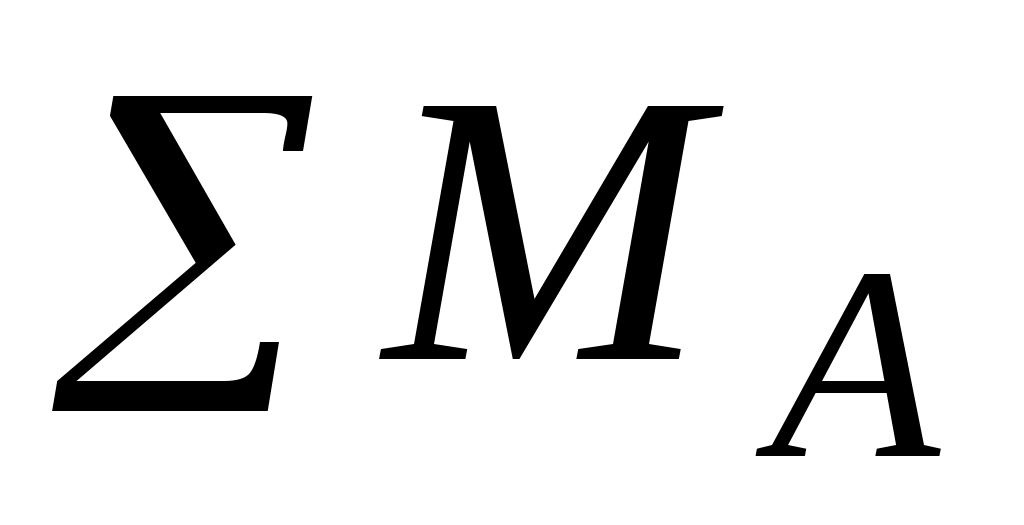 ) равна:
) равна:
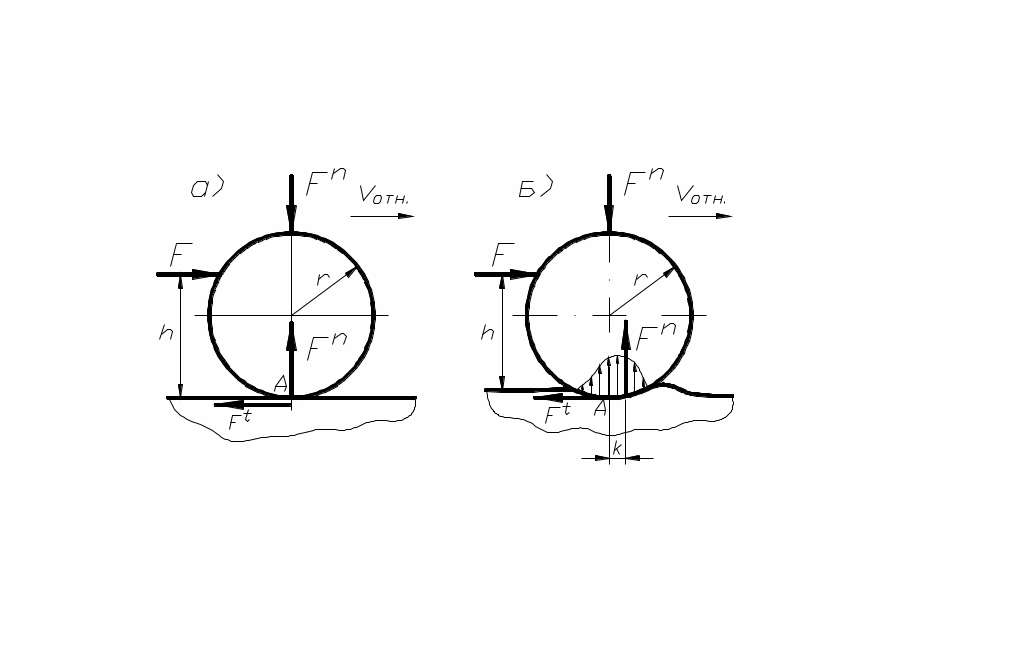
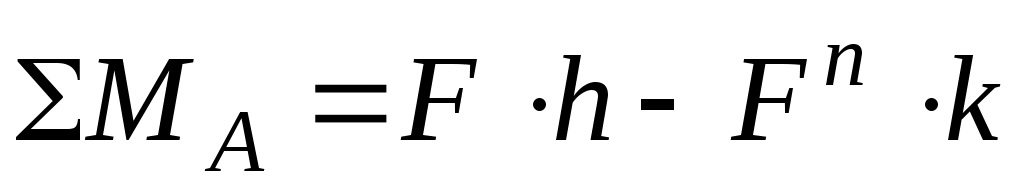 .
.
При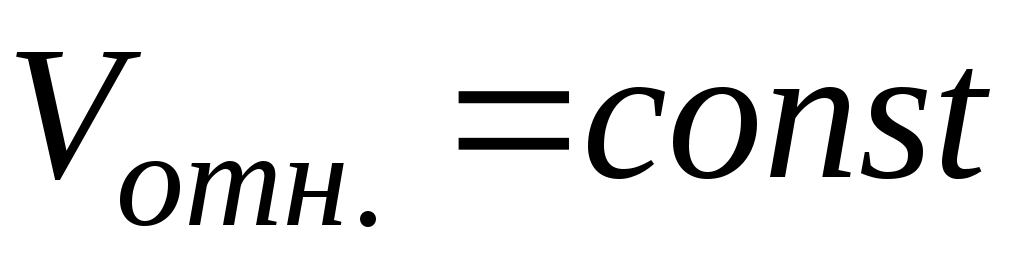 и
и 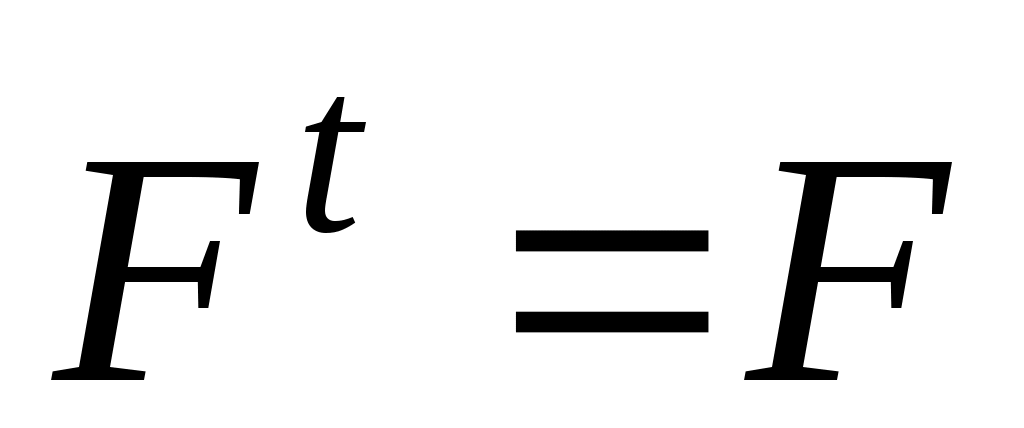 получим
получим 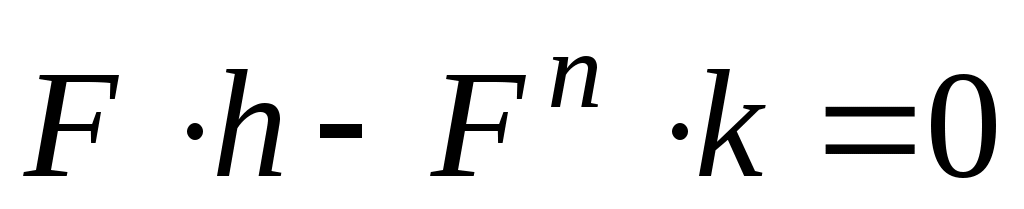 , т.е.
, т.е.
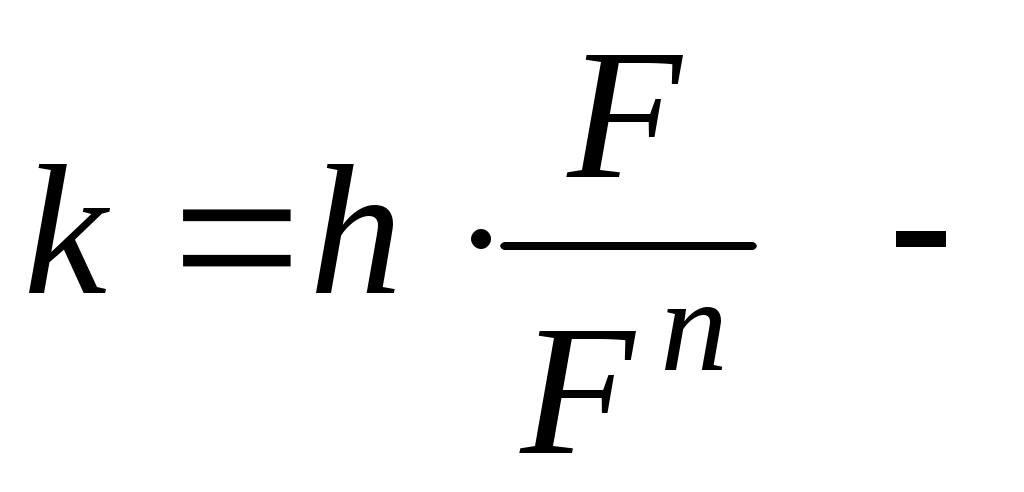
значение
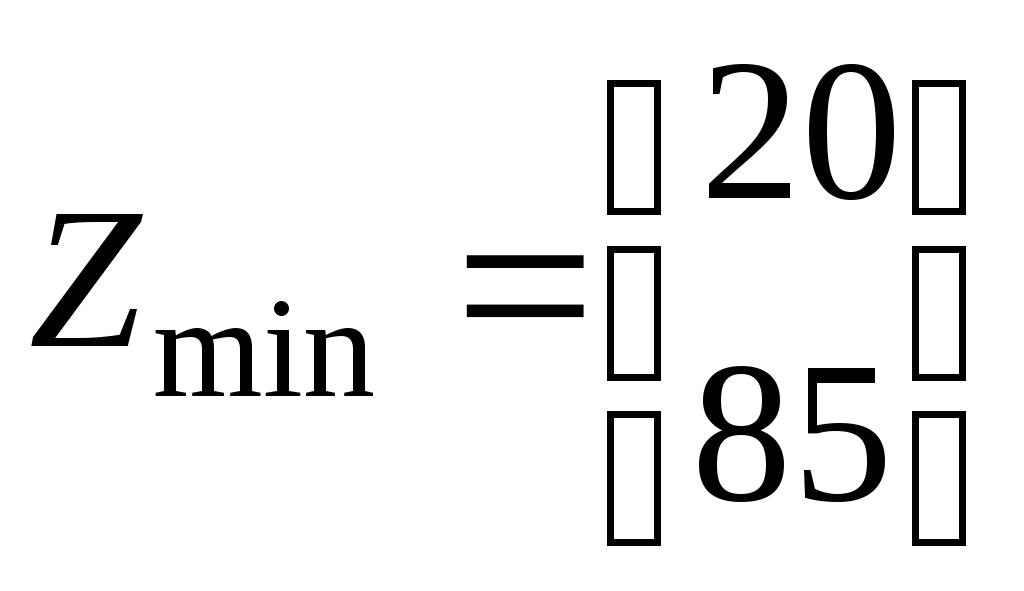 - для колёс с внутренним зацеплением.
- для колёс с внутренним зацеплением.8.17.2. Методы синтеза эпициклических механизмов
Задача подбора чисел зубьев колёс для эпициклическиого механизма в общей постановке является оптимизационной ввиду множества возможных решений. Её можно считать типичной задачей дискретного нелинейного программирования, если за критерий оптимальности принять габариты или вес механизма, а ограничениями на целочисленные параметры Z1, Z2,… будут условия (а-д). Такую задачу можно решать различными методами, например, численными методами направленного перебора, когда варьируются Z1, Z2,… с целью минимизации габаритов или веса при соблюдении ограничений. Такая задача может быть решена с помощью ЭВМ.
Применяются упрощённые методы, позволяющие найти одно из конструктивно допустимых решений. Один из таких методов – метод сомножителей.
Представим числа зубьев в виде нескольких сомножителей:
Из условия (б)
Тогда:
Подставив эти выражения в условие (а), получим:
Таким образом, величину (
выбираются значения t, обеспечивающие целочисленность q. После этого можно определить числа зубьев.
Пример:
Представим
следовательно условие сборки выполняется при
9. Трение в кинематических парах
9.1. Виды трения
Когда одно тело соприкасается с другим, то независимо от их физического состояния (твёрдое, жидкое, газообразное) возникает явление, называемое трением. В зависимости от характера относительного движения тел различают трение скольжения и трение качения. Сила, препятствующая относительному движению контактирующих тел, называется силой трения. Вектор этой силы лежит в плоскости, касательной к поверхности тел в зоне их контакта.
Сила трения скольжения уменьшается, если соприкасающиеся тела смазаны специальными смазочными материалами, причём, если материал – жидкость, полностью разделяющая контактирующие поверхности, то трение называется жидкостным. При совершенном отсутствии смазки имеет место сухое трение. Если смазывающая жидкость не полностью разделяет трущиеся поверхности, то трение называется полужидкостным или полусухим в зависимости от того, какой из двух видов трения преобладает.
Применяемые смазки делятся на несколько видов: твёрдые, жидкие, газовые; при этом смазка может быть: гидро- или газостатической, когда она поступает под давлением в зазор между трущимися телами, а также гидро- или газодинамической, когда она разделяет трущиеся поверхности в результате давления, самовозникающего в слое жидкости при относительном движении тел.
Сцепление и трение широко используется в современной технике. Благодаря сцеплению движутся различные транспортные средства. Принцип действия фрикционной, ременной и других передач основан на использовании трения. Распространение получила сварка трением. Вместе с тем трение отрицательно сказывается там, где оно вызывает потери энергии
9.2. Трение скольжения в поступательных парах
Сила трения на поверхности соприкосновения двух звеньев направлена в сторону, противоположную скорости относительного движения и приближённо может быть определена по формуле Кулона
где
– сила реакции, нормальная к поверхности контакта;
Коэффициент трения зависит от многих факторов (чистоты поверхности, наличия и качества смазки, материала тел и др.) и определяется экспериментально.
Сила трения покоя (сила сцепления), т.е. сила, которую надо преодолеть, чтобы тело привести в движение обычно больше силы трения скольжения, поэтому различают коэффициент сцепления
С
 ила трения возникает как результат действия внешних сил F, поэтому она является реактивной силой, в результате действия которой суммарная реакция
ила трения возникает как результат действия внешних сил F, поэтому она является реактивной силой, в результате действия которой суммарная реакция Если построить конус с углом при вершине 2·ρ (рис. 92, б), то получим конус трения. Движение возможно при
т.е. при
рис. 92
В общем случае движение возможно, если сила внешнего воздействия F находится за пределами конуса трения.
Мощность, затрачиваемая на трение скольжения равна:
где знак зависит от направления скоростей.
9.3. Трение скольжения во вращательных парах
Вращательные кинематические пары, образуемые цапфами валов и их опорами, широко распространены в машиностроении. Цапфами называются части валов и осей, посредством которых они опираются на подшипники. Трение цапф в подшипниках удобно оценивать величиной момента сил трения скольжения относительно оси вращения (рис. 93):
 ,
, где
Мощность, затрачиваемая на трение, равна:
рис. 93
9.4. Трение качения
В случаях идеально твёрдых тел, одно из которых катится по поверхности другого, соприкосновение их происходит по линии или в точке и сопротивление качению отсутствует, так как линии действия сил

При