ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 256
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
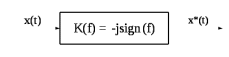
Рис.10.4 – Преобразователь Гильберта для сигнала общего вида, где sign(f) сигнальная функция, равная 1, если f > 0 и -1, если f < 0.
Так как вещественная часть и мнимая сопряжены по Гильберту, то огибающая и фаза сигнала определяется однозначно:
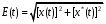
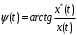
Для узкополосного процесса справедливо представление рядом Фурье, если мнимая часть, получена с помощью преобразователя Гильберта, показанного на рисунке 10.4:
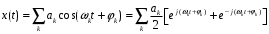
то сопряженный ему ряд:
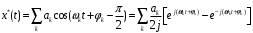
Таким образом, простейшему сигналу в виде гармонического колебания
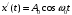соответствует аналитический сигнал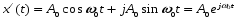
10.2 Огибающая и фаза узкополосного гауссовского случайного процесса и суммы гармонического сигнала и узкополосного гауссовского случайного сигнала
10.2.1 Огибающая и фаза узкополосного гауссовского случайного процесса.
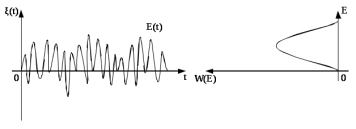
Рис.10.4 - Временная и вероятностная характеристика огибающей СП
Если процесс стационарный, то каждую реализацию ξi(t) можно разложить на квадратурные составляющие:
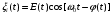
или
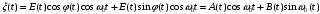
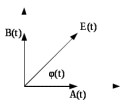
Рис.10.5 - Разложение огибающей СП на квадратурные составляющие
Поскольку ξ(t) – нормальный (гауссовский) процесс, то W(ξ), W(A) и W(B) имеют нормальное распределение:
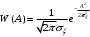
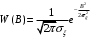
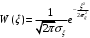
а их функция некоррелированные
в совпадающие моменты времени 
.
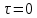
Найдем плотность вероятности огибающей
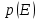и фазы
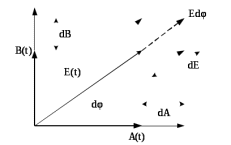
Рис.10.6 - Переход к полярной системе координат
В прямоугольных координатах (рис. 10.6) вероятность того, что случайная величина E будет находиться в пределах прямоугольника, ограниченного сторонами (A, A+dA) и (B, B+dB) можно выразить через совместную плотность вероятности:
P = W2 (A, B)dAdB
Вероятность этого же события можно записать в полярных координата E и φ
P = W2(E,φ)dEdφ
следовательно:
W2(A, B)dAdB = W2(E, φ)dEdφ (10.2)
Поскольку речь идет об одной и той же вероятности, то площадь элементарного прямоугольника dAdB должна быть равной элементарной площади в полярных координатах:
dAdB =EdEdφ(10.3)
Кроме того, вследствие статической независимости квадратурных составляющих, а также их W(A) и W(B) с учетом (10.2):
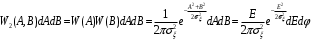(10.4)Сопоставляя (10.2) и (10.3), можно получить:
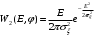(10.5)Выражение (10.4) определяет совместную плотность вероятности огибающей E и фазы φ. Для определения плотности вероятности огибающей проинтегрируем (10.4) по всем возможным значениям
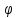в пределах от 0 до 2π:
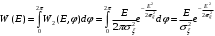(10.6)Для определения плотности вероятности фазы P(φ) надо совместную плотность (10.4) проинтегрировать по всем возможным значениям огибающей:
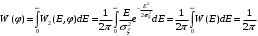(10.7)Из (10.7) видно, что плотность вероятности фазы равномерна по всей области возможных значений φ от -π до +π
(рисунок 10.7). 
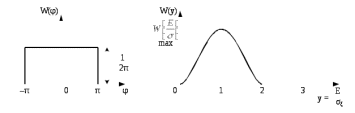
Рис. 10.7 - ФПВ огибающей и фазы СП при нулевой средней
Выражение (10.6) может быть безразмерным, если обозначить y = E/σξ
При переходе от E к y должно выполняться равенство:
W(E)dE = W(y
)dy (10.7)
Подставляя в (10.7) значение
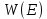из (10.5) и учитывая dE = σξdy получим:
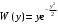(10.8)Плотность вероятности, определяемая (12.8), называется распределением Рэлея.
Здесь переменная
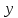может принимать лишь неотрицательные значения, в отличии от нормального распределения, где 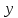может принимать и положительные, и отрицательные значения. Из рисунка 10.7 видно, что максимальное значение плотности вероятности огибающей имеет место при y = 1 или, что то же самое, e = σξ.Кроме того, в рассматриваемом процессе ξ(t) нет постоянной составляющей, среднее значение огибающей не равно 0.
10.2.2 Огибающая и фаза суммы гармонического колебания и
узкополосного гауссовского случайного сигнала.
Задача решается аналогично. Пусть имеется сумма узкополосного нормального стационарного процесса и ξi= E(t)cos(ω0t – φ) и гармонического сигнала
S(t) = U0 (t) cosω0t.
В этом случае:
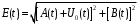(10.9)
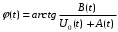(10.9)Аналогично находятся W2 (E, φ), W(E) и W(φ)
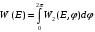
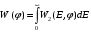
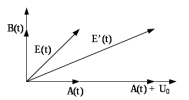
Рис.10.8 - Огибающая случайного процесса при нулевой и ненулевой средней
Если найти совместную плотность вероятности огибающей и фазы и проинтегрировать по фазе в пределах от -π до +π
то придем к распределению Райса (или обобщенно Рэлея) для плотности вероятности огибающей суммы сигнала и шума: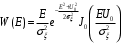
(10.11)J0 – модифицированная функция Бесселя нулевого порядка:
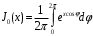
На рисунке 10.9 приведена зависимость модифицированной функции Бесселя нулевого порядка от аргумента х.
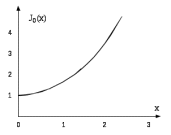
Рис.10.9 – Зависимость модифицированной функции Бесселя нулевого порядка от аргумента
При U0 = 0, J0 = 1 - получим распределение Рэлея как частный случай.
При U0/σξ >> 1- распределение стремится к нормальному (с ненулевым средним).
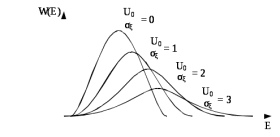
Рис.10.10 – Функция плотности вероятностей огибающей при различных U0/σξ
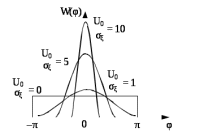
Рис.10.11 – Функция плотности вероятностей фазы при различных U0/σξ
Чем больше амплитуда сигнала
, тем ближе фаза результирующего колебания к фазе этого сигнала.
10.3 Контрольные вопросы и задачи.
10.3.1 В каком случае справедливо преобразование Гильберта?
10.3.2 Перечислить основные свойства аналитического сигнала.
10.3.3 Показать на примере, что в спектре аналитического сигнала присутствует только положительные частоты.
10.3.4 Доказать, что скалярное произведение действительного и сопряженного сигнала равно нулю.
10.3.5 Доказать, что при общем фазовом сдвиге всех частотных компонент сигнала X(t) на угол θ, аналитический сигнал умножается на exp( jθ ), а транспонирование спектра умножается на exp( jΔωt ).
10.3.6 Показать, что огибающую аналитического сигнала
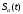можно находить по формуле: 
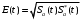, где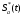 
-функция, комплексно сопряженная к функции 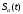.10.3.7 Сигнал многоканальной системы связи представлен в виде:
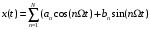
Записать этот сигнал в виде огибающей и фазы:
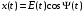
10.3.8 Дана гармоническая помеха:
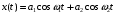
представить её в виде:
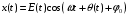
Сначала для частоты
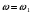, затем для частоты 
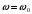, где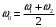 
Решение провести двумя способами. По первому способу получить решение, не прибегая к понятию аналитического сигнала, то есть выполняя известные операции сложения гармонических колебания; по второму – с использованием понятия аналитического сигнала.
10.3.9 Дан сигнал
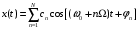, являющимся типичным примером сигнала в многоканальных системах связи. Получить выражение аналитического сигнала в общем виде, а затем для частного случая 
, 
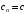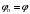. Линейный член выделить по отношению к средней частоте