8.3 Контрольные вопросы и задачи

8.3.1 Почему спектральная плотность случайного сигнала, определенная по одной реализации, не характеризует весь ансамбль сигналов.

8.3.2 Дать определение теоремы Винера-Хинчина и пояснить на примере связь спектральной плотности мощности с функцией корреляции случайного процесса.

8.3.3 Показать, что значение спектральной плотности мощности на нулевой частоте равно интегралу корреляционной функции.

8.3.4 Почему корреляционная функция случайного процесса не может иметь прямоугольный характер?

8.3.5 Определить спектральную плотность мощности случайного процесса, типа телеграфного сигнала, имеющего функцию корреляцию вида 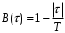, только для τ ≤ Т и B(τ) = 0 для τ > T.

8.3.6 Почему интервал корреляции служит для оценки скорости изменения реализаций случайного процесса?

8.3.7 Определить функцию корреляции и интервал корреляции случайного процесса, имеющего спектральную плотность мощности вида .

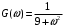8.3.8 Определить интервал корреляции широкополосного случайного сигнала, имеющего равномерный спектр, ограниченного верхней частотой равной 10 МГц.

8.3.9 Определить среднюю мощность узкополосного случайного процесса, имеющую ширину полосы сигнала, равную 100 МГц и спектральную плотность N = 1 mВт/Гц.

8.3.10 Определить интервал корреляции узкополосного случайного процесса с центральной частотой, равной 20 МГц и с шириной полосы, равной 100кГц.

9 Прохождение случайных сигналов через радиотехнические цепи

9. Преобразование случайных сигналов в линейных инерционных

радиотехнических цепях

Из всего разнообразия линейных радиотехнических цепей остановимся на цепях с сосредоточенными параметрами. Линейную инерционную цепь охарактеризуем только коэффициентом передачи для простоты рассмотрения, как показано на рисунке 9.1.

---

Рис.9.1. Линейная инерционная цепь

Задачи, которые решаются при прохождения случайных сигналов через линейные инерционные цепи - это нахождение числовых характеристик сигнала y(t) на выходе цепи, а именно: матожидания m_y, дисперсии σ_y², cпектральной плотности мощности G_y(ω), эффективной полосы частот Δω_yэфф, функции корреляции R_y(τ), интервала корреляции Δτ_y^кор, при этом числовые характеристики входного сигнала x(t) известны. Следует отметить, что нахождение W(y) очень сложная задача и требует особого рассмотрения.

Основой получения числовых характеристик служит коэффициент передачи цепи K(iω). Матожидание выходного сигнала определяется как:

m_y = K(ω=0) m_x,

Спектральная плотность мощности сигнала y(t):

G_y (ω) = K²(iω)G_x (ω) (9.1)

Выражение (9.1) является основной для нахождения числовых характеристик на выходе цепи. Функция корреляции:



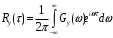
дисперсия выходного сигнала

σ_y² = R(0)

интервал корреляции выходного сигнала



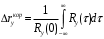
Полоса сигнала на выходе цепи определяется полосой пропускания самой линейной цепи:



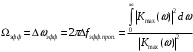
Для узкополосных радиотехнических цепей существует утверждение, что при любой плотности распределения вероятностей входного воздействия, но при условии, что полоса пропускания цепи много меньше эффективной полосы входного сигнала Ω_{эфф. проп.}<< Δω_{х эфф}, то происходит нормализация выходного сигнала, а именно, плотность распределения мгновенных значений подчиняется нормальному закону:

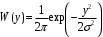(9.2)

Выражение (9.2) хорошо согласуется с теоремой Ляпунова, где доказано, что вероятностные характеристики входного процесса могут вообще любыми.

9.2 Прохождение случайного сигнала через нелинейные

---

безынерционные радиотехнические цепи.

Анализ воздействия случайного сигнала на линейную систему представляет трудную задачу, но для случая, когда выходной сигнал в данный момент однозначно определяется входным сигналом, то задача разрешимая.

Пусть задана характеристика нелинейного элемента y = f(x) и плотность распределения вероятностей входного воздействия W(x). Необходимо определить плотность распределения вероятностей мгновенных значений выходного сигнала W(y).

Рассмотрим случай одномерной плотности распределения вероятностей случайной величины. Плотность распределения вероятностей W(x) случайной величины известна, функционал нелинейной цепи задан: y = f(x).

Предположим, что существует однозначная обратная функция x = φ(y). Поскольку случайные величины x(t) и y(t) связаны однозначной функциональной зависимостью, то из того, что x₁ заключено в достаточно малом интервале (x₁ , x₁ +dx) следует, что и y₁ будет находиться в интервале (y₁ , y₁ +dy), где y₁=f(x₁), а сами вероятности равны произведению плотности вероятности на dx или dy, как показано на рисунке 9.2.



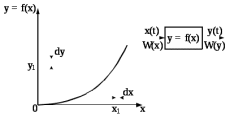
Рис. 9.2 – К определению плотности распределения вероятности W(y) на выходе нелинейной цепи

Как следует из вышесказанного W(x)dx = W(y)dy.

В результате получаем

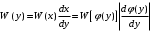(9.3)

Поскольку плотности вероятностей могут быть отрицательными, то в формулу (9.3) следует поставить модуль производной.



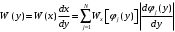
Таким образом, при воздействии случайного процесса на нелинейную систему изменяется спектр мощности процесса, законы распределения вероятностей и все связанные с ними параметры (матожидание, дисперсия и т.д.).

9.3 Контрольные вопросы и задачи

9.3.1 Определить матожидание случайного процесса на выходе RC-интегратора, на вход которого поступает сигнал с матожиданием равному 2.

9.3.2 Определить спектральную плотность мощности сигнала G_RCна выходе RC интегратора, если на вход поступает сигнал типа «белого шума» со спектральной плотностью

---

N.

9.3.3 Определить функцию корреляции случайного процесса со спектральной плотностью мощности, определенной в задаче 9.3.2.

9.3.4 Чем объяснить нормализацию случайного сигнала на выходе линейного инерционного устройства при воздействии на его входе произвольного случайного сигнала

9.3.5 Как изменяются свойства случайного сигнала с нормальным законом распределения в результате его преобразования в линейном устройстве?

9.3.6 Каким образом определяется одномерная плотность распределения вероятностей случайного сигнала на выходе нелинейного безынерционного устройства?

9.3.7 Случайный сигнал, корреляционная функция которого B(τ) = exp(-aτ) воздействует на вход линейного инерционного устройства с АЧХ:



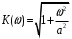
Определить и построить график корреляционной функции на выходе устройства.

9.3.8 Задан сигнал вида у = Acosx, где случайная величина х распределена равномерно в диапазоне -π от до +π. Найти плотность распределения вероятностей величины у.

9.3.9 На вход безынерционного устройства, характеристики которых приведены на рисунке 9.3, действует стационарный гауссовский шум x(t) с нулевым математическим ожиданием. Определить плотность распределения вероятностей W(y) шума y(t) на выходе устройства.



Рис.9.3 - Функциональные зависимости безынерционного устройства

9.3.10 Определить спектральную плотность мощности сигнала G_RCна выходе RC дифференциатора, если на вход поступает сигнал типа «белого шума» со спектральной плотностью N.

10 Огибающая и фаза узкополосного случайного сигнала.

10.1 Аналитический сигнал

Детерминированные и случайные процессы обычно представляются действительными функциями времени x(t). Вместе с тем, часто удобнее представлять их векторами на комплексной плоскости в теории электрических цепей символической записи синусоидальных колебаний. Практическое значение комплексного представления случайных сигналов: оно позволяет представить любой случайный процесс в виде гармонического колебания со случайной амплитудой огибающей E(t) и фазой θ(t).

Действительная функция:

---

x(t) = E(t) cos(ω₀t – φ₀) = E(t) cos[Θ(t)] (10.1)
гдеΘ(t) – полная фаза,E(t) – огибающая амплитуда,ω₀ - мгновенная частота,φ₀ – начальная фаза.

В символической форме выражение (10.1) может быть представлено следующим образом:






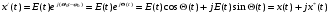
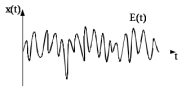
Рис.10.1 – Пример огибающей случайного процесса

Иначе говоря, символическое представление x(t)получается добавле­нием к действительной части x(t)=E(t)cosθ(t) определенным образом подоб­ранной мнимой частиx*(t)=E(t)sinθ(t).

Последняя выбирается так, чтобы проекция x^/(t) на ось абсцисс соответст­вовала исходной действительной функции Re[x^/(t)]=x(t)



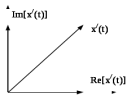
Рис.10.2 - Разложение СП на ортогональные составляющие x^/(t)
В нашем случае мнимая часть Im[x^/(t)]= x^*(t) колебания x^/(t) находится в квадратуре (сдвинута на угол π/2 ) с действительной частью x^/(t) .

Комплексный вектор 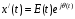длиной E вращается с угловой скоростью 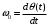против часовой стрелки; конец вектора описывает окруж­ность.

Функции x(t) и x^*(t) называются сопряженными по Гильберту. Доказано, что действительная и мнимая составляющая функции связаны между собой па­рой взаимно однозначных интегральных преобразований Гильберта:

Прямое преобразование Гильберта [13]:

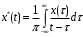
Обратное преобразование Гильберта




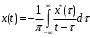
Аналогично для функции sinω₀t сопряженной является функция cosω₀ t, как показано на рисунке 10.3.



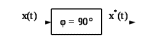
Рис.10.3 - Получение сопряженного сигнала по Гильберту для гармонического сигнала

---

Смотрите также файлы

• Требования к выполнению реферата.doc

• Предмет, метод и система земельного права. Предметом.docx

• Дипломная работа содержание введение.docx

• Самовосстанавливающегося предохранителя.docx

• Прямая на плоскости и в пространстве.doc