Во-первых, гармонические сигналы не меняют свою форму при прохождения стационарных линейных электрических цепей. Сигнал на выходе такой цепи останется гармоническим с той же частотой, не изменяя форму, а отличаясь от входного, лишь амплитудой и начальной фазой.

Во – вторых, устройства генерирования таких сигналов, довольна просты.

Представление любого сигнала в виде суммы гармонических колебаний с различными частотами, различными амплитудами и начальными фазами, то говорят, что осуществлено спектральное разложение этого сигнала.
1.2.1 Спектральное представление периодического сигнала
Математической моделью процесса, повторяющегося во времени, является периодический сигнал S(t), обладающий следующим свойством:
S(t) = S(t+nT),
где n =1,2,3, . . , T – период повторения сигнала (рис1.2)




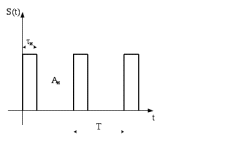
Рис. 1.2 - Периодическая последовательность импульсов
Согласно свойству периодичности, необходимо найти спектральное разложение сигнала, то есть найти составляющие, при сложении которых, можно восстановить форму исходного сигнала до его разложения.

В качестве спектральных составляющих воспользуемся рядом Фурье, представленного в таблице 1.1
Таблица 1.1 Набор ортогональных функций Фурье

1			. . . . . . . . . . .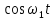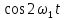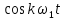
			. . . . . . . . . . .

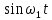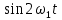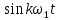Ортогональность функций Фурье означает, что скалярное произведение этих функций на интервале ортогональности равно нулю:

---

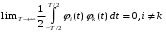(1.1).

Введем основную частоту 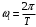последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения, запишем ряд Фурье для периодического сигнала:

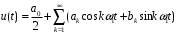(1.2)

с коэффициентами:

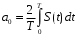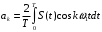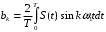, , (1.3)

В общем случае периодический сигнал содержит постоянную составляющую и бесконечный набор гармоник с частотами

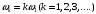кратными основной частоте последовательности.

Каждую гармонику можно описать её амплитудой А_k и начальной фазой 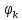. Для этого коэффициенты Фурье запишем следующим образом: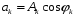



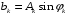
так что:





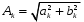
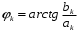
Подставляя эти выражения в (1.2), получим другую, эквивалентную форму ряда Фурье, для которой и будем строить спектр сигнала S(t) посредством u(t), но более удобным способом:



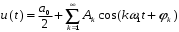
В данном рассмотрении, u(t) и S(t) это один и тот же сигнал, но только при 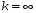. При меньших k, аппроксимирующий сигнал u(t) воспроизводит форму S(t), только с погрешностью. В некоторых случаях для анализа достаточно иметь спектр и при небольших k.

Итогом спектрального анализа является спектральная диаграмма периодического сигнала, которую принято называть графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы (рис. 1.3) и (рис.1.4).


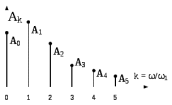
Рис.1.3 – Амплитудная спектральная диаграмм некоторого периодического сигнала


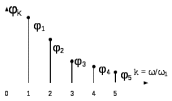
Рис.1.4 – Фазовая спектральная диаграмма периодического сигнала

---

Здесь по горизонтальной оси в некотором масштабе отложены номера гармоник, а по вертикальной оси представлены амплитуды и начальные фазы. Больший интерес представляет амплитудная диаграмма, которая позволяет судить о процентном содержании тех или иных гармоник в спектре периодического сигнала.

Для примера определим ряд Фурье периодической последовательности прямоугольных импульсов с известными параметрами: длительностью импульса 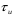, периодом повторения Т и амплитудой А, четной относительно начала отсчета (рис.1.5).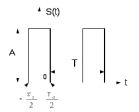



Рис. 1.5 – Импульсная последовательность прямоугольных импульсов.

По формуле (1.3), находим коэффициенты Фурье, где 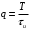- скважность.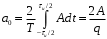







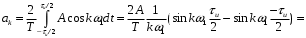
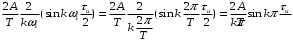
Окончательную форму ряда Фурье удобно представить как:

---

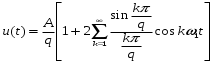
1.2.2 Комплексная форма представления ряда Фурье

Спектральное разложение периодического сигнала можно выполнить с использованием базисных функций, состоящую из экспонент с мнимыми показателями[1]:



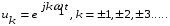
Как видно, функции этой системы периодичны с периодом Т и ортогональны на отрезке времени [-T/2, T/2]:



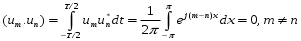
Ряд Фурье произвольного периодического сигнала в данном случае принимает вид:

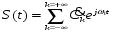(1. 4)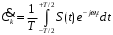



Выражение (1.4) представляет собой ряд Фурье в комплексной форме.

Спектр сигнала в соответствии с выражением (1.3) содержит компоненты на отрицательной полуоси частот 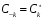. В рассматриваемом ряде слагаемые с положительными и отрицательными частотами объединяются в пары, например: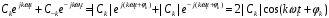



Таким образом, отрицательная частота - это понятие не физическое, а математическое, вытекающего из способа представления комплексных чисел.
1.2.3 Спектр непериодического сигнала
Рассмотрим спектральные характеристики непериодического сигнала, используя ряд Фурье.

Пусть S(t) – одиночный импульсный сигнал конечной длительности. Добавим к нему такой же сигнал через интервал повторения Т, и сделав его как бы периодическим. В результате получим рассмотренный ранее периодический сигнал в виде последовательности импульсов S_пер.(t). Представим образованный сигнал в виде комплексного ряда Фурье:



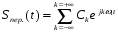
с коэффициентами:

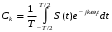(1.5)

Для того, чтобы вернуться к одиночному импульсу, устремив период повторения к бесконечности 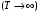и рассмотрим, что произойдет с формулой (1.5). При этом очевидно:

1. 
   Частоты соседних гармоник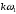 и 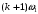окажутся сколь угодно близкими, поэтому можно произвести замену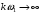
   
2. 
   Амплитудные коэффициенты C_kстанут неограниченно малыми из-за того, что в знаменателе находится величина Т.
   

---

Таким образом, необходимо найти предельное значение вида формулы (1.5) при .

Примем во внимание, что коэффициенты ряда Фурье образуют комплексно-сопряженные пары:



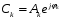
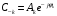
Каждой такой паре отвечает гармоническое колебание:


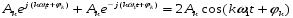
с комплексной амплитудой .

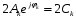Рассмотрим малый интервал частот Δω, образующий окрестность некоторого выбранного значения 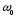. В пределах этого интервала будет содержаться 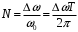отдельных пар спектральных составляющих, частоты которых отличаются сколь угодно незначительно. Поэтому составляющие можно складывать так, как будто все они имеют одну и туже частоту и характеризуются одинаковыми комплексными амплитудами: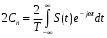



В результате находим комплексную амплитуду эквивалентного гармонического сигнала, отображающего вклад всех спектральных составляющих, содержащих внутри интервала Δω:

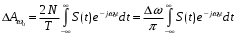
Таким образом мы получаем спектральную плотность сигнала S(t):
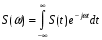(1.6).

Формула (1.6) осуществляет преобразование Фурье данного сигнала. При этом важно отметить, что спектральная плотность сигнала – комплексная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе элементарных синусоид.

С другой стороны, нахождение сигнала по спектральной плотности сводится к обратному преобразованию Фурье:
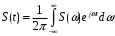(1.7)
Отсюда следует фундаментальный результат: сигнал S(t) и его спектральная плотность S(ω) взаимно-однозначно связаны прямым и обратным преобразованием Фурье:

---

Смотрите также файлы

• Требования к выполнению реферата.doc

• Предмет, метод и система земельного права. Предметом.docx

• Дипломная работа содержание введение.docx

• Самовосстанавливающегося предохранителя.docx

• Прямая на плоскости и в пространстве.doc