7.3.8 Построить спектр АМ-сигнала на входе нелинейного элемента, на его выходе и на выходе фильтра нижних частот детектора (линейное детектирование).

7.3.9 Определить коэффициент нелинейных искажений на выходе квадратического детектора при глубине модуляции, равной 0,8.

7.3.10 Перечислить недостатки ЧМ-модулятора на варикапе и приемы их устранения.

7.3.11 Привести принципиальную схему и характеристику детектирования ЧМ-сигнала на одном расстроенном контуре, а также показать временные диаграммы в различных точках схемы. Перечислить достоинства и недостатки детектирования на одном расстроенном контуре.

7.3.12 Привести принципиальную схему и характеристику детектирования ЧМ-сигнала на двух расстроенных контурах, а также показать временные диаграммы в различных точках схемы.

8. 
   Спектральный анализ случайных процессов
   

1. 
   Спектральная плотность мощности случайных процессов
   

Из-за вероятностного характера отдельных реализаций прямой перенос методов спектрального анализа в теорию случайных процессов невозможен. Однако удается получить ряд важных спектральных характеристик случайных колебаний, преобразуя по Фурье некоторые функции, получаемые путем усреднения реализаций.

Рассмотрим стационарный случайный процесс X(t) с нулевым математическим ожиданием, равным нулю. Отдельно взятая реализация этого процесса есть детерминированная функция, которую можно представить в виде обратного преобразования Фурье

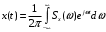(8.1)

с некоторой детерминированной спектральной плотностью S_x (ω).

Для того, чтобы описать весь ансамбль реализаций, образующий процесс X(t), естественно допустить, что спектральные плотности S_x (ω) сами являются случайными функциями частоты. Таким образом, случайный процесс во временной области порождает другой случайный процесс в частотной области. Если реализация случайного процесса представлена в форме (8.1), то говорят, что осуществлено спектральное представление этого процесса.

Рассмотрим основное свойство спектральной плотности. Определим при каких условиях функция корреляции

---

R_x(τ) зависит лишь от сдвига τ между сечениями. Воспользуемся тем, что сигнал x(t) вещественный, так что наряду c (8.1) справедливо равенство

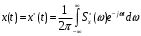(8.2)

Запишем выражение функции корреляции процесса x(t), используя спектральные разложения случайных реализаций

=
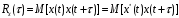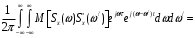(8.3)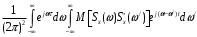


Здесь во внутреннем подынтегральном выражении содержится множитель M[S_x(ω)S_x^*(ω)], имеющей смысл функции корреляции случайной спектральной плотности. Для того, чтобы функция R_x(τ) не зависела от времени t, необходимо, как это видно из выражения (8.3), потребовать выполнения следующей пропорциональности:

M[[S_x(ω)S_x^*( ώ)] δ(ω – ώ).(8.4)

Таким образом, значения спектральной плотности соответствующие любым двум несовпадающим частотам, не коррелированы между собой.

Введем в формулу (8.4) множитель пропорциональности, зависящий от частоты, и запишем это равенство как:

M[S_x (ω)S_x^*(ω)] = 2πG_x(ω)δ(ω-ώ). (8.5)

Функция G_x(ω), играющая фундаментальную роль в теории случайных процессов, называется спектральной плотностью мощности процесса X(t), в дальнейшем спектром мощности.

Подставив (8.5) в (8.3), приходим к важному результату:

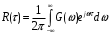(8.6)

Итак, функция корреляции и спектр мощности стационарного случайного процесса связаны между собой преобразованием Фурье:

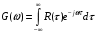(8.7)

Формулы (8.6) и (8.7) составляют содержание теоремы, доказанной в 1934 году известным советским математиком А.Я. Хинчиным и независимо от него американским ученым Н.Винером. Данная теорема в теории случайных процессов получила название теоремы Винера-Хинчина.

Для понимания физического смысла G(ω), в (8.6) положим τ = 0. Тогда, поскольку R(0) = σ², получаем:

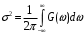(8.8)

Дисперсия σ², равная средней мощности флуктуаций случайного стационарного процесса, есть, таким образом, сумма вкладов от всех участков частотной оси. Кроме того, спектр мощности величина положительная и накладывает жесткие ограничения на вид допустимых функций корреляции.

---

Спектр мощности не содержит никакой информации о фазовых соотношениях между отдельными спектральными составляющими. Поэтому принципиально невозможно восстановить какую-либо отдельно взятую реализацию случайного процесса.

Поскольку R(τ) - четная функция аргумента τ, то соответствующий спектр мощности G(ω) представляет собой четную функцию частоты ω. Отсюда следует, что пару преобразований Фурье (8.6), (8.7) можно записать, используя лишь интегралы в полу бесконечных пределах:





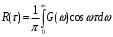
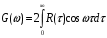
Случайные процессы, изучаемые статистической радиотехникой, как правило, обладают следующим свойством: их функция корреляции стремится к нулю с увеличением временного сдвига τ. Чем быстрее убывает функция, тем меньшей оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающих момента времени.

Числовой характеристикой, служащей для оценки «скорости изменения» реализаций случайного процесса, является интервал корреляции τ_к, определяемый как:

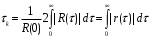(8.9)

Если известна информация о поведении какой-либо реализации «в прошлом», то возможен вероятностный прогноз случайного процесса на время порядка τ_к. Прогнозирование на время больше интервала корреляции, бессмысленно, так как мгновенные значения становятся не коррелированы.

Эффективная ширина спектра определяется на основе следующего равенства:

,

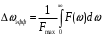где F(ω) = G(ω)/π – односторонняя спектральная плотность мощности.

Величины τ_к и Δω_эфф. связаны соотношением неопределенности:

τ_к Δω_эфф = const,

вытекающим из свойств преобразования Фурье.

В радиотехнике белым шумом принято стационарный случайный процесс с постоянной на всех частотах спектральной плотность мощности:

G(ω) = G(0) = const.

Термин «белый шум» образно подчеркивает сходство с «белым» светом, у которого в пределах видимого диапазона интенсивность всех спектральных составляющих приблизительно одинакова.

По теореме Винера-Хинчина функция корреляции белого шума:

---

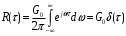
Равна нулю всюду, кроме точки τ =0. Средняя мощность белого шума неограниченно велика. Белый шум является дельта-коррелированным случайным процессом. Некоррелированность мгновенных значений такого случайного процесса означает бесконечно большую скорость изменения их во времени – как бы мал ни был интервал τ, сигнал за это время может измениться на любую наперед заданную величину.

Белый шум является абстрактной математической моделью и отвечающий ему физический процесс в природе, безусловно, не существует. Однако это не мешает приближенно заменять реальные достаточно широкополосные случайные процессы белым шумом в тех случаях, когда полоса пропускания цепи, на которую воздействует случайный сигнал, оказывается существенно уже эффективной ширины спектра шума.

8.2 Узкополосные и широкополосные сигналы.

Спектральная плотность мощности реальных процессов практически ограничена полосой частот Δω = ω_в - ω_н, поэтому в дальнейшем удобно разделить случайные процессы на широкополосные и узкополосные. Случайный процесс называется узкополосным, если спектральная плотность мощности сосредоточена в сравнительно узкой полосе, то есть значения частот значительны, а полоса небольшая: ω_o >> Δω = ω_в - ω_н , где ω_o = Δω/2. Случайный процесс называется широкополосным, если и полоса Δω и величина частот ω_o соизмеримы, а именно ω_o ≈ Δω.

Рассмотрим широкополосный сигнал на примере белого шума, ограниченного полосой от 0 до ω_в, или другими словами, прохождение случайного процесса с равномерной спектральной плотностью мощностиG(ω)=N₀ через идеальный фильтр, как показано на рисунке 8.1.



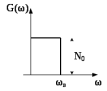
Рис. 8.1 - Спектральная плотность мощности узкополосного случайного процесса, ограниченного частотой ω_в

Для данного случайного процесса определим функцию корреляции по теореме Винера - Хинчина:



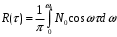
после интегрирования получим:

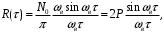где 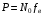(8.10)

На рисунке 8.2 показана функция корреляции широкополосного сигнала типа белого шума.

---

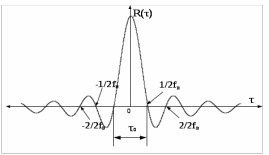
Рис. 8.2 – Функция корреляции белого шума, ограниченного частотой ω_в.

При данном виде графика функции корреляции (рисунок 8.2) за интервал корреляции τ₀ можно принять Δτ между двумя первыми нулями, а именно:



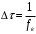
Из этого соотношения видно, что по мере сокращения полосы частот Δω = ω_в, интервал корреляции увеличивается. Таким образом, ограничение спектра влечет за собой увеличение корреляции между мгновенными значениями случайного процесса.

Определим функцию корреляции узкополосного случайного процесса для равномерно распределенной спектральной плотности мощности по оси частот, как показано на рисунке 8.3.



Рис.8.3 – Спектральная плотность мощности узкополосного случайного процесса, типа белого шума, ограниченного идеальным полосовым фильтром

Функция корреляции узкополосного случайного процесса с равномерной спектральной плотности мощности:



= ,

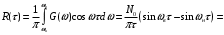
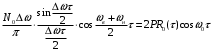где , ,

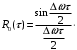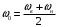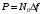
На рисунке 8.4 показана корреляционная функция, построенная в соответствии с приведенными выше выражениями.



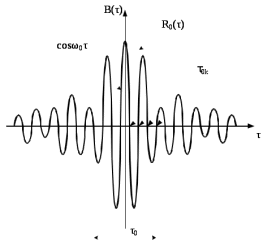
Рис.8.4 – Функция корреляции узкополосного случайного процесса с равномерной спектральной плотностью мощности

Для узкополосного случайного процесса характерен тот факт, что интервал корреляции для него двоякий, для огибающей R₀ (τ) и для заполнения вида

cos ω₀τ. Таким образом, для огибающей τ₀ = 1/Δf и для заполнения τ_0k = (2k+1)/4f₀.

---

Смотрите также файлы

• Требования к выполнению реферата.doc

• Предмет, метод и система земельного права. Предметом.docx

• Дипломная работа содержание введение.docx

• Самовосстанавливающегося предохранителя.docx

• Прямая на плоскости и в пространстве.doc