Ещё пример задания:

Р-19. Логическая функция F задаётся выражением

((w  y)  x)  ((w  z)  (y  w)).

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

?	?	?	?	F
1			1	0
			1	0
1		1		0

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение:

1. 
   запишем выражение в более понятной форме: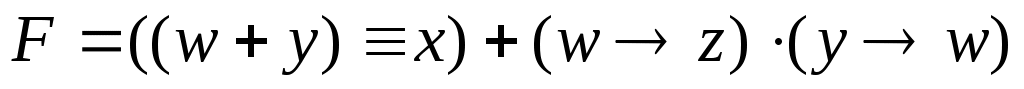
   
2. 
   попробуем найти все сочетания переменных, при которых функция равна 0 (их должно быть не очень много)
   
3. 
   выберем для начальной подстановки переменную, которая чаще всего встречается в выражении и поэтому подстановка её значения даст наибольшую информацию; у нас это переменная w
   
4. 
   подставим сначала w = 0, а затем w = 1, и таким образом построим все строки таблицы истинности, где функция равна нулю
   
5. 
   при w = 0 получаем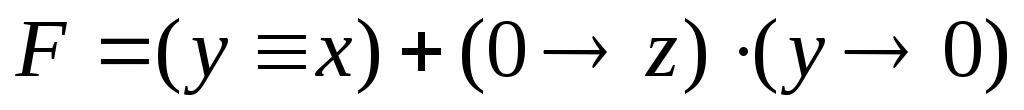
   

поскольку при всех z, имеем

6. 
   для того, чтобы сумма была равна 0, оба слагаемых должны быть равны 0, так что
   

---

7. 
   таким образом, при w = 0 получаем y = 1, x = 0, а значение z может быть любое; это даёт две строки в таблице истинности:
   

   x	y	z	w	F
   0	1	0	0	0
   0	1	1	0	0

8. 
   теперь рассмотрим случай, когда w = 1: получаем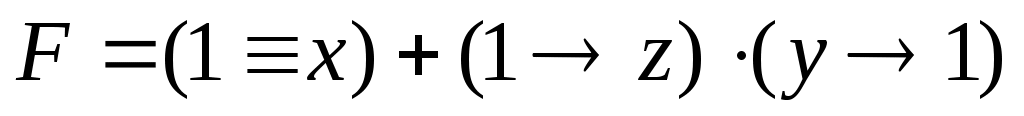
   

поскольку при всех y, имеем

9. 
   для того, чтобы сумма была равна 0, оба слагаемых должны быть равны 0, так что
   

10. 
    таким образом, при w = 1 получаем x = 0, z = 0, а значение y может быть любое; добавляем ещё две строки в таблицу истинности:
    

    x	y	z	w	F
    0	1	0	0	0
    0	1	1	0	0
    0	0	0	1
    0	1	0	1

11. 
    сравниваем эту таблицу с таблицей в задании:
    

    1	2	3	4	F
    1			1	0
    			1	0
    1		1		0

12. 
    две единицы могут быть только в столбцах y и w, поэтому это столбцы 1 и 4
    
13. 
    кроме этих столбцов единственная единица может быть в столбце z, поэтому столбец 3 – это z
    
14. 
    при z = 1 должно быть y = 1, поэтому столбец 1 – это y, а столбец 4 – это w
    
15. 
    остаётся столбец 2 – это x
    
16. 
    Ответ: yxzw.
    

---

Решение (разбиение на два слагаемых, А.Н. Носкин):

1. 
   запишем выражение в более понятной форме:
   
2. 
   Каждое из слагаемых скобок должна быть равна 0, поэтому составим для каждой таблицу истинности.
   
3. 
   Рассмотрим ((w  z)  (y  w)), а именно первую скобку (w  z), она равна 0 при ситуации 1  0, тогда y во второй скобке может быть любым
   

w	z	y
1	0	0
1	0	1

Теперь рассмотрим вторую скобку (y  w), она равна 0 при ситуации 1  0, тогда zво первой скобке может быть любым. Добавим эти значения в таблицу истинности, которая приведена выше.

w	z	y
1	0	0
1	0	1
0	0	1
0	1	1

4. 
   Теперь рассмотрим ((w  y)  x). Эта скобка будет равна 0 при ((w  y) ≠ x). Составим таблицу истинности
   

w	y	x
0	0	1
1	0	0
0	1	0
1	1	0

Анализ этой таблицы показывает, что набора 001 (выделено цветом) быть не может иначе система будет равна 1 по скобке ((w  z)  (y  w)).

5. 
   Сравним полученные таблицы истинности с исходной таблицей в задании:
   

   1	2	3	4	F
   1			1	0
   			1	0
   1		1		0

6. 
   x в таблице истинности во всех строках равен 0, тогда он соответствует второму столбцу, так как там нет ни одной единицы. Сразу заполним нулями.
   

   1	x	3	4	F
   1	0		1	0
   	0		1	0
   1	0	1		0

7. 
   w и y в таблице истинности имеют 2 и более единицы, а z всего 1, тогда z - это столбец 3. Заполним сразу 0.
   

---

1	x	z	4	F
1	0	0	1	0
	0	0	1	0
1	0	1		0

8. 
   Так как строки не повторяются, то в первой ячейке второй строки может быть только 0. Заполним ее.
   

1	x	z	4	F
1	0	0	1	0
0	0	0	1	0
1	0	1		0

9. 
   Теперь проанализируем последнюю ячейку третьей строки. Ее значения могут быть 0 и 1. Предположим, что там 0, а в первом столбце w, тогда выражение примет вид
   

((1  0)  0)  ((1  1)  (0  1)) – этого быть не может, так как выражение равно 1. Предположим, что там 1 и в первом столбце w, тогда выражение примет вид

((1  1)  0)  ((1  1)  (1  1)) – этого быть не может, так как выражение равно 1. Таким образом в первом столбце w не может быть ни при каком случае. Там только y, ну а w отправляется в 4-й столбец.

10. 
    Ответ: yxzw.
    

Решение (построение таблицы с помощью программы, Б.С, Михлин)

print('x y z w') # заголовок таблицы

k = 0, 1 # k - кортеж констант (0 - False, 1 - True)

for x in k:

for y in k:

for z in k:

for w in k:

if not (((w or y) == x ) or (not w or z) and \

(not y or w) ) :

# можно так:

# if ( ( ( w or y ) == x ) or ( not w or z) \

# * (not y or w) ) == 0: # '*' вместо ‘and’

print( x, y, z, w ) # если F = 0

---

Ещё пример задания:

Р-18. Логическая функция F задаётся выражением (x  y)  (y  z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

?	?	?	F
0	0		0
0			0

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение:

1. 
   запишем выражение в более понятной форме: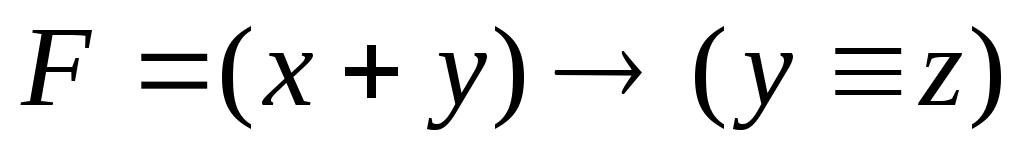
   
2. 
   для решения этой задачи используем свойство операции «импликация»: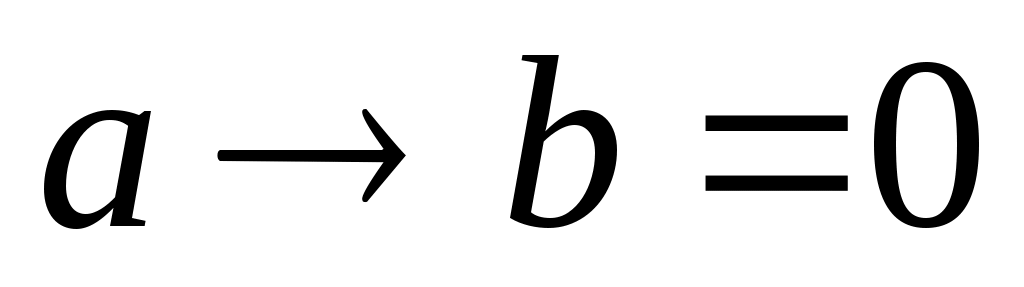 тогда и только тогда, когда a = 1 и b = 0
   
3. 
   в обеих строках приведённой части таблицы функция равна 0, поэтому везде
   

• 
  хотя бы одна из величин, x или y равна 1, что даёт ;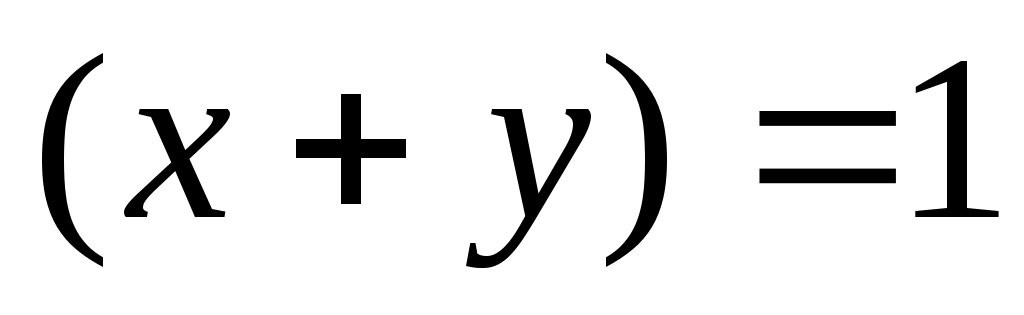
  
• 
  y и z различны, что даёт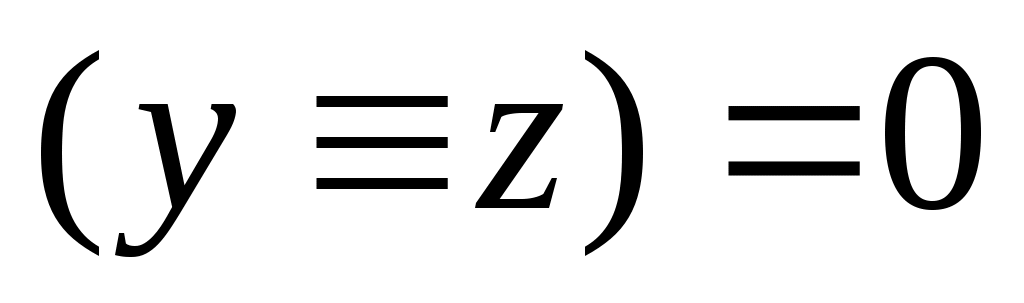
  

4. 
   поскольку значения в первых двух столбцах в первой строке равны 0, один из этих столбцов – это x
   
5. 
   предположим, что x – это первый столбец:
   

	x	?	?	F
1	0	0		0
2	0			0

тогда в обеих строках получаем

---

Смотрите также файлы

• А) отдельных категорий административных дел (разд. Iv.pdf

• Конспект содержания программы Инклюзивное и интегративное образование детей с овз в условиях введения и реализации фгос ноо овз.doc

• 13. 03. 02 Электроэнергетика и электротехника.docx

• Искусственный интеллект его возможности и потенциал.docx

• Анализ содержания организации и руководства игровой деятельности детей дошкольного возраста в режиме дня доо в группах детей раннего, младшего и старшего дошкольного возраста..docx