Файл: Тема урока Решение задач с помощью квадратных уравнений Класс 8 Тема урока Решение задач с помощью квадратных уравнений. Цели урока Образовательные формирование познавательных ууд.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.Сколько корней имеет уравнение, если D > 0? D < 0? D = 0?
3. Реши уравнения: а) 5х2 + 8х – 4 = 0; б) х2 – 6х + 11 = 0; в) 7х2 + 6х – 1 = 0.
Ответ: а) 2/5, -2; б) корней нет; в) 1/7, -1.
Два ученика получают карточку с задачей, решают у доски.
Карточка №1
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 156. Найдите эти числа.
Решение: Пусть первое натуральное число равно х, тогда второе число х+1. По условию задачи произведение чисел равно 156. Получаем уравнение:
х×(х+1) = 156,
х2 + х – 156 = 0,
D=1+624=625,
 =
=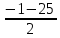 =-13,
=-13,  =
=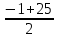 =12.
=12.
Так как х натуральное число, то -13 посторонний корень. Значит одно из чисел 12, а другое 12+1=13
Ответ: 12; 13.
Карточка № 2
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 210. Найдите эти числа.
Решение: Пусть х первое натуральное число, тогда х+1 – второе число. По условию задачи произведение чисел равно 210. Получаем уравнение:
х×(х+1)=210,
х2 + х – 210=0,
D=1+840=841,
 =
=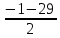 =-15,
=-15, 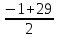 =14.
=14.
Так как х – натуральное число, то- 15 – посторонний корень, значит первое число равно 14, а второе 14+1=15.
Ответ: 14; 15.
Остальные учащиеся по вариантам, выполняют практическое задание. Задание на доске.
1.Вариант
1) 3х2 – 7х = 0;
Ответ: =0,
=0,  =2
=2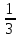 .
.
2) 2х2 – х = 0;
Ответ: =0,
=0,  =
= .
.
3) х2 – 2х + 1 = 0;
Ответ: =0.
=0.
4) х2 + 3х + 3 = 0;
Ответ: корней нет.
2 вариант
1) 5х2 + 14х – 3 = 0;
Ответ:
=-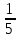 ,
,  =-3.
=-3.
2) 7х2 + 8х + 1 = 0;
Ответ: =-1,
=-1,  =-
=-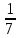 .
.
3) х2 – 2х + 2 = 0;
Ответ: корней нет.
4) 3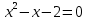 ;
;
Ответ: =1,
=1,  =-
=-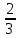 .
.
В конце работы проводится взаимопроверка между рядами.
4. Формирование умений составлять уравнения по условию задачи.
На прошлом уроке мы узнали, что многие задачи алгебры, приводят к необходимости решения квадратного уравнения. Давайте вспомним алгоритм решения задачи с помощью квадратного уравнения.
Этапы решения задачи алгебраическим методом:
1. Выбрать неизвестно.
2. Затем составить уравнение.
3. Решить его.
4. Сделать вывод о корнях.
5. Выполнить дополнительные действия.
А теперь давайте потренируемся в составлении уравнений по условию задачи, а также закрепим навык решения квадратных уравнений с помощью небольшого тренажера. Ученикам самостоятельно предлагается решить задачи и выбрать правильный вариант ответа. Если ученик затрудняется решить задачу, он может попросить помощи ученика-консультанта или учителя.
Задания на доске.
1. Составьте уравнение к задаче, приняв за х меньшее из чисел: Произведение двух натуральных чисел, одно из которых на 5 больше другого, равно 256. Найдите эти числа.
1) х( х – 5) = 256; 2) х(х + 5) = 256; 3) 2х2 + 5 = 256; 4) 2х – 5 = 256.
Ответ: х(х+5)=256.
2. Составьте уравнение к задаче, приняв за х меньшее из чисел: Одна из сторон прямоугольника на 12 см больше другой. Площадь этого прямоугольника равна 405 см. Найдите стороны прямоугольника.
1) х( х + 12) = 405 2) х(х - 12) = 405 3)2х - 12 = 405 4) 2х + 12 = 405
Ответ: х(х+12)=405.
3. Составьте уравнение к задаче, приняв за х меньшее из чисел: Высота треугольника на 4 см меньше основания этого треугольника, его площадь равна 48 . Найдите высоту треугольника.
. Найдите высоту треугольника.
1) х( х + 4) = 48 2) - 4 = 96 3) х(х - 4) = 48 4) х(х + 4) = 96
- 4 = 96 3) х(х - 4) = 48 4) х(х + 4) = 96
Ответ: х(х+4)=96.
4. Решите задачу. В прямоугольном треугольнике один катет больше другого на 3 см, а гипотенуза равна 15 см. Найти длину меньшего катета треугольника.
Чтобы правильно ученики составили уравнение. Необходимо вспомнить теорему Пифагора.
Решение: +
+ 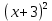 =
=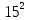 ,
,
 +
+ +6х+9=225,
+6х+9=225,
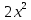 +6х+9-225=0,
+6х+9-225=0,
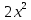 +6х-216=0, разделим на 2
+6х-216=0, разделим на 2
 +3х-108=0,
+3х-108=0,
D=9+432=441,
 =
=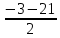 =-12,
=-12,  =
=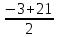 =9.
=9.
Корень уравнения -12 условию задачи не удовлетворяет, значит, меньший катет равен 9 см.
1) 9 см 2) 6 см 3) 5 см 4) 12 см.
5. Решите задачу. Сумма смежных сторон прямоугольника равна 17 см, а его диагональ 13 см. Найти стороны прямоугольника.
Решение: Проведенная диагональ, делит прямоугольник на два прямоугольных треугольника. Пусть х см длина наименьшего катета, тогда зная, сумму смежных сторон треугольника мы можем найти второй катет, он равен (17-х) см. По условию задачи проведенная диагональ является гипотенузой прямоугольного треугольника и равна 13 см. Применяя теорему Пифагора, составим уравнение: +
+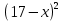 =
=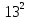 , раскроем скобки.
, раскроем скобки.
 +
+ -34х+289=169,
-34х+289=169,
 -34х+120=0, сократим на 2.
-34х+120=0, сократим на 2.
 -17х+60=0,
-17х+60=0,
D=289-240=49,
 =
=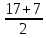 =12,
=12,  =
=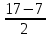 =5.
=5.
Оба корня удовлетворяют условию задачи. Значит, наименьший катет равен 5 см, а наибольший катет равен 12 см.
1) 3 см и 20 см 2) 8 см и 15 см 3) 12 см и 5 см 4) 8 см и 6 см
Проверим решение:
Правильные ответы на обратной стороне доски: 1) 2; 2) 1; 3) 4; 4) 1; 5) 3.
5. Изучение нового материала.
Часто алгебраические задачи решаются двумя способами. Например, решим задачу на движение двумя способами. Для этого вспомним:
- Какие величины связаны с движением?
- Как зависит расстояние от скорости и времени?
- Как найти скорость, если известны расстояние и время?
- Как найти время, если известны расстояние и время?
Задача № 1. (работа с классом)
Турист должен был пройти 6 км за определенный срок. Однако он задержался с выходом на 30 мин, поэтому, чтобы прийти вовремя, он шел со скоростью, превышающей намеченную на 1 км/ч. С какой скоростью шел пешеход?
Решение.
Первый способ.
Пусть х ч – намеченный срок. Вспомним! Ч
тобы найти скорость надо путь поделить на время, следовательно, 6/х км/ч – намеченная скорость. х – 0,5 ч – время, затраченное фактически, 6/(х – 0,5) км/ч – фактическая скорость. По условию задачи известно, что пешеход увеличил скорость на
1 км/ч.
Получаем уравнение: 6/(х – 0,5) – 6/х = 1.
Если х≠0,5 и х≠0, то 6х – 6х + 3 = х2 – 0,5х
2х2 – х – 6 = 0,
D=1+48=49,
 =
=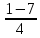 =-1,5
=-1,5  =
=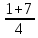 =2.
=2.
Так как время – положительное число, то – 1,5 не подходит. Намеченное время – 2 часа, а скорость, с которой шел пешеход – 6 : 2 + 1 = 4 (км/ч).
Ответ: 4 км/ч.
Второй способ.
Пусть х км/ч – намеченная скорость, тогда 6/х ч – намеченное время. х + 1 км/ч – фактическая скорость, 6/(х+1) ч – фактическое время. По условию задачи известно, что пешеход затратил времени на ½ часа меньше, чем планировал. Получаем уравнение: 6/х – 6/(х+1) = ½.
Если х ≠ 0, х ≠ 1, то 12х + 12 – 12х = х2 + х,
х2 + х – 12 = 0,
D=1+48=49,
 =
=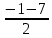 =-4,
=-4,  =
=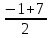 =3.
=3.
Так как скорость – положительное число, то – 4 не подходит, значит, намеченная скорость 3 км/ч, а скорость движения пешехода 3 + 1 = 4 (км/ч).
Ответ: 4 км/ч.
Задача № 2. (Самостоятельно, с оказанием дифференцированной помощи)
Велосипедист проехал с постоянной скоростью 40 км от пункта А до пункта В. Возвращаясь обратно со скоростью, на 10 км/ч меньшей первоначальной, он затратил на 20 мин больше, чем на путь от А до В. Найдите первоначальную скорость велосипедиста.
Проверим решение:
Первый способ
Пусть х км/ч – скорость велосипедиста при движении из пункта А в пункт В, тогда время движения – 40/х ч. На обратном пути он ехал со скоростью (х – 10) км/ч и затратил 40/(х - 10) ч. По условию задачи известно, что на обратный путь велосипедист затратил больше на 20 мин или на 1/3 часа. Получаем уравнение: 40/(х - 10) – 40/х = 1/3.
Если х ≠ 0, х ≠ 10, то 120х – 120х + 1200 = х2 – 10х,
х2 – 10х – 1200 = 0,
D=100+4800=4900,
 =
=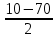 =-30,
=-30,  =
=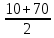 =40.
=40.
 = - 30 - условию задачи не удовлетворяет. Значит первоначальная скорость велосипедиста –
= - 30 - условию задачи не удовлетворяет. Значит первоначальная скорость велосипедиста –
40 км/ч.
Ответ: 40 км/ч.
Второй способ
Пусть х ч – время, затраченное велосипедистом на путь от А до В, тогда его скорость 40/х км/ч. Время, затраченное на обратный путь (х + 1/3) ч, а скорость – 40/(х + 1/3) км/ч. По условию задачи известно, что обратно велосипедист ехал со скоростью, на 10 км/ч меньшей первоначальной. Получаем уравнение: 40/х - 40/(х + 1/3) = 10.
Если х ≠ 0 и х ≠ 1/3, то 40(х + 1/3) – 40х = 10х(х + 1/3),
3х2 + х – 4 = 0,
D=1+48=49,
 =
=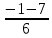 =-
=-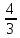 ,
,  =
=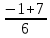 =1.
=1.
3. Реши уравнения: а) 5х2 + 8х – 4 = 0; б) х2 – 6х + 11 = 0; в) 7х2 + 6х – 1 = 0.
Ответ: а) 2/5, -2; б) корней нет; в) 1/7, -1.
Два ученика получают карточку с задачей, решают у доски.
Карточка №1
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 156. Найдите эти числа.
Решение: Пусть первое натуральное число равно х, тогда второе число х+1. По условию задачи произведение чисел равно 156. Получаем уравнение:
х×(х+1) = 156,
х2 + х – 156 = 0,
D=1+624=625,
 =
=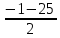 =-13,
=-13,  =
=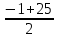 =12.
=12.Так как х натуральное число, то -13 посторонний корень. Значит одно из чисел 12, а другое 12+1=13
Ответ: 12; 13.
Карточка № 2
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 210. Найдите эти числа.
Решение: Пусть х первое натуральное число, тогда х+1 – второе число. По условию задачи произведение чисел равно 210. Получаем уравнение:
х×(х+1)=210,
х2 + х – 210=0,
D=1+840=841,
 =
=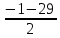 =-15,
=-15, 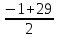 =14.
=14.Так как х – натуральное число, то- 15 – посторонний корень, значит первое число равно 14, а второе 14+1=15.
Ответ: 14; 15.
Остальные учащиеся по вариантам, выполняют практическое задание. Задание на доске.
1.Вариант
1) 3х2 – 7х = 0;
Ответ:
 =0,
=0,  =2
=2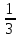 .
.2) 2х2 – х = 0;
Ответ:
 =0,
=0,  =
= .
.3) х2 – 2х + 1 = 0;
Ответ:
 =0.
=0.4) х2 + 3х + 3 = 0;
Ответ: корней нет.
2 вариант
1) 5х2 + 14х – 3 = 0;
Ответ:

=-
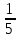 ,
,  =-3.
=-3.2) 7х2 + 8х + 1 = 0;
Ответ:
 =-1,
=-1,  =-
=-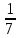 .
.3) х2 – 2х + 2 = 0;
Ответ: корней нет.
4) 3
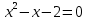 ;
;Ответ:
 =1,
=1,  =-
=-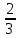 .
.В конце работы проводится взаимопроверка между рядами.
4. Формирование умений составлять уравнения по условию задачи.
На прошлом уроке мы узнали, что многие задачи алгебры, приводят к необходимости решения квадратного уравнения. Давайте вспомним алгоритм решения задачи с помощью квадратного уравнения.
Этапы решения задачи алгебраическим методом:
1. Выбрать неизвестно.
2. Затем составить уравнение.
3. Решить его.
4. Сделать вывод о корнях.
5. Выполнить дополнительные действия.
А теперь давайте потренируемся в составлении уравнений по условию задачи, а также закрепим навык решения квадратных уравнений с помощью небольшого тренажера. Ученикам самостоятельно предлагается решить задачи и выбрать правильный вариант ответа. Если ученик затрудняется решить задачу, он может попросить помощи ученика-консультанта или учителя.
Задания на доске.
1. Составьте уравнение к задаче, приняв за х меньшее из чисел: Произведение двух натуральных чисел, одно из которых на 5 больше другого, равно 256. Найдите эти числа.
1) х( х – 5) = 256; 2) х(х + 5) = 256; 3) 2х2 + 5 = 256; 4) 2х – 5 = 256.
Ответ: х(х+5)=256.
2. Составьте уравнение к задаче, приняв за х меньшее из чисел: Одна из сторон прямоугольника на 12 см больше другой. Площадь этого прямоугольника равна 405 см. Найдите стороны прямоугольника.
1) х( х + 12) = 405 2) х(х - 12) = 405 3)2х - 12 = 405 4) 2х + 12 = 405
Ответ: х(х+12)=405.
3. Составьте уравнение к задаче, приняв за х меньшее из чисел: Высота треугольника на 4 см меньше основания этого треугольника, его площадь равна 48
 . Найдите высоту треугольника.
. Найдите высоту треугольника.
1) х( х + 4) = 48 2)
 - 4 = 96 3) х(х - 4) = 48 4) х(х + 4) = 96
- 4 = 96 3) х(х - 4) = 48 4) х(х + 4) = 96Ответ: х(х+4)=96.
4. Решите задачу. В прямоугольном треугольнике один катет больше другого на 3 см, а гипотенуза равна 15 см. Найти длину меньшего катета треугольника.
Чтобы правильно ученики составили уравнение. Необходимо вспомнить теорему Пифагора.
Решение:
 +
+ 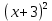 =
=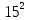 ,
, +
+ +6х+9=225,
+6х+9=225,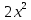 +6х+9-225=0,
+6х+9-225=0,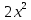 +6х-216=0, разделим на 2
+6х-216=0, разделим на 2 +3х-108=0,
+3х-108=0,D=9+432=441,
 =
=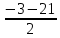 =-12,
=-12,  =
=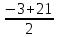 =9.
=9.Корень уравнения -12 условию задачи не удовлетворяет, значит, меньший катет равен 9 см.
1) 9 см 2) 6 см 3) 5 см 4) 12 см.
5. Решите задачу. Сумма смежных сторон прямоугольника равна 17 см, а его диагональ 13 см. Найти стороны прямоугольника.
Решение: Проведенная диагональ, делит прямоугольник на два прямоугольных треугольника. Пусть х см длина наименьшего катета, тогда зная, сумму смежных сторон треугольника мы можем найти второй катет, он равен (17-х) см. По условию задачи проведенная диагональ является гипотенузой прямоугольного треугольника и равна 13 см. Применяя теорему Пифагора, составим уравнение:
 +
+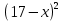 =
=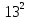 , раскроем скобки.
, раскроем скобки. +
+ -34х+289=169,
-34х+289=169, -34х+120=0, сократим на 2.
-34х+120=0, сократим на 2. -17х+60=0,
-17х+60=0,D=289-240=49,
 =
=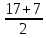 =12,
=12,  =
=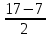 =5.
=5.Оба корня удовлетворяют условию задачи. Значит, наименьший катет равен 5 см, а наибольший катет равен 12 см.
1) 3 см и 20 см 2) 8 см и 15 см 3) 12 см и 5 см 4) 8 см и 6 см
Проверим решение:
Правильные ответы на обратной стороне доски: 1) 2; 2) 1; 3) 4; 4) 1; 5) 3.
5. Изучение нового материала.
Часто алгебраические задачи решаются двумя способами. Например, решим задачу на движение двумя способами. Для этого вспомним:
- Какие величины связаны с движением?
- Как зависит расстояние от скорости и времени?
- Как найти скорость, если известны расстояние и время?
- Как найти время, если известны расстояние и время?
Задача № 1. (работа с классом)
Турист должен был пройти 6 км за определенный срок. Однако он задержался с выходом на 30 мин, поэтому, чтобы прийти вовремя, он шел со скоростью, превышающей намеченную на 1 км/ч. С какой скоростью шел пешеход?
Решение.
Первый способ.
Пусть х ч – намеченный срок. Вспомним! Ч
тобы найти скорость надо путь поделить на время, следовательно, 6/х км/ч – намеченная скорость. х – 0,5 ч – время, затраченное фактически, 6/(х – 0,5) км/ч – фактическая скорость. По условию задачи известно, что пешеход увеличил скорость на
1 км/ч.
Получаем уравнение: 6/(х – 0,5) – 6/х = 1.
Если х≠0,5 и х≠0, то 6х – 6х + 3 = х2 – 0,5х
2х2 – х – 6 = 0,
D=1+48=49,
 =
=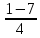 =-1,5
=-1,5  =
=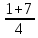 =2.
=2.Так как время – положительное число, то – 1,5 не подходит. Намеченное время – 2 часа, а скорость, с которой шел пешеход – 6 : 2 + 1 = 4 (км/ч).
Ответ: 4 км/ч.
Второй способ.
Пусть х км/ч – намеченная скорость, тогда 6/х ч – намеченное время. х + 1 км/ч – фактическая скорость, 6/(х+1) ч – фактическое время. По условию задачи известно, что пешеход затратил времени на ½ часа меньше, чем планировал. Получаем уравнение: 6/х – 6/(х+1) = ½.
Если х ≠ 0, х ≠ 1, то 12х + 12 – 12х = х2 + х,
х2 + х – 12 = 0,
D=1+48=49,
 =
=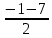 =-4,
=-4,  =
=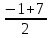 =3.
=3.Так как скорость – положительное число, то – 4 не подходит, значит, намеченная скорость 3 км/ч, а скорость движения пешехода 3 + 1 = 4 (км/ч).
Ответ: 4 км/ч.
Задача № 2. (Самостоятельно, с оказанием дифференцированной помощи)
Велосипедист проехал с постоянной скоростью 40 км от пункта А до пункта В. Возвращаясь обратно со скоростью, на 10 км/ч меньшей первоначальной, он затратил на 20 мин больше, чем на путь от А до В. Найдите первоначальную скорость велосипедиста.
Проверим решение:
Первый способ
Пусть х км/ч – скорость велосипедиста при движении из пункта А в пункт В, тогда время движения – 40/х ч. На обратном пути он ехал со скоростью (х – 10) км/ч и затратил 40/(х - 10) ч. По условию задачи известно, что на обратный путь велосипедист затратил больше на 20 мин или на 1/3 часа. Получаем уравнение: 40/(х - 10) – 40/х = 1/3.
Если х ≠ 0, х ≠ 10, то 120х – 120х + 1200 = х2 – 10х,
х2 – 10х – 1200 = 0,
D=100+4800=4900,
 =
=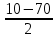 =-30,
=-30,  =
=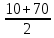 =40.
=40. = - 30 - условию задачи не удовлетворяет. Значит первоначальная скорость велосипедиста –
= - 30 - условию задачи не удовлетворяет. Значит первоначальная скорость велосипедиста –40 км/ч.
Ответ: 40 км/ч.
Второй способ
Пусть х ч – время, затраченное велосипедистом на путь от А до В, тогда его скорость 40/х км/ч. Время, затраченное на обратный путь (х + 1/3) ч, а скорость – 40/(х + 1/3) км/ч. По условию задачи известно, что обратно велосипедист ехал со скоростью, на 10 км/ч меньшей первоначальной. Получаем уравнение: 40/х - 40/(х + 1/3) = 10.
Если х ≠ 0 и х ≠ 1/3, то 40(х + 1/3) – 40х = 10х(х + 1/3),
3х2 + х – 4 = 0,
D=1+48=49,
 =
=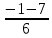 =-
=-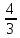 ,
,  =
=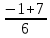 =1.
=1.