= - 4/3 –условию задачи не удовлетворяет. Значит, на путь от А до В был затрачен 1 час и первоначальная скорость велосипедиста 40 км/ч.

Ответ: 40 км/ч.
6. Подведение итогов урока.

- Какие задачи решали на уроке?

- Что нового вы узнали на уроке?

- Какие затруднения у вас возникли?

---

- Расскажите этапы решения задачи с помощью уравнения.

Отметить наиболее активных учеников. Выставить оценки.
7. Задание на дом. №565,№574, на повторение №578. Подготовить выступление трем учащимся на тему «История квадратных уравнений в Индии», «Квадратные уравнения в Древнем Вавилоне», «Квадратные уравнения в Европе в XIII – XVIIвв».

И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».

Поблагодарить учащихся за плодотворный урок.

Урок № 3

Тема урока: «Решение задач с помощью квадратных уравнений»

Цель урока:

- закреплять навыки решения задач с помощью квадратных уравнений;

- развивать логическое мышление учащихся.

Задачи урока: Проверить насколько дети научились составлять уравнение по условию задачи, определять тип текстовой задачи, знать особенности алгоритма её решения.

Тип урока: Урок закрепления нового материала. (В форме беседы)

Формы работы учащихся на уроке: Индивидуальная, коллективная.

Описание необходимого технического оборудования для проведения урока: Компьютер учителя, интерактивная доска.

Структура и ход проведения урока:

1.Сообщение темы и цели урока.

2. Путешествие в историю квадратных уравнений.

3.Творческое задание на дом.

4.Подведение итогов.

Ход урока:

1.Сообщение темы и цели урока.

Здравствуйте, ребята! Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Сегодня на уроке мы с вами отправимся в путешествие, в мир квадратных уравнений. Закрепим навыки решения квадратных уравнений и углубим знания, путем рассмотрения различных нестандартных задач.
2.Путешествие в историю квадратных уравнений.

К доске выходит ученик с сообщением «Квадратные уравнения в Индии»:

А знаете ли вы, что первое упоминание о задачах на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный

---

, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой форме: ах² + bх = с, а > 0. В этом уравнении коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Давайте решим одну из задач знаменитого индийского математика XII в. Бхаскары:

Обезьянок резвых стая,

Всласть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавлялась.

А двенадцать по лианам...

Стали прыгать, повисая...

Сколько ж было обезьянок,

Вы скажите, в этой стае?

Все вместе разбираем задачу, один ученик у доски.

Решение: Нам необходимо узнать сколь было всего обезьян? Значит, х обозначим количество обезьян. По условию восьмая часть забавлялась на поляне, значит, берем восьмую часть от общего количества обезьян - это будет 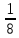х, да еще в квадрате 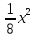. К этому количеству добавим еще, 12 обезьян, которые прыгают по лианам. Получим следующее уравнение: 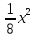+12=х.

Решим это уравнение:

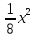+12=х,

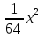-х+12=0,

D=1-4× 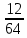= 0,25;

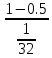= =16, = =48.

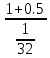=16, =48.

Два корня удовлетворяют условию задачи. Поэтому в стае могло быть 16 или 48 обезьян.

Ответ: 16 или 48 обезьян.

Учитель предлагает решить еще одну старинную задачу.

Задача: Квадрат пятой части обезьян, уменьшенной на 3, спрятался в гроте. Одна обезьяна, влезшая на дерево, была видна. Сколько было обезьян?

---

К доске приглашается ученик. Рассуждения над задачей ведется всем классом.

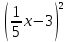Решение: В задаче надо найти, сколько было всего обезьян? Неизвестную величину обозначим х, тогда пятая часть от всего количества обезьян будет равна х. Это количество обезьян уменьшаем на 3, возводим в квадрат и добавляем 1 обезьяну. Получаем уравнение: +1=3.

Решим это уравнение:

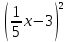+1=3,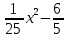

х+9+1=х,

,

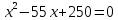D= 3025-1000=2025,

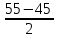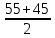= =5, = =50.

Находим корни квадратного уравнения: =5 – не подходит, т.к. если подставить значение 5 в исходное уравнение, то получим х-3=-2, -2 меньше нуля. Значит, условию задачи удовлетворяет второй корень =50.

Ответ: 50 обезьян.

Выходит следующий ученик с выступление «Квадратные уравнения в Древнем Вавилоне». Квадратные уравнения умели решать вавилоняне около 2000 лет до н. э. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных квадратных уравнений, и полные квадратные уравнения.

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратных уравнений. В Древнем Вавилоне образованные люди (это были жрецы и чиновники) умели решать задачи на определение длины и ширины прямоугольника по площади и периметру. Давайте мы побудим людьми Древнего Вавилона и решим пару задач.

---

Задача №1

Найдите стороны прямоугольника, длина которого на 4 см больше ширины, а площадь равна 60 .

Решение: Пусть х см ширина прямоугольника, тогда длина прямоугольника (х+4) см. По условию задачи площадь прямоугольника равна 60 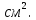Составим и решим уравнение:

х(х+4)=60,

+4х-60=0,

D=16+4×60=16+240=256,

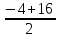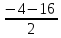= =6, = =-10.

Корень равный -10 условию задачи не удовлетворяет, т.к. ширина не может быть отрицательным числом. Следовательно, ширина равна 6м, а длина равна х+4=6+4=10м.

Ответ: 6м, 10 м.

Задача №2

Периметр прямоугольника 62 м. Найдите его стороны, если площадь прямоугольника равна

210

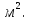
Решение: Пусть х м ширина прямоугольника, тогда у м длина прямоугольника. По условию периметр прямоугольника равен 62 м. Вспомним, формулу периметра прямоугольника получим: (х+у)×2=62. По условию знаем, что площадь прямоугольника равна 210 . Получаем х×у=210. Получаем два уравнения:

(х+у)×2=62, (1)

х×у=210. (2)

В уравнении (1) разделим обе части на 2.

х+у=31,

Выразим переменную х через у.

х=31-у,

Подставим во второе уравнение.

(31-у)×у=210,

Раскроем скобки.

31у- 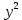=210,

Приведем к виду квадратного уравнения.

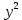- +31у-210=0, умножим на -1.

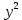-31у+210=0,

D=961-840=121.

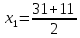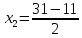=21, =10.

Корни подходят по условию задачи. Значит 21 м ширина прямоугольника, а 10 м его длина.

Ответ: 21м, 10м.

Небольшая разминка. Решите устно следующие уравнения. Задание на интерактивной доске.

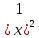=9,

(Ответ: -3; 3)

2) 3

---

Смотрите также файлы

• Анализ урока Задание. Посмотрите видеоурок (по своему профилю) (закрепите активную ссылку).docx

• Оптические и лазерные системы Индивидуальное расчетное задание.docx

• Расчёт инвестиционного проекта.docx

• Цель занятия закрепление знаний об основных формах работы детского сада с неорганизованными детьми, формирование умения применять полученные знания на практике Задание 1.docx

• Структура Периодической таблицы.docx