Файл: Тема урока Решение задач с помощью квадратных уравнений Класс 8 Тема урока Решение задач с помощью квадратных уравнений. Цели урока Образовательные формирование познавательных ууд.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 40
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=300,
(Ответ: -10; 10)
3) 2
-8=0,
(Ответ: -2; 2)
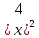-3x=0,
(Ответ: 0; 3)
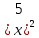+6x+9=0,
(Ответ: -3)
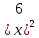-10x+25=0,
(Ответ:5)
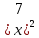+16x+63=0,
(Ответ: -9, -7)
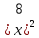-3x+2=0.
(Ответ: 2, 1).
К доске выходит следующий ученик с сообщением на тему «Квадратные уравнения в Европе в XIII – XVIIвв».
Формы решения квадратных уравнений по образцу ал-Хорезми в Европе были в первые изложены в «Книге абаха», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраический примеры решения задач и первый в Европе подошёл к введениям отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абаха» переходили почти во все европейские учебники XVI – XVII вв. и частично XVIII в. Общее правило решений квадратных уравнений, приведенных к единому каноническому виду:
+ bx=c
при всевозможных комбинациях знаков и коэффициентов b,c, было сформировано в Европе в 1544г. М. Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские учёные Тарталья, Кардано, Бомбелли среди первых в XVIIв. учитывают, помимо положительных и отрицательные корни. Лишь в XVIIв. благодаря трудам Жиррара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.
У доски решаем следующие задачи.
Задача №1
Изготовить прямоугольник, если известно, что одна из сторон на 14 см больше другой, а диагональ прямоугольника равна 34 см.
Решение: Пусть х см наименьшая из сторон прямоугольника, тогда наибольшая сторона равна (х+14) см. Проводя диагональ, мы делим прямоугольник на два треугольника. Диагональ в прямоугольном треугольнике играет роль гипотенузы. Для правильного составления уравнения мы должны вспомнить теорему Пифагора, и свойство противоположных сторон прямоугольника. Получаем уравнение:
+
=
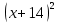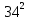
Решаем уравнение, раскрыв скобки:
+ +28х+196=1156,
2 +28х+196-1156=0,
2 +28х-960=0, сократим квадратное уравнение на 2
+14х-480=0,
D=196+1920=21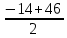16,
=
=16, 
=
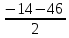=-30 не подходит.
=16 см – наименьшая из сторон прямоугольника.
х+14=16+14=30,
=30 см – наибольшая из сторон прямоугольника.
Ответ: 16 см и 30 см.
Задача №2
Изготовить прямоугольный треугольник, если один из катетов на 3 см меньше гипотенузы, а другой на 6 см меньше гипотенузы.
Решение: Пусть х см гипотенуза прямоугольного треугольника, тогда (х-3)см один из катетов, а другой (х-6)см. Вспомним теорему Пифагора! Квадрат гипотенузы, равен сумме квадратов катетов. Получаем уравнение: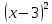
+
= .
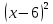Решим уравнение, раскрыв скобки:
-6х+9+ -12х+36- =0,
-18х+45=0,
D=324-4×45=144,
=
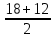
=15, =
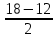=3.
=15, =3 – второй корень условию задачи не удовлетворяет.
15см – гипотенуза прямоугольного треугольника.
15-3=12 см – один катет прямоугольного треугольника.
15-6=9 см – второй катет прямоугольного треугольника.
Ответ: катеты 12 см и 9 см, гипотенуза 15 см.
Задача №3
Произведение двух последовательных целых чисел больше их суммы на 109. Найдите эти числа.
Решение: Пусть одно из чисел мы обозначим х, следовательно, последующее число на 1 больше – (х+1). Произведение двух чисел равно – х(х+1), а сумма – (х+х+1). По условию задачи произведение этих чисел больше их суммы на 109. Получаем уравнение: х(х+1)-(х+х+1)=109.
Раскроем скобки: +х-х-х-1=109,
-х-1=109,
-х-110=0,
D=1+440=441,
=
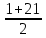=11, =
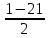=-10.
Если 11 одно из целых чисел, то последующее 11+1=12.
Если -10 одно из целых чисел, то последующее -10+1=-9.
Ответ: -10 и -9, 11 и 12.
3.Творческое задание на дом.
Ученикам предлагается самостоятельно придумать три задачи, решаемые с помощью квадратных уравнений.
4. Подведение итогов.
1. Поблагодарить учеников подготовивших сообщения. ( Выставить оценки)
2. Отметить наиболее активных участников урока. Поставить отметку тем, кто самостоятельно составил уравнения.
3. Попросить учащихся самостоятельно себя оценить, продолжив предложения
а) Сегодня на уроке я …
б) Сегодня на уроке я смог (или не смог) самостоятельно составить к задаче …… и его решить.
Сделать вывод! Поблагодарить за интересный урок!
Приложение
Урок №1
Карточка №1
1 Вариант
1. Уравнение вида
, где a, b, c - заданные числа, a
0, x - переменная,
называется...
2. Полное квадратное уравнение не имеет корней, если D ...
3. Уравнение вида
называется...
4. Квадратное уравнение имеет два корня, если
...
5. Дано уравнение
. D =...
Карточка №2
2 Вариант
1. Если квадратное уравнение, то a... коэффициент, с...
2. Уравнение x² = a, где a < 0, не имеет...
3. Полное квадратное уравнение имеет единственный корень, если ...
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют ... квадратным
уравнением.
5. Дано уравнение x²- 6x + 8 = 0. D =...
Урок №2
Карточка № 1.
1.Запиши общий вид квадратного уравнения.
2.Запиши формулу корней квадратного уравнения.
3.Чему равны коэффициенты а, в, с уравнения х2 – 4х – 3 = 0?
4.Реши уравнения: а) 3х2 + 2 х – 1 = 0; б) 2х 2+ 7х – 4 = 0; в) х2 – 7х +12 = 0.
Карточка № 2
1.Запишите формулу дискриминанта квадратного уравнения.
2.Сколько корней имеет уравнение, если D > 0? D < 0? D = 0?
3. Реши уравнения: а) 5х2 + 8х – 4 = 0; б) х2 – 6х + 11 = 0; в) 7х2 + 6х – 1 = 0
Карточка №1
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 156. Найдите эти числа.
Карточка № 2
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 210. Найдите эти числа.
Урок №3
=9,
2) 3 =300,
3) 2 -8=0,
-3x=0,
+6x+9=0,
-10x+25=0,
+16x+63=0,
-3x+2=0.
Приложение
Карточка основного понятия
Предмет: Алгебра
Тема: «Решение задач с помощью квадратных уравнений»
Понятие: Квадратное уравнение, дискриминант, корни квадратного уравнения.
Разработчик: Тишина Инна Анатольевна
(Ответ: -10; 10)
3) 2
-8=0,(Ответ: -2; 2)
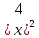-3x=0,(Ответ: 0; 3)
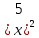+6x+9=0,(Ответ: -3)
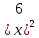-10x+25=0,(Ответ:5)
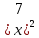+16x+63=0,(Ответ: -9, -7)
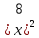-3x+2=0.(Ответ: 2, 1).
К доске выходит следующий ученик с сообщением на тему «Квадратные уравнения в Европе в XIII – XVIIвв».
Формы решения квадратных уравнений по образцу ал-Хорезми в Европе были в первые изложены в «Книге абаха», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраический примеры решения задач и первый в Европе подошёл к введениям отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абаха» переходили почти во все европейские учебники XVI – XVII вв. и частично XVIII в. Общее правило решений квадратных уравнений, приведенных к единому каноническому виду:
+ bx=cпри всевозможных комбинациях знаков и коэффициентов b,c, было сформировано в Европе в 1544г. М. Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские учёные Тарталья, Кардано, Бомбелли среди первых в XVIIв. учитывают, помимо положительных и отрицательные корни. Лишь в XVIIв. благодаря трудам Жиррара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.
У доски решаем следующие задачи.
Задача №1
Изготовить прямоугольник, если известно, что одна из сторон на 14 см больше другой, а диагональ прямоугольника равна 34 см.
Решение: Пусть х см наименьшая из сторон прямоугольника, тогда наибольшая сторона равна (х+14) см. Проводя диагональ, мы делим прямоугольник на два треугольника. Диагональ в прямоугольном треугольнике играет роль гипотенузы. Для правильного составления уравнения мы должны вспомнить теорему Пифагора, и свойство противоположных сторон прямоугольника. Получаем уравнение:
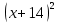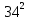
+ = Решаем уравнение, раскрыв скобки:
+ +28х+196=1156,2
+28х+196-1156=0,2
+28х-960=0, сократим квадратное уравнение на 2 +14х-480=0,D=196+1920=21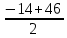16,
= =16, = =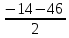-30 не подходит. =16 см – наименьшая из сторон прямоугольника.х+14=16+14=30,
=30 см – наибольшая из сторон прямоугольника.Ответ: 16 см и 30 см.
Задача №2
Изготовить прямоугольный треугольник, если один из катетов на 3 см меньше гипотенузы, а другой на 6 см меньше гипотенузы.
Решение: Пусть х см гипотенуза прямоугольного треугольника, тогда (х-3)см один из катетов, а другой (х-6)см. Вспомним теорему Пифагора! Квадрат гипотенузы, равен сумме квадратов катетов. Получаем уравнение:
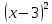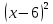+ = .Решим уравнение, раскрыв скобки:
-6х+9+ -12х+36- =0, -18х+45=0,D=324-4×45=144,
=
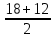
=15,
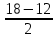= =3. =15, =3 – второй корень условию задачи не удовлетворяет.15см – гипотенуза прямоугольного треугольника.
15-3=12 см – один катет прямоугольного треугольника.
15-6=9 см – второй катет прямоугольного треугольника.
Ответ: катеты 12 см и 9 см, гипотенуза 15 см.
Задача №3
Произведение двух последовательных целых чисел больше их суммы на 109. Найдите эти числа.
Решение: Пусть одно из чисел мы обозначим х, следовательно, последующее число на 1 больше – (х+1). Произведение двух чисел равно – х(х+1), а сумма – (х+х+1). По условию задачи произведение этих чисел больше их суммы на 109. Получаем уравнение: х(х+1)-(х+х+1)=109.
Раскроем скобки:
+х-х-х-1=109, -х-1=109, -х-110=0,D=1+440=441,
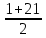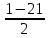= =11, = =-10.Если 11 одно из целых чисел, то последующее 11+1=12.
Если -10 одно из целых чисел, то последующее -10+1=-9.
Ответ: -10 и -9, 11 и 12.
3.Творческое задание на дом.
Ученикам предлагается самостоятельно придумать три задачи, решаемые с помощью квадратных уравнений.
4. Подведение итогов.
1. Поблагодарить учеников подготовивших сообщения. ( Выставить оценки)
2. Отметить наиболее активных участников урока. Поставить отметку тем, кто самостоятельно составил уравнения.
3. Попросить учащихся самостоятельно себя оценить, продолжив предложения
а) Сегодня на уроке я …
б) Сегодня на уроке я смог (или не смог) самостоятельно составить к задаче …… и его решить.
Сделать вывод! Поблагодарить за интересный урок!
Приложение
Урок №1
Карточка №1
1 Вариант
1. Уравнение вида
, где a, b, c - заданные числа, a 0, x - переменная, называется...
2. Полное квадратное уравнение не имеет корней, если D ...
3. Уравнение вида
называется...4. Квадратное уравнение имеет два корня, если
...5. Дано уравнение
. D =...Карточка №2
2 Вариант
1. Если
квадратное уравнение, то a... коэффициент, с...2. Уравнение x² = a, где a < 0, не имеет...
3. Полное квадратное уравнение имеет единственный корень, если
...4. Уравнение вида ax² + c = 0, где a
0, c 0, называют ... квадратным уравнением.
5. Дано уравнение x²- 6x + 8 = 0. D =...
Урок №2
Карточка № 1.
1.Запиши общий вид квадратного уравнения.
2.Запиши формулу корней квадратного уравнения.
3.Чему равны коэффициенты а, в, с уравнения х2 – 4х – 3 = 0?
4.Реши уравнения: а) 3х2 + 2 х – 1 = 0; б) 2х 2+ 7х – 4 = 0; в) х2 – 7х +12 = 0.
Карточка № 2
1.Запишите формулу дискриминанта квадратного уравнения.
2.Сколько корней имеет уравнение, если D > 0? D < 0? D = 0?
3. Реши уравнения: а) 5х2 + 8х – 4 = 0; б) х2 – 6х + 11 = 0; в) 7х2 + 6х – 1 = 0
Карточка №1
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 156. Найдите эти числа.
Карточка № 2
Произведение двух натуральных чисел, одно из которых на 1 больше другого, равно 210. Найдите эти числа.
Урок №3
=9,
2) 3
=300,3) 2
-8=0, -3x=0, +6x+9=0, -10x+25=0, +16x+63=0, -3x+2=0.Приложение
Карточка основного понятия
Предмет: Алгебра
Тема: «Решение задач с помощью квадратных уравнений»
Понятие: Квадратное уравнение, дискриминант, корни квадратного уравнения.
Разработчик: Тишина Инна Анатольевна
| № п/п | Вопрос | Ответ |
| 1 | Что такое квадратное уравнение? | Это уравнение вида, а + bx + с = 0, где х неизвестное, а, b, с — некоторые числа, причем а≠0 |
| 2 | Из чего состоит квадратное уравнение? Какие бывают квадратные уравнения? Как решать квадратные уравнения? | Из некоторых чисел, которые называются коэффициентами квадратного уравнения. а - называется первым коэффициентом; b -называется вторым коэффициентом; с - свободным членом. Если в квадратном уравнении коэффициенты и не равны нулю, то уравнение называется полным квадратным уравнением. Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Неполным квадратным уравнением называется такое, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю. Сначала находится величина, называемая дискриминантом: D= 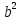 -4асПосле того, как дискриминант вычислен, возможны три варианта. 1) Если дискриминант D больше нуля, то уравнение имеет два разных корня - и .В этом случае корни вычисляются по формулам: = 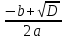, = 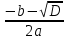.2) Если дискриминант D равен нулю, уравнение имеет один корень х, который вычисляется по формуле: х= 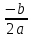 3) Если же дискриминант D меньше нуля, то уравнение не имеет корней (и именно это нужно написать в ответе). |
| 3 | Какие преимущества в жизни получит ученик, понимая (хорошо зная), что такое квадратное уравнение и как его решить? | - При выборе профессии связанной с математикой, например архитектор, экономист, инженер и т.д. - Если свою жизнь свяжет с научной деятельностью. |
| 4 | Какие вероятные проблемы (негативные последствия) могут наступить, если ученик не знает (не имеет представления, слабо знает), что называем квадратным уравнением и способы его решения? | Квадратные уравнения очень актуальны. Одна из основных тем ЕМЭ – это квадратные уравнения. Одной из основных тем, проверяемых на экзамене по математике, является тема «Квадратные уравнения». Данная тема изучается в 8 классе, а на повторение данной темы в 9 классе отводится один час. Поэтому знания квадратных уравнений помогут сдать экзамен по алгебре на более высокий бал. Также квадратные уравнения используются в физике и в химии для решения задач в 10 и 11 класса, знание данной темы поможет при сдаче ЕГЭ по этим предметам. |