Файл: Лабораторная работа 1к определение скорости пули при помощи баллистического маятника содержание Введение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 405
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
вне проводника компенсируются электрическими полями неподвижных зарядов проводника противоположного знака.
Силовую характеристику магнитного поля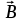 называют вектором магнитной индукции, хотя по аналогии с электрическим полем следовало бы назвать напряженностью магнитного поля. Но исторически сложилось так, что напряженностью
называют вектором магнитной индукции, хотя по аналогии с электрическим полем следовало бы назвать напряженностью магнитного поля. Но исторически сложилось так, что напряженностью 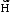 называют вспомогательную характеристику магнитного поля.
называют вспомогательную характеристику магнитного поля.
2. Закон Био-Савара-Лапласа
Экспериментально магнитное поле, создаваемое током, изучали французкие ученые Ж. Био и Ф. Савар, результаты этих исследований математически оформил их соотечественник П. Лаплас.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: поле системы токов равно сумме полей, создаваемых каждым током. Вектор магнитной индукции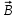 равен векторной сумме полей
равен векторной сумме полей 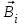 , создаваемых каждым источником поля в отдельности:
, создаваемых каждым источником поля в отдельности:
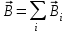 ,
,
где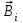 – вектор магнитной индукции поля, созданного i-ым током.
– вектор магнитной индукции поля, созданного i-ым током.
Для того, чтобы можно было определить магнитное поле любой системы токов, достаточно найти выражение для вектора магнитной индукции поля, создаваемого элементом тока.
Под элементом тока понимают элемент проводника с током с учетом его направления, т.е. элемент тока – это вектор, равный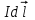 (см. рис. 1).
(см. рис. 1).
На основании опытов Ж. Био и Ф. Савара П. Лапласом установлено, что вектор магнитной индукции поля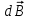 в точке
в точке 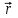 , созданного элементом тока Idl, равен (см. рис. 1):
, созданного элементом тока Idl, равен (см. рис. 1):
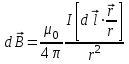 . (1)
. (1)
Формула (1) является математическим выражением закона Био-Савара-Лапласа.
Направление определяется направлением векторного произведения. Оно перпендикулярно плоскости, в которой лежат
определяется направлением векторного произведения. Оно перпендикулярно плоскости, в которой лежат 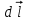 и
и  и определяется правилом правого винта:
и определяется правилом правого винта:
а) винт установить перпендикулярно плоскости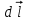 и
и  ;
;
б) вращать от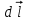 к
к  ;
;
в) поступательное движение винта покажет направление – вектора магнитной индукции, созданного элементом
– вектора магнитной индукции, созданного элементом 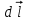 проводника с током I.
проводника с током I.
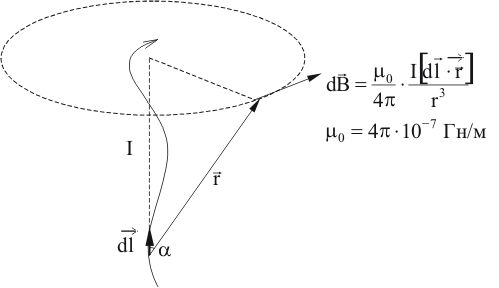
Рис.1
Результирующее поле, созданное проводником, находится по принципу суперпозиции магнитных полей:
Модуль вектора :
:
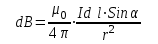 . (2)
. (2)
Единица измерения магнитной индукции – «тесла» (Тл).
Магнитное поле графически изображается, как и электрическое, с помощью линий магнитной индукции (магнитных силовых линий).
Линии магнитной индукции:
1) замкнуты, так как в природе нет магнитных зарядов;
2) вектор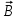 направлен по касательной к линии магнитной индукции;
направлен по касательной к линии магнитной индукции;
3) густота линий магнитной индукции пропорциональна модулю векто-
ра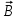 .
.
3. Применение закона Био-Савара-Лапласа для расчета магнитного поля в центре кольца с током
Чтобы найти поле в центре кольца с током, мысленно разобьем его на множество элементов тока (см. рис. 2а).
Каждый элемент тока, согласно закону Био-Савара-Лапласа, создает магнитное поле с индукцией
 , определяемой формулой (1).
, определяемой формулой (1).
Прежде всего проверим, как направлены векторы , создаваемые каждым элементом тока. Пользуясь приведенным выше правилом правого винта для определения направления
, создаваемые каждым элементом тока. Пользуясь приведенным выше правилом правого винта для определения направления  , легко убедиться, что в центре кольца все векторы
, легко убедиться, что в центре кольца все векторы  направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму
направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму  можно заменить арифметической, и для магнитной индукции в центре кольца получаем на основе (2) выражение:
можно заменить арифметической, и для магнитной индукции в центре кольца получаем на основе (2) выражение:
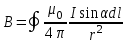 .
.
Р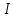
ис. 2а
И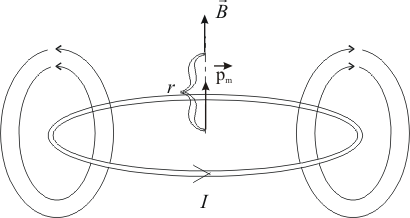 з геометрии задачи видно, что
з геометрии задачи видно, что 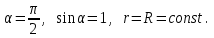
Рис. 2б
Вынося из-под знака интеграла постоянные величины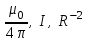 , получаем:
, получаем:
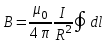 .
.
Интеграл по окружности равен ее длине:
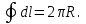
Таким образом, магнитная индукция в центре кольца равна:
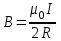 . (3)
. (3)
Вектор магнитной индукции направлен перпендикулярно плоскости кольца, направление вектора определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора
определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора  .
.
Магнитный диполь
Используя более сложные математические методы, можно на основе закона Био-Савара-Лапласа рассчитать магнитную индукцию, создаваемую кольцом с током в любой точке пространства. При этом оказалось, что картина магнитного поля вне кольца с током полностью аналогична электрическому полю, создаваемому электрическим диполем .
Магнитное поле кольца, по которому течет ток, вне кольца можно рассматривать как поле магнитного диполя.
Более того, магнитное поле любого контура с током или поле движущихся зарядов, локализованных в ограниченной области пространства, на больших расстояниях приближенно можно рассматривать как магнитное поле диполя. Такой диполь характеризуется дипольным магнитным моментом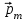 . Модуль дипольного магнитного момента:
. Модуль дипольного магнитного момента:
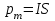 , (4)
, (4)
где S – площадь контура с током.
Направление вектора магнитного момента контура с током совпадает с направлением положительной нормали к контуру (см. рис. 2б).
Так как магнитные свойства веществ (магнитной стрелки) объясняются внутриатомными движениями электрических зарядов, то магнитную стрелку можно характеризовать вектором магнитного момента .
.
Ф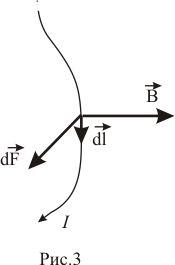 ранцузский ученый Ампер установил, что на элемент тока в магнитном поле действует сила
ранцузский ученый Ампер установил, что на элемент тока в магнитном поле действует сила
 , (5)
, (5)
где I – сила тока.
Формула (5) является математическим выражением закона Ампера, ее иллюстрирует рис. 3.
Модуль вектора равен
равен 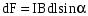 (6)
(6)
Если векторы и
и  взаимно перпендикулярны, можно использовать более удобное правило – правило левой руки: левую руку располагают так, чтобы силовые линии вектора магнитной индукции входили в ладонь, а четыре пальца были направлены по току, тогда отогнутый большой палец покажет направление силы, действующий на проводник с током.
взаимно перпендикулярны, можно использовать более удобное правило – правило левой руки: левую руку располагают так, чтобы силовые линии вектора магнитной индукции входили в ладонь, а четыре пальца были направлены по току, тогда отогнутый большой палец покажет направление силы, действующий на проводник с током.
Силу, действующую на проводник с током в магнитном поле называют силой Ампера.
Для того, чтобы найти силу Ампера, действующую на проводник сложной формы или больших размеров, нужно разбить проводник на элементы тока и затем найти
векторную сумму сил, действующих на элементы тока.
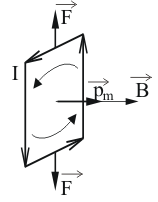
4.Рамка с током в магнитном поле
Р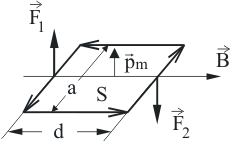 ассмотрим прямоугольную рамку с током, расположенную так, что магнитные силовые линии лежат в плоскости рамки (см. рис. 4).
ассмотрим прямоугольную рамку с током, расположенную так, что магнитные силовые линии лежат в плоскости рамки (см. рис. 4).
На каждую из сторон рамки действует согласно формуле (5) сила Ампера.
Силы, действующие на стороны рамки параллельные , равны нулю;
, равны нулю;
Рис.4 на стороны перпендикулярные , равны по величине и противоположны по направлению.
, равны по величине и противоположны по направлению.
Модуль сил (см. формулу(6), при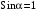 ), равен:
), равен:
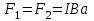 .
.
Механические моменты сил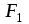 и
и 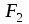 относительно оси, лежащей в плоскости рамки и проходящей через ее центр, равны по модулю и одинаково направлены. Суммарный момент сил равен по модулю:
относительно оси, лежащей в плоскости рамки и проходящей через ее центр, равны по модулю и одинаково направлены. Суммарный момент сил равен по модулю:
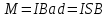 .
.
По определению модуля магнитного момента (4): IS=pm, значит, если вектор магнитной индукции лежит в плоскости рамки, то на рамку с током действует механический момент сил
лежит в плоскости рамки, то на рамку с током действует механический момент сил 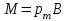 , стремящийся повернуть рамку так, чтобы магнитный момент
, стремящийся повернуть рамку так, чтобы магнитный момент 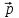 был параллелен вектору
был параллелен вектору .
.
Аналогично можно рассмотреть случай, когда вектор магнитной индукции перпендикулярен плоскости рамки.
В этом случае механический момент равен нулю,
так как плечи всех сил относительно оси вращения равны нулю. Суммарная сила, действующая на рамку с током, также равна нулю (см. рис. 5).
В промежуточном случае, когда вектор и нормаль к рамке образуют угол , вектор
и нормаль к рамке образуют угол , вектор 
Силовую характеристику магнитного поля
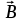 называют вектором магнитной индукции, хотя по аналогии с электрическим полем следовало бы назвать напряженностью магнитного поля. Но исторически сложилось так, что напряженностью
называют вектором магнитной индукции, хотя по аналогии с электрическим полем следовало бы назвать напряженностью магнитного поля. Но исторически сложилось так, что напряженностью 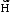 называют вспомогательную характеристику магнитного поля.
называют вспомогательную характеристику магнитного поля.2. Закон Био-Савара-Лапласа
Экспериментально магнитное поле, создаваемое током, изучали французкие ученые Ж. Био и Ф. Савар, результаты этих исследований математически оформил их соотечественник П. Лаплас.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: поле системы токов равно сумме полей, создаваемых каждым током. Вектор магнитной индукции
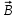 равен векторной сумме полей
равен векторной сумме полей 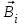 , создаваемых каждым источником поля в отдельности:
, создаваемых каждым источником поля в отдельности: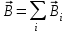 ,
,где
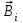 – вектор магнитной индукции поля, созданного i-ым током.
– вектор магнитной индукции поля, созданного i-ым током.Для того, чтобы можно было определить магнитное поле любой системы токов, достаточно найти выражение для вектора магнитной индукции поля, создаваемого элементом тока.
Под элементом тока понимают элемент проводника с током с учетом его направления, т.е. элемент тока – это вектор, равный
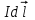 (см. рис. 1).
(см. рис. 1).На основании опытов Ж. Био и Ф. Савара П. Лапласом установлено, что вектор магнитной индукции поля
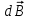 в точке
в точке 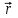 , созданного элементом тока Idl, равен (см. рис. 1):
, созданного элементом тока Idl, равен (см. рис. 1):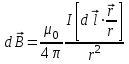 . (1)
. (1)Формула (1) является математическим выражением закона Био-Савара-Лапласа.
Направление
 определяется направлением векторного произведения. Оно перпендикулярно плоскости, в которой лежат
определяется направлением векторного произведения. Оно перпендикулярно плоскости, в которой лежат 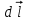 и
и  и определяется правилом правого винта:
и определяется правилом правого винта:а) винт установить перпендикулярно плоскости
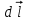 и
и  ;
;б) вращать от
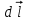 к
к  ;
; в) поступательное движение винта покажет направление
 – вектора магнитной индукции, созданного элементом
– вектора магнитной индукции, созданного элементом 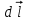 проводника с током I.
проводника с током I.
Рис.1
Результирующее поле, созданное проводником, находится по принципу суперпозиции магнитных полей:
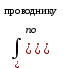
Модуль вектора
 :
: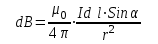 . (2)
. (2)Единица измерения магнитной индукции – «тесла» (Тл).
Магнитное поле графически изображается, как и электрическое, с помощью линий магнитной индукции (магнитных силовых линий).
Линии магнитной индукции:
1) замкнуты, так как в природе нет магнитных зарядов;
2) вектор
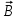 направлен по касательной к линии магнитной индукции;
направлен по касательной к линии магнитной индукции;3) густота линий магнитной индукции пропорциональна модулю векто-
ра
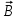 .
.3. Применение закона Био-Савара-Лапласа для расчета магнитного поля в центре кольца с током
Чтобы найти поле в центре кольца с током, мысленно разобьем его на множество элементов тока (см. рис. 2а).
Каждый элемент тока, согласно закону Био-Савара-Лапласа, создает магнитное поле с индукцией
 , определяемой формулой (1).
, определяемой формулой (1).Прежде всего проверим, как направлены векторы
 , создаваемые каждым элементом тока. Пользуясь приведенным выше правилом правого винта для определения направления
, создаваемые каждым элементом тока. Пользуясь приведенным выше правилом правого винта для определения направления  , легко убедиться, что в центре кольца все векторы
, легко убедиться, что в центре кольца все векторы  направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму
направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму  можно заменить арифметической, и для магнитной индукции в центре кольца получаем на основе (2) выражение:
можно заменить арифметической, и для магнитной индукции в центре кольца получаем на основе (2) выражение: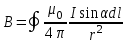 .
.Р
ис. 2а
И
 з геометрии задачи видно, что
з геометрии задачи видно, что 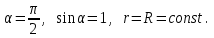
Рис. 2б
Вынося из-под знака интеграла постоянные величины
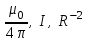 , получаем:
, получаем: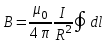 .
.Интеграл по окружности равен ее длине:
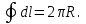
Таким образом, магнитная индукция в центре кольца равна:
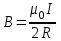 . (3)
. (3) Вектор магнитной индукции направлен перпендикулярно плоскости кольца, направление вектора
 определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора
определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора  .
. Магнитный диполь
Используя более сложные математические методы, можно на основе закона Био-Савара-Лапласа рассчитать магнитную индукцию, создаваемую кольцом с током в любой точке пространства. При этом оказалось, что картина магнитного поля вне кольца с током полностью аналогична электрическому полю, создаваемому электрическим диполем .
Магнитное поле кольца, по которому течет ток, вне кольца можно рассматривать как поле магнитного диполя.
Более того, магнитное поле любого контура с током или поле движущихся зарядов, локализованных в ограниченной области пространства, на больших расстояниях приближенно можно рассматривать как магнитное поле диполя. Такой диполь характеризуется дипольным магнитным моментом
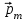 . Модуль дипольного магнитного момента:
. Модуль дипольного магнитного момента: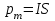 , (4)
, (4)где S – площадь контура с током.
Направление вектора магнитного момента контура с током совпадает с направлением положительной нормали к контуру (см. рис. 2б).
Так как магнитные свойства веществ (магнитной стрелки) объясняются внутриатомными движениями электрических зарядов, то магнитную стрелку можно характеризовать вектором магнитного момента
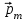 .
.3. Закон Ампера
Ф
 ранцузский ученый Ампер установил, что на элемент тока в магнитном поле действует сила
ранцузский ученый Ампер установил, что на элемент тока в магнитном поле действует сила , (5)
, (5)где I – сила тока.
Формула (5) является математическим выражением закона Ампера, ее иллюстрирует рис. 3.
Модуль вектора
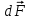 равен
равен 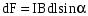 (6)
(6) Если векторы
 и
и  взаимно перпендикулярны, можно использовать более удобное правило – правило левой руки: левую руку располагают так, чтобы силовые линии вектора магнитной индукции входили в ладонь, а четыре пальца были направлены по току, тогда отогнутый большой палец покажет направление силы, действующий на проводник с током.
взаимно перпендикулярны, можно использовать более удобное правило – правило левой руки: левую руку располагают так, чтобы силовые линии вектора магнитной индукции входили в ладонь, а четыре пальца были направлены по току, тогда отогнутый большой палец покажет направление силы, действующий на проводник с током.Силу, действующую на проводник с током в магнитном поле называют силой Ампера.
Для того, чтобы найти силу Ампера, действующую на проводник сложной формы или больших размеров, нужно разбить проводник на элементы тока и затем найти
векторную сумму сил, действующих на элементы тока.
4.Рамка с током в магнитном поле
Р
 ассмотрим прямоугольную рамку с током, расположенную так, что магнитные силовые линии лежат в плоскости рамки (см. рис. 4).
ассмотрим прямоугольную рамку с током, расположенную так, что магнитные силовые линии лежат в плоскости рамки (см. рис. 4).На каждую из сторон рамки действует согласно формуле (5) сила Ампера.
Силы, действующие на стороны рамки параллельные
 , равны нулю;
, равны нулю; Рис.4 на стороны перпендикулярные
 , равны по величине и противоположны по направлению.
, равны по величине и противоположны по направлению.Модуль сил (см. формулу(6), при
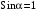 ), равен:
), равен: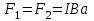 .
.Механические моменты сил
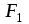 и
и 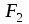 относительно оси, лежащей в плоскости рамки и проходящей через ее центр, равны по модулю и одинаково направлены. Суммарный момент сил равен по модулю:
относительно оси, лежащей в плоскости рамки и проходящей через ее центр, равны по модулю и одинаково направлены. Суммарный момент сил равен по модулю: 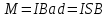 .
.По определению модуля магнитного момента (4): IS=pm, значит, если вектор магнитной индукции
 лежит в плоскости рамки, то на рамку с током действует механический момент сил
лежит в плоскости рамки, то на рамку с током действует механический момент сил 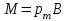 , стремящийся повернуть рамку так, чтобы магнитный момент
, стремящийся повернуть рамку так, чтобы магнитный момент 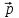 был параллелен вектору
был параллелен вектору .
.Аналогично можно рассмотреть случай, когда вектор магнитной индукции перпендикулярен плоскости рамки.

В этом случае механический момент равен нулю,
так как плечи всех сил относительно оси вращения равны нулю. Суммарная сила, действующая на рамку с током, также равна нулю (см. рис. 5).
В промежуточном случае, когда вектор
 и нормаль к рамке образуют угол , вектор
и нормаль к рамке образуют угол , вектор 