Файл: Лабораторная работа 1к определение скорости пули при помощи баллистического маятника содержание Введение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 395
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
#МЕТОД ИЗМЕРЕНИЙ.
Данная компьютерная программа моделирует натурную лабораторную работу «Определение скорости пули при помощи баллистического маятника».
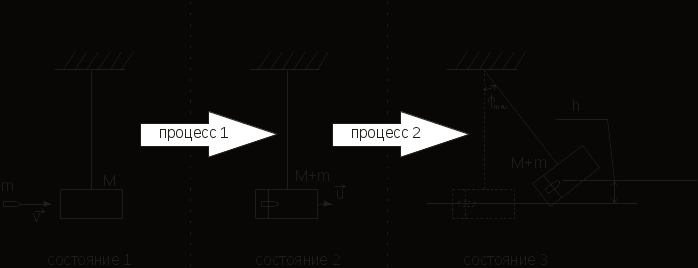
Баллистический маятник - это массивное тело, подвешенное на длинных нитях. В натурной лабораторной работе этим телом является полый цилиндр, заполненный пластилином. Обозначим массу этого цилиндра буквой М. В цилиндр стреляют из пружинного пистолета пулей массой m. Пуля, летящая со скоростью v, попадает в баллистический маятник и застревает в пластилине. Цилиндр маятника, висевший неподвижно, получает вследствие удара пули некоторый импульс и отклоняется от положения равновесия. Законы сохранения импульса и энергии позволяют связать скорость пули v с отклонением маятника и найти скорость пули по величине отклонения. На следующем рисунке изображена система «пуля-маятник» в трех важных для установления этой связи состояниях.
Состояние 1 - пуля вылетела из пистолета, но еще не долетела до мишени. Мишень неподвижна.
Состояние 2 - пуля попала в мишень, мишень вместе с пулей начали движение со скоростью u, отклонение маятника приблизительно равно нулю.
Состояние 3 - маятник отклонился на максимальный угол. Условно обозначены стрелками на рисунке два процесса перехода между этими состояниями.
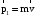
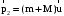

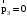
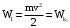
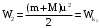
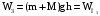
В процессе перехода системы из первого состояния во второе (процесс 1) сохраняется горизонтальная составляющая импульса системы, так как по горизонтали система замкнута (сопротивлением воздуха пренебрегаем). Таким образом, горизонтальная составляющая полного импульса системы до попадания пули в маятник
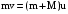 (2)
(2)Закон сохранения импульса связывает состояние 1 и состояние 2. Полная механическая энергия системы «пуля-маятник» в процессе 1 не сохраняет ся, так как при движении пули в пластилине действуют неконсервативные силы (силы трения пули о пластилин).
Убыль энергии равна выделившемуся в системе теплу (работе деформации):
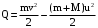 (3)
(3)В процессе 2 (перехода из второго состояние в третье) работу совершают только консервативные силы тяжести, поэтому к процессу 2 можно применить закон сохранения полной механической энергии:

где
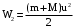 - полная механическая энергия системы «пуля-маятник» в состоянии 2;
- полная механическая энергия системы «пуля-маятник» в состоянии 2;Приравнивая
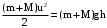

Эта формула дает связь между параметрами второго и третьего состояний. После сокращения на (m + М) и очевидных преобразований имеем:
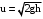
(4)
Таким образом, равенства (2) и (4) связывают между собой первое и третье состояние. Исключая из них промежуточный параметр u, получим:
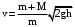 . (5)
. (5)Это и есть рабочая формула для определения скорости пули в лабораторной работе № 1-к.
Рабочую формулу для определения выделившейся теплоты
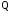 получим из формулы (3), подставив в нее v из формулы (5) и u из формулы (4):,
получим из формулы (3), подставив в нее v из формулы (5) и u из формулы (4):,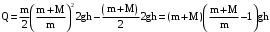
,
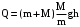 .
. Здесь, g = 9,81 м/с2 – ускорение свободного падения.
В процессе любого измерения за счёт различных воздействий, причины которых нам могут быть неизвестны, неизбежно появляются случайные ошибки.
Величину случайной погрешности можно свести к минимуму путём многократного повторения эксперимента при сохранении одних и тех же контролируемых нами условий. Затем проводится математическая обработка полученных результатов: а) находится среднее арифметическое значение измеренной величины;
б) её среднеквадратичная ошибка
 ;
;в) по известному числу измерений n и заданной надёжности в из таблицы находится
коэффициент Стьюдента t(в,n);
г) затем определяется доверительный интервал.
Среднее значение скорости пули рассчитываем по формуле:
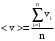 , (7)
, (7)
где n – число экспериментов, выполненных при одинаковых значениях начальных параметров, 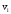 - значение скорости, рассчитанное для каждого такого эксперимента.
- значение скорости, рассчитанное для каждого такого эксперимента. Аналогично находится среднее значение выделившегося тепла:
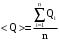 . (8)
. (8)Среднеквадратическая ошибка для скорости, 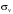 ,вычисляется по формуле:
,вычисляется по формуле:
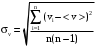 . (9)
. (9)Аналогично вычисляется среднеквадратическая ошибка
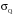 для количества выделившегося тепла:
для количества выделившегося тепла: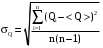 . (10)
. (10)Доверительный интервалы получим, умножив среднеквадратичную ошибку у (см. формулы (9) и (10))на коэффициент Стьюдента t:
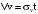 (11)
(11)
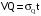 (12)
(12)
Коэффициент Стьюдента t зависит от числа измерений n и для надежности в = 90% имеет следующие значения: n | 2 | 3 | 4 | 5 | 6 |
t | 6,3 | 2,9 | 2,4 | 2,1 | 2 |
Окончательные результаты записываем в виде:
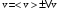 ,
,
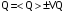 .
.
Здесь
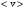 и
и  - числа, рассчитанные по формулам (7) и (8),
- числа, рассчитанные по формулам (7) и (8), 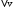 и
и 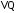 рассчитываем по формулам (11) и (12).
рассчитываем по формулам (11) и (12).#ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТы
Задание 1.
Цель задания 1: При постоянной массе маятника M изучить зависимость скорости пули v и работы деформации Q от массы пули m.
Порядок выполнения задания 1.
-
Загрузить файл «balmay.exe» -
Нажать клавишу «Enter», затем кнопку «Ручной режим», в этом режиме исходные параметры вводятся вручную:
масса маятника M – от 0,5 до 2 кг;
масса пули m – от 0,005 до 0,02 кг;
длина маятника l – от 1 до 3 м.
-
Нажать кнопку «Начать», затем ввести массу маятника M, массу пули m и длину маятника l в пределах указанных выше диапазонов. Записать эти параметры лабораторной установки в таблицу 1. -
Выполнить компьютерный эксперимент, для этого нажать кнопку «Старт», затем – «Снятие отсчёта». По появившейся линейке снять значения высоты подъёма маятника h, затем нажатием кнопки «Ok» убрать линейку. -
Выполнить компьютерный эксперимент с одинаковыми исходными параметрами не менее трёх раз. Результаты занести в таблицу 1. -
Изменить массу пули, повторить пункты 4 и 5 не менее трёх раз. -
Обработать результаты измерений,, используя формулу (5)–(12). (расчеты вести в системе СИ!) -
Проанализировать полученные результаты и сделать выводы.
Таблица 1.
