Файл: Курсовая работа Кинематический и силовой расчет механизма.rtf
Добавлен: 09.11.2023
Просмотров: 98
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Запишем уравнения, указанные в таблице, в развернутом виде.
-
Расстояние , определяющее точку приложения реакции
, определяющее точку приложения реакции  , найдем из уравнения моментов для звена 5:
, найдем из уравнения моментов для звена 5:
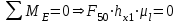 , откуда
, откуда 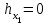 .
.В данном случае можно было заранее сказать, что плечо
 =0, так как все остальные силы, действующие на звено 5, проходят через центр шарнира
=0, так как все остальные силы, действующие на звено 5, проходят через центр шарнира  , следовательно, и реакция
, следовательно, и реакция  должна проходить через этот центр.
должна проходить через этот центр.-
Для определения реакции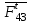 составляем уравнение моментов всех сил, действующих на звено 4, относительно точки
составляем уравнение моментов всех сил, действующих на звено 4, относительно точки  :
:
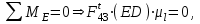 откуда
откуда 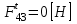 .
.В данном случае можно было заранее сказать, что реакция
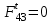 , так как все на звено 4 не действует никаких внешних нагрузок и, следовательно, реакция должна быть направлена вдоль звена.
, так как все на звено 4 не действует никаких внешних нагрузок и, следовательно, реакция должна быть направлена вдоль звена.-
Для определения нормальной составляющей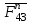 и реакции
и реакции  составляем уравнение статического равновесия сил, действующих на звенья 4 и 5:
составляем уравнение статического равновесия сил, действующих на звенья 4 и 5:
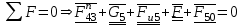
Силы, известные по величине и направлению, подчеркиваем двумя чертами, силы же, известные по направлению – одной чертой.
При составлении векторной суммы сил удобно силы, неизвестные по величине, писать в начале и в конце уравнения, чтобы при построении плана сил было проще пересечь их известные направления. Кроме того, при построении плана сил для всей группы рационально силы, относящиеся к одному звену, наносить последовательно друг за другом, т.е. группировать силы по звеньям, так как это упростит в дальнейшем определение реакции во внутренней кинематической паре.
Отрезки, изображающие известные силы на плане, определяем с учетом принятого масштабного коэффициента
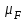 , который выберем по силе резания:
, который выберем по силе резания: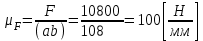 ,
,где
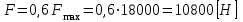 – сила сопротивления,
– сила сопротивления,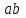 – отрезок в
– отрезок в 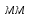 , изображающий эту силу на плане сил.
, изображающий эту силу на плане сил.Из произвольной точки в последовательности, указанной в уравнении, откладываем все известные векторы, начиная с
 . Далее через начало вектора
. Далее через начало вектора  проводим направление нормальной составляющей реакции
проводим направление нормальной составляющей реакции 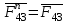 параллельно звену
параллельно звену  , а через конец вектора
, а через конец вектора  - направление реакции
- направление реакции  перпендикулярно оси
перпендикулярно оси  . Точка пересечения этих направлений определяет вектора, изображающие в выбранном масштабе реакции
. Точка пересечения этих направлений определяет вектора, изображающие в выбранном масштабе реакции  и
и  . Стрелки всех векторов должны соответствовать одному и тому же направлению обхода контура плана сил.
. Стрелки всех векторов должны соответствовать одному и тому же направлению обхода контура плана сил.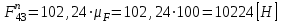 ;
;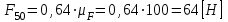 .
.Полная реакция
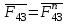 , т.е.
, т.е. 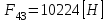 .
.-
-
Для определения реакции составляем уравнение равновесия сил для звена 4:
составляем уравнение равновесия сил для звена 4:
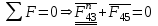 .
.Реакция
 неизвестна ни по величине, ни по направлению. Очевидно, что она равна по величине и противоположна по направлению реакции
неизвестна ни по величине, ни по направлению. Очевидно, что она равна по величине и противоположна по направлению реакции 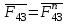 . Построение показано пунктиром.
. Построение показано пунктиром.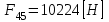
.
Реакция
 на звено 5 со стороны звена 4 равна по величине реакции
на звено 5 со стороны звена 4 равна по величине реакции  и противоположна ей по направлению.
и противоположна ей по направлению.Рассмотрев группу Ассура, состоящую из звеньев 4 и 5, переходим к следующей группе – 2ПГ 3 вида, состоящей из звеньев 2 и 3.
Рассматриваем группу 2-3: На данную структурную группу действуют следующие силы и моменты:
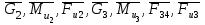 . Реакция
. Реакция 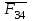 на звено 3 со стороны звена 4 равна по величине реакции
на звено 3 со стороны звена 4 равна по величине реакции  и противоположна ей по направлению
и противоположна ей по направлению 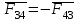 . Приложена эта реакция в точке
. Приложена эта реакция в точке  звена 3. Освободив группу 2-3 от связей, прикладываем вместо них две реакции
звена 3. Освободив группу 2-3 от связей, прикладываем вместо них две реакции 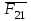 в шарнире
в шарнире  и
и 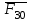 в шарнире
в шарнире  , неизвестные по величине и направлению.
, неизвестные по величине и направлению.Разложим реакцию
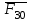 на две составляющие:
на две составляющие: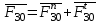
Нормальная составляющая действует вдоль звена 3:
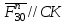 , тангенциальная составляющая действует перпендикулярно звену 3:
, тангенциальная составляющая действует перпендикулярно звену 3: 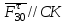 .
.Реакцию
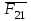 в шарнире
в шарнире  также разложим на составляющие:
также разложим на составляющие: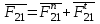 .
.Нормальная составляющая действует вдоль звена 2:
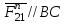 , тангенциальная составляющая действует перпендикулярно звену 2:
, тангенциальная составляющая действует перпендикулярно звену 2: 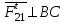 .
.Требуется также определить реакцию во внутренней кинематической паре
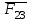 (или
(или 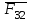 ). В 2ПГ 1 вида внутренняя кинематическая пара – вращательная.
). В 2ПГ 1 вида внутренняя кинематическая пара – вращательная.Для упорядочения расчетов по определению реакций составляем таблицу с указанием очередности определения сил, а также уравнений, посредством которых они будут определяться.
Таблица
| № п/п | Искомая величина | Вид уравнения | Звено, для которого составляется уравнение |
| 1 | | | 3 |
| 2 | | | 2 |
| 2 | | | 3, 2 |
| 3 | | | 2 (или 3) |
Запишем уравнения, указанные в таблице, в развернутом виде.
-
Для определения реакции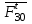 составляем уравнение моментов всех сил, действующих на звено 2, относительно точки
составляем уравнение моментов всех сил, действующих на звено 2, относительно точки  :
:
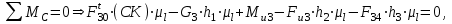 откуда
откуда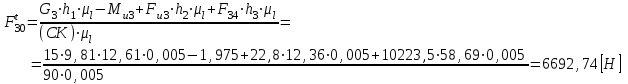
Знак "+" означает, что действительное направление силы соответствует первоначально выбранному.
-
Для определения реакции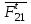 составляем уравнение моментов всех сил, действующих на звено 2, относительно точки
составляем уравнение моментов всех сил, действующих на звено 2, относительно точки  :
:
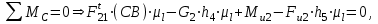 откуда
откуда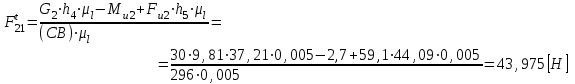
Знак "+" означает, что действительное направление силы соответствует первоначально выбранному.
-
Для определения нормальной составляющей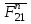 и реакции
и реакции 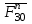 составляем уравнение статического равновесия сил, действующих на звенья 3 и 2:
составляем уравнение статического равновесия сил, действующих на звенья 3 и 2:
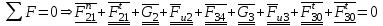
Силы, известные по величине и направлению, подчеркиваем двумя чертами, силы же, известные по направлению – одной чертой.
Отрезки, изображающие известные силы на плане, определяем с учетом ранее принятого масштабного коэффициента
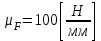 .
.Из произвольной точки в последовательности, указанной в уравнении, откладываем все известные векторы, начиная с
 . Далее через начало вектора
. Далее через начало вектора  проводим направление нормальной составляющей
проводим направление нормальной составляющей 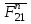 параллельно звену
параллельно звену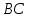 , а через конец вектора
, а через конец вектора  - направление реакции
- направление реакции 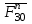 параллельно звену
параллельно звену 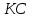 . Точка пересечения этих направлений определяет вектора, изображающие в выбранном масштабе реакции
. Точка пересечения этих направлений определяет вектора, изображающие в выбранном масштабе реакции 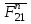 и
и 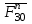 . Стрелки всех векторов должны соответствовать одному и тому же направлению обхода контура плана сил.
. Стрелки всех векторов должны соответствовать одному и тому же направлению обхода контура плана сил.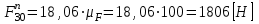 ;
;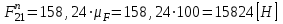 .
.Полную реакцию
 получим, соединив начало вектора
получим, соединив начало вектора 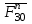 с концом вектора
с концом вектора  , а значение можно определить, пользуясь формулой:
, а значение можно определить, пользуясь формулой: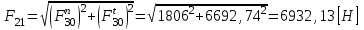 .
.Полную реакцию
 получим, соединив начало вектора
получим, соединив начало вектора 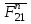 с концом вектора
с концом вектора  , а значение можно определить, пользуясь формулой:
, а значение можно определить, пользуясь формулой: