Файл: Курсовая работа Кинематический и силовой расчет механизма.rtf

Положение механизма
– вкт	5,60	2,80	0	0	0	58,81	2,35
– х.х.	2,21	1,11	20,46	1,16	0,05	39,05	1,56
– р.х.	3,05	1,52	19,63	1,07	0,04	17,82	0,71

Положение механизма
– вкт	128,79	5,15	1,40	7,32	2,61
– х.х.	39,51	1,58	1,74	1,66	1,74
– р.х.	75,01	3,00	0,75	3,95	0,79

---

5. 1   2   3   4

---

Кинетостатический расчет механизма

1. Определение сил инерции звеньев

Для рассматриваемого механизма чеканочного пресса заданы:

• 
  массы звеньев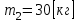 , 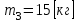и 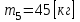(массы звеньев 1 и 4 не учитываются);
  
• 
  положения центров масс звеньев – координаты точек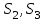 и ;
  
• 
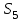  моменты инерци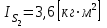и и .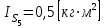
  

При определении сил инерции и моментов сил инерции воспользуемся построенным планом ускорений для нахождения ускорений центров масс звеньев и угловых ускорений звеньев для рабочего хода механизма:

• 
  ускорения центров масс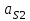 , 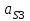и 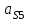возьмем из таблицы результатов:
  

, , .

• 
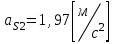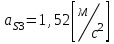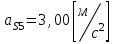  определение угловых ускорений звеньев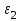 и 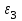также приведено при построении плана ускорений:
  

, .
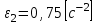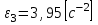Теперь рассчитаем модули сил инерции:

• 
  звено 2 совершает плоскопараллельное движение:
  

;

;

• 
  
  
• 
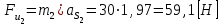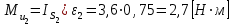  звено 3 вращательное движение:
  

;

;

• 
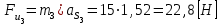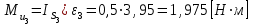  звено 5 совершает поступательное движение вдоль неподвижной направляющей:
  

.
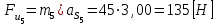Силы инерции

---

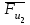
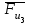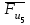, , приложены в центрах масс , 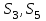звеньев и направлены противоположно соответствующим ускорениям 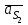, ,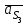 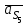. Моменты сил инерци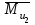и и 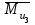по направлениям противоположены соответствующим угловым ускорениям 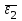и .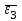

На схеме механизма в рассматриваемом рабочем положении показаны векторы сил инерции , , 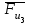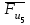и моменты сил инерции 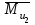, 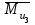. Здесь же штриховыми линиями показаны линейные ускорения центров масс 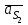, ,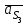 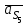и угловые ускорения 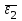и .

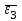2. Определение реакций в кинематических парах и уравновешивающей силы на кривошипе

Определение реакций в кинематических парах следует начинать с той группы Ассура, для которой известны все внешние силы. Такой группой является последняя присоединенная группа Ассура 2 вида, состоящая из звеньев 4, 5.

Рассматриваем группу 4-5. На данную структурную группу действуют следующие силы и моменты: 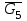, , 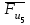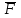. Действие отброшенных звеньев (стойки 0 и кулисы 3) заменяем реакциям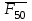и и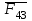

---

, которые необходимо определить.

Величина и точка приложения реакции в поступательной паре неизвестны, поэтому точка приложения этой реакции (расстояние 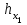) выбрано произвольно. Линия действия реакции без учета трения перпендикулярна направляющей этой пары. Реакция во вращательной паре неизвестна по величине и направлению. Без учета трения эта реакция проходит через центр шарнира. Разложим реакцию на две составляющие:

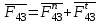
Нормальная составляющая действует вдоль звена 4: 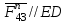, тангенциальная составляющая действует перпендикулярно звену 4: .

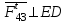Требуется также определить реакцию во внутренней вращательной кинематической паре группы 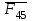(или 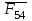), которая без учета трения проходит через центр шарнира . Для упорядочения расчетов по определению реакций составляем таблицу с указанием очередности определения сил, а также уравнений, посредством которых они будут определяться.
Таблица

№ п/п	Искомая величина	Вид уравнения	Звено, для которого составляется уравнение
1			5
2			4
3	,		4, 5
4	(или )		4 (или 5)

---